中科院1区SCI-哲学命题优化算法Philosophical proposition optimizer-附Matlab免费代码

1.简介

本文介绍了一种受哲学启发的优化算法，称为哲学命题优化器（ΦPO），它基于认识论中的哲学命题对知识获取进行建模。在所提出的哲学模型中，哲学命题的三种发展状态，正当化的真实信念（JTB）、可能错误的信念（PFB）和不合理的真实信念（UTB），使用三种专门的运算符迭代提炼：提供正当化（PJ）、提高形而上学怀疑主义（RMS）和提高认知怀疑主义（RES）。

为了评估ΦPO在具有挑战性的优化问题上的性能，将其应用于IEEE 2014年和2024年进化计算大会（CEC 2014年和2024年）的单目标界约束基准问题，以及对工程问题进行基准测试。将ΦPO的性能与五类算法进行比较：（1）广泛使用的经典方法，（2）已建立的2019年后方法，（3）先进的基于PSO和DE的方法，（4）CEC竞赛的获胜者。

2 哲学命题优化器（ΦPO）

2.1 灵感、动机与方法论

哲学一词源于希腊语"Philosophia"，由毕达哥拉斯创造，意为"对智慧的热爱"。哲学是对人类在世界与生命中所面临的最根本、最核心问题的思考；它研究关于存在、知识、价值、理性与心灵的一般性问题，作为待研究或待解决的课题。换言之，哲学是一门科学，使人类能够从更高、更广阔的视角审视对象、事件与事务（Law 2007；Honderich et al. 1996）。本小节阐述启发PO算法发展的哲学概念与定义。

认识论是哲学的一个分支，关注人类知识及其本质、界限与其他相关问题。它来自希腊词"episteme"（意为知识、理解或熟识）与"logos"（意为说明、论证、理由或话语）（Steup 与 Ram 2020；Simpson et al. 2014；Stroll 与 Martinich 2021）。据 Steup 与 Ram 2020，知识可三元分析如下：主体 S 知道命题 p 当且仅当：

(1) p 为真；

(2) S 相信 p；且

(3) S 有理由相信 p。

因此，经证成的真信念（本研究缩写为JTB）被视为知识的必要且充分条件。

希腊词"skepsis"意为"探究"。怀疑论观点考虑信念可能为假的情形（Nozick 1983）。哲学怀疑论有多种类型、形式与程度；例如，一些激进怀疑论者否认某类一般知识的可能性，而另一些则声称对某些知识无确定性。本文采纳后者。据 Speaks（Speaks 2007），在信念领域内，对任何给定哲学命题可区分两种怀疑视角：形而上学怀疑论者断言所涉信念为假，而认识论怀疑论者不否认其真，但主张其未获证成。基于这一分析方法，我们在此提出一个关于哲学命题（PPs）怀疑与证成过程的模型，包含如下三种不同状态：

1. 经证成的真信念（JTB）
2. 未经证成的真信念（UTB）
3. 可能为假的信念（PFB）

该模型以图1图形化表示。一般而言，回应针对某信念的怀疑可证成该命题，使其被承认为知识。批判性思维作为一切智力发展的主要成分，使我们能够应对哲学命题面临的挑战并为之提供证成。另一方面，思维过程也可能通过提出新问题对命题产生进一步怀疑。因此，提供证成与提出新问题充当哲学算子，将初始信念转化为经证成的真信念（JTBs），即知识。

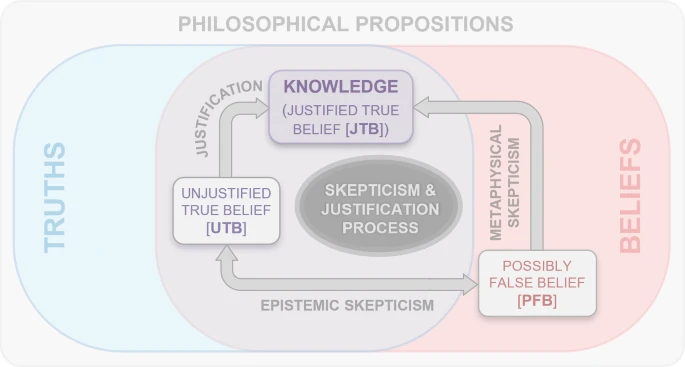
图1 哲学命题的怀疑和论证过程模型，说明如何检查信念并将其转化为知识

基于此讨论，我们定义了三个根据命题行事的运算符如下：

1.提供理由（PJ）

2.提高认识怀疑主义（RES）

3.提高形而上学怀疑论（RMS）

辩解和怀疑主义的两种形式构成了提炼哲学命题的工具包。在给定的哲学领域内反复的质疑和辩解循环推动了它的发展。这种反复的沉思过程产生了越来越稳健的答案，类似于优化的迭代性质。由于每个沉思状态都可能包含隐藏的缺陷，因此其结论的有效性仍然是暂时的。也就是说，由于潜在的沉思状态的潜在缺陷，新答案的可靠性是不确定的。哲学家批判性地检查这些试探性的结论，找出论点中的弱点（法律2007），然后寻找新的命题来解决这些缺陷。每个辩解和怀疑的循环都会产生新的理由，这些理由反过来又成为进一步探究的主题。

在经典认识论中，正当化真实信念（JTB）通常被视为知识的充分条件，而怀疑主义通常以正当化为目标，而不会在状态之间转换信念。然而，在发展ΦPO时，我们有意采用动态、迭代的知识评估观点。我们不将JTB、UTB和PFB视为固定类别，而是将其视为发展状态，使用正当化和怀疑作为提炼候选解的机制。

在这个框架内，证明和怀疑不会否定知识，而是引入批判性的询问来揭露解决方案中隐藏的缺陷或被忽视的方面，从而促使重新评估。在这个模型中，提供证明（PJ）运算符使用UTB修改JTB，而提高形而上学怀疑主义（RMS）运算符根据较弱的命题（如PFB）调整JTB。最后，提高认知怀疑主义（RES）运算符模型对UTB和PFB的怀疑，解决这些真假信念的影响。

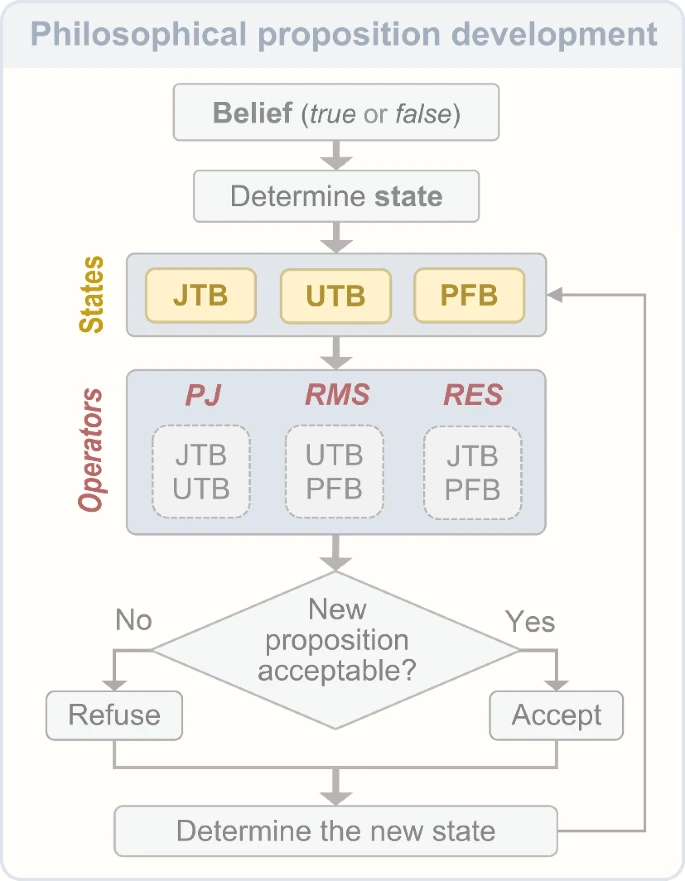
图2 哲学命题的发展过程

图2所示的过程描述了ΦPO的迭代改进：对最优解的搜索是动态的，而不是线性的，强调了任何关于最优性的信念的临时性质和重复测试的必要性。

3.2 数学模型

本节基于前一节提出的命题与算子，描述PO算法的数学模型。值得注意的是，当前PO公式专为连续数值优化问题设计；若涉及名义变量且缺乏边界与距离概念，算子可能失效。算法中，每个潜在解被视为一个哲学命题（PP），可含多个属性（即维度）。此处假设所有PP维度相同，记为 d d d，由问题决策变量数决定。于是，哲学命题可视为 d d d维空间中的点，用矩阵表示为

P P = [ P P 1 P P 2 ⋮ P P n ] = [ p p 11 p p 12 ⋯ p p 1 d p p 21 p p 22 ⋯ p p 2 d ⋮ ⋮ ⋱ ⋮ p p n 1 p p n 2 ⋯ p p n d ] (1) \mathrm{PP}= \begin{bmatrix} \mathrm{PP}1\\[2mm] \mathrm{PP}2\\[2mm] \vdots\\[2mm] \mathrm{PP}n \end{bmatrix} =\begin{bmatrix} pp{11} & pp{12} & \cdots & pp{1d}\\[2mm] pp_{21} & pp_{22} & \cdots & pp_{2d}\\[2mm] \vdots & \vdots & \ddots & \vdots\\[2mm] pp_{n1} & pp_{n2} & \cdots & pp_{nd} \end{bmatrix} \tag{1} PP= PP1PP2⋮PPn = pp11pp21⋮ppn1pp12pp22⋮ppn2⋯⋯⋱⋯pp1dpp2d⋮ppnd (1)

其中 d d d为设计变量数， n n n为PP数量， P P i \mathrm{PP}i PPi为第 i i i个哲学命题。每个分量 p p i j pp{ij} ppij在其定义边界内随机初始化。虽可在初始阶段采用更高级技术，但引入此类方法将直接影响算法性能，使与其他方法的公平对比变得困难。然而，设计良好的初始化阶段常对优化方法贡献显著；若证明有效，可替代其他算法中的传统初始化，从而提升其性能。

初始化PP后，按适应度值将所有PP划分为"更优"与"更差"两组。为保持算法简洁，适应度值直接来自目标函数，最小化问题中值越小越优。随后，为每个PP定义三种状态：

1. JTB：当前命题 P P i \mathrm{PP}_i PPi视为JTB；
2. UTB：从最优PP（即"更优"组+JTB）中随机另选一命题 P P j \mathrm{PP}_j PPj作为UTB，引入对当前JTB的怀疑；
3. PFB：再从"更差"组随机选一与UTB质量"相距较远"的命题 P P k \mathrm{PP}_k PPk作为PFB。

虽存在替代策略选择UTB与PFB，但我们采用此直接方式，确保JTB+UTB+PFB满足上述规则。确定命题状态后，依据图2所示概念应用对应算子进行修改。算子如下：

1. 提供证成（PJ）： U T B − J T B \mathrm{UTB}-\mathrm{JTB} UTB−JTB，用于基于UTB修改JTB；
2. 引发认识怀疑（RES）： P F B − J T B \mathrm{PFB}-\mathrm{JTB} PFB−JTB，用于基于PFB修改JTB；
3. 引发形而上学怀疑（RMS）： P F B − U T B \mathrm{PFB}-\mathrm{UTB} PFB−UTB，用于基于PFB修改UTB。

简言之，PJ算子用UTB修正JTB，RES算子用PFB修正JTB，RMS算子在PFB与UTB定义的空间内引入怀疑，将较劣命题导向较优命题。为简洁，将这三个哲学命题发展算子线性合并，用单一方程表示：

P P i , new = S 1 + r 1   b 1   ( S 2 − S 1 ) + r 2   b 2   ( S 3 − S 1 ) + r 3   b 3   ( S 3 − S 2 ) (2) \mathrm{PP}_{i,\text{new}} = \mathrm{S}_1 + r_1\,b_1\,(\mathrm{S}_2-\mathrm{S}_1) + r_2\,b_2\,(\mathrm{S}_3-\mathrm{S}_1) + r_3\,b_3\,(\mathrm{S}_3-\mathrm{S}_2) \tag{2} PPi,new=S1+r1b1(S2−S1)+r2b2(S3−S1)+r3b3(S3−S2)(2)

其中 r 1 , r 2 , r 3 r_1,r_2,r_3 r1,r2,r3为区间 [ 0 , 1 ] [0,1] [0,1]的随机向量； S \mathrm{S} S为状态向量，其元素由JTB( i i i)、UTB( j j j)、PFB( k k k)构成； b 1 , b 2 b_1,b_2 b1,b2为取0或1的随机整数； b 3 = s i g n ( f S 2 − f S 3 ) b_3=\mathrm{sign}(f_{\mathrm{S}2}-f{\mathrm{S}3}) b3=sign(fS2−fS3)， f S 2 , f S 3 f{\mathrm{S}2},f{\mathrm{S}_3} fS2,fS3分别为对应PP的目标函数值。系数 b 1 , b 2 , b 3 b_1,b_2,b_3 b1,b2,b3称平衡因子。

尽管式(2)在结构上似与某些算法（如DE）的线性组合方案相似，其设计在概念上迥异：它由认识论推理驱动，而非数值启发式。方程中每一项对应特定类型的哲学命题，通过二元开关( b 1 , b 2 b_1,b_2 b1,b2)与基于适应度的符号逻辑门( b 3 b_3 b3)选择性激活。该表述将基于推理的动力学嵌入搜索过程，无需传统控制参数（如变异或交叉率）。因此，算法通过认识建模而非参数调节获得自适应行为，在理论与实践中均具区别性。

值得注意的是，若 b 3 b_3 b3亦按二元处理，可能出现所有项为零、导致不生成新解的情形。为避免此，我们将 b 3 b_3 b3设为符号函数，取值仅 − 1 -1 −1或 + 1 +1 +1，而非二元变量，并作为方程主成分。这确保方程始终含活跃分量驱动解的演化。特别地，当 S 2 \mathrm{S}_2 S2选自"更优"组（UTB）、 S 3 \mathrm{S}_3 S3选自"更差"组（PFB）时， b 3 = 1 b_3=1 b3=1，可省略不写。同时， b 1 , b 2 b_1,b_2 b1,b2作为二元开关，依据平衡参数调节对应项影响。该结构保持方程灵活性，在优化过程中同时支持主动细化与自适应平衡。

新解生成依赖JTB( i i i)、UTB( j j j)、PFB( k k k)的排列。此过程可用状态向量 S \mathrm{S} S建模，决定式(2)中 S 1 , S 2 , S 3 \mathrm{S}_1,\mathrm{S}_2,\mathrm{S}_3 S1,S2,S3的JTB、UTB、PFB排列。本研究考虑三种可能状态向量： [ i , j , k ] [i,j,k] [i,j,k]、 [ j , k , i ] [j,k,i] [j,k,i]、 [ k , i , j ] [k,i,j] [k,i,j]。为保持算法动态性，每次迭代对每个PP随机选取其一应用。即，每次迭代中，每个PP随机选一状态（JTB、UTB或PFB）作为主状态( S 1 \mathrm{S}_1 S1)，随后所有定义算子均作用于该状态。

若新解超出边界，PO算法采用下式将违规变量替换为边界值：

p p i j , new = { min ⁡ ( p p i j , ub ,   p p i j , new ) , 若 p p i j , new < p p i j , lb max ⁡ ( p p i j , lb ,   p p i j , new ) , 若 p p i j , new > p p i j , ub (3) pp_{ij,\text{new}}= \begin{cases} \min(pp_{ij,\text{ub}},\,pp_{ij,\text{new}}),& \text{若 }pp_{ij,\text{new}}<pp_{ij,\text{lb}}\\[2mm] \max(pp_{ij,\text{lb}},\,pp_{ij,\text{new}}),& \text{若 }pp_{ij,\text{new}}>pp_{ij,\text{ub}} \end{cases} \tag{3} ppij,new=⎩ ⎨ ⎧min(ppij,ub,ppij,new),max(ppij,lb,ppij,new),若 ppij,new<ppij,lb若 ppij,new>ppij,ub(3)

其中 p p i j , new pp_{ij,\text{new}} ppij,new为第 i i i个新解（ P P i , new \mathrm{PP}{i,\text{new}} PPi,new）的第 j j j个设计变量， min ⁡ ( ⋅ ) \min(\cdot) min(⋅)与 max ⁡ ( ⋅ ) \max(\cdot) max(⋅)分别返回 p p i j , ub pp{ij,\text{ub}} ppij,ub与 p p i j , lb pp_{ij,\text{lb}} ppij,lb的极小、极大值。检查 P P i , new \mathrm{PP}{i,\text{new}} PPi,new边界违规后，计算其目标函数值 f i , new f{i,\text{new}} fi,new，并与 f i f_i fi比较以确定更优位置：

P P i = { P P i , 若 f ( P P i ) 优于 f ( P P i , new ) P P i , new , 若 f ( P P i , new ) 优于 f ( P P i ) (4) \mathrm{PP}i= \begin{cases} \mathrm{PP}i,& \text{若 }f(\mathrm{PP}i)\text{优于}f(\mathrm{PP}{i,\text{new}})\\[2mm] \mathrm{PP}{i,\text{new}},& \text{若 }f(\mathrm{PP}{i,\text{new}})\text{优于}f(\mathrm{PP}_i) \end{cases} \tag{4} PPi=⎩ ⎨ ⎧PPi,PPi,new,若 f(PPi)优于f(PPi,new)若 f(PPi,new)优于f(PPi)(4)

算法终止准则为达到最大迭代次数，此时优化过程结束。

综上，PO算法实现流程分六步：

• 步骤1：定义参数，包括哲学命题数( N pop N_{\text{pop}} Npop)、最大迭代数( MaxIter \text{MaxIter} MaxIter)及其他问题特定设置；
• 步骤2：随机生成初始解并计算对应目标函数值；
• 步骤3：按适应度值划分"更优"与"更差"两组，将每个PP归入其一；
• 步骤4：对每个第 i i i个PP重复以下子步骤：
  • 步骤4.1：确定JTB、UTB、PFB；
  • 步骤4.2：随机生成索引向量 S \mathrm{S} S（JTB、UTB、PFB的排列）；
  • 步骤4.3：用式(2)生成新 P P i \mathrm{PP}_i PPi，并用式(3)进行边界控制；
  • 步骤4.4：按式(4)评估并更新新 P P i \mathrm{PP}_i PPi；
• 步骤5：检查终止准则；若未满足，从步骤3重复。

PO算法流程图见图3。以下各小节给出每种选定状态的详细方程，它们均由式(2)一般形式导出的特定情形。

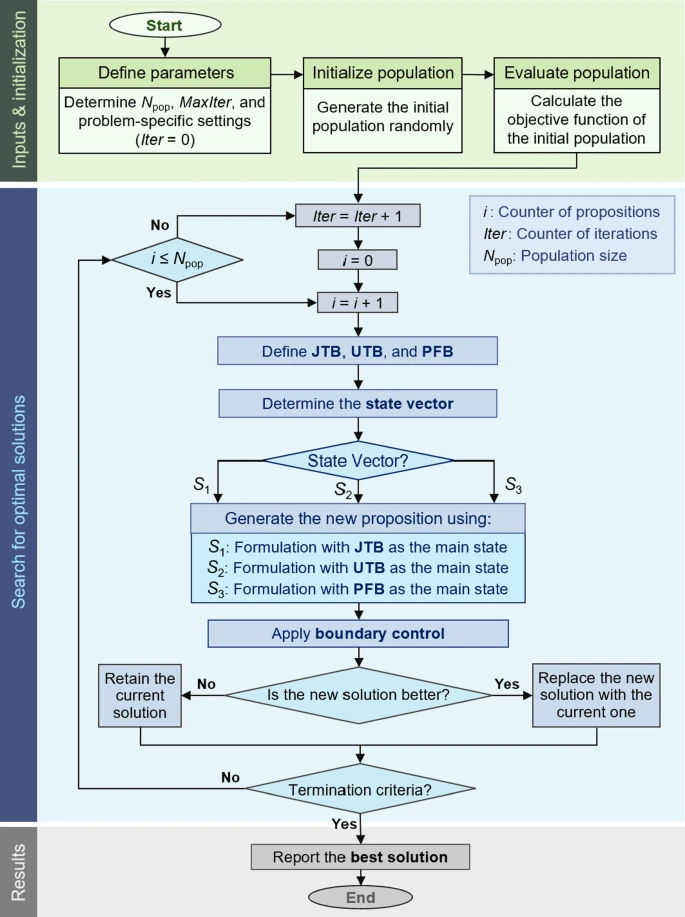
图3 流程国

3.2.1 以 JTB 为主状态的表述

作为第一种选择，主命题为 JTB（即 JTB = PP i _i i），状态向量设为 S = [ i , j , k ] S=[i,j,k] S=[i,j,k]。此时因 S 1 = i S_1=i S1=i，移动从 PP i _i i 开始。

令 S 1 = i ,    S 2 = j ,    S 3 = k S_1=i,\;S_2=j,\;S_3=k S1=i,S2=j,S3=k，式 (2) 可重写为

PP new = PP i + r 1 b 1 ( PP j − PP i ) + r 2 b 2 ( PP k − PP i ) + r 3 b 3 ( PP k − PP j ) (5) \text{PP}_{\text{new}} = \text{PP}_i + r_1b_1(\text{PP}_j-\text{PP}_i) + r_2b_2(\text{PP}_k-\text{PP}_i) + r_3b_3(\text{PP}_k-\text{PP}_j) \tag{5} PPnew=PPi+r1b1(PPj−PPi)+r2b2(PPk−PPi)+r3b3(PPk−PPj)(5)

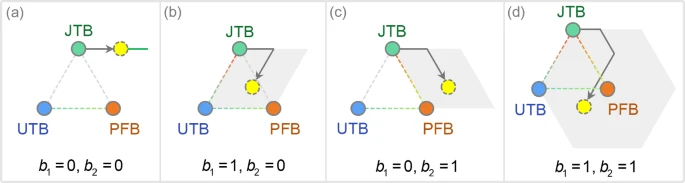
按此表述，变化从 PP i _i i（=JTB）出发，三种定义算子的组合决定新命题。平衡因子的效果见图 4。

若 b 1 = b 2 = 0 b_1=b_2=0 b1=b2=0，则新 PP 通过 RMS 改变 JTB 获得。此时 b 3 = 1 b_3=1 b3=1 恒保证新解将沿其他命题方向被修正，而 JTB 本身不影响方向（图 a）。

若 b 1 = 1 b_1=1 b1=1 且 b 2 = 0 b_2=0 b2=0，新 PP 基于 PJ 与 RMS 生成（图 b）。

若 b 1 = 0 b_1=0 b1=0 且 b 2 = 1 b_2=1 b2=1，则使用 RES 与 RMS（图 c）。

最后，若 b 1 = b 2 = 1 b_1=b_2=1 b1=b2=1，所有算子共同生成新 PP（图 d）。

3.2.2 以 UTB 为主状态的表述

此时主命题为 UTB，故变化从 PP j _j j 开始，该位置即为 UTB 原点。

该状态对应 S = [ j , k , i ] S=[j,k,i] S=[j,k,i]，即 S 1 = j ,    S 2 = k ,    S 3 = i S_1=j,\;S_2=k,\;S_3=i S1=j,S2=k,S3=i；于是式 (2) 可重写为

PP new = PP j + r 1 b 1 ( PP k − PP j ) + r 2 b 2 ( PP i − PP j ) + r 3 b 3 ( PP i − PP k ) (6) \text{PP}_{\text{new}} = \text{PP}_j + r_1b_1(\text{PP}_k-\text{PP}_j) + r_2b_2(\text{PP}_i-\text{PP}_j) + r_3b_3(\text{PP}_i-\text{PP}_k) \tag{6} PPnew=PPj+r1b1(PPk−PPj)+r2b2(PPi−PPj)+r3b3(PPi−PPk)(6)

其中 b 3 = sign ( f k − f i ) b_3=\text{sign}(f_k-f_i) b3=sign(fk−fi)。

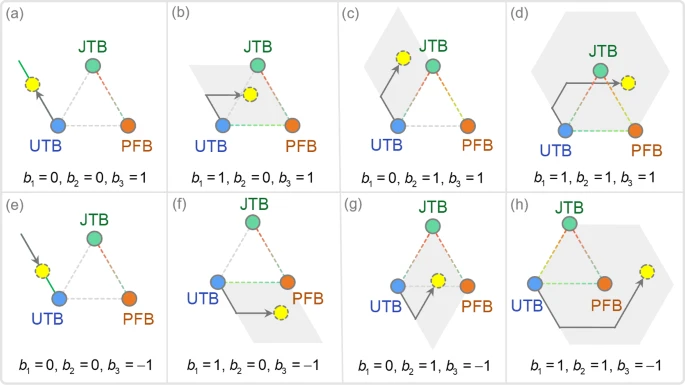
图 5 展示了平衡因子对该修改搜索过程的影响。

3.2.3 以 PFB 为主状态的表述

最后一种情况，主命题为 PFB（PP k _k k）。因此修改从 PP k _k k 开始，该表述使用 S = [ k , j , i ] S=[k,j,i] S=[k,j,i]，即 S 1 = k ,    S 2 = j ,    S 3 = i S_1=k,\;S_2=j,\;S_3=i S1=k,S2=j,S3=i。于是第三方程为

PP new = PP k + r 1 b 1 ( PP j − PP k ) + r 2 b 2 ( PP i − PP k ) + r 3 b 3 ( PP i − PP j ) (7) \text{PP}_{\text{new}} = \text{PP}_k + r_1b_1(\text{PP}_j-\text{PP}_k) + r_2b_2(\text{PP}_i-\text{PP}_k) + r_3b_3(\text{PP}_i-\text{PP}_j) \tag{7} PPnew=PPk+r1b1(PPj−PPk)+r2b2(PPi−PPk)+r3b3(PPi−PPj)(7)

其中 b 3 = sign ( f j − f i ) b_3=\text{sign}(f_j-f_i) b3=sign(fj−fi)。图 6 给出了对应此状态的过程示意。

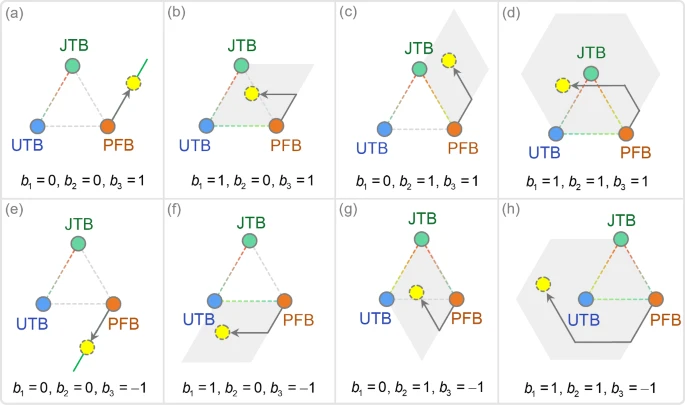
需注意，式 (5)、(6)、(7) 均源自式 (2) 的一般形式，每次仅通过内部逻辑开关 ( b 1 , b 2 , b 3 ) (b_1,b_2,b_3) (b1,b2,b3) 激活其中之一，这些开关在所有方程中共享，并非独立参数。

4.完整代码

%Main code for 
% Philosophy Optimizer (PhO)
% Journal: Artificial Intelligence Review (2025)
% Authors: S. TalatAhari, H. Bayzidi, P. Sareh

function Output=PHO(nDim,MaxIter,nPop)

Convergence = zeros(MaxIter,1);

% Problem Information
[LB, UB] = ProbInfo;
LB = LB.*ones(1,nDim);
UB = UB.*ones(1,nDim);

%% Initialization
X = nan(nPop,nDim);
Obj = nan(nPop, 1);

for i = 1:nPop
    X(i,:) = LB + rand(1,nDim).*(UB - LB);
    Obj(i) = Objective(X(i,:));
end

%% PhO Main Loop
for Iter = 1:MaxIter
    for i = 1:nPop
        % Philisopical Selection
        [~,idsorted]=sort(Obj);
        idsorted(idsorted==i)=[];
        jkid=randperm(fix((nPop-1)/2),2)+ [0,fix((nPop-1)/2)];
        jk=idsorted(jkid)';
        
        % Philosophical State
        m = [i jk];
        m = m(randperm(3));
        
        % r1,r2,r3,s1,s2,s3
        r1=rand(1,nDim);
        r2=rand(1,nDim);
        r3=rand(1,nDim);
        s1=randi([0,1]);
        s2=randi([0,1]);
        s3=sign(Obj(m(2))-Obj(m(3)));
        
        % New Solution Gereation
        NewX = X(m(1),:)...
            + s1.*r1.*(X(m(2),:)-X(m(1),:)) ...
            + s2.*r2.*(X(m(3),:)-X(m(1),:)) ...
            + s3.*r3.*(X(m(3),:)-X(m(2),:));
        
        % Clamp New Solution
        NewX = min(max(NewX,LB),UB);
         
        % Evaluation
        NewObj =  Objective(NewX);
      
        if NewObj <= Obj(i)
            Obj(i) = NewObj;
            X(i, :) = NewX;
        end
    end
    
    % Find The Best Theory
        [ObjBest,bestid] = min(Obj);    
       

    % Dispaly Result In Each Iteration
    disp([' Iter: ' num2str(Iter) ' fmin = ' num2str(ObjBest)])
    
    Convergence(Iter)=ObjBest;
end
Output.ObjBest=ObjBest;
Output.Conve=Convergence;
end
%% addational functions
function obj=Objective(X)
    obj=sum(X.^2);
end

function [LB,UB]=ProbInfo
    LB=-5;
    UB=+5;
end

Talatahari, S., Bayazidi, H. & Sareh, P. Philosophical proposition optimizer (ΦPO): an epistemology-inspired algorithm for numerical optimization. Artif Intell Rev 58, 405 (2025). https://doi.org/10.1007/s10462-025-11383-8.