【科研学习记录】自适应动态规划（ADP）与强化学习（RL）理论入门

前言

本文为本人参加科研小组相关理论的学习笔记，主要供本人学习、复习，不是教学或经验分享，若有错误，请大佬轻喷。

前置说明：核心思想统一

DP、ADP、RL所解决的核心问题是一致的：一个可交互的动态系统，通过一系列的"动作"，让系统从当前"状态"出发，最终获得累计"回报"的最大值

三者的核心思想高度统一：将复杂的多步决策问题拆分为多个简单的单步决策问题，利用"贝尔曼方程"实现决策的递推优化，最终找到全局最优"策略"

三者的本质区别 仅在于：是否依赖系统的精确模型（状态转移 + 回报函数） 、从何处获取数据 、如何逼近最优解。

记住 3 个最核心的基础概念，后续全程围绕它们展开：

1. 状态（State, s）：系统当前的 "情况"，是决策的依据（比如：机器人的位置 / 速度、游戏的当前画面、迷宫中玩家的坐标）；
2. 动作（Action, a）：智能体 / 控制器对系统做出的 "选择"（比如：机器人前进 / 左转、游戏中向上 / 开枪、迷宫中走东 / 南）；
3. 回报（Reward, r）：系统在状态s下做动作a后，得到的 "即时反馈"（比如：机器人走到目标点得 + 10 分、撞到墙得 - 5 分，游戏中击杀敌人得 + 50 分，迷宫中走出迷宫得 + 100 分）。

一、数学基础：3 个核心知识点（极简版）

提前铺垫 3 个最关键的数学概念，后续推导会直接用到，仅讲核心用途，不做抽象证明，初学者无需深入钻研，知道 "是什么、怎么用" 即可：

1. 期望（Expectation, E）

通俗解释 ：随机事件所有可能结果的 "加权平均值"，权重是结果发生的概率。用途 ：DP/ADP/RL 中，状态转移和回报往往是随机的（比如机器人行动可能因噪音偏移），用期望表示 "平均意义上的回报 / 状态转移"。公式：若随机变量X的可能取值为x1​,x2​,...,xn​，概率为p1​,p2​,...,pn​，则E[X]=∑i=1n​pi​xi​。

2. 递推关系

通俗解释 ：一个问题的解可以由 "更小的同类问题的解" 推导而来（比如：第 n 项的值由第 n-1 项推导）。用途 ：DP/ADP/RL 的核心是 "多步决策的递推优化"，贝尔曼方程的本质就是回报的递推关系。

3. 压缩映射（Contraction Mapping）

通俗解释 ：对一个函数反复做 "映射"，最终会收敛到一个唯一的不动点 （比如：把一张纸反复按固定规则折叠，最终会缩到一个点）。用途 ：证明 DP/ADP/RL 的迭代算法一定会收敛到最优解（初学者先记住结论：贝尔曼算子是压缩映射，因此迭代会收敛）。

二、极简动态规划（DP）

DP 是解决多阶段序贯决策优化 的经典方法，ADP 是自适应化的 DP ，RL 是试错式的无模型 DP ，三者共享马尔可夫决策过程（MDP）框架 和贝尔曼方程，这是唯一需要掌握的 DP 核心，其余细节无需深究。

1. DP 的核心问题

在动态交互系统 中，智能体 / 控制器通过选择一系列动作 ，让系统从当前状态 出发，使累计折扣回报 的期望最大化，最终得到全局最优策略。

2. 必记：MDP 五要素（<S,A,P,R,γ>）

所有 ADP/RL 问题都基于 MDP 建模，这是符号基础，后续全程沿用，务必记牢：

要素	符号	通俗解释	核心作用
状态空间	S	系统 / 环境的所有可能 "情况"（如机器人位置、游戏画面）	决策的唯一依据（无后效性）
动作空间	A	智能体可执行的所有 "选择"（如机器人前进、游戏开枪）	智能体改变状态的手段
状态转移概率	P	Pss′a​=P(st+1​=s′∣st​=s,at​=a)	状态s做动作a到s′的概率（模型核心）
即时回报函数	R	Rss′a​=r(s,a,s′)	状态转移后得到的即时反馈（奖励 / 惩罚）
折扣因子	γ	0≤γ<1	折现未来回报，保证累计回报有限、收敛

关键备注：γ越接近 1，越重视未来回报；γ=0仅关注即时回报。

3. 必记：贝尔曼最优方程（ADP/RL 的数学灵魂）

DP/ADP/RL 的所有算法，本质都是迭代求解贝尔曼最优方程 ，其是价值函数的递推关系，核心是 **"当前价值 = 即时回报 + 折扣后的未来最优价值"**，两个核心形式（后续 ADP/RL 全围绕此展开）：

（1）状态价值函数版 V∗(s)

V∗(s)表示状态s的最大价值 （从s出发的最优累计回报期望）：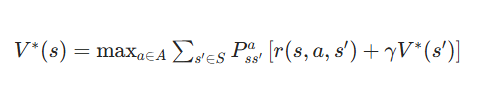

V∗​(s)：状态价值函数详解 ------"这个位置好不好？"

1. 符号全翻译（机器人场景版）

符号	大白话意思（机器人）
V∗​(s)	状态 s 的最优总价值（核心结果）
s	机器人当前的位置 / 状态（比如坐标 (1,2)）
maxa∈A​	从所有能做的动作里挑最好的那个（前进 / 左转 / 右转）
∑s′∈S​	把所有可能走到的下一个位置的结果加起来（因为有概率）
Pss′a​	机器人在 s 位置做 a 动作，走到下一个位置 s' 的概率
r(s,a,s′)	从 s 做 a 到 s'，当下拿到的即时奖励 / 惩罚
γV∗​(s′)	下一个位置 s' 的最优价值，打个折（未来的价值）

2. 公式的核心意义

V∗​(s)算的是：机器人现在站在 s 这个位置，从这开始往后选「最优的走法」，最终能拿到的「总奖励平均值」（因为有概率 P）。 简单说就是：这个位置是 "风水宝地" 还是 "坑"------ 数值越大，说明从这个位置出发，后续能拿的总奖励越多，位置越好。

3. 机器人场景的极简逻辑

比如机器人在位置 s1，能做 "前进""左转" 2 个动作：

• 选 "前进"：80% 走到 s2（奖励 + 10）、20% 撞墙 s0（奖励 - 50），s2 的最优价值 V*(s2)=50，s0 的最优价值 V*(s0)=-100；
• 选 "左转"：100% 走到 s3（奖励 0），s3 的最优价值 V*(s3)=30；V∗(s1)就是从这两个动作里挑一个，算出该动作的「即时奖励 + 折扣未来价值」的概率平均值，取最大的那个数------ 这就是 s1 位置的 "最优价值"。

（2）动作价值函数版 Q∗(s,a)

Q∗(s,a)表示状态s选动作a的最大价值 （更常用，无需P）：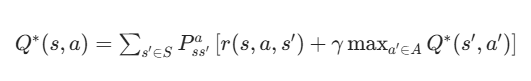

Q∗​(s,a)：动作价值函数 ------"在这个位置，做这个动作好不好？"

这是最实用的公式（无模型 RL/ADP 全用它），比V∗​(s)更 "具体"，也是后续找最优走法的核心。

1. 符号全翻译（机器人场景版）

和V∗​(s)几乎一样，唯一区别 ：没有最外层的maxa∈A​，因为Q∗​(s,a)已经绑定了具体动作 a。

新增 / 变化符号	大白话意思（机器人）
Q∗​(s,a)	机器人在 s 位置做 a 动作的最优总价值（核心结果）
maxa′∈A​	走到下一个位置 s' 后，再选最好的动作 a'（后续依然最优）

2. 公式的核心意义

Q∗​(s,a)算的是：机器人现在站在 s 位置，「确定做 a 这个具体动作」，从这一步开始往后继续选最优走法，最终能拿到的「总奖励平均值」。 简单说就是：在这个位置，选这个动作划不划算------ 数值越大，说明这个动作的性价比越高，越值得做。

3. 和V∗​(s)的关键区别（小白必懂）

• V∗(s)：只评位置（这个地方好不好），背后隐含了 "会选最优动作"；
• Q∗(s,a)：评 "位置 + 具体动作"（在这地方做这个动作好不好），更直接、更落地。

关联关系 ：一个位置的最优价值V∗​(s)，就是这个位置所有动作里Q 值最大的那个（V∗​(s)=maxa​Q∗​(s,a)），相当于V∗​(s)是Q∗​(s,a)的 "浓缩版"。

为什么 RL/ADP 都用 Q？因为实际中我们要的不是 "位置好不好"，而是 "在这个位置该做什么动作"，Q 直接绑定动作，不用再额外推导。

核心结论 ：求出V∗/Q∗后，通过贪心策略 即可得到最优策略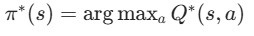：（动作价值版更直接，无模型 ADP/RL 均用此）。

4. 传统 DP 的 3 个致命局限（ADP/RL 的诞生原因）

这是理解 ADP 和 RL 的关键前提------ 正因为传统 DP 无法解决实际问题，才诞生了 ADP（控制工程视角）和 RL（人工智能视角）的解决方案：

1. 模型依赖 ：必须知道精确的P和R，但现实中系统 / 环境模型大多未知 / 难以精确建模（如机器人摩擦、交通环境）；
2. 维度灾难 ：表格型表示价值函数，高维 / 连续状态 / 动作空间下，表格规模指数级爆炸（如机器人位置 + 速度，维度稍高就无法存储）；
3. 离线计算 ：需提前完成所有迭代，无法适应时变系统（如机器人负载变化、环境参数改变）。

三、自适应动态规划（ADP）------ 控制工程视角的 DP 进化版

ADP 由 Werbos 在 1970 年代提出，是控制工程领域 为解决传统 DP 局限而生的方法，核心定位是：基于数据的、在线自适应的、带函数逼近的无模型 / 半模型 DP ，首要要求是闭环系统的稳定性（控制工程核心诉求，如机器人、倒立摆不能失控）。

1. ADP 的核心改进（直击 DP 的 3 个局限）

ADP 对传统 DP 的改进是本质性的，也是其能应用于实际控制问题的关键：

DP 的局限	ADP 的解决方案	核心原理
模型依赖（需P/R）	数据驱动代替模型驱动	无需已知P/R，通过智能体与系统的在线交互数据(s,a,r,s′)，直接估计价值函数，用实际数据代替模型计算
维度灾难（表格型）	函数逼近代替表格型	用函数逼近器（FA）（神经网络 / 线性回归 / 模糊系统）表示价值函数 / 策略，将高维状态映射为低维参数，如V^(s;θ)（θ为参数）
离线计算（无法时变）	在线自适应迭代	与系统实时交互、实时更新参数，策略随系统 / 环境变化动态调整，适应时变系统

2. ADP 的标志性核心组件：双网络结构（Actor-Critic）

ADP 的所有算法都基于评价网络（Critic）+ 执行网络（Actor） 解耦设计，这是其核心标识，将 "价值估计" 和 "策略生成" 分开，实现独立学习、互相优化，也是后续 RL 中 Actor-Critic 算法的源头。

（1）评价网络（Critic）

• 核心作用 ：逼近价值函数
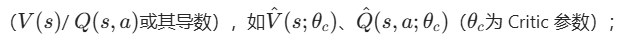
• 学习目标 ：最小化贝尔曼误差 （预测价值与贝尔曼最优方程的目标价值的误差），这是 ADP 的唯一损失函数；
• 本质：代替传统 DP 的 "价值迭代"，用数据驱动更新价值函数。

（2）执行网络（Actor）

• 核心作用 ：逼近策略 ，
• 学习目标 ：基于评价网络的价值估计，贪心 / 梯度上升选择动作，使价值函数最大化；
• 本质：代替传统 DP 的 "策略提取 / 改进"，用数据驱动更新策略。

双网络的通俗理解 ：评价网络是 "裁判"，评估当前动作 / 状态的 "好坏"；执行网络是 "运动员"，根据裁判的评价，调整动作以变得 "更优秀"，两者形成闭环学习。

3. ADP 的核心分类：三大经典算法（Werbos 原创，所有 ADP 的基础）

根据评价网络逼近的对象 ，ADP 分为三类，由浅入深、复杂度递增，收敛速度也逐步提升，初学者先掌握 HDP ，再拓展 DHP/GDHP。三者的核心区别在于逼近的价值函数形式，执行网络的学习方式随评价网络适配，以下是详细对比 + 核心公式 + 学习步骤（知其然亦知其所以然）：

（1）启发式动态规划（HDP）------ 最简单的 ADP（入门必学）

适用场景 ：离散动作空间 的简单非线性系统控制（如简易机器人路径规划、格子世界控制）；逼近对象 ：状态价值函数V(s) ，评价网络为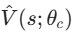（常用单隐层神经网络 / 线性回归）；执行网络 ：无需单独训练，直接由贪心策略 生成动作（基于评价网络的预测），是 HDP 的最大特点：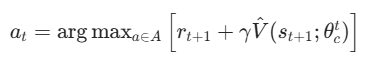

关键 ：是执行动作a后从系统中获取的实际数据，无需任何模型。

HDP 的在线自适应学习步骤（闭环迭代，核心中的核心）

HDP 是在线实时学习 ，全程与系统交互，无离线训练，步骤循环执行直到收敛，每一步都有明确的物理意义 ：前提：系统P/R未知，状态S可连续 / 高维，动作A离散，函数逼近器为神经网络V^(s;θc​)，学习率α（参数更新步长），折扣因子γ。

1. 初始化 ：随机 / 全零初始化评价网络参数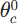，获取系统初始状态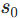，设置迭代步t=0；
2. 执行动作，获取实际交互数据 ：基于当前评价网络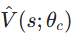，贪心生成动作α，将α作用于系统，直接获取实际数据：即时回报rt+1、下一个状态st+1（无需P/R，数据驱动的核心）；
3. 计算贝尔曼目标（Critic 的学习目标） ：用实际数据代替模型，计算状态st的理想目标价值 ，这是贝尔曼最优方程的数据化形式 （ADP 的核心巧思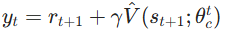）：「通俗解释」：yt是st的 "真实价值"，由实际即时回报 +折扣后的下一个状态预测价值组成，完全从数据中得到；
4. 计算贝尔曼误差（Critic 的损失函数） ：评价网络的唯一学习目标是最小化预测价值与贝尔曼目标的均方误差（MSE） ，误差越小，价值估计越接近最优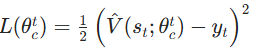：「核心意义」：贝尔曼误差是 ADP 的核心损失，其大小表示 "当前价值估计与贝尔曼最优方程的差距"；
5. 更新评价网络参数（梯度下降） ：通过梯度下降法 最小化损失L，更新θc，这是 ADP "自适应学习" 的关键（机器学习与 DP 的结合）：① 计算损失对θct的梯度：；
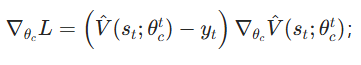6. ② 梯度下降更新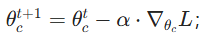：；「通俗解释」：梯度表示 "参数让损失变大的方向"，负梯度更新让损失逐步减小，价值估计越来越准；
7. 收敛判断与迭代 ：若参数更新幅度∥θct+1−θct∥<ϵ（ϵ为预设精度），停止学习，当前贪心策略即为最优自适应策略；否则令t=t+1，st=st+1，返回步骤 2 继续交互学习。

HDP 的核心亮点 ：全程仅需单步交互数据，无需模型、无需离线训练，实时更新、自适应时变系统，完美解决 DP 的 3 个局限。

（2）双启发式动态规划（DHP）------ 适配连续动作空间的 ADP

适用场景 ：连续状态 / 动作空间 的复杂非线性系统控制（如倒立摆稳定、机器人关节控制、无人机悬停），这是工业界最常用的 ADP 算法；核心改进 ：HDP 仅逼近V(s)，适合离散动作；DHP逼近状态价值函数的导数∂V(s)/∂s ，评价网络为V^′(s;θc​)=∂V^(s;θc​)/∂s；执行网络 ：不再是简单贪心，而是通过梯度上升法 求解最优连续动作（利用价值函数的导数，对连续动作求导找极值），公式为：a∗=argmaxa​[r(s,a)+γV^′(s′;θc​)⋅∂a∂s′​]核心优势 ：引入导数后，利用最优控制的伴随方程 加速学习，收敛速度远快于 HDP ，且天然适配连续动作空间（控制工程的核心需求）；学习步骤 ：与 HDP 基本一致，仅将 "逼近V(s)" 改为 "逼近∂V(s)/∂s"，损失函数为导数的贝尔曼误差，其余闭环交互、梯度下降更新完全相同。

（3）全局双启发式动态规划（GDHP）------ 高精度 ADP（进阶）

适用场景 ：高精度、高要求 的复杂非线性系统控制（如自动驾驶轨迹规划、精密机器人操作）；核心改进 ：结合 HDP 和 DHP 的优点，同时逼近V(s)和其导数∂V(s)/∂s （两个评价网络，分别学习），利用全局价值信息 优化策略；核心优势 ：收敛速度最快、精度最高 ，能处理强非线性、快时变的复杂系统；不足：结构最复杂，计算量最大，对硬件实时性要求较高（需高性能控制器）。

4. 三类 ADP 算法的核心对比（一张表掌握）

算法	逼近对象	动作空间	结构复杂度	收敛速度	计算量	工业适用度
HDP	V(s)	离散	极低	慢	小	低（简易控制）
DHP	∂V(s)/∂s	连续 / 离散	中	中	中	高（主流工业控制）
GDHP	V(s)+∂V(s)/∂s	连续 / 离散	高	快	大	极高（高精度控制）

5. ADP 的核心特性

ADP 诞生于控制工程领域，因此其所有设计都围绕控制工程的核心要求，这是与 RL 最本质的区别之一，务必牢记：

1. 严格的稳定性 ：ADP 算法通过李雅普诺夫稳定性理论 严格证明，能保证智能体 - 系统闭环的全局渐近稳定 （控制工程的首要要求，如倒立摆不会倒、机器人不会失控）；
2. 强收敛性 ：基于压缩映射定理和梯度下降的收敛性，ADP 的参数更新和价值函数必然收敛到最优解，无发散风险；
3. 在线实时性 ：无需离线训练，与系统边交互、边学习、边控制，响应时变系统的速度极快；
4. 高数据效率 ：仅需少量单步交互数据即可学习，无需大量试错（因为基于贝尔曼方程的递推优化，比纯试错更高效）；
5. 弱探索性 ：几乎不做探索（仅贪心利用），因为控制工程中试错成本极高（如机器人试错可能碰撞、倒立摆试错会倒），不允许无意义的探索。

四、Actor-Critic与Critic网络

传统 Actor-Critic（AC）：双网络分工协作（基础 + 进阶）

传统 AC 是 "Actor（执行者）+ Critic（评论家）" 双网络结构，核心是 "Critic 评价值，Actor 学策略"，分工明确，适配连续动作，是文献中复杂控制场景的基础。

1. 核心组件：Actor 和 Critic 的 "分工与协作"

（1）Actor（执行者）

• 角色：直接学习 "策略"（状态→动作的映射），比如文献中 "状态s→推力τ" 的映射；
• 输出 ：
  • 离散动作：输出每个动作的选择概率（π(a∣s)）；
  • 连续动作：输出动作的具体值（a=π(s;θa)，θa是 Actor 参数）；
• 目标：学习能让 "累计回报最大" 的策略，更新方向由 Critic 的 "评价" 决定。

（2）Critic（评论家）

• 角色：学习 "价值函数"（V(s)或Q(s,a)），评价 Actor 输出动作的 "好坏"；
• 输出：状态s的价值V(s)（或状态s+ 动作a的价值Q(s,a)）；
• 目标：准确估计价值函数，给 Actor 提供 "靠谱的评价"（用 TD 误差衡量）。

（3）协作逻辑

1. Actor 根据当前状态s，输出动作a（连续动作如推力τ=2.5）；
2. 动作a作用于系统（如质量 - 弹簧 - 阻尼系统），得到即时回报r和下一个状态s′；
3. Critic 根据(s,a,r,s′)，计算 TD 误差（评价动作a的好坏：误差为正→动作好，误差为负→动作差）；
4. Actor 根据 Critic 的 TD 误差，调整策略参数（让 "好动作" 出现概率更高，"坏动作" 更低）；
5. Critic 根据 TD 误差，更新价值函数参数（让评价更准确）；
6. 重复 1-5，直到策略收敛（文献中跟踪误差稳定在小范围）。

2. 数学原理：核心公式推导（知其所以然）

传统 AC 的更新逻辑基于 "TD 误差" 和 "策略梯度"，以下是简化版公式（贴合文献连续动作场景）：

（1）Critic 的更新（价值函数逼近）

Critic 通常逼近状态价值函数V(s;θc​)（θc​是 Critic 参数），更新目标是最小化 TD 误差的均方误差（MSE）：

• TD 误差定义（评价 Actor 动作的核心）

• Critic 的损失函数（MSE）：

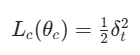
• 梯度下降更新 Critic 参数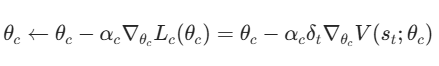：（αc​是 Critic 的学习率，文献中常用αc​=0.001）。

（2）Actor 的更新（策略梯度上升）

Actor 逼近确定性策略a=π(s;θa​)（连续动作场景），更新目标是 "最大化累计回报"，核心是 "策略梯度上升"------ 沿着能提升回报的方向调整θa​：

• 策略梯度的核心逻辑：Actor 的目标是最大化 "基于 Critic 评价的回报"，即E[δt​]（TD 误差的期望，δt​越大，回报越高）；

• Actor 的更新公式（梯度上升）：

• 连续动作场景的具体推导（文献常用）：

单 Critic：单网络 "身兼数职"（简化 + 高效）

单 Critic 是传统 AC 的 "简化版"------ 去掉 Actor 网络，仅用 Critic 逼近价值函数，策略通过 "贪心选择" 生成（argmaxa​Q(s,a)），核心是 "用价值函数直接推导策略"，适配文献中的低开销场景。

1. 核心逻辑：Critic 的 "双重角色"

（1）Critic 的双重任务

• 任务 1：逼近动作价值函数Q(s,a;θc​)（输入：状态s+ 动作a，输出：Q 值）；
• 任务 2：生成策略 ------ 对当前状态s，遍历所有可能动作a，选择 Q 值最大的动作：a∗=argmaxaQ(s,a;θc)（连续动作场景：用 "动作候选集" 或 "梯度上升" 找最优动作）。

（2）学习流程（对应文献 "分布式多智能体"）

1. 单 Critic 根据当前状态s，生成多个动作候选（如推力τ=[1,2,3,4,5]）；
2. 计算每个候选动作的 Q 值，贪心选择 Q 值最大的动作a∗；
3. 动作a∗作用于系统，得到r和s′；
4. 用 TD 误差更新 Critic 的参数（和传统 AC 的 Critic 更新逻辑一致）；
5. 重复 1-4，直到 Q 值收敛，策略稳定。

2. 数学原理：仅需更新 Critic（简化版公式）

单 Critic 的核心是 "Q 值的 TD 更新"，策略生成无额外公式，数学上比传统 AC 简单：

（1）Q 值的 TD 更新

• 

（2）策略生成（无额外公式）