神经网络的简单实现

深度学习基础核心工具库functions.py

深度学习基础核心工具库 的纯 NumPy 实现，完整封装了神经网络训练 / 预测所需的5 类激活函数 和2 类损失函数 ，所有函数均适配标量、向量、矩阵多维度输入，解决了数值溢出、维度不兼容等工程问题，是手写数字识别等神经网络任务的基础依赖组件。

代码整体分为激活函数 、损失函数 、测试代码三部分，以下逐模块详细解析，包含核心作用、实现原理、关键技巧和使用场景：

一、激活函数

1. 阶跃函数（step_function）

# x传入标量
def step_function0(x):
    if x >= 0:
        return 1
    else:
        return 0

# x传入向量或矩阵
def step_function(x):
    return np.array(x >= 0, dtype=int)

核心作用 ：最基础的二值激活函数，将输入划分为「0/1」两类，是感知机的核心组件，用于理论讲解；

双版本实现：

• step_function0：仅支持标量输入，通过条件判断实现二值输出；
• step_function：支持向量 / 矩阵输入 ，利用np.array(x >= 0, dtype=int)实现向量化计算，返回与输入同形状的 0/1 数组；

缺点 ：函数不连续、导数恒为 0，无法通过梯度下降训练，实际神经网络中几乎不使用，仅作理论参考。

2. Sigmoid 函数（sigmoid）

def sigmoid(x):
    return 1/(1 + np.exp(-x))

核心作用 ：经典 S 型激活函数，将任意输入映射到 **(0,1)** 区间，是早期神经网络隐藏层的主流选择；

实现原理：基于公式 sigmoid(x)=1+e−x1​，利用 NumPy 广播机制直接支持多维度输入；

关键特点 ：连续可导（支持梯度下降训练），但存在梯度消失问题（输入绝对值过大时，导数趋近于 0，导致深层网络训练困难）；

使用场景：浅层神经网络的隐藏层（如本次手写数字识别的 2 层隐藏层）。

3. ReLU 函数（relu）

def relu(x):
    return np.maximum(0, x)

• 核心作用 ：目前最主流的隐藏层激活函数，彻底解决了 Sigmoid 的梯度消失问题，大幅提升深层网络的训练效率；
• 实现原理 ：基于公式 ReLU(x)=max(0,x)，利用np.maximum(0, x)取「0 和输入值的较大值」，计算极快且适配任意维度；
• 关键特点：单侧激活（x>0 时直接输出 x，导数为 1；x≤0 时输出 0，导数为 0），保留有效梯度，训练收敛速度远快于 Sigmoid；
• 使用场景：浅层 / 深层神经网络的隐藏层（可直接替换本次手写数字识别的 Sigmoid，提升精度）。

4. Softmax 函数（softmax）

# 一维版：单样本向量输入
def softmax0(x):
    x = x - np.max(x)  # 溢出对策：核心技巧，避免指数爆炸
    return np.exp(x) / np.sum(np.exp(x))

# 通用版：支持一维向量/二维矩阵（N个样本×C个类别）
def softmax(x):
    if x.ndim == 2:  # 处理批量样本
        x = x.T      # 转置为C×N，方便按列（每个样本）计算
        x = x - np.max(x, axis=0)    # 按列减每个样本的最大值
        y = np.exp(x) / np.sum(np.exp(x), axis=0)  # 按列求和，保证每列和为1
        return y.T   # 转置回N×C，恢复原始样本维度
    # 处理单样本向量
    x = x - np.max(x)
    return np.exp(x) / np.sum(np.exp(x))

核心作用 ：专门用于分类任务的输出层 ，将网络输出的原始数值（logits，可正可负）映射到 **(0,1)** 区间，且所有输出值求和为 1 ，使其具备概率分布的含义（如输出 [0.1, 0.8, 0.1] 表示 3 类的预测概率分别为 10%、80%、10%）；

核心解决问题 ：数值溢出 ------ 直接计算np.exp(x)时，若 x 值较大（如 x=100），指数结果会超出浮点数范围导致报错，因此先执行x = x - np.max(x)（输入值减去自身最大值，保证最大值为 0，np.exp(0)=1，从根本避免溢出）；

双版本实现：

• softmax0：仅支持一维向量输入（单样本预测）；
• softmax：通用版，同时支持一维向量（单样本） 和二维矩阵（N×C，N 个样本、C 个类别） ，矩阵输入时按样本维度（行） 计算，保证每个样本的输出概率和为 1；

实现细节 ：矩阵输入时通过转置（x.T）将「N×C」转为「C×N」，方便按列（每个样本）执行减最大值、求和操作，最后再转置回原形状，保证输出与输入维度一致；

使用场景：所有分类任务的输出层（如本次手写数字识别的 10 分类输出层，输出 0-9 的概率分布）。

5. 恒等函数（identity）

def identity(x):
    return x

核心作用 ：输入与输出完全一致（y=x），专门用于回归任务的输出层；

实现原理：极简实现，无任何计算开销，支持任意维度输入；

使用场景：回归任务（如房价预测、温度预测），需输出连续数值，无需做概率映射；与本次手写数字识别的分类任务无关，仅作完整工具库补充。

二、损失函数

1. 均方误差（Mean Squared Error, MSE）

def mean_squared_error(y, t):
    return 0.5 * np.sum((y - t) ** 2)

核心作用 ：专门用于回归任务的损失函数，计算预测值与真实值的「平方误差的平均值」；

实现原理：基于公式 MSE(y,t)=21​∑i=1n​(yi​−ti​)2，利用 NumPy 向量化计算，适配任意维度输入；

关键技巧 ：乘以 0.5 是为了简化后续梯度计算------ 对 MSE 求导时，平方的系数 2 会与 0.5 抵消，最终导数为(y−t)，无需额外计算系数；

特点：误差越大，损失值增长越快，连续可导，梯度下降训练稳定；

使用场景：回归任务（如房价预测），与本次手写数字识别的分类任务无关。

2. 交叉熵误差（Cross Entropy Error, CEE）

def cross_entropy_error(y, t):
    # 一维→二维：单样本转换为批量格式，统一计算逻辑
    if y.ndim == 1:
        y = y.reshape(1, y.size)
        t = t.reshape(1, t.size)

    # 独热编码→类别索引：兼容两种标签格式，无需额外预处理
    if t.size == y.size:
        t = t.argmax(axis=1)

    n = y.shape[0]  # 样本数量
    # 高级索引取真实类别概率，加1e-7避免log(0)，求和后归一化
    return -np.sum(np.log(y[np.arange(n), t] + 1e-7)) / n

核心作用 ：专门用于分类任务 的损失函数，是分类任务的首选损失函数------ 对「预测错误的类别」惩罚更显著，训练收敛速度远快于 MSE；

核心解决问题 ：对数无意义------ 当模型预测概率yi​=0时，log(yi​)会出现无穷大错误，因此在预测值后加1e−7（极小值，不影响概率大小），保证对数计算有定义；

关键特性 ：维度兼容 + 标签格式兼容，无需额外预处理即可直接使用：

1. 适配「一维向量（单样本）」和「二维矩阵（N 个样本）」，自动将一维输入转换为二维，统一计算逻辑；
2. 兼容独热编码标签 （t 为 one-hot，如 [0,1,0]，表示第 2 类为真实标签）和类别索引标签 （t 为整数，如 1），若检测到 t 为独热编码（t.size == y.size），会自动通过argmax(axis=1)转换为类别索引；

实现原理：基于公式 CEE(y,t)=−n1​∑i=1n​log(yi,ti​​+1e−7)，其中n为样本数，ti​为第i个样本的真实类别索引，yi,ti​​为对应类别的预测概率；

关键细节 ：通过y[np.arange(n), t]快速取每个样本「真实类别对应的预测概率」（NumPy 高级索引），避免循环，计算高效；最后除以样本数n归一化，保证损失值大小与样本数无关，适配批量训练；

使用场景：所有分类任务（如本次手写数字识别的 10 分类任务，搭配 Softmax 输出层使用）。

三、测试代码

if __name__ == '__main__':
    # 测试输入：4×3矩阵（4个样本，每个样本3个类别）
    x = np.array([[0, 1, 2], [3, 4, 5], [-1, -2, -3], [-6, -4, -5]])
    print(softmax(x))  # 输出4×3矩阵，每行和为1

这部分是Softmax 函数的专项测试代码 ，作用是验证通用版softmax对二维矩阵输入（批量样本） 的处理能力，确保满足分类任务的核心要求。

四、完整functions.py

import numpy as np

# 一、激活函数
# 1. 阶跃函数
# x传入标量
def step_function0(x):
    if x >= 0:
        return 1
    else:
        return 0

# x传入向量或矩阵
def step_function(x):
    return np.array(x >= 0, dtype=int)

# 2. Sigmoid 函数
def sigmoid(x):
    return 1/(1 + np.exp(-x))

# 3. ReLU 函数
def relu(x):
    return np.maximum(0, x)

# 4. Softmax函数
# 输入x为向量
def softmax0(x):
    # 溢出对策
    x = x - np.max(x)
    return np.exp(x) / np.sum(np.exp(x))

# 输入x为矩阵 N×C
def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)    # 减去每条数据中xi的最大值
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T
    # 溢出对策
    x = x - np.max(x)
    return np.exp(x) / np.sum(np.exp(x))

# 5. 恒等函数
def identity(x):
    return x

# 二、损失函数
# 1. MSE
def mean_squared_error(y, t):
    return 0.5 * np.sum((y - t) ** 2)

# 2. 交叉熵误差
def cross_entropy_error(y, t):
    # 对于一维情况，直接转换为二维
    if y.ndim == 1:
        y = y.reshape(1, y.size)
        t = t.reshape(1, t.size)

    # t 是独热编码表示，转换为正确类别标签的索引
    if t.size == y.size:
        t = t.argmax(axis=1)

    n = y.shape[0]
    return -np.sum(np.log(y[np.arange(n), t] + 1e-7)) / n

# 测试
if __name__ == '__main__':
    x = np.array([[0, 1, 2], [3, 4, 5], [-1, -2, -3], [-6, -4, -5]])

    print(softmax(x))

3 层全连接神经网络前向传播

深度学习入门经典的 3 层全连接前馈神经网络 实现，基于 NumPy 完成从输入层→隐藏层→输出层的前向传播计算，无训练逻辑，仅实现固定参数下的 "数据正向流动计算"，是理解神经网络核心原理的基础。

代码整体分为网络参数初始化 、前向传播计算 、实际调用执行三部分，先明确核心概念，再逐行拆解逻辑、补充计算细节和原理。

定义并初始化神经网络的所有权重（W）和偏置（b），用字典存储（键为参数名，值为 NumPy 数组），保证参数按层索引，返回完整的网络参数字典。

def init_network():
    # 新建空字典，用于存储各层权重和偏置
    network = {}
    # 输入层→隐藏层1的权重：2行（输入层2神经元）×3列（隐藏层1 3神经元），符合「前层×后层」规则
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    # 隐藏层1的偏置：长度3，与隐藏层1神经元数一致
    network['b1'] = np.array([0.1, 0.2, 0.3])
    # 隐藏层1→隐藏层2的权重：3行（隐藏层1 3神经元）×2列（隐藏层2 2神经元）
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    # 隐藏层2的偏置：长度2，与隐藏层2神经元数一致
    network['b2'] = np.array([0.1, 0.2])
    # 隐藏层2→输出层的权重：2行（隐藏层2 2神经元）×2列（输出层2神经元）
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    # 输出层的偏置：长度2，与输出层神经元数一致
    network['b3'] = np.array([0.1, 0.2])
    # 返回包含所有参数的网络字典
    return network

实现数据从输入层到输出层的逐层计算 ，是神经网络的执行核心。参数network为init_network()返回的参数字典，x为输入数据（NumPy 数组），返回最终输出结果y。

def forward(network, x):
    # 从网络字典中解包各层权重和偏置，简化后续代码书写（无需重复写network['W1']）
    w1, w2, w3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    # 第1层计算：输入层 → 隐藏层1
    a1 = np.dot(x, w1) + b1  # 线性变换：输入x与权重w1点积 + 偏置b1（NumPy广播自动适配形状）
    z1 = sigmoid(a1)         # 非线性激活：sigmoid处理线性结果a1，引入非线性，得到隐藏层1输出
    
    # 第2层计算：隐藏层1 → 隐藏层2
    a2 = np.dot(z1, w2) + b2 # 线性变换：上一层激活输出z1作为输入，与w2点积 + b2
    z2 = sigmoid(a2)         # 非线性激活：隐藏层统一用sigmoid，得到隐藏层2输出
    
    # 第3层计算：隐藏层2 → 输出层
    a3 = np.dot(z2, w3) + b3 # 线性变换：最后一次线性计算，无后续隐藏层
    y = identity(a3)         # 输出层激活：恒等函数，直接输出a3（回归任务无需映射）

    return y

完整代码

import numpy as np
from functions import sigmoid, identity

def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

def forward(network, x):
    w1, w2, w3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, w1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, w2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, w3) + b3
    y = identity(a3)

    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)

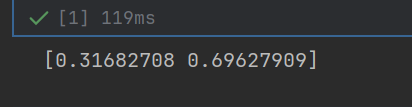
print(y)

运行结果：

应用案例：手写数字识别

基于预训练模型的手写数字识别预测程序 ，核心实现MNIST 数据集加载预处理 +预训练神经网络模型加载 +批量预测 +识别精度评估 的全流程，基于 NumPy、Pandas 和 Scikit-learn 实现，依赖自定义的激活函数工具库functions.py。

一、任务要求

1.任务与数据集说明

任务 ：手写数字识别（0-9 共 10 个类别），属于多分类任务；

数据集 ：MNIST 的train.csv（Kaggle 经典格式），每行是 1 个手写数字样本，第一列label是真实数字（0-9），剩余 784 列是 28×28 像素的灰度值（0-255），即784 个输入特征 →10 个输出类别；

核心依赖 ：functions.py中的sigmoid（隐藏层激活）、softmax（输出层激活，将结果转为概率分布）。

2. 网络与模型说明

神经网络结构：784 输入→N 隐藏 1→M 隐藏 2→10 输出的 3 层全连接网络（权重 / 偏置形状匹配 784 特征 + 10 分类）；

预训练模型：nn_sample是提前训练好的网络参数文件（由joblib保存，包含W1/W2/W3权重矩阵和b1/b2/b3偏置向量），本代码仅做加载和预测，无训练逻辑。

3.思路

批量预测：避免单样本循环计算，提升效率（每次处理 100 个样本）；

归一化：将像素值缩放到 0-1 区间，适配神经网络输入要求；

概率最大化预测 ：通过softmax将网络输出转为 0-1 的概率分布，取概率最大的索引为预测数字；

精度评估：通过「预测值与真实标签匹配数 / 总样本数」计算识别准确率。

二、代码编写

完成 MNIST 数据集的「加载→特征 / 标签拆分→训练 / 测试集划分→归一化」全预处理流程，返回预处理后的测试集特征 和测试集真实标签，为后续预测做数据准备。

def get_data():
    # 1. 加载MNIST数据集（train.csv放在代码同级目录）
    data = pd.read_csv("train.csv")
    # 2. 拆分特征矩阵X和真实标签y
    X = data.drop("label", axis=1)  # 特征：删除label列，剩余784列（28×28像素），DataFrame格式
    y = data["label"]               # 标签：仅保留label列，值为0-9的整数，Series格式
    # 3. 划分训练集（70%）和测试集（30%），test_size=0.3表示测试集占30%
    # 注：本代码无训练逻辑，训练集实际未使用，仅为保持预处理流程完整性
    x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
    # 4. 初始化归一化器：MinMaxScaler将数据缩放到[0,1]区间，公式：X_scaled = (X - X_min) / (X_max - X_min)
    preprocessor = MinMaxScaler()
    # 5. 训练集拟合+转换：拟合训练集的最大值/最小值，仅用训练集的统计信息做归一化（避免数据泄露）
    x_train = preprocessor.fit_transform(x_train)
    # 6. 测试集仅转换：直接使用训练集的最大值/最小值，保证训练/测试集归一化标准一致
    x_test = preprocessor.transform(x_test)
    # 修正后返回：预处理后的测试集特征、测试集真实标签（原代码t_test改为y_test）
    return x_test, y_test

关键细节说明

• 数据泄露避免 ：fit_transform仅用在训练集，transform用在测试集，是机器学习预处理的黄金准则，防止测试集的统计信息影响模型泛化能力；
• 数据格式转换 ：Pandas 的 DataFrame/Series 经fit_transform后，会自动转为NumPy 数组（适配后续神经网络的矩阵计算）；
• 归一化的必要性 ：MNIST 像素值为 0-255，若不归一化，大数值会导致sigmoid激活函数进入饱和区（导数趋近于 0），即使是预测阶段，也会导致网络输出异常，精度骤降。

实现 3 层全连接神经网络的前向传播计算 ，接收预训练模型参数和输入数据，返回每个样本对应 10 个数字的概率分布，是手写数字识别的「预测核心」。

def predict(network, x):
    # 1. 从网络参数字典中解包权重和偏置，简化后续计算
    w1, w2, w3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    # 2. 第一层计算：输入层 → 隐藏层1（线性变换+非线性激活）
    a1 = np.dot(x, w1) + b1  # 线性变换：输入x与权重w1矩阵点积 + 偏置b1（NumPy广播自动适配形状）
    z1 = sigmoid(a1)         # 非线性激活：sigmoid将线性结果映射到(0,1)，引入非线性特征提取

    # 3. 第二层计算：隐藏层1 → 隐藏层2（重复线性+激活流程）
    a2 = np.dot(z1, w2) + b2 # 上一层激活输出z1作为当前层输入
    z2 = sigmoid(a2)         # 隐藏层统一使用sigmoid激活

    # 4. 第三层计算：隐藏层2 → 输出层（线性变换+softmax概率化）
    a3 = np.dot(z2, w3) + b3 # 最后一次线性变换，得到10个原始输出值（logits）
    y = softmax(a3)          # softmax将原始值转为(0,1)的概率分布，且10个概率和为1

    return y

关键细节说明

• 批量输入适配 ：函数的输入x可以是单样本向量（1×784）或批量样本矩阵（N×784） ，NumPy 的np.dot和广播机制会自动适配，返回对应形状的概率分布（1×10 或 N×10），这是向量化计算的核心优势，无需循环单样本；
• softmax 的核心作用 ：将网络输出的原始值（可正可负、无固定范围）转为概率分布 ，例如输出[0.01, 0.95, 0.04, ..., 0]表示该样本是数字 1 的概率为 95%，是其他数字的概率极低，让输出结果具备直观的概率含义；
• 与回归任务的区别 ：手写数字识别是分类任务，因此输出层用softmax而非恒等函数，后续可通过np.argmax快速取概率最大的类别作为预测结果。

三、完整代码

import numpy as np
import pandas as pd
import joblib
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from functions import sigmoid, softmax

def get_data():
    # 加载数据集
    data = pd.read_csv("train.csv")
    # 划分训练集和测试集
    X = data.drop("label", axis=1)
    y = data["label"]
    x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
    # 归一化
    preprocessor = MinMaxScaler()
    x_train = preprocessor.fit_transform(x_train)
    x_test = preprocessor.transform(x_test)
    return x_test, t_test

    def init_network():
        # 加载模型
        network = joblib.load("nn_sample")
        return network

def predict(network, x):
    w1, w2, w3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, w1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, w2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, w3) + b3
    y = softmax(a3)

    return y


x, t = get_data()
network = init_network()

batch_size = 100 # 批数量
accuracy_cnt = 0

for i in range(0, len(x), batch_size):
    x_batch = x[i:i+batch_size]
    y_batch = predict(network, x_batch)
    p = np.argmax(y_batch, axis=1)
    accuracy_cnt += np.sum(p == t[i:i+batch_size])

print("Accuracy:" + str(float(accuracy_cnt) / len(x)))

运行结果：

结果1

结果2