1.无穷远处的极限
2.渐近线
3.e的极限表示
1.无穷远处的极限
csharp
极限的三种经典趋势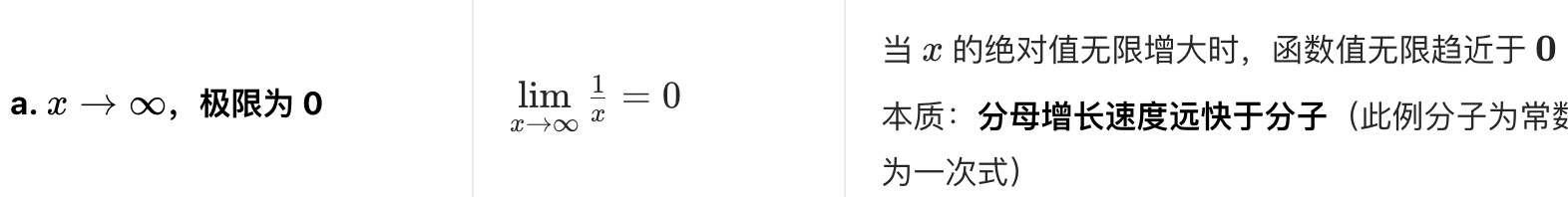
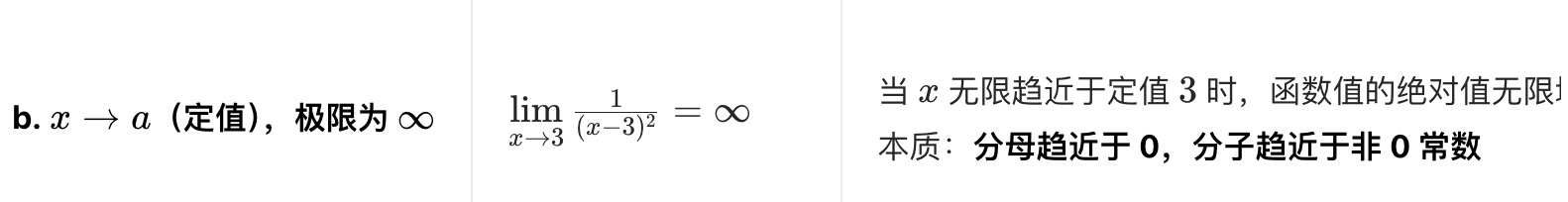

2.渐近线
csharp
函数的图形离原点的距离越来越远时, 图形与某些直线非常非常接近0, 那我们就说这个函数
非常非常接近这个直线, 将这个直线称为图形的渐近线(注: 渐近线可以与图形相交)
csharp
1).水平渐近线是平行于x轴的直线, 形式为y = k, 它本质上是斜渐近线当斜率m = 0时的特殊
情况; 若直线y = k是函数y = f(x)的水平渐近线, 则满足以下任一极限条件:
csharp
核心特征: 当x趋向正无穷或负无穷时, 函数图像会无限贴近直线y = k, 但不会与该直线相交;
一个函数最多有两条水平渐近线
csharp
2).垂直渐近线是垂直于x轴的直线(形式x = a),满足以下任一条件
csharp
核心特征: 函数在x = a处无定义, 且当x无限靠近a时, 函数值会无限增大/减小, 图像会无限
贴近直线x = a但永远不会相交
csharp
3).斜渐近线
函数y = f(x)的斜渐近线y = m * x + k, 则满足lim x->∞ (f(x) - m * x - k) = 0
或lim x->-∞ (f(x) - m * x - k) = 0(注: m = 0, 则该直线是水平渐近线)
csharp
斜渐近线的计算方法
a.计算斜率m
csharp
b.计算截距k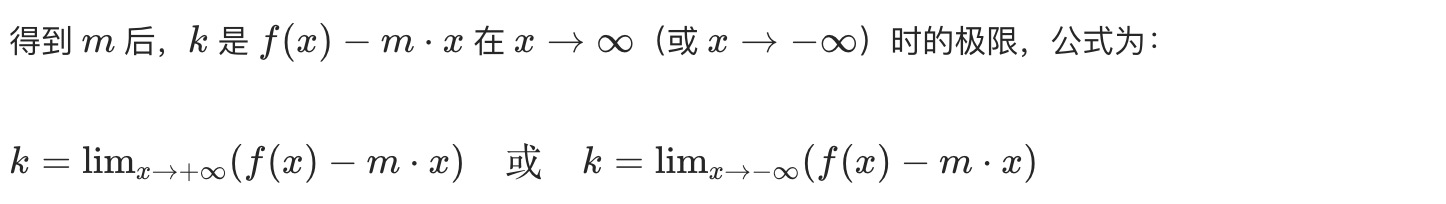
csharp
示例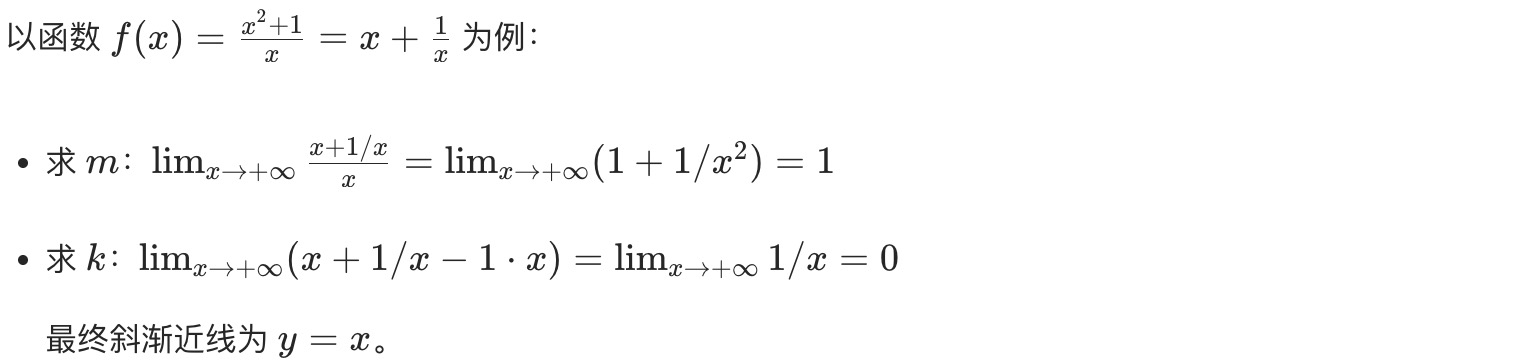

csharp
思路: ∞−∞ 是未定式, 需要通过有理化转化为可计算的形式

3.e的极限表示
csharp
e的标准极限定义
csharp
令t = 1/n, n趋近于无穷大, 则t趋近于0
csharp
当t足够接近0时, 可以得出