【数学】【微积分】④ 从变化率到世界优化：微积分的现代应用与实战解析

📖目录

前言：微积分------世界的数学语言
[1. 微积分：从"瞬时速度"到"变化率"的革命](#1. 微积分：从"瞬时速度"到"变化率"的革命)
- [1.1 为什么需要微积分？](#1.1 为什么需要微积分？)
- [1.2 导数的严格定义：极限的力量](#1.2 导数的严格定义：极限的力量)
[2. 导数的计算法则：从基础到实战](#2. 导数的计算法则：从基础到实战)
- [2.1 基本导数公式：记住这些"数学常量"](#2.1 基本导数公式：记住这些"数学常量")
- [2.2 导数的四则运算法则](#2.2 导数的四则运算法则)
[3. 导数的核心应用：从变化率到现实世界优化](#3. 导数的核心应用：从变化率到现实世界优化)
- [3.1 微分中值定理：沟通局部与整体的桥梁](#3.1 微分中值定理：沟通局部与整体的桥梁)
- [3.2 洛必达法则：解决极限难题的利器](#3.2 洛必达法则：解决极限难题的利器)
- [3.3 函数的单调性与极值：寻找最优解](#3.3 函数的单调性与极值：寻找最优解)
[4. 微积分在现代科技中的应用](#4. 微积分在现代科技中的应用)
- [4.1 机器学习：梯度下降法](#4.1 机器学习：梯度下降法)
- [4.2 金融工程：期权定价](#4.2 金融工程：期权定价)
[5. 积分与微分：一对孪生兄弟](#5. 积分与微分：一对孪生兄弟)
- [5.1 微分与积分关系](#5.1 微分与积分关系)
- [5.2 核心积分公式（对应导数逆运算）](#5.2 核心积分公式（对应导数逆运算）)
- [5.3 积分的四则运算法则](#5.3 积分的四则运算法则)
- [5.4 定积分的实用计算步骤（补充）](#5.4 定积分的实用计算步骤（补充）)
[6. 常见误区与易错点小结](#6. 常见误区与易错点小结)
- [6.1 导数相关误区](#6.1 导数相关误区)
- [6.2 积分相关误区](#6.2 积分相关误区)
- [6.3 跨概念误区](#6.3 跨概念误区)
[7. 实战拓展：综合应用案例（导数+积分）](#7. 实战拓展：综合应用案例（导数+积分）)
- [7.1 物理场景：匀加速运动的路程计算](#7.1 物理场景：匀加速运动的路程计算)
- [7.2 经济场景：边际收益的总收益计算](#7.2 经济场景：边际收益的总收益计算)
[8. 经典参考书推荐](#8. 经典参考书推荐)
- [8.1 数学分析经典](#8.1 数学分析经典)
- [8.2 实用工具书](#8.2 实用工具书)
[9. 结语：微积分------理解变化的艺术](#9. 结语：微积分——理解变化的艺术)
[10. 参考文献](#10. 参考文献)
[11. 下一篇预告](#11. 下一篇预告)
[12. 微积分学习路径：从基础到应用的完整旅程](#12. 微积分学习路径：从基础到应用的完整旅程)
- [12.1 详细学习路径说明（文字版）](#12.1 详细学习路径说明（文字版）)
- - [🌟 **第一阶段：基础概念（1-2周）**](#🌟 第一阶段：基础概念（1-2周）)
  - [🌟 **第二阶段：计算法则（2-3周）**](#🌟 第二阶段：计算法则（2-3周）)
  - [🌟 **第三阶段：应用领域（3-4周）**](#🌟 第三阶段：应用领域（3-4周）)
  - [🌟 **第四阶段：高级应用（4周+）**](#🌟 第四阶段：高级应用（4周+）)
- [12.2 推荐学习顺序（附时间规划）](#12.2 推荐学习顺序（附时间规划）)
- [12.3 学习误区与避坑指南](#12.3 学习误区与避坑指南)
- [12.4 附：推荐学习资源](#12.4 附：推荐学习资源)
- [12.5 为什么这个学习路径有效？](#12.5 为什么这个学习路径有效？)
[13. 往期回顾](#13. 往期回顾)

前言：微积分------世界的数学语言

想象一下，你正在驾驶一辆自动驾驶汽车，它需要实时计算前方障碍物的相对速度，以决定是刹车还是转向。这个过程背后，正是微积分在默默工作。微积分不仅是数学的"皇冠"，更是理解世界变化规律的钥匙。它帮助我们从"变化"中提取规律，从"累积"中发现价值。

为什么微积分如此重要？

它是深度学习、机器学习的数学基础

它是优化算法的核心驱动力

它是理解物理、经济、生物等多学科现象的通用语言

本文将带你从日常生活中理解微积分，避开复杂的数学符号，用大白话和生活实例，揭开微积分的神秘面纱。

1. 微积分：从"瞬时速度"到"变化率"的革命

1.1 为什么需要微积分？

想象你正在和朋友一起骑自行车，你想要知道在某个特定时刻（比如第10分钟）的"瞬时速度"，而不是整段路程的平均速度。

平均速度：总路程 ÷ 总时间
瞬时速度：在某个特定时刻的速度

在没有微积分的时代，人们只能用"极短时间内的平均速度"来近似瞬时速度。例如，从第9分59秒到第10分01秒，你骑行了200米，那么瞬时速度大约是200米/2秒 = 100米/秒。

微积分的诞生，正是为了解决这种"瞬时变化"的计算问题。

1.2 导数的严格定义：极限的力量

导数的严格定义基于极限，这是微积分的基石。函数 y = f ( x ) y = f(x) y=f(x) 在点 x = a x = a x=a 处的导数 f ′ ( a ) f'(a) f′(a) 定义为：

f ′ ( a ) = lim ⁡ Δ x → 0 f ( a + Δ x ) − f ( a ) Δ x f'(a) = \lim_{\Delta x \to 0} \frac{f(a+\Delta x) - f(a)}{\Delta x} f′(a)=Δx→0limΔxf(a+Δx)−f(a)

大白话解释 ：当 Δ x \Delta x Δx（时间间隔）趋近于0时，函数值变化量 Δ y \Delta y Δy 与 Δ x \Delta x Δx 的比值的极限，就是函数在 x = a x = a x=a 处的瞬时变化率。

生活类比：就像你用手机测速时，显示的"瞬时速度"其实是基于极短时间内的距离变化计算的，而不是整段路程的平均速度。

图1：微积分是AI模型训练的"数学引擎"，理解导数是掌握深度学习的关键

函数曲线与切线的可视化：

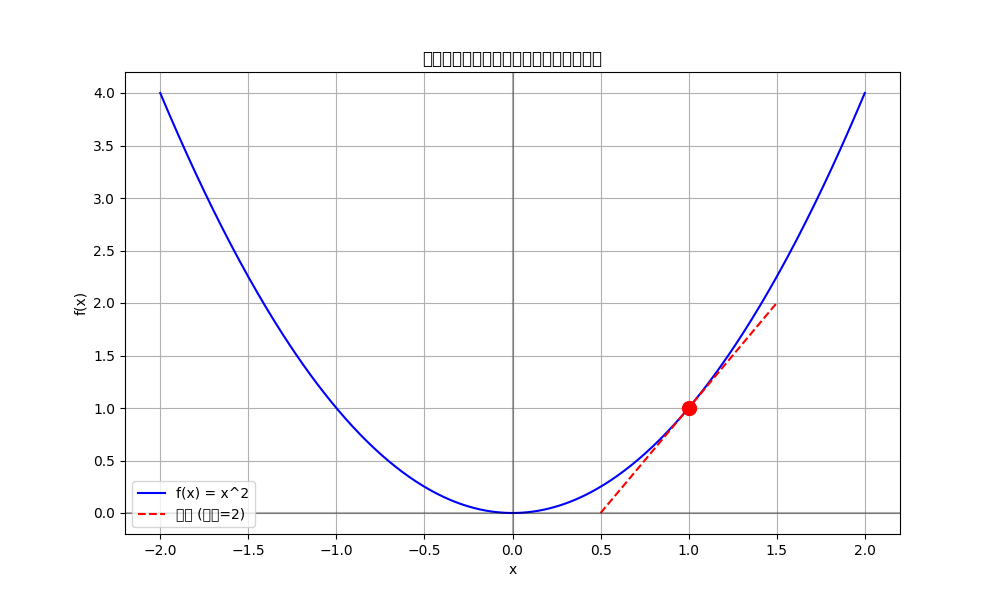
图2：函数 f ( x ) = x 2 f(x) = x^2 f(x)=x2 在 x = 1 x=1 x=1 处的切线斜率是2，这正是导数 f ′ ( 1 ) f'(1) f′(1) 的值

2. 导数的计算法则：从基础到实战

2.1 基本导数公式：记住这些"数学常量"

函数	导数	生活类比
f ( x ) = c f(x) = c f(x)=c (常数)	f ′ ( x ) = 0 f'(x) = 0 f′(x)=0	价格固定不变的奶茶，价格变化率为0
f ( x ) = x n f(x) = x^n f(x)=xn	f ′ ( x ) = n x n − 1 f'(x) = nx^{n-1} f′(x)=nxn−1	奶茶杯的半径增长，体积增长速度
f ( x ) = e x f(x) = e^x f(x)=ex	f ′ ( x ) = e x f'(x) = e^x f′(x)=ex	复利增长，增长率等于当前值
f ( x ) = sin ⁡ x f(x) = \sin x f(x)=sinx	f ′ ( x ) = cos ⁡ x f'(x) = \cos x f′(x)=cosx	摇晃的秋千，速度与角度的关系

为什么 e x e^x ex 的导数是它自己？

e e e 是一个特殊的数（约等于2.718），它的特性是：当 x x x 增加时， e x e^x ex 的增长率恰好等于 e x e^x ex 本身。这就像一个"自增长"的生物，它的生长速度与当前大小成正比。

2.2 导数的四则运算法则

法则	公式	生活类比
加法法则	( f + g ) ′ = f ′ + g ′ (f+g)' = f' + g' (f+g)′=f′+g′	两个人同时跑步，总速度是各自速度之和
乘法法则	( f g ) ′ = f ′ g + f g ′ (fg)' = f'g + fg' (fg)′=f′g+fg′	两人合作做蛋糕，总产量与各自效率和合作时间有关
商法法则	( f g ) ′ = f ′ g − f g ′ g 2 \left(\frac{f}{g}\right)' = \frac{f'g - fg'}{g^2} (gf)′=g2f′g−fg′	两人合作做蛋糕，总产量与各自效率和合作时间的比值

生活例子 ：假设你开了一家奶茶店，每天的收入 R R R 与顾客数量 n n n 和每杯奶茶的利润 p p p 有关， R = n × p R = n \times p R=n×p。如果顾客数量和利润都在变化，那么收入的变化率就是：

R ′ = n ′ p + n p ′ R' = n'p + np' R′=n′p+np′

这正是乘法法则的体现。

3. 导数的核心应用：从变化率到现实世界优化

3.1 微分中值定理：沟通局部与整体的桥梁

拉格朗日中值定理 ：如果函数 f ( x ) f(x) f(x) 在闭区间 [ a , b ] [a, b] [a,b] 上连续，在开区间 ( a , b ) (a, b) (a,b) 内可导，则在 ( a , b ) (a, b) (a,b) 内至少存在一点 ξ \xi ξ，使得：

f ′ ( ξ ) = f ( b ) − f ( a ) b − a f'(\xi) = \frac{f(b) - f(a)}{b - a} f′(ξ)=b−af(b)−f(a)

生活类比：你从A城市到B城市，总路程是100公里，用时2小时。平均速度是50公里/小时。那么在这段路程中，至少存在一个时刻，你的瞬时速度恰好等于50公里/小时。

中值定理示意图

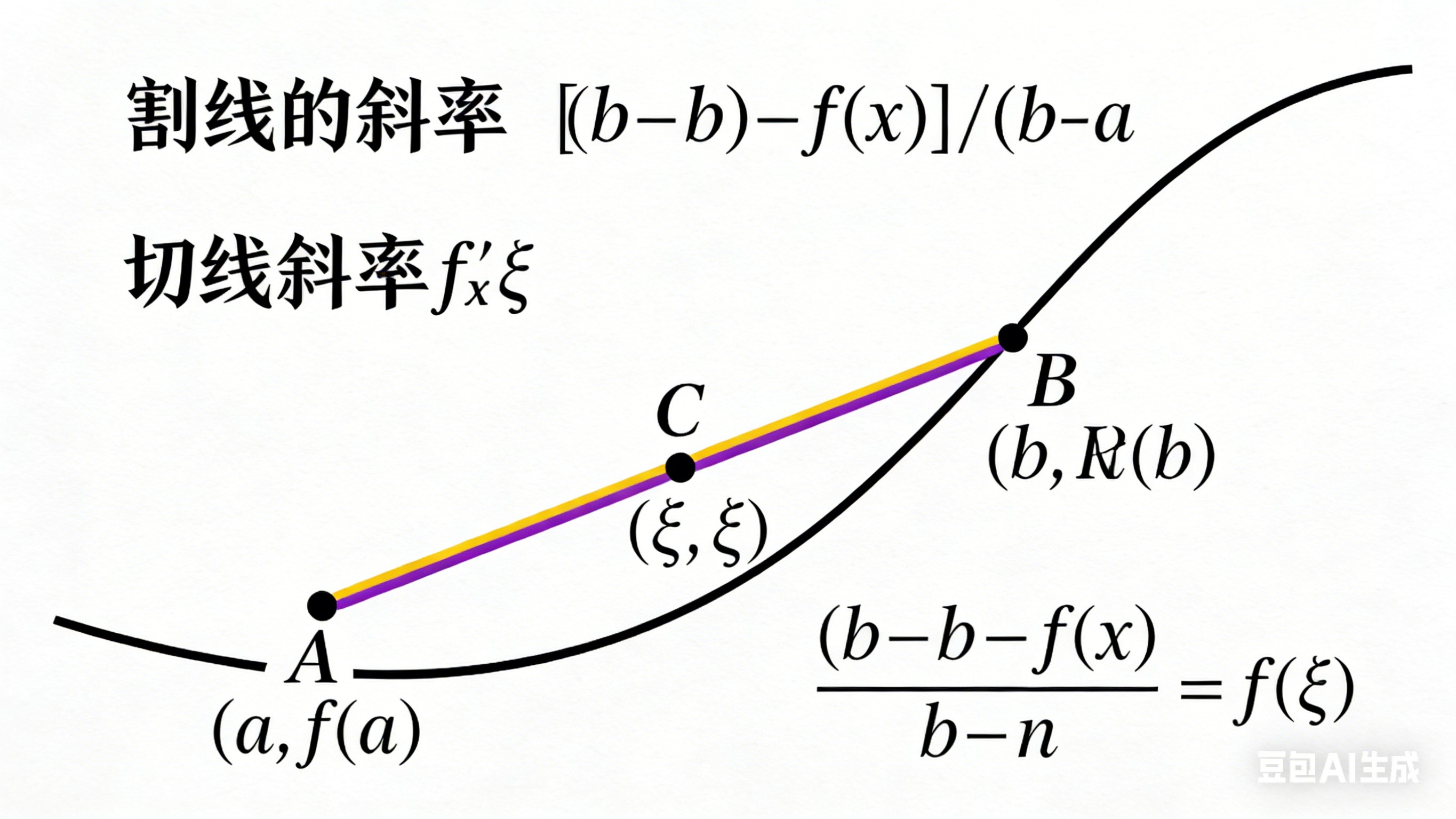
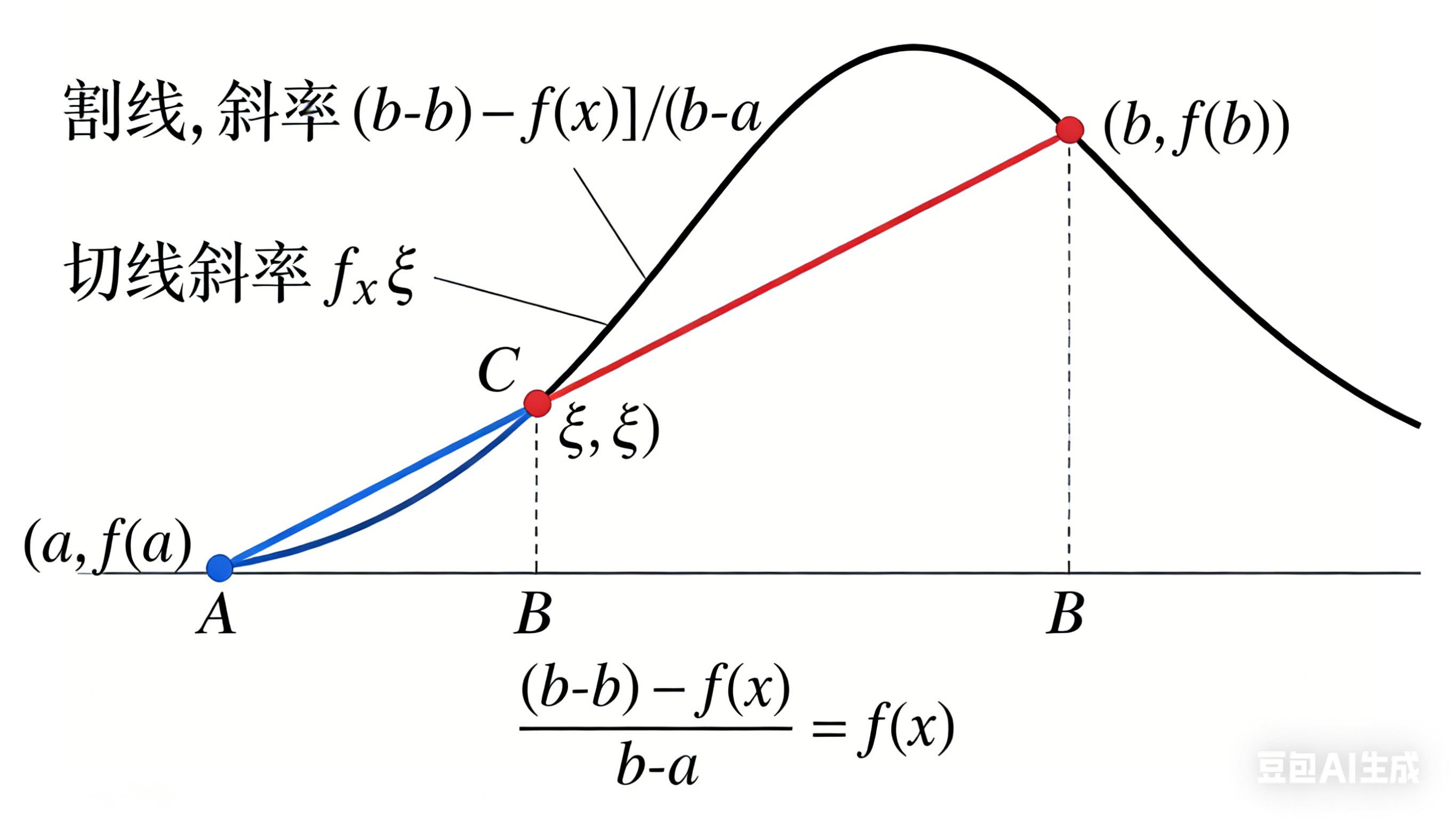
图3：拉格朗日中值定理的几何解释 - 曲线在某点的切线与两点连线平行

3.2 洛必达法则：解决极限难题的利器

洛必达法则 ：当 lim ⁡ x → a f ( x ) g ( x ) \lim_{x \to a} \frac{f(x)}{g(x)} limx→ag(x)f(x) 为 0 0 \frac{0}{0} 00 或 ∞ ∞ \frac{\infty}{\infty} ∞∞ 型不定式时，有：

lim ⁡ x → a f ( x ) g ( x ) = lim ⁡ x → a f ′ ( x ) g ′ ( x ) \lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)} x→alimg(x)f(x)=x→alimg′(x)f′(x)

生活类比：想象你和朋友在玩一个"猜价格"的游戏，当价格接近某个值时，你无法直接猜出准确价格，但可以先猜价格的变化率（导数），然后根据变化率来推断准确价格。

代码实战 ：计算 lim ⁡ x → 0 sin ⁡ x x \lim_{x \to 0} \frac{\sin x}{x} limx→0xsinx

python 复制代码

# 需要先安装三方库：pip3 install sympy
import sympy as sp

x = sp.symbols('x')
expr = sp.sin(x) / x
limit_value = sp.limit(expr, x, 0)
print(f"极限值: {limit_value}")

执行结果：

复制代码

极限值: 1

3.3 函数的单调性与极值：寻找最优解

单调性判定：

如果 f ′ ( x ) > 0 f'(x) > 0 f′(x)>0，函数在该区间单调递增
如果 f ′ ( x ) < 0 f'(x) < 0 f′(x)<0，函数在该区间单调递减

极值点判定：

如果 f ′ ( x ) = 0 f'(x) = 0 f′(x)=0 且 f ′ ′ ( x ) > 0 f''(x) > 0 f′′(x)>0，则 x x x 是极小值点
如果 f ′ ( x ) = 0 f'(x) = 0 f′(x)=0 且 f ′ ′ ( x ) < 0 f''(x) < 0 f′′(x)<0，则 x x x 是极大值点

生活例子：你正在设计一款手机APP，想找到最佳的用户界面布局，使得用户停留时间最长。这实际上是一个极值问题，通过分析导数，你可以找到最优布局。

函数单调性与极值可视化（用Python生成）：

原函数：f(x) = x^3 - 3x^2 + 2

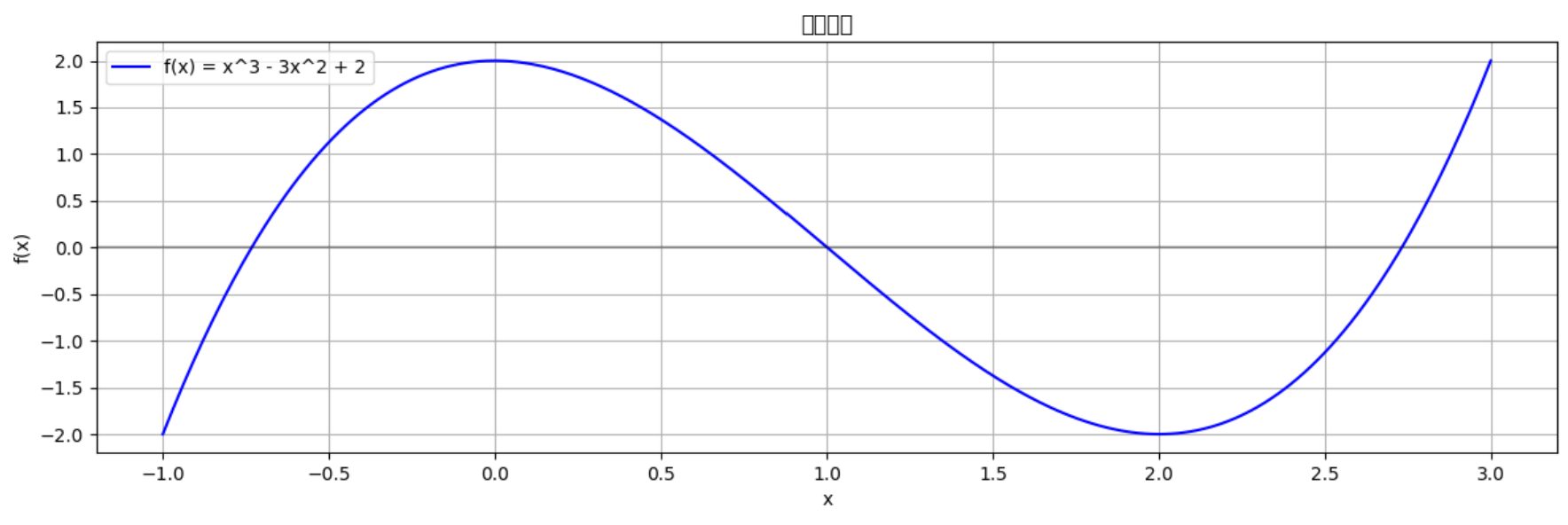
导函数：f'(x) = 3x^2 - 6x

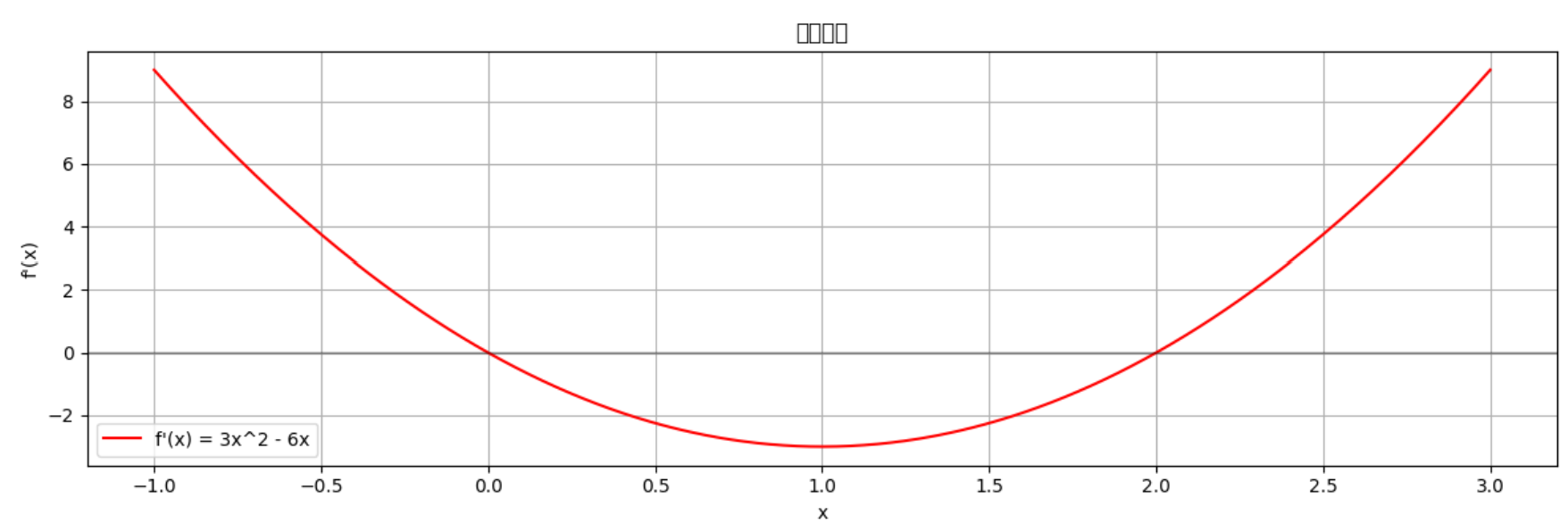
图4：函数 f ( x ) = x 3 − 3 x 2 + 2 f(x) = x^3 - 3x^2 + 2 f(x)=x3−3x2+2 的单调性与极值 - 在 x = 0 x=0 x=0 处有极大值，在 x = 2 x=2 x=2 处有极小值

4. 微积分在现代科技中的应用

4.1 机器学习：梯度下降法

梯度下降是机器学习中最常用的优化算法，其核心思想就是利用导数（梯度）来寻找函数的最小值。

梯度下降公式 ：
θ n + 1 = θ n − α ∇ J ( θ n ) \theta_{n+1} = \theta_n - \alpha \nabla J(\theta_n) θn+1=θn−α∇J(θn)

其中， θ \theta θ 是模型参数， α \alpha α 是学习率， ∇ J ( θ ) \nabla J(\theta) ∇J(θ) 是损失函数 J J J 的梯度。

生活类比：想象你在下山，想最快到达山脚。你每走一步，都向最陡峭的方向（梯度方向）走，这样能最快到达山脚。

梯度下降过程图

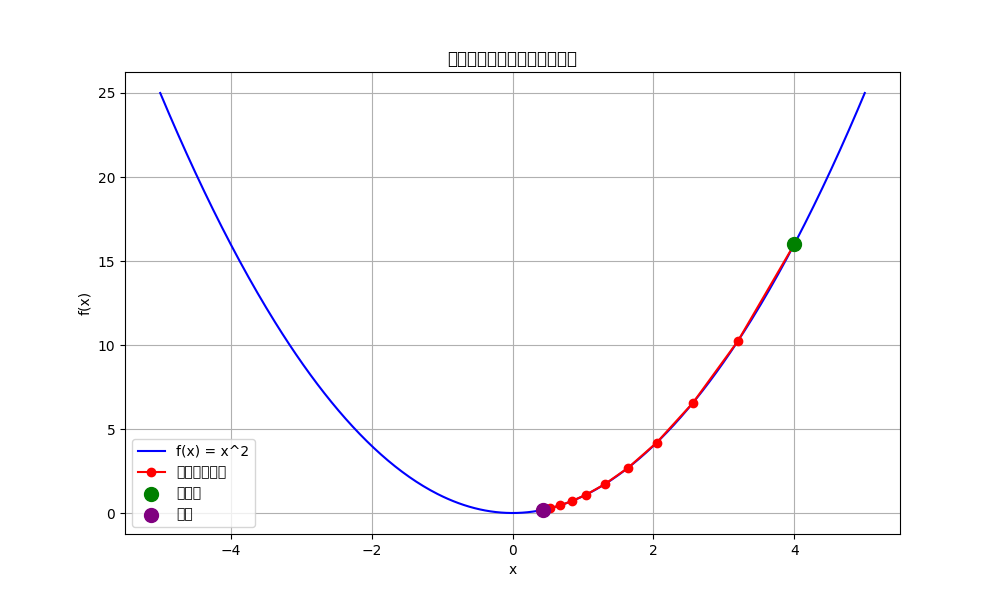
图5：梯度下降法在 f ( x ) = x 2 f(x) = x^2 f(x)=x2 上的优化过程 - 从初始点 x = 4 x=4 x=4 开始，逐步向最小值点 x = 0 x=0 x=0 进发

4.2 金融工程：期权定价

Black-Scholes模型是金融工程中著名的期权定价模型，其核心是偏微分方程：

∂ V ∂ t + 1 2 σ 2 S 2 ∂ 2 V ∂ S 2 + r S ∂ V ∂ S − r V = 0 \frac{\partial V}{\partial t} + \frac{1}{2}\sigma^2 S^2 \frac{\partial^2 V}{\partial S^2} + rS \frac{\partial V}{\partial S} - rV = 0 ∂t∂V+21σ2S2∂S2∂2V+rS∂S∂V−rV=0

其中， V V V 是期权价格， S S S 是标的资产价格， σ \sigma σ 是波动率， r r r 是无风险利率。

生活类比：想象你买了一个期权，相当于买了未来以特定价格买入股票的权利。微积分帮助你计算这个权利的合理价格。

5. 积分与微分：一对孪生兄弟

5.1 微分与积分关系

微积分由两部分组成：微分和积分，它们互为逆运算。

概念	作用	生活类比
微分	计算变化率	速度是位置对时间的导数
积分	计算累积量	距离是速度对时间的积分

简单关系：

如果 f ′ ( x ) = g ( x ) f'(x) = g(x) f′(x)=g(x)，则 ∫ g ( x ) d x = f ( x ) + C \int g(x) dx = f(x) + C ∫g(x)dx=f(x)+C
微分是"切片"，积分是"累积"

生活例子：你开车从A到B，速度随时间变化。微分帮助你计算在某一时刻的瞬时速度，积分帮助你计算总行驶距离。

积分的几何意义可视化：

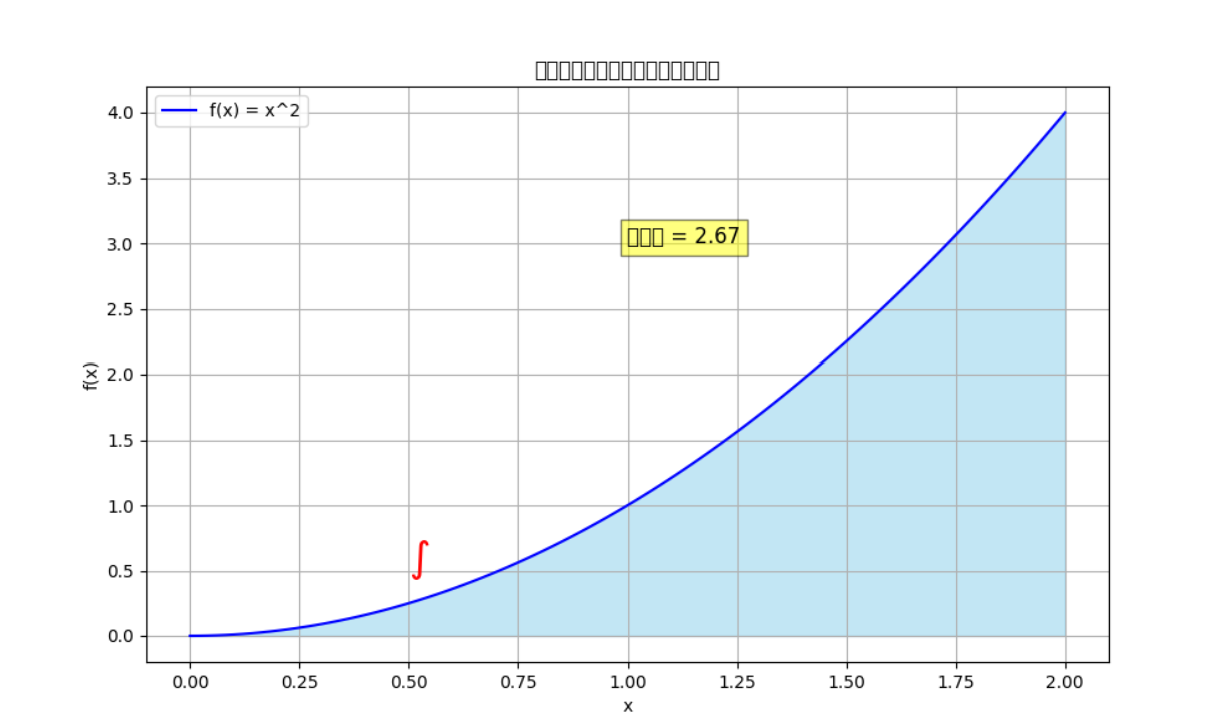
图6：函数 f ( x ) = x 2 f(x) = x^2 f(x)=x2 在区间 [ 0 , 2 ] [0, 2] [0,2] 上的积分 - 曲线下方的面积表示累积量

5.2 核心积分公式（对应导数逆运算）

被积函数	积分结果	生活类比
g ( x ) = 0 g(x) = 0 g(x)=0	∫ 0 d x = C \int 0 dx = C ∫0dx=C	速度始终为0，总距离不变（常数）
g ( x ) = x n g(x) = x^n g(x)=xn（ n ≠ − 1 n \neq -1 n=−1）	∫ x n d x = 1 n + 1 x n + 1 + C \int x^n dx = \frac{1}{n+1}x^{n+1} + C ∫xndx=n+11xn+1+C	奶茶杯体积随半径的累积增长总量
g ( x ) = e x g(x) = e^x g(x)=ex	∫ e x d x = e x + C \int e^x dx = e^x + C ∫exdx=ex+C	复利增长的总收益累积
g ( x ) = cos ⁡ x g(x) = \cos x g(x)=cosx	∫ cos ⁡ x d x = sin ⁡ x + C \int \cos x dx = \sin x + C ∫cosxdx=sinx+C	秋千摆动的总位移累积
g ( x ) = 1 x g(x) = \frac{1}{x} g(x)=x1	$\int \frac{1}{x} dx = \ln	x

5.3 积分的四则运算法则

加法法则： ∫ [ f ( x ) + g ( x ) ] d x = ∫ f ( x ) d x + ∫ g ( x ) d x \int [f(x) + g(x)] dx = \int f(x) dx + \int g(x) dx ∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx
生活类比：两人分别跑步的总距离之和，等于共同跑步的总累积距离
常数乘法法则： ∫ k f ( x ) d x = k ∫ f ( x ) d x \int kf(x) dx = k\int f(x) dx ∫kf(x)dx=k∫f(x)dx（ k k k为常数）
生活类比：速度翻倍时，相同时间内的总距离也翻倍

5.4 定积分的实用计算步骤（补充）

求被积函数的原函数（利用上述公式和法则）
代入上下限，计算差值： ∫ a b f ( x ) d x = F ( b ) − F ( a ) \int_a^b f(x) dx = F(b) - F(a) ∫abf(x)dx=F(b)−F(a)
验证几何意义（曲线下面积、累积量）

代码实战 ：计算 ∫ 0 2 x 2 d x \int_0^2 x^2 dx ∫02x2dx（对应图6的几何意义）

python 复制代码

import sympy as sp

x = sp.symbols('x')
expr = x**2
primitive_func = sp.integrate(expr, x)  # 求原函数
definite_integral = sp.integrate(expr, (x, 0, 2))  # 计算定积分

print(f"原函数: {primitive_func}")
print(f"定积分结果（0到2区间）: {definite_integral}")

执行结果：

复制代码

原函数: x**3/3
定积分结果（0到2区间）: 8/3

6. 常见误区与易错点小结

6.1 导数相关误区

误区1：将"导数为0"等同于"极值点"
纠正：需结合二阶导数或左右导数符号变化判断，例如 f ( x ) = x 3 f(x) = x^3 f(x)=x3在 x = 0 x=0 x=0处导数为0，但非极值点
误区2：忽略导数的定义域限制
纠正：例如 f ( x ) = ln ⁡ x f(x) = \ln x f(x)=lnx的导数为 1 x \frac{1}{x} x1，仅在 x > 0 x>0 x>0时有效

6.2 积分相关误区

误区1：忘记定积分计算中的"常数项抵消"
纠正：原函数的常数项在代入上下限时会相互抵消，无需额外考虑
误区2：混淆"定积分"与"不定积分"的意义
纠正：定积分是具体数值（累积量），不定积分是原函数集合（带常数 C C C）

6.3 跨概念误区

误区：认为"微分和积分互为逆运算"意味着 ∫ f ′ ( x ) d x = f ( x ) \int f'(x) dx = f(x) ∫f′(x)dx=f(x)
纠正：正确关系为 ∫ f ′ ( x ) d x = f ( x ) + C \int f'(x) dx = f(x) + C ∫f′(x)dx=f(x)+C，常数项不可省略

7. 实战拓展：综合应用案例（导数+积分）

7.1 物理场景：匀加速运动的路程计算

已知物体加速度 a ( t ) = 2 m / s 2 a(t) = 2m/s^2 a(t)=2m/s2（恒定），初始速度 v ( 0 ) = 0 v(0) = 0 v(0)=0，初始位置 s ( 0 ) = 0 s(0) = 0 s(0)=0。

由加速度求速度（积分）： v ( t ) = ∫ a ( t ) d t = ∫ 2 d t = 2 t + C v(t) = \int a(t) dt = \int 2 dt = 2t + C v(t)=∫a(t)dt=∫2dt=2t+C，代入 v ( 0 ) = 0 v(0)=0 v(0)=0得 v ( t ) = 2 t v(t)=2t v(t)=2t
由速度求路程（积分）： s ( t ) = ∫ v ( t ) d t = ∫ 2 t d t = t 2 + C s(t) = \int v(t) dt = \int 2t dt = t^2 + C s(t)=∫v(t)dt=∫2tdt=t2+C，代入 s ( 0 ) = 0 s(0)=0 s(0)=0得 s ( t ) = t 2 s(t)=t^2 s(t)=t2
验证： t = 3 s t=3s t=3s时，路程 s ( 3 ) = 9 m s(3)=9m s(3)=9m，与物理公式一致

7.2 经济场景：边际收益的总收益计算

奶茶店边际收益 M R ( x ) = 10 − 0.2 x MR(x) = 10 - 0.2x MR(x)=10−0.2x（ x x x为销量），求销量从0到50杯的总收益。

解：总收益 R = ∫ 0 50 M R ( x ) d x = ∫ 0 50 ( 10 − 0.2 x ) d x = [ 10 x − 0.1 x 2 ] 0 50 = 250 R = \int_0^{50} MR(x) dx = \int_0^{50} (10 - 0.2x) dx = [10x - 0.1x^2]_0^{50} = 250 R=∫050MR(x)dx=∫050(10−0.2x)dx=[10x−0.1x2]050=250元

8. 经典参考书推荐

8.1 数学分析经典

书名	作者	推荐理由
《微积分及其应用》	Marvin L. Bittinger	适合初学者，将微积分与实际应用紧密结合
《微积分入门》	Silvanus P. Thompson	以生活化语言解释微积分，被誉为"微积分的通俗读本"
《深度学习》	Ian Goodfellow, Yoshua Bengio, Aaron Courville	介绍了微积分在深度学习中的应用，适合AI从业者

8.2 实用工具书

书名	作者	推荐理由
《微积分与数学分析精讲》	陈纪修	适合想深入理解微积分原理的读者
《数学之美》	吴军	用生活化的例子解释数学在科技中的应用

9. 结语：微积分------理解变化的艺术

微积分不是抽象的数学符号，而是理解世界变化规律的工具。它帮助我们：

从变化中提取规律
从累积中发现价值
从复杂系统中找到最优解

正如《微积分入门》中所说："微积分是理解变化的艺术，而变化是宇宙的基本法则。"

学习微积分的建议：

从生活实例出发，理解概念

多做练习，巩固计算能力

结合实际应用，加深理解

10. 参考文献

11. 下一篇预告

【数学】【微积分】⑤ 从微积分到人工智能：积分在深度学习中的应用

在下一篇文章中，我们将探讨：

积分在神经网络训练中的应用
概率分布与积分的关系
从连续到离散：微积分在深度学习中的转换
实战案例：用积分优化图像处理算法

敬请期待！

12. 微积分学习路径：从基础到应用的完整旅程

微积分基础
极限与连续
导数与微分
积分与原函数
极限的严格定义
连续函数的性质
无穷小与无穷大
导数的几何意义
基本求导法则
高阶导数
隐函数求导
不定积分
定积分
积分基本定理
积分技巧
ε-δ定义
介值定理
极限运算
瞬时变化率
四则法则
链式法则
乘积法则
曲率计算
基本积分表
定积分几何意义
牛顿-莱布尼茨公式
分部积分
换元积分
应用领域
物理学
经济学
机器学习
工程学
运动学
振动分析
电磁学
边际分析
优化问题
弹性理论
梯度下降
神经网络
损失函数
结构优化
流体动力学
信号处理
高级应用
偏微分方程
数值积分
变分法
傅里叶分析
热传导方程
波动方程
薛定谔方程
辛普森法则
高斯积分
最短路径问题
能量最小化
频谱分析
滤波器设计

12.1 详细学习路径说明（文字版）

🌟 第一阶段：基础概念（1-2周）

概念	关键内容	生活类比	重要性
极限	ε-δ定义、无穷小、极限运算法则	像测量奶茶温度时，越来越接近真实温度	微积分的数学根基
导数	瞬时变化率、几何意义（切线斜率）	自动驾驶汽车的实时速度计算	优化问题的核心
积分	曲线下面积、累积量	从起点到终点的总行驶距离	量化累积效应

💡 学习建议 ：用Python生成函数曲线图（如f(x)=x^2的切线），直观理解导数

🌟 第二阶段：计算法则（2-3周）

法则	公式	应用场景	生活类比
四则法则	(f±g)' = f'±g'	两人合作做蛋糕的总产量	两人同时跑步的总速度
链式法则	(f∘g)' = f'(g)·g'	从奶茶店到家的总时间	乘法法则的复合应用
乘积法则	(fg)' = f'g + fg'	价格和销量共同影响的收入	两人合作做蛋糕的产量
积分技巧	∫u dv = uv - ∫v du	优化奶茶店的利润	分部积分的实用场景

💡 学习建议 ：用Python实现梯度下降算法（如f(x)=x^2的最小值寻找）

🌟 第三阶段：应用领域（3-4周）

领域	核心问题	微积分应用	实际案例
物理学	运动状态变化	速度→加速度→力	自动驾驶的刹车距离计算
经济学	最大化利润	边际成本→最优产量	奶茶店的定价策略优化
机器学习	损失函数最小化	梯度下降算法	AI模型的参数优化
工程学	结构强度分析	应力-应变关系	桥梁设计的承重计算

💡 关键洞察：在机器学习中，80%的优化问题都依赖于导数计算

🌟 第四阶段：高级应用（4周+）

高级主题	数学工具	现代应用	为什么重要
偏微分方程	多元函数导数	气象预测、金融模型	处理多变量系统
数值积分	辛普森法则	计算机图形学	复杂函数的近似计算
变分法	最小作用量原理	机器人路径规划	寻找最优路径
傅里叶分析	积分变换	音频处理、图像压缩	信号的频域分析

💡 学习路径图：从基础概念 → 计算法则 → 应用领域 → 高级主题，层层递进

12.2 推荐学习顺序（附时间规划）

阶段	内容	每日学习时间	重点实践
第1-2周	极限、导数基础	30-45分钟	用Python画函数切线图
第3-4周	导数法则、积分基础	45-60分钟	实现梯度下降算法
第5-6周	物理/经济应用	60分钟	分析奶茶店利润模型
第7-8周	机器学习应用	60-90分钟	用导数优化简单神经网络
第9周+	高级主题	90分钟+	选择1个高级主题深入研究

12.3 学习误区与避坑指南

误区	正确做法	为什么重要
❌ 死记公式	✅ 理解几何意义	导数是切线斜率，不是数字游戏
❌ 只学计算不学应用	✅ 每学一个概念都找实际案例	微积分是工具，不是数学游戏
❌ 跳过基础直接学高级	✅ 严格按路径学习	高级内容建立在基础之上
❌ 不动手写代码	✅ 用Python实现每个概念	理解深度 = 代码实现能力

💡 关键建议 ：每学完一个概念，尝试用代码实现（如用matplotlib画图）

12.4 附：推荐学习资源

资源类型	推荐内容	适合人群	为什么推荐
视频课程	3Blue1Brown《微积分的本质》	初学者	用动画直观解释核心概念
交互式学习	Khan Academy微积分	自学者	互动练习+即时反馈
经典教材	《微积分入门》(Silvanus P. Thompson)	喜欢阅读者	生活化语言解释
实践项目	用导数优化奶茶店利润模型	应用型学习者	从生活场景出发

✨ 终极建议 ：不要追求快速掌握所有内容 ，而是深入理解每个概念，这样才能在实际应用中灵活运用。

12.5 为什么这个学习路径有效？

从直观到抽象：从生活场景（奶茶店、自动驾驶）→ 数学概念 → 高级应用
从计算到应用：先掌握计算方法 → 再理解应用场景
从简单到复杂：逐步增加难度，避免认知过载
从理论到实践：每学一个概念都配实际代码/案例

📌 记住：微积分不是一堆公式，而是理解世界变化规律的工具。当你看到奶茶店的利润曲线时，能想到导数和积分，才是真正的掌握！

13. 往期回顾

【数学】【微积分】① 基础概念与导数的几何意义

【数学】【微积分】② 特殊函数的导数与微分

【数学】【微积分】③ 导数的核心应用

注：本文中所有代码均可在Python 3.8+环境中运行，推荐使用Jupyter Notebook进行学习和实践。

阅读完本文，你将能够：

理解微积分的核心概念
应用导数解决实际问题
了解微积分在现代科技中的应用
为深入学习机器学习打下数学基础

希望这篇文章能帮助你建立对微积分的系统理解，并在实际问题中灵活运用这些工具。数学之美在于其普适性和精确性，而微积分正是这种美的最好体现之一。