微积分中 为什么 dy/dx 有时候拆开,有时候是一个整体?
先说结论再说原因
dydx\frac{dy}{dx}dxdy在导数的时候,是一个整体是不能拆开的。
微分中的dydydy,dxdxdx 与 dydx\frac{dy}{dx}dxdy就不是一回事。
微积分的历史是直观洞察先行,严格逻辑殿后,后面回答了为什么会有像除法的错觉。
1. 导数(derivative)是什么?
导数就是函数变化率的瞬时值,回答的问题是:当自变量 x 稍微变一点点时,函数 y 到底变化多快?
平均变化率
ΔyΔx=f(x+Δx)−f(x)Δx \frac{\Delta y}{\Delta x} = \frac{f(x + \Delta x) - f(x)}{\Delta x} ΔxΔy=Δxf(x+Δx)−f(x)
这叫差商,Δx 是有限的一小段变化,Δy 是对应的函数值变化。这只是平均速度,不是瞬时速度。
导数 = 让 Δx 趋向于 0,取极限

f′(x)=limΔx→0f(x+Δx)−f(x)Δx=limΔx→0ΔyΔx f ^ { \prime } ( x ) = \lim _ { \Delta x \rightarrow 0 } \frac { f ( x + \Delta x ) - f ( x ) } { \Delta x } = \lim _ { \Delta x \rightarrow 0 } \frac { \Delta y } { \Delta x } f′(x)=Δx→0limΔxf(x+Δx)−f(x)=Δx→0limΔxΔy
换个字母
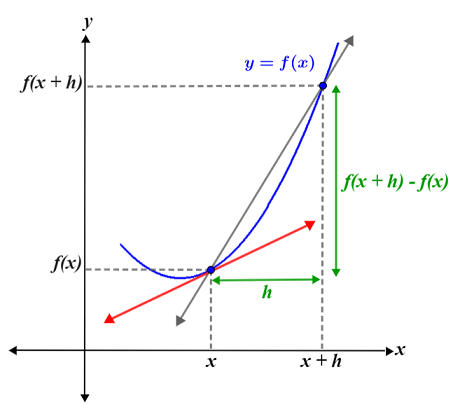
f′(x)=limΔx→0ΔyΔx=limh→0f(x+h)−f(x)h f'(x) = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} f′(x)=Δx→0limΔxΔy=h→0limhf(x+h)−f(x)
这个极限如果存在,就叫 x 处的导数 ,记作:
f′(x)或y′或dydx或dfdx或y˙等 f'(x) \quad 或 \quad y' \quad 或 \quad \frac{dy}{dx} \quad 或 \quad \frac{df}{dx} \quad 或 \quad \dot{y} \quad 等 f′(x)或y′或dxdy或dxdf或y˙等
所以:导数是一个数值(或者函数),表示在某点的瞬时变化率。
2. 微分(differential)是什么?
微分是把很小的一点点变化当成一个近似线性量来看待。
dx:自变量的微小增量(可以看作一个很小的 Δx,但我们把它当成一个 无穷小量 来对待)
dy:函数因 dx 引起的微小变化
公式:
dy=f′(x)⋅dx dy = f'(x) \cdot dx dy=f′(x)⋅dx
这读作"y 的微分 = 导数 × x 的微分
举例:y = x²
导数是 y' = 2x
那么微分就是 dy = 2x dx
dydx\frac{dy}{dx}dxdy(导数)与单独的 dydydy、dxdxdx(微分)绝对不是一回事------前者是描述变化率的整体符号,后者是描述微小变化的独立微分符号,但它们通过微分定义紧密绑定
微分的严格定义 把它们绑定在了一起
第一步:先通过极限定义导数(整体符号):
dydx=f′(x)\frac{dy}{dx} = f'(x)dxdy=f′(x)(是"变化率",和单独的 dydydy、dxdxdx 无关);
第二步:再基于导数定义微分(独立符号):
dy≔f′(x)⋅dxdy \coloneqq f'(x) \cdot dxdy:=f′(x)⋅dx(dydydy 的定义就是"导数×dxdxdx",这里才把 dydydy、dxdxdx 和 dydx\frac{dy}{dx}dxdy 关联起来 ≔\coloneqq:= 表示 "定义为" )
因为莱布尼茨的符号设计太精妙了------他把导数写成"分数形式"dydx\frac{dy}{dx}dxdy,刚好和微分定义 dy=f′(x)dxdy = f'(x)dxdy=f′(x)dx 形成"符号上的除法假象",但这只是"形式巧合",:
当把 dydx=f′(x)\frac{dy}{dx}=f'(x)dxdy=f′(x) 拆成 dy=f′(x)dxdy=f'(x)dxdy=f′(x)dx 时,不是"把分数拆成分子分母相乘",而是"把导数的整体符号,按微分定义转换成微分之间的线性关系";
当用 dydx⋅dxdt=dydt\frac{dy}{dx} \cdot \frac{dx}{dt} = \frac{dy}{dt}dxdy⋅dtdx=dtdy(链式法则)时,不是"约去 dxdxdx",而是"复合函数求导公式的符号表达",结果碰巧和"分数约分"一致。
dy/dx 只是一个整体符号,不能随便拆既然不能随便拆,为什么牛顿、莱布尼茨、欧拉、高斯、柯西......都心安理得地把 dy/dx 当成分数来加减乘除、约分、移项、分离变量?
dy=f′(x) dxdydx=2x⇒dy=2x dx分离变量:dyy=2x dx(微分方程)链式法则:dydx=dydu⋅dudx(可以形式上约分) \begin{align} &dy = f'(x)\,dx \\ &\frac{dy}{dx} = 2x \quad \Rightarrow \quad dy = 2x\,dx \\ &分离变量:\frac{dy}{y} = 2x\,dx \quad(微分方程)\\ &链式法则:\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} \quad(可以形式上约分) \end{align} dy=f′(x)dxdxdy=2x⇒dy=2xdx分离变量:ydy=2xdx(微分方程)链式法则:dxdy=dudy⋅dxdu(可以形式上约分)
为什么dydx\frac{dy}{dx}dxdy不是实数范围内的真除法
1. 先明确:实数范围内真除法a÷ba÷ba÷b(a/ba/ba/b)成立的条件
aaa和bbb是独立的实数 :能单独赋值、独立存在(比如a=5a=5a=5,b=2b=2b=2,不是依赖其他符号的工具性符号);
b≠0b≠0b=0 :除数不能为0(实数范围内,0作除数无意义,比如5/05/05/0不存在);
满足逆运算 :a/b=c ⟺ a=b×ca/b = c \iff a = b×ca/b=c⟺a=b×c(逆运算唯一且成立);
结果唯一 :确定的aaa和bbb(b≠0b≠0b=0)对应唯一的ccc(比如6/2=36/2=36/2=3,只有一个结果)。
2. dx\boldsymbol{dx}dx和dy\boldsymbol{dy}dy不是独立的实数,而是依赖于函数、变量和极限的符号
看到dx = Δx,这里的等于符号的意思是由 Δx 取极限后引入的新符号,代表自变量的微分。
dxdxdx和dydydy的定义是微分,其本质依赖于函数关系、自变量/因变量,以及极限过程:
dxdxdx 源于 Δx\Delta xΔx 取极限后引入的新符号
Δx\Delta xΔx 是自变量的真实有限增量,比如0.10.10.1、0.010.010.01,是有具体数值的变化量;而 dxdxdx 是 Δx→0\Delta x \to 0Δx→0 时抽象出的微分符号,不再是固定的有限数值,而是描述无限趋近于0的微小变化的工具;
dy=f′(x)⋅dxdy = f'(x) \cdot dxdy=f′(x)⋅dxdydydy 是基于导数和 dxdxdx 定义的因变量微分,其含义是yyy 的微小变化量的线性近似,取值依赖于 xxx 和 dxdxdx:xxx 变化时 dydydy 变化,dxdxdx 对应的极限趋势不同时,dydydy 的近似意义也不同,同样不是独立的固定数。
例子:对于y=x2y=x^2y=x2,Δx\Delta xΔx 可以取0.10.10.1、0.0010.0010.001等具体数值,但 dxdxdx 没有固定数值,只是Δx→0\Delta x \to 0Δx→0 过程的符号化表达;dydydy 也会随 xxx 变化(x=2x=2x=2时dy=4dxdy=4dxdy=4dx,x=3x=3x=3时dy=6dxdy=6dxdy=6dx)------不像真除法中的a=5a=5a=5、b=2b=2b=2那样是独立固定的实数,完全不满足真除法中aaa、bbb是独立实数的条件。
3. dydx\boldsymbol{\frac{dy}{dx}}dxdy是导数(变化率),不是两个实数的比值
dydx\frac{dy}{dx}dxdy的严格定义(现代标准分析框架)是极限:
dydx=limΔx→0ΔyΔx\frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}dxdy=Δx→0limΔxΔy
这里的比值是Δy\Delta yΔy(yyy 的真实有限增量)和 Δx\Delta xΔx(xxx 的真实有限增量)的比值,而不是dydydy 和 dxdxdx 的比值;
极限才是重点,dydx\frac{dy}{dx}dxdy 是这个极限的符号记法,本质是xxx 处的瞬时变化率,不是两个实数除法运算的结果。
例子:y=x2y=x^2y=x2的导数是dydx=2x\frac{dy}{dx}=2xdxdy=2x------这个2x2x2x是xxx 处的瞬时变化率,是一个函数:x=2x=2x=2时为444,x=3x=3x=3时为666,随xxx变化而变化,不满足真除法结果唯一的属性。
4. 不满足除法的逆运算(表面满足,本质是特定框架下的定义推导)
表面上看,dydx=f′(x)\frac{dy}{dx}=f'(x)dxdy=f′(x)可以变形为dy=f′(x)⋅dxdy=f'(x) \cdot dxdy=f′(x)⋅dx,看似符合a/b=c ⟹ a=b×ca/b=c \implies a=b×ca/b=c⟹a=b×c的逆运算------但这不是实数除法的逆运算,而是特定数学框架下微分定义的等价关系:
现代标准分析的逻辑:先通过极限定义导数 f′(x)=limΔx→0ΔyΔxf'(x) = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x}f′(x)=Δx→0limΔxΔy,再基于导数定义因变量微分 dy≔f′(x)⋅dxdy \coloneqq f'(x) \cdot dxdy:=f′(x)⋅dx(≔\coloneqq:= 表示定义为);而 dydx=f′(x)\frac{dy}{dx}=f'(x)dxdy=f′(x) 只是这个定义的符号变形整理,不是先有 dy÷dxdy \div dxdy÷dx 的除法,再推导 dy=f′(x)⋅dxdy = f'(x) \cdot dxdy=f′(x)⋅dx。
其他框架例如在莱布尼茨的无穷小框架中,dxdxdx、dydydy 被视为基本无穷小量,dydx\frac{dy}{dx}dxdy 是真的无穷小除法,此时确实是先有除法关系,再将其结果称为导数;非标准分析中,dxdxdx、dydydy 是超实数域中的非零无穷小,除法运算合法,导数就是其比值的标准部分;微分形式中,dxdxdx、dydydy 是流形上的线性泛函,导数通过微分形式的外积、拉回等关系定义,同样不依赖先定义导数再定义微分的顺序。
现代主流教材采用的标准分析中,是因为导数存在,所以定义微分,进而用 dydx\frac{dy}{dx}dxdy 表示导数;而在其他框架中,是因为 dxdxdx、dydydy 作为基本对象存在,所以通过它们的关系得到导数------两种逻辑顺序在各自体系内都自洽,不是完全相反,而是基础对象不同导致的定义顺序差异,但都与实数范围内的除法逆运算无关。
为什么能拆开?------符号变形的合法性与目的
虽然dydx\frac{dy}{dx}dxdy不是实数范围内的真除法,但我们允许符号层面的拆解(比如把dydx=f′(x)\frac{dy}{dx}=f'(x)dxdy=f′(x)拆成dy=f′(x)⋅dxdy=f'(x) \cdot dxdy=f′(x)⋅dx),原因是:
1. 变形的合法性:源于微分的定义,变形后逻辑一致
现代标准分析中,dydydy 的定义本身就是dy=f′(x)⋅dxdy = f'(x) \cdot dxdy=f′(x)⋅dx(基于导数的极限推导,且 dxdxdx 是 Δx→0\Delta x \to 0Δx→0 后的符号),因此 dydx=f′(x)\frac{dy}{dx}=f'(x)dxdy=f′(x) 只是把定义式中的 dxdxdx 从右边移到左边的符号整理,不是除法运算。
其他框架中,拆解的合法性源于自身公理体系(比如无穷小量的除法规则、超实数的运算性质),但本质仍是符号关系的等价表达,而非实数除法。
例子:已知y=x2y=x^2y=x2的导数f′(x)=2xf'(x)=2xf′(x)=2x,根据微分定义,dy=2x⋅dxdy=2x \cdot dxdy=2x⋅dx------这里的dy=2x⋅dxdy=2x \cdot dxdy=2x⋅dx是直接基于导数+微分符号的定义写的,不是用dydx=2x\frac{dy}{dx}=2xdxdy=2x做除法得到的;dxdxdx 虽源于 Δx\Delta xΔx,但此时已成为微分符号,变形只是让线性近似的关系更直观,逻辑完全自洽。
2. 变形的目的是为了计算便利,简化微积分操作
这种符号变形是莱布尼茨符号的优势------虽然本质是极限+符号的组合(或其他框架的基本对象关系),但拆解后能让复杂操作变简单,且不影响结果的正确性:
场景1:快速计算微分近似:比如x=2x=2x=2、Δx=0.001\Delta x=0.001Δx=0.001(对应 dxdxdx 的极限场景)时,直接用dy=2x⋅dx=2×2×0.001=0.004dy=2x \cdot dx=2 \times 2 \times 0.001=0.004dy=2x⋅dx=2×2×0.001=0.004,近似替代真实增量Δy=(2.001)2−22=0.004001\Delta y=(2.001)^2 - 2^2=0.004001Δy=(2.001)2−22=0.004001,不用反复写极限符号,简化计算;
场景2:换元积分(后续应用):比如积分∫2x⋅sin(x2)dx\int 2x \cdot \sin(x^2) dx∫2x⋅sin(x2)dx,令u=x2u=x^2u=x2,则du=2x⋅dxdu=2x \cdot dxdu=2x⋅dx(从dudx=2x\frac{du}{dx}=2xdxdu=2x变形而来,dududu 同样是 Δu→0\Delta u \to 0Δu→0 后的微分符号),积分变成∫sinu du\int \sin u \, du∫sinudu,大幅降低计算难度;
场景3:反函数导数计算:比如y=exy=e^xy=ex(dydx=ex\frac{dy}{dx}=e^xdxdy=ex),反函数x=lnyx=\ln yx=lny,变形得dxdy=1ex=1y\frac{dx}{dy}=\frac{1}{e^x}=\frac{1}{y}dydx=ex1=y1,直接得到反函数的导数,不用重新推导极限表达式。
3. 拆开是符号操作,不是实数运算操作
我们说的拆开,只是把符号dydydy和dxdxdx在等式两边移动,不是把dydydy和dxdxdx当作独立的实数来做除法运算------比如不能说dx=dyf′(x)dx=\frac{dy}{f'(x)}dx=f′(x)dy是dx=dy÷f′(x)dx=dy \div f'(x)dx=dy÷f′(x),而是从dy=f′(x)⋅dxdy=f'(x) \cdot dxdy=f′(x)⋅dx(基于微分定义)推导出来的dxdxdx的符号表达式。
例子:y=2xy=2xy=2x(dydx=2\frac{dy}{dx}=2dxdy=2),变形得dx=dy2dx=\frac{dy}{2}dx=2dy------这里的dx=dy2dx=\frac{dy}{2}dx=2dy表示xxx 的微分与 yyy 的微分在符号意义上满足1:2的线性关系,不是dx=dy÷2dx=dy \div 2dx=dy÷2(因为 dydydy 和 dxdxdx 都没有固定数值,只是 Δy→0\Delta y \to 0Δy→0、Δx→0\Delta x \to 0Δx→0 过程的符号化,是线性近似关系,而非实数除法)。
dydx\frac{dy}{dx}dxdy 是本质为导数的整体符号,形式为分数的便利符号------拆开用是为了高效解题,理解本质时要明确它不是实数除法。
不同数学框架下的区别
| 数学框架 | 基本对象 | 导数与微分的定义顺序 | dydx\frac{dy}{dx}dxdy |
|---|---|---|---|
| 现代标准分析 | 极限(实数序列的收敛) | 先定义导数(极限),再定义微分 dy=f′(x)dxdy = f'(x) dxdy=f′(x)dx | 导数的整体记号,非实数除法 |
| 莱布尼茨无穷小框架 | 无穷小量(直观的无限小) | 先有无穷小量 dxdxdx、dydydy,再定义比值为导数 | 无穷小量的除法结果,是导数的原始含义 |
| 非标准分析 | 超实数(含无穷小、无穷大) | 先定义超实数域的 dxdxdx、dydydy,再定义导数为比值的标准部分 | 超实数的除法(合法),标准部分即为导数 |
为什么会有像除法的错觉(历史原因)?
莱布尼茨发明微积分时,把dxdxdx和dydydy看作无穷小量(一种无限小但不等于0的实数)------那时的dydx\frac{dy}{dx}dxdy是真的无穷小量的除法,所以符号设计成分数形式,方便理解;
但后来发现无穷小量有逻辑矛盾(贝克莱悖论),魏尔斯特拉斯用极限理论重构了微积分:明确 dxdxdx 是 Δx→0\Delta x \to 0Δx→0 时引入的微分符号,dydydy 是基于导数和 dxdxdx 的线性近似符号,两者不再是无穷小实数,dydx\frac{dy}{dx}dxdy 变成了导数的整体符号;
为了兼容莱布尼茨符号的便利性(比如拆解、换元),数学家保留了分数形式和符号变形,但明确了不是实数范围内的真除法------形成了极限+整体符号
整个 18 世纪的微积分全靠有bug的逻辑,推出来的结果全部正确!
虽然 19 世纪的数学家说这不严谨,但他们前仆后继的来修复bug,终于修复好了,发现最后所有结果都一样,只能承认:牛顿和莱布尼茨这套算法不严谨,但结果是对的。莱布尼茨的分数形式符号,恰好与微积分的运算(微分、积分、链式法则)的逻辑一致------虽然现代标准分析中 dydx\frac{dy}{dx}dxdy 是整体符号,但拆开的操作等价于严格的数学推导(如微分定义、积分变量替换、反函数导数公式),相当于跳过繁琐的严格步骤,直接用符号捷径解题,结果自然正确。
| 场景 | 整体写法 | 拆开写法 | 拆开更受欢迎 |
|---|---|---|---|
| 基本微分 | Δy≈f′(x)Δx\Delta y \approx f'(x) \Delta xΔy≈f′(x)Δx(用Δ\DeltaΔ近似) | dy=dydx⋅dxdy = \frac{dy}{dx} \cdot dxdy=dxdy⋅dx | 简洁,方便形式运算 |
| 误差计算 | 相对误差 ≈f′(x)y⋅Δx\approx \frac{f'(x)}{y} \cdot \Delta x≈yf′(x)⋅Δx | dyy=(1y⋅dydx)dx\frac{dy}{y} = \left( \frac{1}{y} \cdot \frac{dy}{dx} \right) dxydy=(y1⋅dxdy)dx | 像分数移项,逻辑直观、容易记忆 |
| 微分方程 | y′=xy ⟹ ∫y dy=∫x dxy' = \frac{x}{y} \implies \int y \, dy = \int x \, dxy′=yx⟹∫ydy=∫xdx(先转换) | y dy=x dxy \, dy = x \, dxydy=xdx(直接拆) | 一步完成分离变量,省略中间转换步骤,效率极高 |
| y=sin(x)y=\sin(x)y=sin(x) | Δy≈cos(x)⋅Δx\Delta y \approx \cos(x) \cdot \Delta xΔy≈cos(x)⋅Δx | dy=cos(x)⋅dxdy = \cos(x) \cdot dxdy=cos(x)⋅dx | 实际应用中高频使用 |
大部分的场景可以放心把 dydx\frac{dy}{dx}dxdy 当成分数拆开/移项/约分**------只要是乘除类操作(如分离变量、换元积分、链式法则、微分近似),结果必然正确;仅少数特殊场景不能滥用,避开即可。
完全可以放心用的场景(附例子,拆了必对)
这些场景的是符号变形等价于严格数学操作,拆开后不仅高效,还不会出错,是大佬们传承下来的解题捷径:
1. 微分近似与误差计算(乘除变形)
操作:从 dydx=f′(x)\frac{dy}{dx}=f'(x)dxdy=f′(x) 拆成 dy=f′(x)dxdy=f'(x)dxdy=f′(x)dx,或 dyy=f′(x)f(x)dx\frac{dy}{y}=\frac{f'(x)}{f(x)}dxydy=f(x)f′(x)dx(相对误差);
原理:本质是微分定义的直接应用,拆开即定义式的变形;
例子:y=x3y=x^3y=x3,求x=2x=2x=2、dx=0.01dx=0.01dx=0.01时的dydydy和相对误差:
拆后计算:dy=3x2dx=3×4×0.01=0.12dy=3x^2dx=3×4×0.01=0.12dy=3x2dx=3×4×0.01=0.12,相对误差dyy=3x2dxx3=3dxx=0.015\frac{dy}{y}=\frac{3x^2dx}{x^3}=\frac{3dx}{x}=0.015ydy=x33x2dx=x3dx=0.015(1.5%);
严格验证:Δy=(2.01)3−23=0.120601\Delta y=(2.01)^3-2^3=0.120601Δy=(2.01)3−23=0.120601,dydydy近似精准,相对误差计算正确。
2. 换元积分(变量替换,场景)
操作:把 dudx=g(x)\frac{du}{dx}=g(x)dxdu=g(x) 拆成 du=g(x)dxdu=g(x)dxdu=g(x)dx,代入积分式简化;
原理:等价于积分变量替换定理,拆开后的微分关系严格对应变量替换逻辑;
例子:计算 ∫2xcos(x2)dx\int 2x\cos(x^2)dx∫2xcos(x2)dx:
拆后操作:令u=x2u=x^2u=x2,则dudx=2x\frac{du}{dx}=2xdxdu=2x,拆成du=2xdxdu=2xdxdu=2xdx,积分变为∫cosudu=sinu+C=sin(x2)+C\int \cos u du=\sin u + C=\sin(x^2)+C∫cosudu=sinu+C=sin(x2)+C;
严格验证:对结果求导,ddxsin(x2)=2xcos(x2)\frac{d}{dx}\sin(x^2)=2x\cos(x^2)dxdsin(x2)=2xcos(x2),与被积函数一致,正确。
3. 分离变量解微分方程(移项+乘除)
操作:把 y′=f(x)g(y)y'=f(x)g(y)y′=f(x)g(y) 拆成 dyg(y)=f(x)dx\frac{dy}{g(y)}=f(x)dxg(y)dy=f(x)dx,再两边积分;
原理:等价于识别导数的微分形式,左边是ddx(∫1g(y)dy)\frac{d}{dx}\left(\int \frac{1}{g(y)}dy\right)dxd(∫g(y)1dy),右边是ddx(∫f(x)dx)\frac{d}{dx}\left(\int f(x)dx\right)dxd(∫f(x)dx);
例子:解 dydx=xy\frac{dy}{dx}=\frac{x}{y}dxdy=yx:
拆后操作:移项得ydy=xdxy dy=x dxydy=xdx,积分∫ydy=∫xdx\int y dy=\int x dx∫ydy=∫xdx,得12y2=12x2+C\frac{1}{2}y^2=\frac{1}{2}x^2+C21y2=21x2+C(即y2=x2+C′y^2=x^2+C'y2=x2+C′);
严格验证:对解求导,2ydydx=2x2y\frac{dy}{dx}=2x2ydxdy=2x,即dydx=xy\frac{dy}{dx}=\frac{x}{y}dxdy=yx,与原方程一致,正确。
4. 链式法则约分(符号简化)
操作:复合函数求导时,dydx=dydu⋅dudx\frac{dy}{dx}=\frac{dy}{du}·\frac{du}{dx}dxdy=dudy⋅dxdu,看似约去dududu;
原理:等价于严格的复合函数求导公式 f′(g(x))⋅g′(x)f'(g(x))·g'(x)f′(g(x))⋅g′(x),约分是符号巧合,结果必然对;
例子:y=sin(x2)y=\sin(x^2)y=sin(x2),令u=x2u=x^2u=x2:
拆后操作:dydx=dydu⋅dudx=cosu⋅2x=2xcos(x2)\frac{dy}{dx}=\frac{dy}{du}·\frac{du}{dx}=\cos u · 2x=2x\cos(x^2)dxdy=dudy⋅dxdu=cosu⋅2x=2xcos(x2);
严格验证:直接求导结果一致,正确。
5. 反函数导数(倒数关系)
操作:若y=f(x)y=f(x)y=f(x),则dxdy=1dydx\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}}dydx=dxdy1,看似倒数(除法逆运算);
原理:等价于反函数导数公式,严格推导可证,拆开后直接用;
例子:y=exy=e^xy=ex(dydx=ex\frac{dy}{dx}=e^xdxdy=ex),反函数x=lnyx=\ln yx=lny:
拆后操作:dxdy=1ex=1y\frac{dx}{dy}=\frac{1}{e^x}=\frac{1}{y}dydx=ex1=y1;
严格验证:直接求导ddylny=1y\frac{d}{dy}\ln y=\frac{1}{y}dydlny=y1,正确。
不能滥用的场景(拆了必错,务必避开)
这些场景的是dydx\frac{dy}{dx}dxdy 是整体导数符号,拆分后破坏其本质,仅3类常见禁忌:
1. 加减运算中拆分(最易出错!)
错误操作:把导数的加减拆成微分的加减除法,比如认为 dy+dzdx=dydx+dzdx\frac{dy+dz}{dx}=\frac{dy}{dx}+\frac{dz}{dx}dxdy+dz=dxdy+dxdz 是拆分------其实这是导数的运算法则,不是a+bc=ac+bc\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}ca+b=ca+cb的除法拆分;更不能反过来,把 dydx+dzdx\frac{dy}{dx}+\frac{dz}{dx}dxdy+dxdz 拆成 dy+dzdx\frac{dy+dz}{dx}dxdy+dz 后再乱移项(比如写成 dy+dz=(y′+z′)dxdy+dz=(y'+z')dxdy+dz=(y′+z′)dx 是对的,但逻辑是导数运算法则,不是除法拆分)。
反例(致命错误):计算 limx→0tanx−sinxx3\lim_{x\to0}\frac{\tan x - \sin x}{x^3}limx→0x3tanx−sinx,若错误拆分等价无穷小的导数:
错:tanx∼x\tan x \sim xtanx∼x(dtanxdx=sec2x\frac{d\tan x}{dx}=\sec^2xdxdtanx=sec2x),sinx∼x\sin x \sim xsinx∼x(dsinxdx=cosx\frac{d\sin x}{dx}=\cos xdxdsinx=cosx),拆成 d(tanx−sinx)dx=sec2x−cosx\frac{d(\tan x - \sin x)}{dx}=\sec^2x - \cos xdxd(tanx−sinx)=sec2x−cosx,再乱代换得 sec2x−cosx3x2\frac{\sec^2x - \cos x}{3x^2}3x2sec2x−cosx(后续计算仍错);
正确做法:先化简函数 tanx−sinx=tanx(1−cosx)\tan x - \sin x = \tan x(1-\cos x)tanx−sinx=tanx(1−cosx),再用等价无穷小替换,而非拆分导数。
2. 高阶导数记号拆分(记号混淆)
错误操作:把二阶导数 d2ydx2\frac{d^2y}{dx^2}dx2d2y 拆成 d2y(dx)2\frac{d^2y}{(dx)^2}(dx)2d2y(甚至写成 dydx⋅1dx\frac{dy}{dx}·\frac{1}{dx}dxdy⋅dx1)------这是完全错误的!
原因:d2ydx2\frac{d^2y}{dx^2}dx2d2y 是整体记号,代表 ddx(dydx)\frac{d}{dx}\left(\frac{dy}{dx}\right)dxd(dxdy)(导数的导数),其中 d2yd^2yd2y 是二阶微分,dx2=(dx)2dx^2=(dx)^2dx2=(dx)2 是自变量微分的平方,但 d2ydx2≠d2y(dx)2\frac{d^2y}{dx^2} \neq \frac{d^2y}{(dx)^2}dx2d2y=(dx)2d2y(二阶微分 d2y=f′′(x)dx2d^2y=f''(x)dx^2d2y=f′′(x)dx2,所以 d2ydx2=f′′(x)\frac{d^2y}{dx^2}=f''(x)dx2d2y=f′′(x),是导数,不是微分的除法)。
3. 多元函数偏导数拆分(记号本质不同)
错误操作:把多元函数的偏导数 ∂y∂x\frac{\partial y}{\partial x}∂x∂y 当成分数拆分------偏导数的 ∂\partial∂ 是偏微分算子,∂y∂x\frac{\partial y}{\partial x}∂x∂y 是整体记号,代表其他变量固定时的变化率,拆分后会破坏固定其他变量的前提。
反例:多元函数 z=x+y2z=x+y^2z=x+y2,偏导数 ∂z∂x=1\frac{\partial z}{\partial x}=1∂x∂z=1,若错误拆分 ∂z=1⋅∂x\partial z = 1·\partial x∂z=1⋅∂x,但忽略了 yyy 变化时 ∂z=2y∂y\partial z = 2y\partial y∂z=2y∂y,单独拆分偏导数会导致变量关系混乱,后续计算(如隐函数偏导)必错。