本文参考RF and Microwave Coupled-Line Circuits
4.2 使用均匀耦合线的方向性耦合器
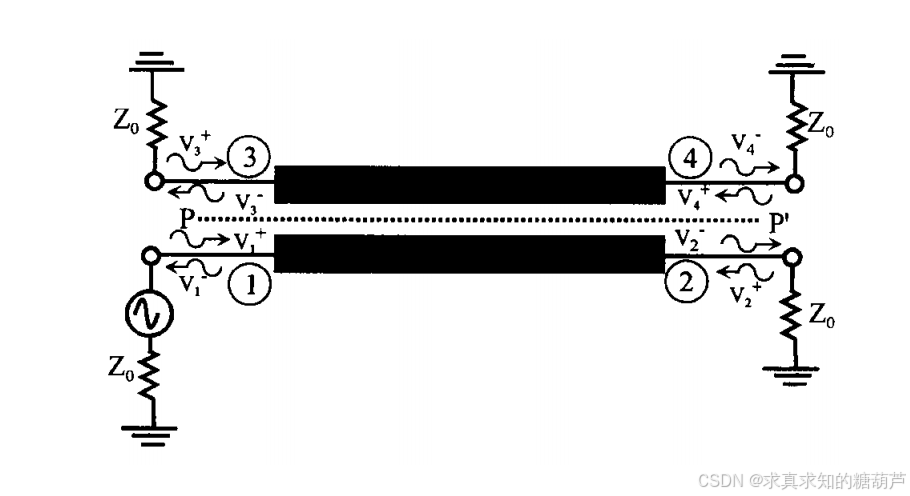
图4.4 由均匀耦合对称线组成的四端口网络。
在阐述了偶模和奇模分析的基本理论之后,我们现在讨论如图4.4所示的、由均匀耦合对称线组成的四端口网络在何种条件下可以充当方向性耦合器。理想方向性耦合器的散射参数在第2章中已讨论过,该章指出,如果四端口网络的所有端口都匹配,则该网络表现为方向性耦合器。由于图4.4所示的网络关于中间平面PP'假设为对称的,端口1和2的匹配自动确保了端口3和4也匹配。因此,条件 S 11 = S 22 = 0 S_{11}=S_{22}=0 S11=S22=0可以让该网络是一个定向耦合器 。用偶模和奇模反射系数表示,散射参数 S 11 S_{11} S11和 S 22 S_{22} S22由(4.22)给出为
S 11 = S 11 e + S 11 o 2 ( 4.23 ) S_{11}=\frac{S_{11e}+S_{11o}}{2}\qquad(4.23) S11=2S11e+S11o(4.23)
S 22 = S 22 e + S 22 o 2 ( 4.24 ) S_{22}=\frac{S_{22e}+S_{22o}}{2}\qquad(4.24) S22=2S22e+S22o(4.24)
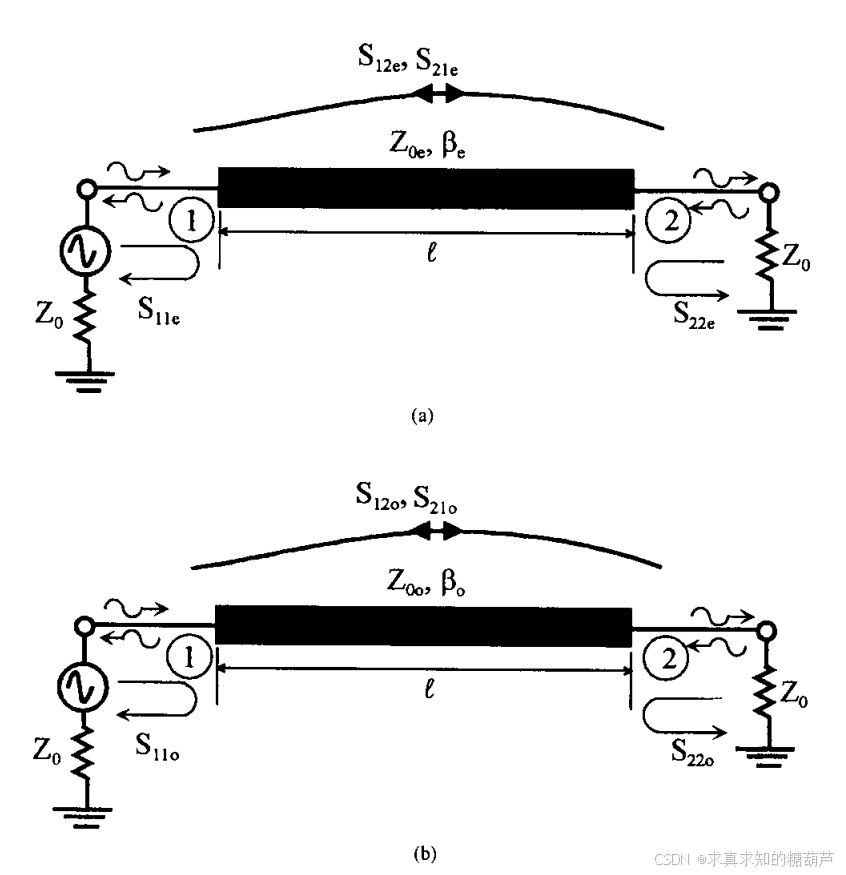
图4.5 用于确定图4.4所示结构的(a)偶模与(b)奇模散射矩阵的等效电路。
用于确定偶模散射参数 S 11 e S_{11e} S11e和 S 22 e S_{22e} S22e的等效电路如图4.5(a)所示,其中 Z 0 e Z_{0e} Z0e和 β e \beta_{e} βe表示对称耦合线的偶模特性和传播常数。类似地,用于确定奇模散射参数 S 11 o S_{11o} S11o和 S 22 o S_{22o} S22o的等效电路如图4.5(b)所示,其中 Z 0 o Z_{0o} Z0o和 β o \beta_{o} βo表示对称耦合线的奇模特性和传播常数。
为了获得 S 11 = S 22 = 0 S_{11}=S_{22}=0 S11=S22=0,这是实现方向性耦合器的条件,存在以下可能性:
情况 I
S 11 e = S 11 o = S 22 e = S 22 o = 0 ( 4.25 ) S_{11e}=S_{11o}=S_{22e}=S_{22o}=0\qquad(4.25) S11e=S11o=S22e=S22o=0(4.25)
当将上述值代入(4.23)和(4.24)时,我们得到 S 11 = S 22 = 0 S_{11}=S_{22}=0 S11=S22=0。此外,使用(4.22),我们得到
S 13 = S 31 = S 42 = S 24 = 0 ( 4.26 ) S_{13}=S_{31}=S_{42}=S_{24}=0\qquad(4.26) S13=S31=S42=S24=0(4.26)
因此,在这种情况下[当满足(4.25)时],没有功率耦合到后向端口。例如,如果功率入射到端口1,则没有功率耦合到耦合线上的端口3。类似地,端口2和4之间没有功率耦合。然而,功率可以在端口1和4之间(或在端口2和3之间)耦合。这类耦合器被称为前向波或同向耦合器,本章将进一步讨论。
情况 II
从(4.23)和(4.24)中,我们看到如果满足以下条件,也可以得到 S 11 = 0 S_{11}=0 S11=0和 S 22 = 0 S_{22}=0 S22=0:
S 11 e = − S 11 o ( 4.27 ) S_{11e}=-S_{11o}\qquad(4.27) S11e=−S11o(4.27)
和
S 22 e = − S 22 o ( 4.28 ) S_{22e}=-S_{22o}\qquad(4.28) S22e=−S22o(4.28)
其中 S 11 e , S 11 o , S 22 e S_{11e},S_{11o},S_{22e} S11e,S11o,S22e和 S 22 o S_{22o} S22o不等于零。使用(4.22),我们然后发现
S 31 ≠ 0 , S 42 ≠ 0 S_{31}\neq 0,S_{42}\neq 0 S31=0,S42=0
在这种情况下,功率因此耦合到后向端口。从方向性耦合器的特性可知,如果 S 31 ≠ 0 S_{31}\neq 0 S31=0,则要么 S 41 = 0 S_{41}=0 S41=0要么 S 21 = 0 S_{21}=0 S21=0。为了确保在耦合线上的前向没有功率耦合,需要满足 S 41 = 0 S_{41}=0 S41=0。使用(4.22),我们发现当满足以下条件时,此条件成立:
S 21 e = S 21 o ( 4.29 ) S_{21e}=S_{21o}\qquad(4.29) S21e=S21o(4.29)
因此,当(4.27)到(4.29)给出的条件成立时,该结构表现为后向波方向性耦合器。
前向后向的区别在于耦合端口的位置 和耦合信号相对于输入信号的传播方向 .前向(同向)耦合器 。耦合信号与主线路中的输入信号同方向 传播。
对前向耦合器来说:信号从端口1输入,大部分功率直接传输到端口2(直通端),同时有一部分功率被耦合到端口4(耦合端),两个端口的信号方向相同。这种定向性通常通过特定的耦合结构(如中提到的双孔波导,其孔间距为λ/4)实现波的干涉。在期望的耦合端口,两个耦合波同相叠加,信号增强;在隔离端口,则反相抵消,理想情况下没有信号输出。
对反向耦合器来说,耦合信号与主线路中的输入信号反方向 传播。信号从端口1输入,但耦合信号却出现在端口3(耦合端),这个端口的信号流向与输入信号相反。在带状线等耦合结构中,能量主要通过**边缘场进行耦合,**这种电磁相互作用的方式天然地导致耦合信号向后传播。
4.2.1 前向波(或同向)方向性耦合器
如前所述,当满足(4.25)时,图4.4所示的四端口网络表现为前向波方向性耦合器。参考图4.5(a, b)分别所示的偶模和奇模等效电路,如果
Z 0 e = Z 0 o = Z 0 Z_{0e}=Z_{0o}=Z_{0} Z0e=Z0o=Z0
则对于耦合段的任何任意长度l,上述条件都满足。在实际中,可以通过保持线之间相对较大的间距来近似满足此条件。将
S 11 e = S 22 e = 0 S_{11e}=S_{22e}=0 S11e=S22e=0
代入以下方程(此方程源于散射矩阵的幺正性):
∣ S 11 e ∣ 2 + ∣ S 21 e ∣ 2 = ∣ S 22 e ∣ 2 + ∣ S 21 e ∣ 2 = 1 |S_{11e}|^{2}+|S_{21e}|^{2}=|S_{22e}|^{2}+|S_{21e}|^{2}=1 ∣S11e∣2+∣S21e∣2=∣S22e∣2+∣S21e∣2=1
我们得到
∣ S 21 e ∣ = 1 |S_{21e}|=1 ∣S21e∣=1全耦合,
或
S 21 e = e − j ψ e ( 4.30 ) S_{21e}=e^{-j\psi_{e}}\qquad(4.30) S21e=e−jψe(4.30)
其中 ψ e \psi_{e} ψe表示偶模信号在端口1和2之间的相位差。类似地,将
S 11 o = S 22 o = 0 S_{11o}=S_{22o}=0 S11o=S22o=0
代入方程
∣ S 11 o ∣ 2 + ∣ S 21 o ∣ 2 = ∣ S 22 o ∣ 2 + ∣ S 21 o ∣ 2 = 1 |S_{11o}|^{2}+|S_{21o}|^{2}=|S_{22o}|^{2}+|S_{21o}|^{2}=1 ∣S11o∣2+∣S21o∣2=∣S22o∣2+∣S21o∣2=1
我们得到
S 21 o = e − j ψ o ( 4.31 ) S_{21o}=e^{-j\psi_{o}}\qquad(4.31) S21o=e−jψo(4.31)
其中 ψ o \psi_{o} ψo表示奇模信号在端口1和2之间的相位差。
由于假设耦合结构是均匀的,我们可以进一步写出
ψ e = β e l ( 4.32 ) \psi_{e}=\beta_{e}l\qquad(4.32) ψe=βel(4.32)
和
ψ o = β o l ( 4.33 ) \psi_{o}=\beta_{o}l\qquad(4.33) ψo=βol(4.33)
其中 β e \beta_{e} βe和 β o \beta_{o} βo分别表示偶模和奇模信号的传播常数,l是耦合段的长度。
此外,使用(4.22),理想前向波方向性耦合器的散射参数由下式给出:
S 11 = S 22 = S 33 = S 44 = 0 ( 4.34 ) S_{11}=S_{22}=S_{33}=S_{44}=0\qquad(4.34) S11=S22=S33=S44=0(4.34)
S 12 = S 21 = S 34 = S 43 = S 21 e + S 21 o 2 = e − j β e l + e − j β o l 2 ( 4.35 ) S_{12}=S_{21}=S_{34}=S_{43}=\frac{S_{21e}+S_{21o}}{2}=\frac{e^{-j\beta_{e}l}+e^{-j\beta_{o}l}}{2}\qquad(4.35) S12=S21=S34=S43=2S21e+S21o=2e−jβel+e−jβol(4.35)
= e − j ( β e + β o ) l 2 cos [ ( β e − β o ) l 2 ] =e^{\frac{-j(\beta_{e}+\beta_{o})l}{2}}\cos\left[\frac{(\beta_{e}-\beta_{o})l}{2}\right] =e2−j(βe+βo)lcos[2(βe−βo)l]
S 14 = S 41 = S 23 = S 32 = S 21 e − S 21 o 2 = e − j β e l − e − j β o l 2 ( 4.36 ) S_{14}=S_{41}=S_{23}=S_{32}=\frac{S_{21e}-S_{21o}}{2}=\frac{e^{-j\beta_{e}l}-e^{-j\beta_{o}l}}{2}\qquad(4.36) S14=S41=S23=S32=2S21e−S21o=2e−jβel−e−jβol(4.36)
= − j e − j ( β e + β o ) l 2 sin [ ( β e − β o ) l 2 ] =-je^{\frac{-j(\beta_{e}+\beta_{o})l}{2}}\sin\left[\frac{(\beta_{e}-\beta_{o})l}{2}\right] =−je2−j(βe+βo)lsin[2(βe−βo)l]
S 13 = S 31 = S 24 = S 42 = 0 ( 4.37 ) S_{13}=S_{31}=S_{24}=S_{42}=0\qquad(4.37) S13=S31=S24=S42=0(4.37)
因此,从端口1耦合到端口4的功率分数为
P 4 P 1 = ∣ S 41 ∣ 2 = sin 2 [ ( β e − β o ) l 2 ] ( 4.38 ) \frac{P_{4}}{P_{1}}=|S_{41}|^{2}=\sin^{2}\left[\frac{(\beta_{e}-\beta_{o})l}{2}\right]\qquad(4.38) P1P4=∣S41∣2=sin2[2(βe−βo)l](4.38)
而从端口1耦合到端口2的功率分数为
P 2 P 1 = ∣ S 21 ∣ 2 = cos 2 [ ( β e − β o ) l 2 ] ( 4.39 ) \frac{P_{2}}{P_{1}}=|S_{21}|^{2}=\cos^{2}\left[\frac{(\beta_{e}-\beta_{o})l}{2}\right]\qquad(4.39) P1P2=∣S21∣2=cos2[2(βe−βo)l](4.39)
注意 ∣ S 21 ∣ 2 + ∣ S 41 ∣ 2 = 1 |S_{21}|^{2}+|S_{41}|^{2}=1 ∣S21∣2+∣S41∣2=1,解释了所有入射功率。显然,**前向波方向性耦合器不能使用TEM模传输线(如同轴线),因为对于TEM模,偶模和奇模的传播常数相等,因此如(4.36)所示,端口1和4之间或端口2和3之间没有耦合。(相速度相等带入值为零)前向波耦合仅存在于非TEM传输线中,如金属波导、鳍线和介质波导,并且在高频率的准TEM模传输线(如微带线)**中也可能存在。在这些传输线结构中,通常偶模和奇模的相速度不相等。
关于前向波或同向耦合器的备注
-
从(4.38)中我们看到,如果方向性耦合器的长度l选择为
l = π ∣ β e − β o ∣ = λ 0 2 ∣ ( ϵ r e e − ϵ r e o ) ∣ ( 4.40 ) l=\frac{\pi}{|\beta_{e}-\beta_{o}|}=\frac{\lambda_{0}}{2|(\sqrt{\epsilon_{ree}}-\sqrt{\epsilon_{reo}})|}\qquad(4.40) l=∣βe−βo∣π=2∣(ϵree −ϵreo )∣λ0(4.40)
则可以在线之间实现完全的功率传输。这个结果意义重大,意味着即使偶模和奇模传播常数的差值任意小,只要根据(4.40)选择耦合器的长度,就可以在线之间实现完全的功率传输。我们稍后将证明,在后向波方向性耦合器的情况下,不可能完全地将功率从一条线传输到另一条线。
-
通过比较(4.35)和(4.36),我们发现 S 41 S_{41} S41和 S 21 S_{21} S21之间的相位差是90度。"耦合"线上的波因此与"直通"波有90度的相位差。
-
在推导前向波耦合方程时,我们假设了(4.25) S 11 e = S 11 o = S 22 e = S 22 o = 0 S_{11e}=S_{11o}=S_{22e}=S_{22o}=0 S11e=S11o=S22e=S22o=0给出的条件得到满足,这导致端口1和3之间或端口2和4之间的耦合为零。因此,耦合器的方向性和隔离度是无限的。然而,**通常上述条件不能完全满足。因此,耦合线之间总是存在一定量(无论多小)的后向波耦合。**如果已知 S 11 e , S 11 o , S 22 e S_{11e},S_{11o},S_{22e} S11e,S11o,S22e和 S 22 o S_{22o} S22o的值,则可以使用(4.22)确定后向波耦合( S 31 S_{31} S31和 S 42 S_{42} S42)的确切量。
4.2.2 后向波方向性耦合器
如前所述,如果满足以下条件,图4.4所示的对称四端口网络表现为后向波方向性耦合器:
S 11 o = − S 11 e S_{11o}=-S_{11e} S11o=−S11e
S 22 o = − S 22 e S_{22o}=-S_{22e} S22o=−S22e
和
S 21 o = S 21 e S_{21o}=S_{21e} S21o=S21e
其中 S 11 o , S 11 e , S 22 o S_{11o},S_{11e},S_{22o} S11o,S11e,S22o和 S 22 e S_{22e} S22e不等于零。如果耦合线是TEM类型的(类似于带状线),并且线的偶模和奇模特性阻抗选择得当,则上述条件很容易满足。偶模和奇模的等效电路分别如图4.5(a)和4.5(b)所示。使用这些等效电路,可以确定耦合器偶模和奇模的ABCD矩阵。例如,使用表2.2,偶模和奇模的ABCD矩阵分别由下式给出:
A e B e C e D e \] = \[ cos ( β l ) j Z 0 e sin ( β l ) j sin ( β l ) Z 0 e cos ( β l ) \] ( 4.41 ) \\begin{bmatrix}A_{e}\&B_{e}\\\\C_{e}\&D_{e}\\end{bmatrix}=\\begin{bmatrix}\\cos(\\beta l)\&jZ_{0e}\\sin(\\beta l)\\\\\\frac{j\\sin(\\beta l)}{Z_{0e}}\&\\cos(\\beta l)\\end{bmatrix}\\qquad(4.41) \[AeCeBeDe\]=\[cos(βl)Z0ejsin(βl)jZ0esin(βl)cos(βl)\](4.41) 和 \[ A o B o C o D o \] = \[ cos ( β l ) j Z 0 o sin ( β l ) j sin ( β l ) Z 0 o cos ( β l ) \] ( 4.42 ) \\begin{bmatrix}A_{o}\&B_{o}\\\\C_{o}\&D_{o}\\end{bmatrix}=\\begin{bmatrix}\\cos(\\beta l)\&jZ_{0o}\\sin(\\beta l)\\\\\\frac{j\\sin(\\beta l)}{Z_{0o}}\&\\cos(\\beta l)\\end{bmatrix}\\qquad(4.42) \[AoCoBoDo\]=\[cos(βl)Z0ojsin(βl)jZ0osin(βl)cos(βl)\](4.42) 其中我们假设偶模和奇模的传播常数相同,并用 β \\beta β表示。由于耦合线端接在阻抗 Z 0 Z_{0} Z0上,从(2.98)和(2.99)可以证明偶模和奇模反射系数为(**参考阻抗为 Z 0 Z_0 Z0** ):  S 11 e = S 22 e = j ( Z 0 e Z 0 − Z 0 Z 0 e ) sin β l 2 cos β l + j ( Z 0 e Z 0 + Z 0 Z 0 e ) sin β l ( 4.43 ) S_{11e}=S_{22e}=\\frac{j(\\frac{Z_{0e}}{Z_{0}}-\\frac{Z_{0}}{Z_{0e}})\\sin\\beta l}{2\\cos\\beta l+j(\\frac{Z_{0e}}{Z_{0}}+\\frac{Z_{0}}{Z_{0e}})\\sin\\beta l}\\qquad(4.43) S11e=S22e=2cosβl+j(Z0Z0e+Z0eZ0)sinβlj(Z0Z0e−Z0eZ0)sinβl(4.43) 和 S 11 o = S 22 o = j ( Z 0 o Z 0 − Z 0 Z 0 o ) sin β l 2 cos β l + j ( Z 0 o Z 0 + Z 0 Z 0 o ) sin β l ( 4.44 ) S_{11o}=S_{22o}=\\frac{j(\\frac{Z_{0o}}{Z_{0}}-\\frac{Z_{0}}{Z_{0o}})\\sin\\beta l}{2\\cos\\beta l+j(\\frac{Z_{0o}}{Z_{0}}+\\frac{Z_{0}}{Z_{0o}})\\sin\\beta l}\\qquad(4.44) S11o=S22o=2cosβl+j(Z0Z0o+Z0oZ0)sinβlj(Z0Z0o−Z0oZ0)sinβl(4.44) 比较(4.43)和(4.44),我们发现当 Z 0 e Z 0 = Z 0 Z 0 o \\frac{Z_{0e}}{Z_{0}}=\\frac{Z_{0}}{Z_{0o}} Z0Z0e=Z0oZ0 或 Z 0 e Z 0 o = Z 0 2 ( 4.45 ) Z_{0e}Z_{0o}=Z_{0}\^{2}\\qquad(4.45) Z0eZ0o=Z02(4.45) 时,**对于任何任意的长度l值,条件 S 11 e = − S 11 o S_{11e}=-S_{11o} S11e=−S11o和 S 22 e = − S 22 o S_{22e}=-S_{22o} S22e=−S22o都满足。** 散射参数 S 21 o S_{21o} S21o和 S 21 e S_{21e} S21e可以从(2.100)计算如下: S 21 e = 2 2 cos β l + j ( Z 0 e Z 0 + Z 0 Z 0 e ) sin β l ( 4.46 ) S_{21e}=\\frac{2}{2\\cos{\\beta l}+j(\\frac{Z_{0e}}{Z_{0}}+\\frac{Z_{0}}{Z_{0e}})\\sin{\\beta l}}\\qquad(4.46) S21e=2cosβl+j(Z0Z0e+Z0eZ0)sinβl2(4.46) 和 S 21 o = 2 2 cos β l + j ( Z 0 o Z 0 + Z 0 Z 0 o ) sin β l ( 4.47 ) S_{21o}=\\frac{2}{2\\cos{\\beta l}+j(\\frac{Z_{0o}}{Z_{0}}+\\frac{Z_{0}}{Z_{0o}})\\sin{\\beta l}}\\qquad(4.47) S21o=2cosβl+j(Z0Z0o+Z0oZ0)sinβl2(4.47) 我们看到当(4.45)成立时, S 21 e = S 21 o S_{21e}=S_{21o} S21e=S21o,如(4.29)所要求。因此,**(4.45)给出了TEM后向波方向性耦合器的必要条件。**一旦知道 S 11 o , S 11 e , S 21 o , S 21 e S_{11o},S_{11e},S_{21o},S_{21e} S11o,S11e,S21o,S21e的值,就可以使用(4.22)轻松确定理想后向波方向性耦合器的散射参数,如下所示: S 11 = S 22 = S 33 = S 44 = 0 ( 4.48 ) S_{11}=S_{22}=S_{33}=S_{44}=0\\qquad(4.48) S11=S22=S33=S44=0(4.48) S 14 = S 41 = S 23 = S 32 = 0 ( 4.49 ) S_{14}=S_{41}=S_{23}=S_{32}=0\\qquad(4.49) S14=S41=S23=S32=0(4.49) S 12 = S 21 = S 34 = S 43 = S 21 e + S 21 o 2 = S 21 e = S 21 o ( 4.50 ) S_{12}=S_{21}=S_{34}=S_{43}=\\frac{S_{21e}+S_{21o}}{2}=S_{21e}=S_{21o}\\qquad(4.50) S12=S21=S34=S43=2S21e+S21o=S21e=S21o(4.50) = 2 2 cos β l + j ( Z 0 e Z 0 + Z 0 o Z 0 ) sin β l =\\frac{2}{2\\cos{\\beta l}+j(\\frac{Z_{0e}}{Z_{0}}+\\frac{Z_{0o}}{Z_{0}})\\sin{\\beta l}} =2cosβl+j(Z0Z0e+Z0Z0o)sinβl2 S 13 = S 31 = S 24 = S 42 = S 11 e − S 11 o 2 = S 11 e = − S 11 o ( 4.51 ) S_{13}=S_{31}=S_{24}=S_{42}=\\frac{S_{11e}-S_{11o}}{2}=S_{11e}=-S_{11o}\\qquad(4.51) S13=S31=S24=S42=2S11e−S11o=S11e=−S11o(4.51) = j ( Z 0 e Z 0 − Z 0 o Z 0 ) sin β l 2 cos β l + j ( Z 0 e Z 0 + Z 0 o Z 0 ) sin β l =\\frac{j(\\frac{Z_{0e}}{Z_{0}}-\\frac{Z_{0o}}{Z_{0}})\\sin\\beta l}{2\\cos{\\beta l}+j(\\frac{Z_{0e}}{Z_{0}}+\\frac{Z_{0o}}{Z_{0}})\\sin{\\beta l}} =2cosβl+j(Z0Z0e+Z0Z0o)sinβlj(Z0Z0e−Z0Z0o)sinβl 从(4.45)和(4.50),我们得到 S 21 = 1 − k 2 1 − k 2 cos θ + j sin θ ( 4.52 ) S_{21}=\\frac{\\sqrt{1-k\^{2}}}{\\sqrt{1-k\^{2}}\\cos{\\theta}+j\\sin{\\theta}}\\qquad(4.52) S21=1−k2 cosθ+jsinθ1−k2 (4.52) 此外,从(4.45)和(4.51), S 31 = j k sin θ 1 − k 2 cos θ + j sin θ ( 4.53 ) S_{31}=\\frac{jk\\sin\\theta}{\\sqrt{1-k\^{2}}\\cos\\theta+j\\sin\\theta}\\qquad(4.53) S31=1−k2 cosθ+jsinθjksinθ(4.53) 其中 θ = β l \\theta=\\beta l θ=βl,且 k = Z 0 e − Z 0 o Z 0 e + Z 0 o ( 4.54 ) k=\\frac{Z_{0e}-Z_{0o}}{Z_{0e}+Z_{0o}}\\qquad(4.54) k=Z0e+Z0oZ0e−Z0o(4.54) **端口1和3之间(或端口2和4之间)的最大耦合量出现在** θ = β l = π 2 r a d s ( 4.55 ) \\theta=\\beta l=\\frac{\\pi}{2}\\,rads\\qquad(4.55) θ=βl=2πrads(4.55) 或 l = π 2 β = λ g 4 l=\\frac{\\pi}{2\\beta}=\\frac{\\lambda_{g}}{4} l=2βπ=4λg 时,其中 λ g \\lambda_{g} λg表示传输线介质中的导波波长。将 θ = π / 2 \\theta=\\pi/2 θ=π/2代入(4.53)可找到耦合的最大值,得到 ∣ S 13 ∣ = ∣ S 31 ∣ = ∣ S 24 ∣ = ∣ S 42 ∣ = k ( 4.56 ) \|S_{13}\|=\|S_{31}\|=\|S_{24}\|=\|S_{42}\|=k\\qquad(4.56) ∣S13∣=∣S31∣=∣S24∣=∣S42∣=k(4.56) 此外,当 θ = π / 2 \\theta=\\pi/2 θ=π/2时, ∣ S 12 ∣ = ∣ S 21 ∣ = ∣ S 34 ∣ = ∣ S 43 ∣ = 1 − k 2 ( 4.57 ) \|S_{12}\|=\|S_{21}\|=\|S_{34}\|=\|S_{43}\|=\\sqrt{1-k\^{2}}\\qquad(4.57) ∣S12∣=∣S21∣=∣S34∣=∣S43∣=1−k2 (4.57) 因此,在 θ = β l = π / 2 \\theta=\\beta l=\\pi/2 θ=βl=π/2的频率处,后向波耦合器的散射矩阵可以表示如下: \[ S \] = \[ 0 − j 1 − k 2 k 0 − j 1 − k 2 0 0 k k 0 0 − j 1 − k 2 0 k − j 1 − k 2 0 \] ( 4.58 ) \[S\]=\\begin{bmatrix}0\&-j\\sqrt{1-k\^{2}}\&k\&0\\\\-j\\sqrt{1-k\^{2}}\&0\&0\&k\\\\k\&0\&0\&-j\\sqrt{1-k\^{2}}\\\\0\&k\&-j\\sqrt{1-k\^{2}}\&0\\end{bmatrix}\\qquad(4.58) \[S\]= 0−j1−k2 k0−j1−k2 00kk00−j1−k2 0k−j1−k2 0 (4.58) 此散射矩阵在耦合器长度为四分之一波长的频率处有效。然而,我们可以使用(4.48)、(4.49)、(4.52)和(4.53)计算后向波耦合器在任何其他频率的频率响应。各种耦合值的理想后向波耦合器的频率响应在第6章给出。 **从(4.45)和(4.54)中,偶模和奇模特性阻抗与电压耦合系数 k k k之间的关系推导如下:** k = Z 0 e − Z 0 o Z 0 e + Z 0 o ( 4.54 ) k=\\frac{Z_{0e}-Z_{0o}}{Z_{0e}+Z_{0o}}\\qquad(4.54) k=Z0e+Z0oZ0e−Z0o(4.54) Z 0 e Z 0 o = Z 0 2 ( 4.45 ) Z_{0e}Z_{0o}=Z_{0}\^{2}\\qquad(4.45) Z0eZ0o=Z02(4.45) 由式(4.54)可得: k ( Z 0 e + Z 0 o ) = Z 0 e − Z 0 o k(Z_{0e} + Z_{0o}) = Z_{0e} - Z_{0o} k(Z0e+Z0o)=Z0e−Z0o 整理得: Z 0 e Z 0 o = k + 1 1 − k = Z 0 e = Z 0 o ⋅ 1 + k 1 − k ( A ) \\frac{Z_{0e}}{Z_{0o}} = \\frac{k + 1}{1 - k}= Z_{0e} = Z_{0o} \\cdot \\frac{1 + k}{1 - k} \\qquad (A) Z0oZ0e=1−kk+1=Z0e=Z0o⋅1−k1+k(A) 将式(A)代入式(4.45): ( Z 0 o ⋅ 1 + k 1 − k ) ⋅ Z 0 o = Z 0 2 \\left( Z_{0o} \\cdot \\frac{1 + k}{1 - k} \\right) \\cdot Z_{0o} = Z_0\^2 (Z0o⋅1−k1+k)⋅Z0o=Z02 Z 0 o 2 ⋅ 1 + k 1 − k = Z 0 2 Z_{0o}\^2 \\cdot \\frac{1 + k}{1 - k} = Z_0\^2 Z0o2⋅1−k1+k=Z02 解得: Z 0 o 2 = Z 0 2 ⋅ 1 − k 1 + k Z_{0o}\^2 = Z_0\^2 \\cdot \\frac{1 - k}{1 + k} Z0o2=Z02⋅1+k1−k 因此: Z 0 o = Z 0 1 − k 1 + k ( 4.59 a ) Z_{0o} = Z_0 \\sqrt{\\frac{1 - k}{1 + k}} \\qquad (4.59a) Z0o=Z01+k1−k (4.59a) 同理,由式(A)解出 Z 0 o = Z 0 e ⋅ 1 − k 1 + k Z_{0o} = Z_{0e} \\cdot \\frac{1 - k}{1 + k} Z0o=Z0e⋅1+k1−k,代入式(4.45): Z 0 e ⋅ ( Z 0 e ⋅ 1 − k 1 + k ) = Z 0 2 Z_{0e} \\cdot \\left( Z_{0e} \\cdot \\frac{1 - k}{1 + k} \\right) = Z_0\^2 Z0e⋅(Z0e⋅1+k1−k)=Z02 Z 0 e 2 ⋅ 1 − k 1 + k = Z 0 2 Z_{0e}\^2 \\cdot \\frac{1 - k}{1 + k} = Z_0\^2 Z0e2⋅1+k1−k=Z02 解得: Z 0 e 2 = Z 0 2 ⋅ 1 + k 1 − k ( 4.59 b ) Z_{0e}\^2 = Z_0\^2 \\cdot \\frac{1 + k}{1 - k}\\qquad(4.59b) Z0e2=Z02⋅1−k1+k(4.59b) 小结一下 Z 0 o = Z 0 1 − k 1 + k ( 4.59 a ) Z_{0o}=Z_{0}\\sqrt{\\frac{1-k}{1+k}} \\qquad(4.59a) Z0o=Z01+k1−k (4.59a) Z 0 e = Z 0 1 + k 1 − k ( 4.59 b ) Z_{0e}=Z_{0}\\sqrt{\\frac{1+k}{1-k}} \\qquad(4.59b) Z0e=Z01−k1+k (4.59b) ### 例4.1 计算一个20分贝、四分之一波长、50欧姆的后向波耦合器的偶模和奇模特性阻抗。 对于一个20分贝的耦合器, k = 10 − 20 / 20 = 0.1 k=10\^{-20/20}=0.1 k=10−20/20=0.1。给定终端阻抗为50欧姆,则从(4.59)得, Z 0 e = 55.3 Z_{0e}=55.3 Z0e=55.3欧姆, Z 0 o = 45.2 Z_{0o}=45.2 Z0o=45.2欧姆。 ### 用电容参数表示的耦合系数k 偶模与奇模电容和阻抗之间的关系如下 C a = C b = Q e V e = C e ( 3.41 ) C_{a}=C_{b}=\\frac{Q_{e}}{V_{e}}=C_{e} \\qquad (3.41) Ca=Cb=VeQe=Ce(3.41) Q o = ( C a + 2 C m ) V o ( 3.42 ) Q_{o}=(C_{a}+2C_{m})V_{o} \\quad (3.42) Qo=(Ca+2Cm)Vo(3.42) C a + 2 C m = Q o V o = C o ( 3.43 ) C_{a}+2C_{m}=\\frac{Q_{o}}{V_{o}}=C_{o} \\quad (3.43) Ca+2Cm=VoQo=Co(3.43) Z 0 e = 1 v p e C e = ω β e C e ( 3.45 ) Z_{0e} = \\frac{1}{v_{pe}C_{e}} = \\frac{\\omega}{\\beta_{e}C_{e}} \\quad (3.45) Z0e=vpeCe1=βeCeω(3.45) Z 0 o = 1 v p o C o = ω β o C o ( 3.46 ) Z_{0o} = \\frac{1}{v_{po}C_{o}} = \\frac{\\omega}{\\beta_{o}C_{o}} \\quad (3.46) Z0o=vpoCo1=βoCoω(3.46) k = Z 0 e − Z 0 o Z 0 e + Z 0 o ( 4.54 ) k=\\frac{Z_{0e}-Z_{0o}}{Z_{0e}+Z_{0o}}\\qquad(4.54) k=Z0e+Z0oZ0e−Z0o(4.54) 分别从(3.45)和(3.46)代入 Z 0 e Z_{0e} Z0e和 Z 0 o Z_{0o} Z0o的值,并与(3.41)和(3.43)一起代入(4.54),我们得到 k = C m C a + C m ( 4.60 ) k=\\frac{C_{m}}{C_{a}+C_{m}}\\qquad(4.60) k=Ca+CmCm(4.60) **其中 C a C_{a} Ca(平板电容)和 C m C_{m} Cm(互电容)表示如图3.5所示的耦合线的电容( C b = C a C_{b}=C_{a} Cb=Ca)** 。 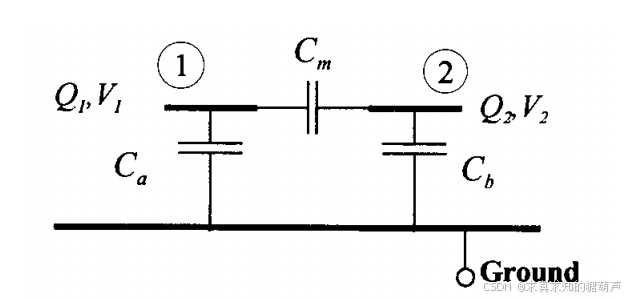 图3.5 耦合线路电容示意图 ### 关于后向波方向性耦合器的备注 1. **方程(4.53)表明,两条耦合线之间可以实现的后向波耦合存在一个最大值。由(4.56)给出的最大耦合值出现在耦合器长度为四分之一波长(或其奇数倍)时。**这不同于对称前向波方向性耦合器的情况,在前者中,通过适当选择耦合段的长度,可以在线之间实现任意耦合(从0-1)。 2. 通过比较(4.52)和(4.53),我们发现**耦合到"后向"端口( S 31 S_{31} S31)的波与耦合到"直通"端口( S 21 S_{21} S21)的波相位差为90度。这种关系与耦合段的电长度无关。因此,这类耦合器能够在很宽的频率范围内用作正交移相器。**