目录
【611.有效三角形个数】
1、题目描述

2、实现核心及思路
构成三角形的条件:设三角形三边长分别为a(最长边),b(最短边),c。
则有 a + b > c。
通过对三角形三边关系的分析,问题就是怎样找到三角形的最长边和最短边。解决这个问题:
我们可以先将数组元素进行排序(升序),让其满足单调性。每次固定最大值为第三边,最左边元素作为最短边,次最大值作为最长边,让最短边和最长边求和并与第三边比较。
解题步骤:
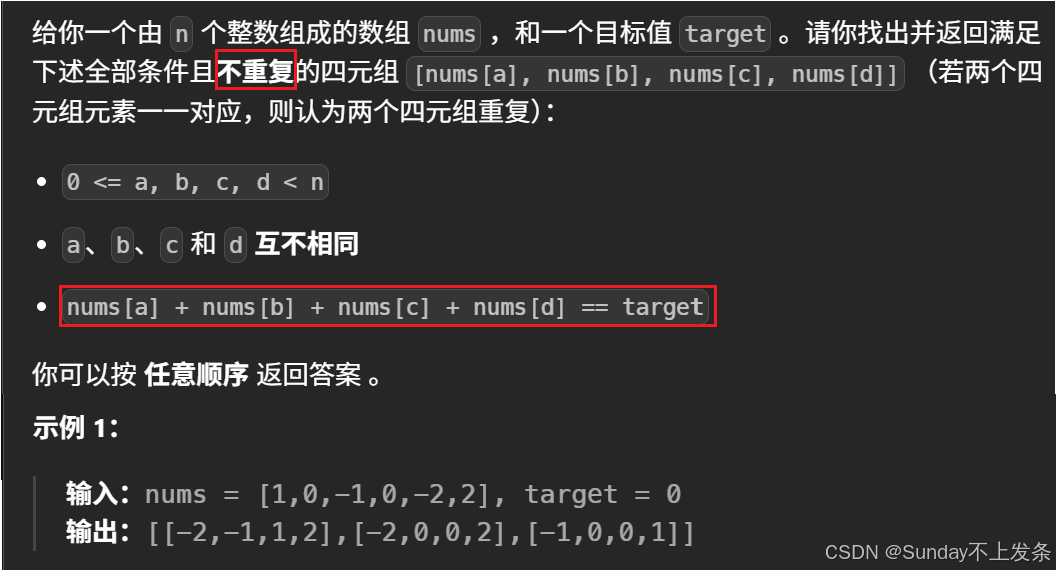
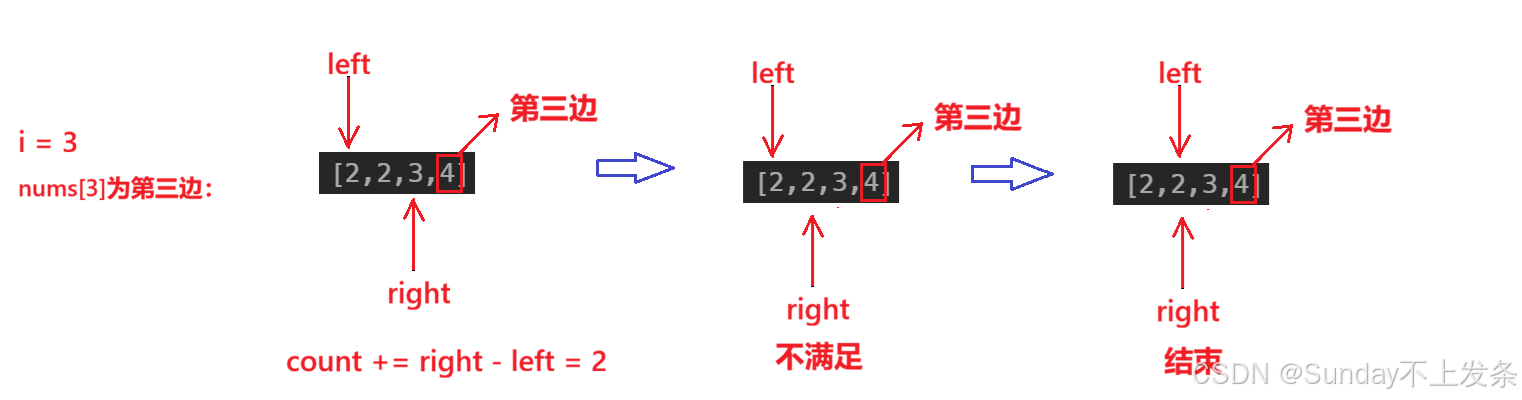
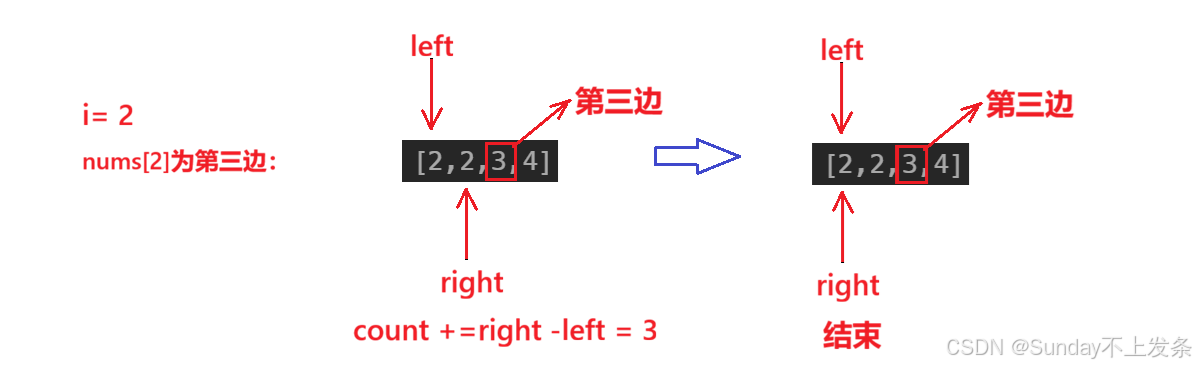
(1)排序(升序),降序也可。
(2)从右往左将数组元素依次作为第三边;让左指针 left 指向最左侧元素,作为最短边;右指针 right 指向第三边左侧第一个元素,作为最长边。
++注意:++由于需要三个边构成三角形,则第三边最多为数组的第三个元素(nums[2])。
(3)最短边与最长边求和并与第三边比较。
++注意:++
**•**由于已经按照升序排序,只要 nums[left] + nums[right] > 第三边,说明只要将左侧元素作为最短边均满足要求,则此时有满足要求的 right - left 个三角形(更新结果) , 然后
right--,因为nums[left] + nums[right--] 仍有可能满足要求;
•如果nums[left] + nums[right] <= 第三边,则只有让left++,才有可能让最短边与最长边之和大于第三边(right--只能让两者之和更小)。
***结束条件:***right >= left。
思路可视化:
代码实现:
cpp
class Solution {
public:
int triangleNumber(vector<int>& nums)
{
sort(nums.begin(),nums.end()); // 升序排序
int count = 0; // 记录三角形个数
// 从右往左依次将最大值作为第三边
for(int i = nums.size()-1;i >= 2;i--)
{
int left = 0; // 左指针(最短边)
int right = i-1; // 右指针(最长边)
while(left < right)
{
if(nums[left] + nums[right] > nums[i]) // 两边之和大于第三边
{
count += right-left; // 更新结果
right--; // 寻找其他可能结果
}
else left++; // 寻找与最长边相加可能大于第三边的最短边
}
}
return count;
}
};【179.查找总价格为目标值的两个商品】
1、题目描述:

2、实现核心及思路:
实际就是求两数之和满足目标值,暴力算法非常简单,但可能超时。
与上一题类似我们也是结合单调性与双指针求解:
(1)排序(默认升序),但注意数组可能已经有序(本题已经为升序数组)。
(2)让左指针 left 指向最左边元素(最小值),右指针 right 指向最右边元素(最大值)。
(3)两数求和,并与目标值比较:
•****和小于目标值,left++,只有这样才可能让和等于目标值(right-- 只能使得和更小);
•****和大于目标值,right--,只有这样才有可能让和等于目标值(left++ 只能使得和更大);
(4)输出结果。
代码实现:
cpp
class Solution {
public:
vector<int> twoSum(vector<int>& price, int target)
{
int left = 0, right = price.size() - 1;
while(left < right)
{
if(price[left] + price[right] < target) left++;
else if(price[left] + price[right] > target) right--;
else break;
}
return {price[left], price[right]};
}
};【15.三数之和】
1、题目描述:

2、实现核心及思路:
要 求满足要求的三数之和,我们可以这样处理:nums[ i ] + nums[ j ] + nums[ k ] = 0,即
nums[ i ] + nums[ j ] = -nums[ k ],我们可以将 -nums[ k ]作为 target,这样就转化为了求两数之和的问题。
解题步骤:
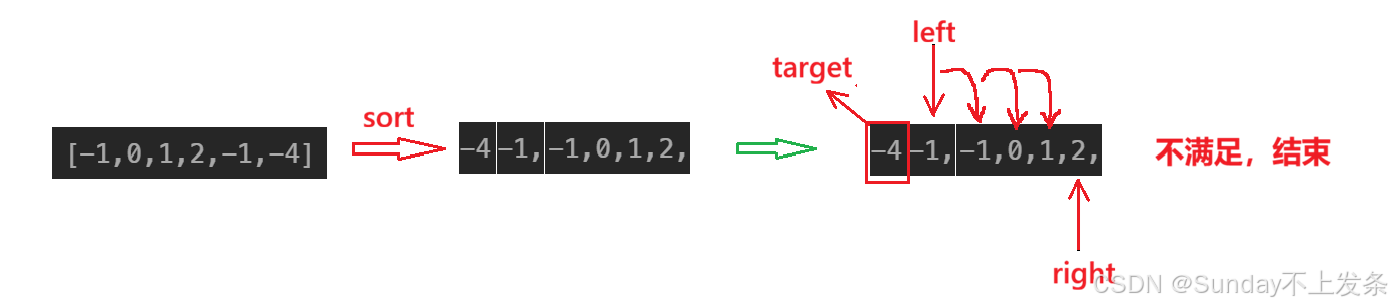
(1)排序(默认升序);
(2)从左往右依次固定一个元素作为 target,并让左指针 left 指向value 左侧元素;右指针 right 指向最右边元素。当 nums[ left ] + nums[ right ] = -target 时,即此三数满足要求(更新结果);
• 若和小于目标值(-target**),left++**,只有这样才可能让和等于目标值(right-- 只能使得和更小);
• 若****和大于目标值(-target),right--,只有这样才有可能让和等于目标值(left++ 只能使得和更大);
**•**更新结果,让left++,right--,继续找。
**循环条件:left < right。
++注意:++ 最后结果不可重复,所以需要去重:**• 方法一:**而由于数组元素升序排序的原因,对于重复的结果,其顺序也相同。所以,我们可以用 set<vector<int>> 来存储结果(set可以去重)。
**• 方法二:**当更新完结果后让左指针 left 和右指针 right 跳过相同的值;同时,在固定目标值时也需要跳过相同的值。
++💥技巧:++ 由于我们按照升序排序,即单调递增,当我们固定的target > 0(为正)时,往右所有的数肯定都已经大于0了,就不用找了。
思路可视化:
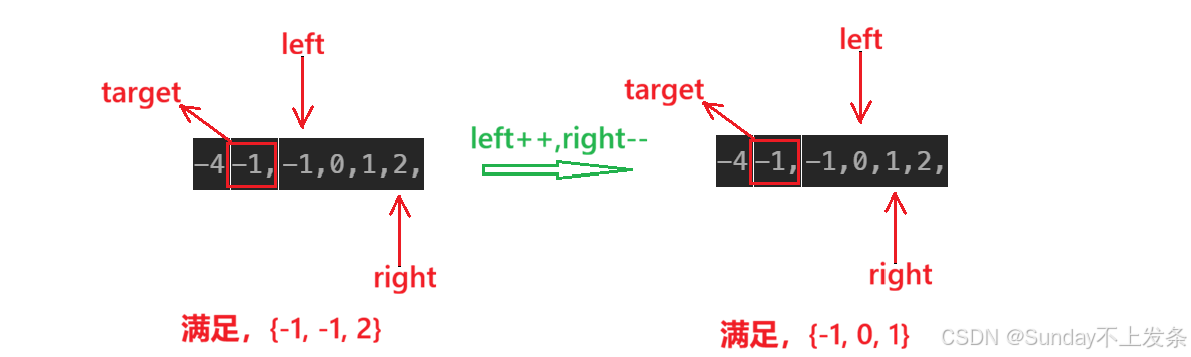
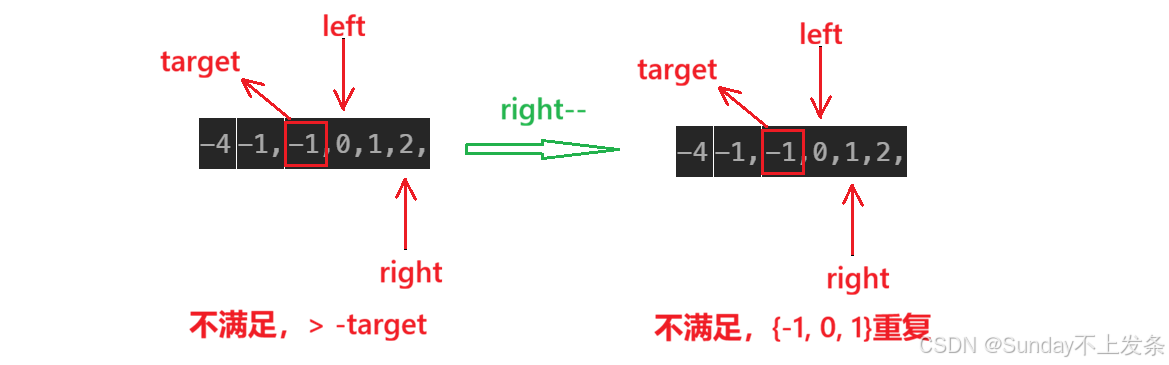
代码实现:
cpp
class Solution
{
public:
vector<vector<int>> threeSum(vector<int>& nums)
{
sort(nums.begin(), nums.end()); // 排序
vector<vector<int>> ret; // 存储结果
// 从左往右依次固定元素为target
for(int i = 0; i < nums.size() - 2;)
{
int target = nums[i]; // 目标值
int left = i + 1, right = nums.size() - 1; // 左右指针
while(left < right && target <= 0)
{
if (nums[left] + nums[right] < -target) left++;
else if (nums[left] + nums[right] > -target) right--;
else
{
ret.push_back({ target, nums[left], nums[right] }); // 更新结果
left++, right--;
// 去重
while(left < right && nums[left] == nums[left - 1]) left++;
while(left < right && nums[right] == nums[right + 1]) right--;
}
}
i++;
// 去重target
while(i < nums.size() - 2 && nums[i] == nums[i - 1]) i++;
}
return ret;
}
};【18.四数之和】
1、题目描述:
2、实现核心即思路:
++a + b + c + d = target++
求满足要求的四个数,我们可以先依次固定一个数作为 a,那么就变成找三个的和等于
target - a,不就转化为对应三数之和的问题了。
解题步骤:
(1)排序(升序);
(2)在数组中从左往右依次固定一个数作为a,转化为三数之和问题(target - a),然后在数组剩下元素中找满足的三个数。
(3)稍微修改上面的三数之和的代码,此时目标值为 target - a,再有两个参数nums 和pos(用来确定数组还剩多少元素)。
代码实现:
cpp
class Solution {
public:
// 找满足三数之和的数
vector<vector<int>> threeSum(vector<int>& nums, int pos, int target_val)
{
vector<vector<int>> ret; // 存储结果
// 从左往右依次固定元素为target
int n = nums.size() - 2;
for(int i = pos + 1; i < n;)
{
long target = (long)nums[i] - (long)target_val; // 目标值
int left = i + 1, right = nums.size() - 1; // 左右指针
while(left < right)
{
if (nums[left] + nums[right] < -target) left++;
else if (nums[left] + nums[right] > -target) right--;
else
{
ret.push_back({ nums[i], nums[left], nums[right] }); // 更新结果
left++, right--;
// 去重
while(left < right && nums[left] == nums[left - 1]) left++;
while(left < right && nums[right] == nums[right + 1]) right--;
}
}
i++;
// 去重target
while(i < nums.size() - 2 && nums[i] == nums[i - 1]) i++;
}
return ret;
}
vector<vector<int>> fourSum(vector<int>& nums, int target)
{
sort(nums.begin(), nums.end()); // 排序
vector<vector<int>> result; // 结果
// 固定一个数作为目标元素之一
int n = nums.size() - 3;
for(int i = 0; i < n;)
{
auto ret = threeSum(nums, i, target - nums[i]);
if(!ret.empty())
{
// 重新完善结果
for(auto e : ret)
{
e.push_back(nums[i]);
result.push_back(e);
}
}
i++;
// 去重 i
while(i < nums.size() - 3 && nums[i] == nums[i - 1]) i++;
}
return result;
}
};