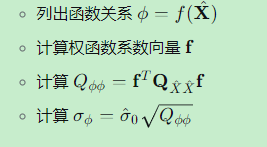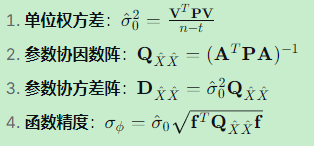误差理论与测量平差基础笔记十

间接平差的精度评定详解

一、精度评定的目的与意义

精度评定是间接平差的必要组成部分，它回答了平差后最核心的两个问题：

观测数据的质量如何？ → 通过单位权中误差评估
参数估计的可信度有多高？ → 通过参数的方差-协方差阵评估

在AGNSS中，精度评定决定了定位结果能否用于导航、测绘等高精度应用。

二、单位权中误差评定

2.1 单位权方差估值公式

2.2 单位权中误差

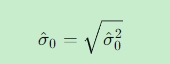
2.3 物理意义

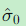是权为1的观测值的中误差估计值
反映了观测系列的整体质量
是所有后续精度评定的基准缩放因子

2.4 统计性质

在观测误差服从正态分布且定权正确的假设下：

2.5 AGNSS中的实际意义

在GNSS定位中：

若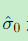远大于预期值（如1m），可能表明：
- 观测条件差（多路径、电离层扰动）
- 有未发现的粗差或周跳
- 数学模型不完善
若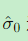远小于预期值，可能表明：
- 观测质量异常好
- 自由度计算错误
- 权阵设定不当

三、参数估值的精度评定

3.1 参数估值的协因数阵

这是精度评定的核心结果：

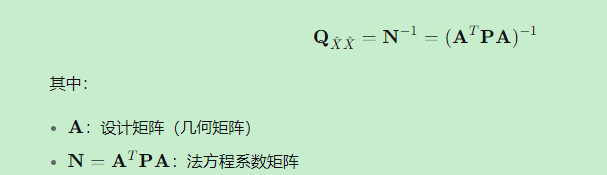
3.2 协因数阵的构成

3.3 参数估值的方差-协方差阵

3.4 参数估值的中误差

第 i个参数的中误差为：

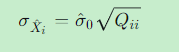
3.5 参数间的相关系数

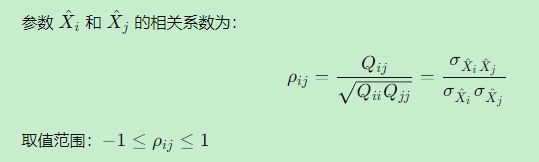
3.6 在GNSS定位中的应用

四、观测值平差值的精度评定

4.1 观测值平差值的协因数阵

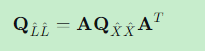
4.2 方差-协方差阵

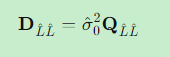
4.3 第 ii 个平差值的中误差

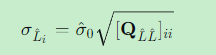
4.4 与改正数中误差的关系

可以证明：

即：平差值方差 + 改正数方差 = 观测值方差

五、参数函数的精度评定

5.1 一般函数形式

在实际应用中，我们关心的往往是参数的函数：

示例：

从直角坐标 (X, Y, Z)计算大地坐标 (B, L, H)
计算两点间的距离
计算方位角或高度角

5.2 线性化与权函数式

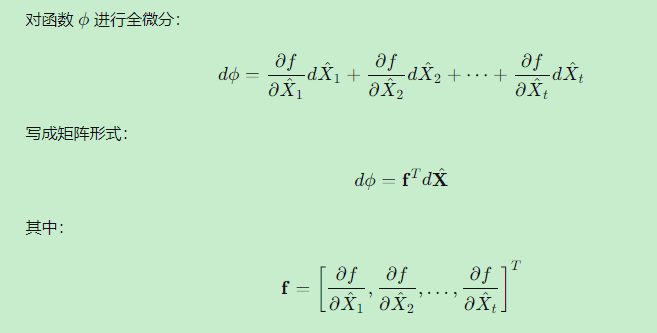
称为权函数系数向量。

5.3 函数 ϕ 的协因数

应用协因数传播律：

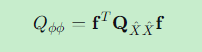
5.4 函数 ϕ 的方差和中误差

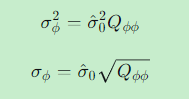
5.5 多个参数函数的协因数阵

六、AGNSS中的关键应用：从XYZ到ENU的精度转换

6.1 坐标转换函数

在GNSS中，我们通常需要将地心地固坐标系（ECEF）下的精度转换到当地站心坐标系（ENU）。

转换关系：

6.2 精度传播计算

6.3 提取常用精度指标

6.4 误差椭圆（水平精度分布）

七、精度评定的完整流程

7.1 计算步骤

计算单位权方差：
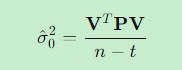
计算参数协因数阵：
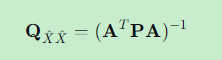
计算参数协方差阵：
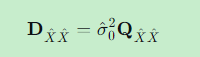
提取参数精度：
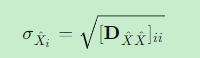
计算平差值精度（如需）：
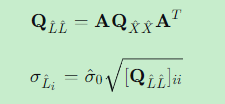
计算参数函数的精度：

7.2 AGNSS中的实际计算

复制代码

def indirect_adjustment_precision(A, P, V, X_hat):
    """
    间接平差精度评定函数
    """
    n, t = A.shape
    
    # 1. 单位权方差
    sigma0_sq = (V.T @ P @ V) / (n - t)
    sigma0 = np.sqrt(sigma0_sq)
    
    # 2. 参数协因数阵和协方差阵
    N = A.T @ P @ A
    Q_XX = np.linalg.inv(N)
    D_XX = sigma0_sq * Q_XX
    
    # 3. 参数中误差
    sigma_X = np.sqrt(np.diag(D_XX))
    
    # 4. 坐标转换到ENU（示例）
    # 假设XYZ是前3个参数
    Q_XYZ = Q_XX[:3, :3]
    
    # 旋转矩阵（假设已知测站经纬度）
    lat = np.radians(30)  # 纬度30度
    lon = np.radians(120) # 经度120度
    
    R = np.array([
        [-np.sin(lon), np.cos(lon), 0],
        [-np.sin(lat)*np.cos(lon), -np.sin(lat)*np.sin(lon), np.cos(lat)],
        [np.cos(lat)*np.cos(lon), np.cos(lat)*np.sin(lon), np.sin(lat)]
    ])
    
    # ENU协因数阵和协方差阵
    Q_ENU = R @ Q_XYZ @ R.T
    D_ENU = sigma0_sq * Q_ENU
    
    # 5. 提取水平精度指标
    sigma_E = np.sqrt(D_ENU[0, 0])
    sigma_N = np.sqrt(D_ENU[1, 1])
    sigma_U = np.sqrt(D_ENU[2, 2])
    
    # 水平精度指标
    DRMS = np.sqrt(sigma_E**2 + sigma_N**2)
    CEP = 0.59 * (sigma_E + sigma_N)  # 近似公式
    
    # 6. 误差椭圆参数
    D_EN = D_ENU[:2, :2]
    eigenvalues, eigenvectors = np.linalg.eig(D_EN)
    idx = eigenvalues.argsort()[::-1]
    lambda1, lambda2 = eigenvalues[idx]
    
    # k=1对应约39%置信椭圆，k=2.15对应95%置信椭圆
    k = 2.15  # 95%置信水平
    a = k * np.sqrt(lambda1)  # 长半轴
    b = k * np.sqrt(lambda2)  # 短半轴
    
    # 椭圆方位角（从北顺时针）
    theta_rad = 0.5 * np.arctan2(2*D_ENU[0,1], D_ENU[0,0]-D_ENU[1,1])
    theta_deg = np.degrees(theta_rad)
    
    return {
        'sigma0': sigma0,
        'sigma_X': sigma_X,
        'D_XX': D_XX,
        'sigma_E': sigma_E,
        'sigma_N': sigma_N,
        'sigma_U': sigma_U,
        'DRMS': DRMS,
        'CEP': CEP,
        'error_ellipse': {
            'major_axis': a,
            'minor_axis': b,
            'orientation': theta_deg
        }
    }