【LeetCode刷题】二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的中序遍历 。

示例 1：

复制代码

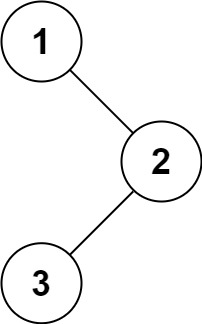
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

复制代码

输入：root = []
输出：[]

示例 3：

复制代码

输入：root = [1]
输出：[1]

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100

递归解法

利用递归的 "左→根→右" 顺序遍历，是中序遍历的直观实现。

Python代码

python 复制代码

from typing import Optional, List


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        result = []

        # 递归辅助函数：实现中序遍历「左→根→右」的核心逻辑
        def traverse(node: Optional[TreeNode]):
            if node:  # 节点非空时才遍历，递归终止条件：node is None
                traverse(node.left)  # 第一步：遍历左子树
                result.append(node.val)  # 第二步：访问当前根节点
                traverse(node.right)  # 第三步：遍历右子树

        traverse(root)  # 从根节点开始递归遍历
        return result


if __name__ == "__main__":
    # 实例化解题类
    sol = Solution()

    # 示例1：构建树 [1,null,2,3] → 输出 [1,3,2]
    root1 = TreeNode(1)
    root1.right = TreeNode(2)
    root1.right.left = TreeNode(3)
    print("示例1输出：", sol.inorderTraversal(root1))
    print("预期结果：", [1, 3, 2])
    print("-" * 30)

    # 示例2：构建空树 [] → 输出 []
    root2 = None
    print("示例2输出：", sol.inorderTraversal(root2))
    print("预期结果：", [])
    print("-" * 30)

    # 示例3：构建树 [1] → 输出 [1]
    root3 = TreeNode(1)
    print("示例3输出：", sol.inorderTraversal(root3))
    print("预期结果：", [1])

LeetCode提交代码

python 复制代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        result = []
        # 递归辅助函数：实现"左→根→右"的遍历逻辑
        def traverse(node: Optional[TreeNode]):
            if node:
                traverse(node.left)  # 先遍历左子树
                result.append(node.val)  # 再访问当前根节点
                traverse(node.right)  # 最后遍历右子树
        traverse(root)
        return result

程序运行截图展示

总结

本文介绍了二叉树中序遍历的递归实现方法。中序遍历按照"左子树→根节点→右子树"的顺序访问节点。通过Python代码演示了递归解法，定义了一个辅助函数traverse来实现这一逻辑：先递归遍历左子树，然后访问当前节点值，最后递归遍历右子树。提供了三个测试用例验证正确性：包含单节点树、空树和典型二叉树的情况。时间复杂度为O(n)，空间复杂度为O(n)（递归栈空间）。该方法直观体现了中序遍历的定义，是解决此类问题的经典递归范式。