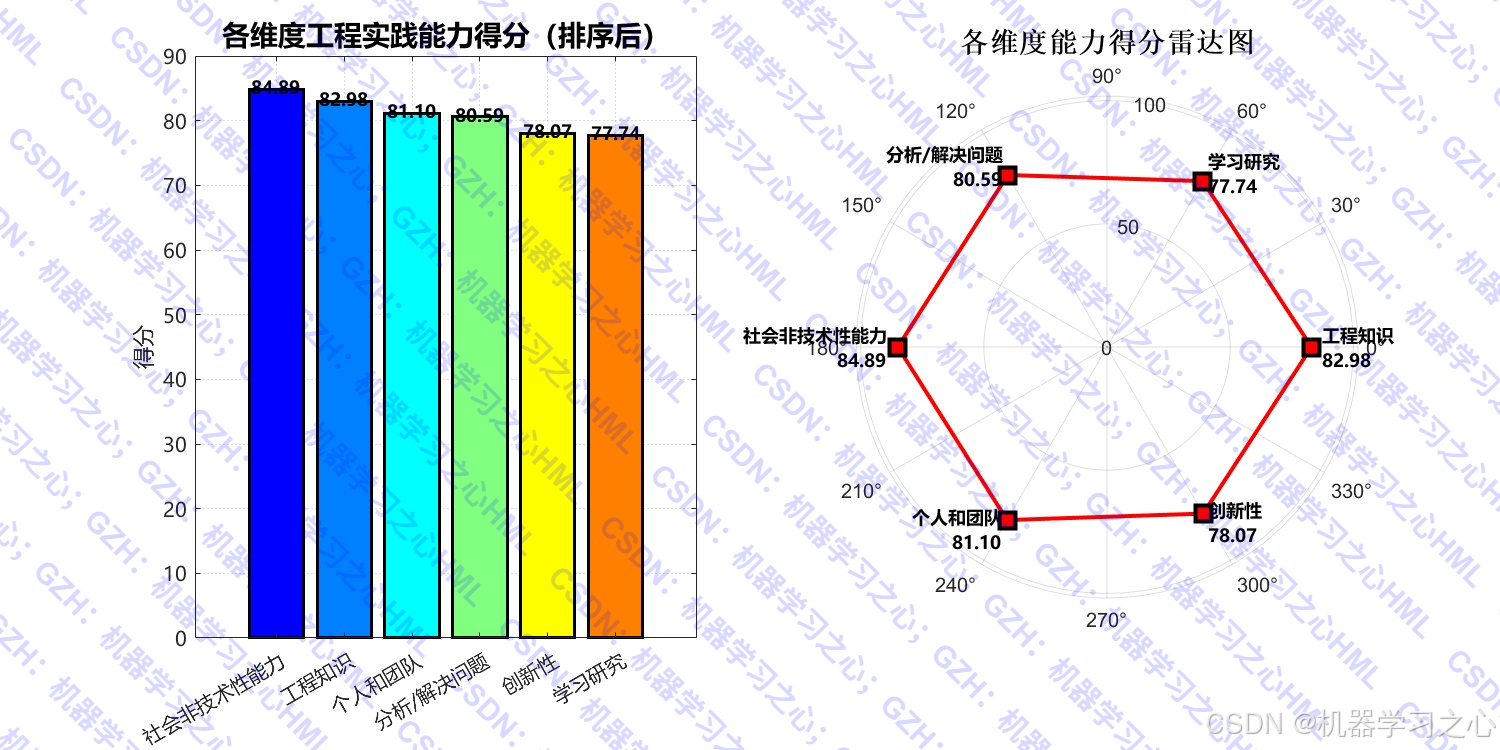
这段MATLAB代码实现了一个基于AHP(层次分析法)-模糊综合评价法的工程实践能力评价系统,适用于对工程类学生或从业者的综合能力进行量化评估与可视化分析。
一、研究背景
- 工程教育认证需求:国内外工程教育认证(如ABET、中国工程教育专业认证)强调对学生"工程实践能力"的量化评价。
- 多维度评价需求:工程实践能力涉及知识、技能、团队协作、创新等多个维度,需综合使用定性与定量方法。
- AHP与模糊数学结合:AHP适用于权重确定,模糊综合评价适用于处理主观评价的不确定性,二者结合可提升评价的科学性与合理性。
二、主要功能
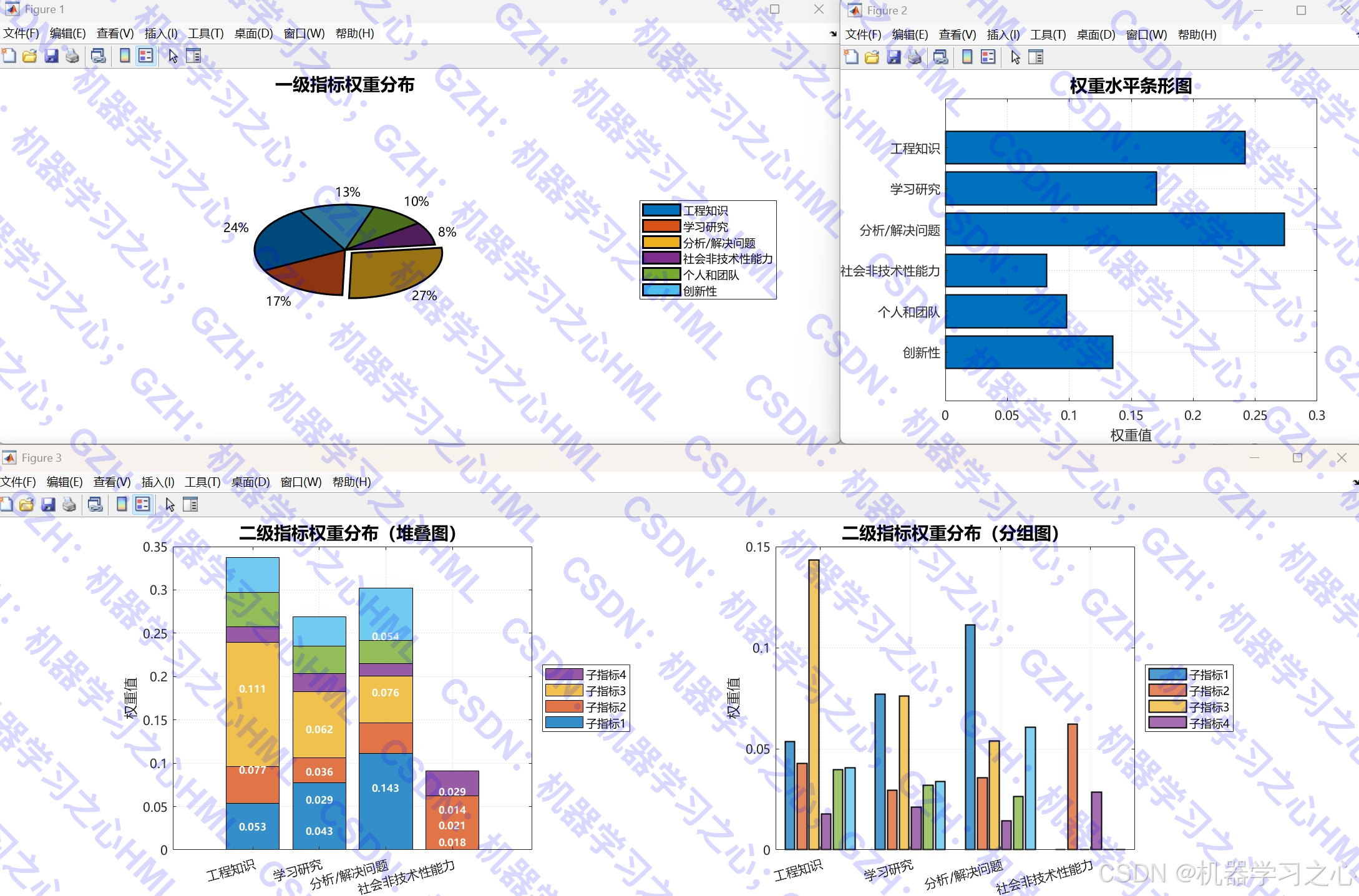
- AHP权重计算:构建判断矩阵,计算一级与二级指标权重,并进行一致性检验。
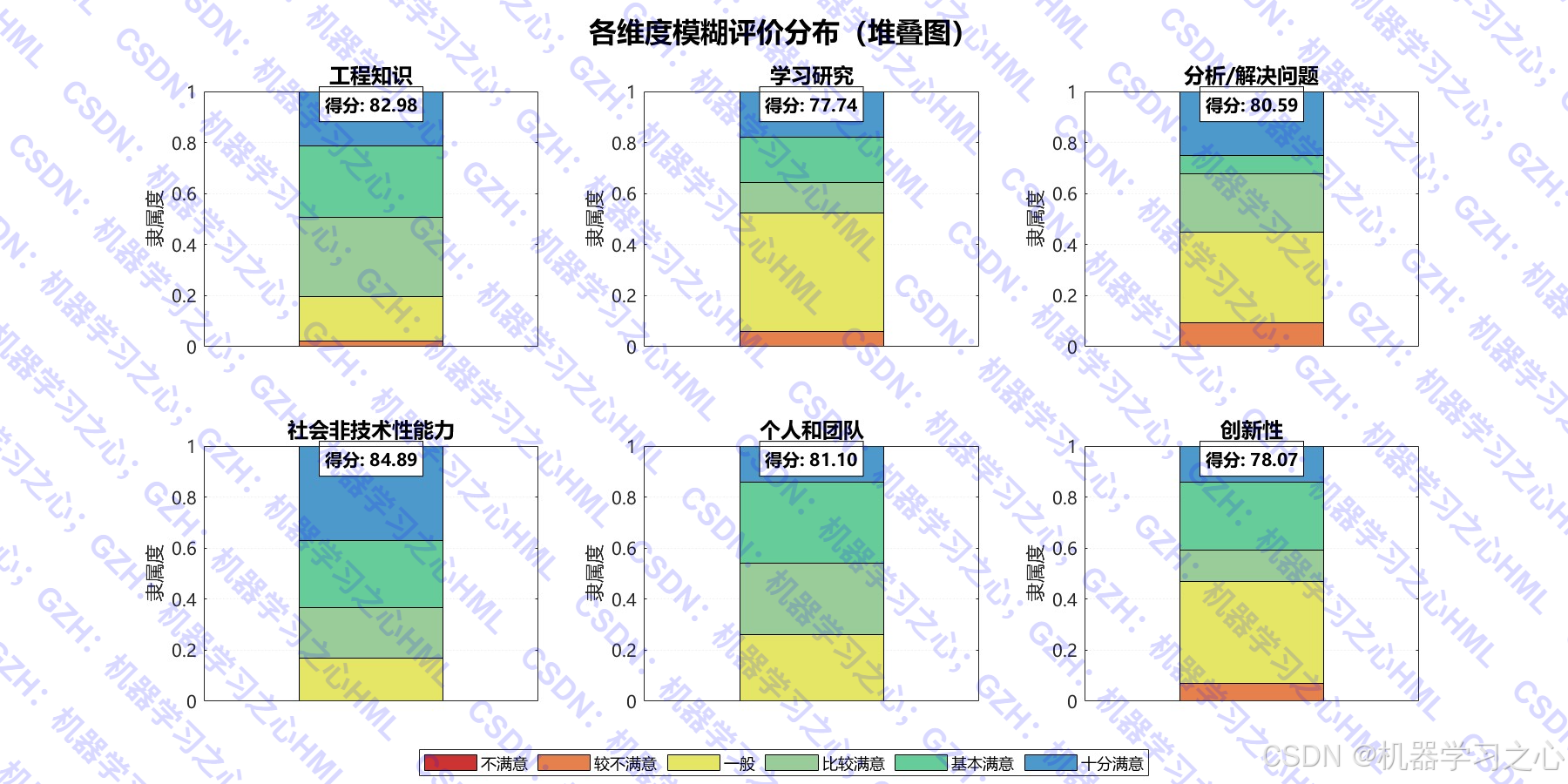
- 模糊综合评价:基于模糊隶属度矩阵,计算各维度及总体评价得分。
- 多维度可视化 :
- 权重分布图(饼图、柱状图)
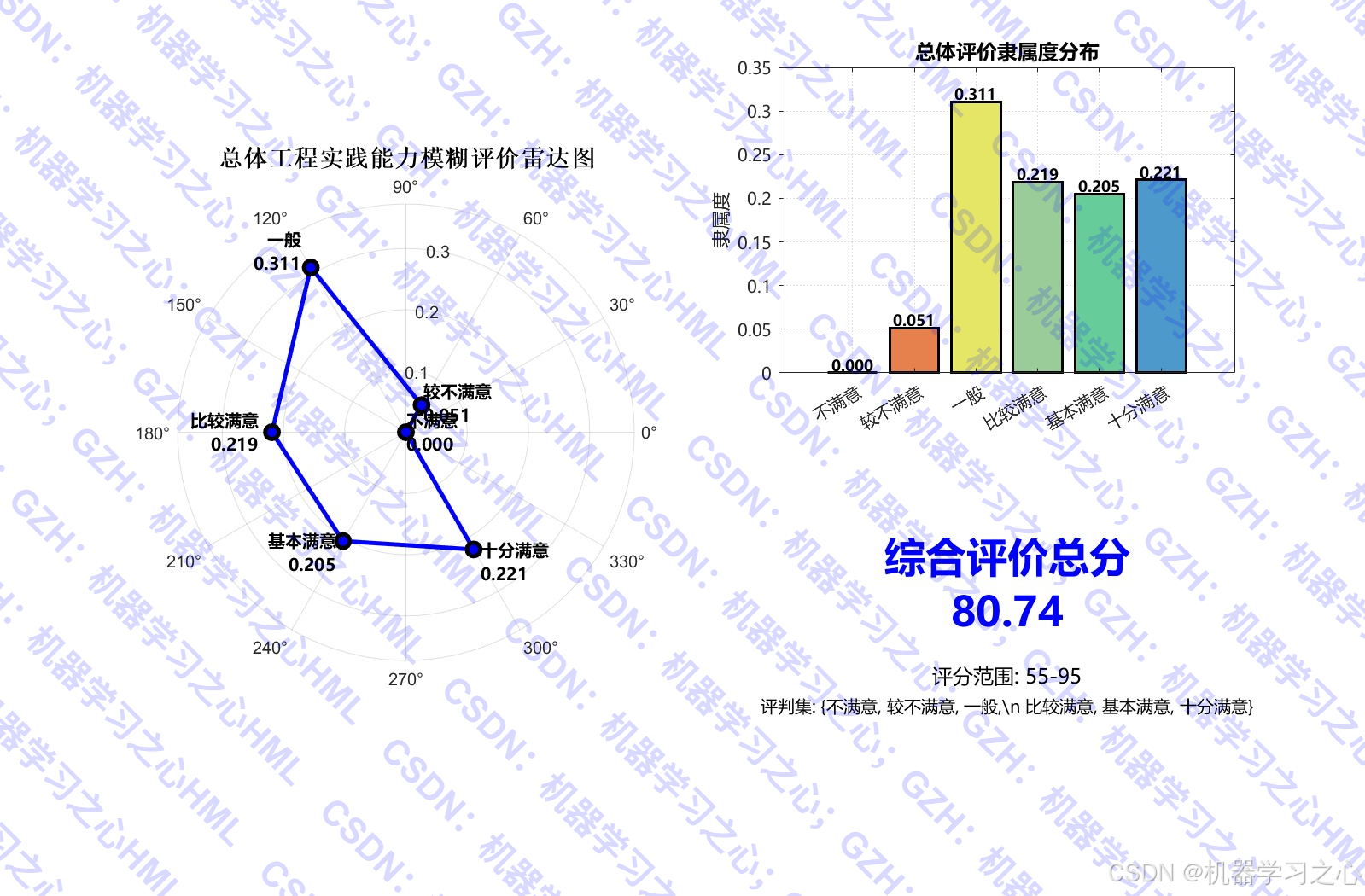
- 评价结果雷达图、堆叠图、热力图
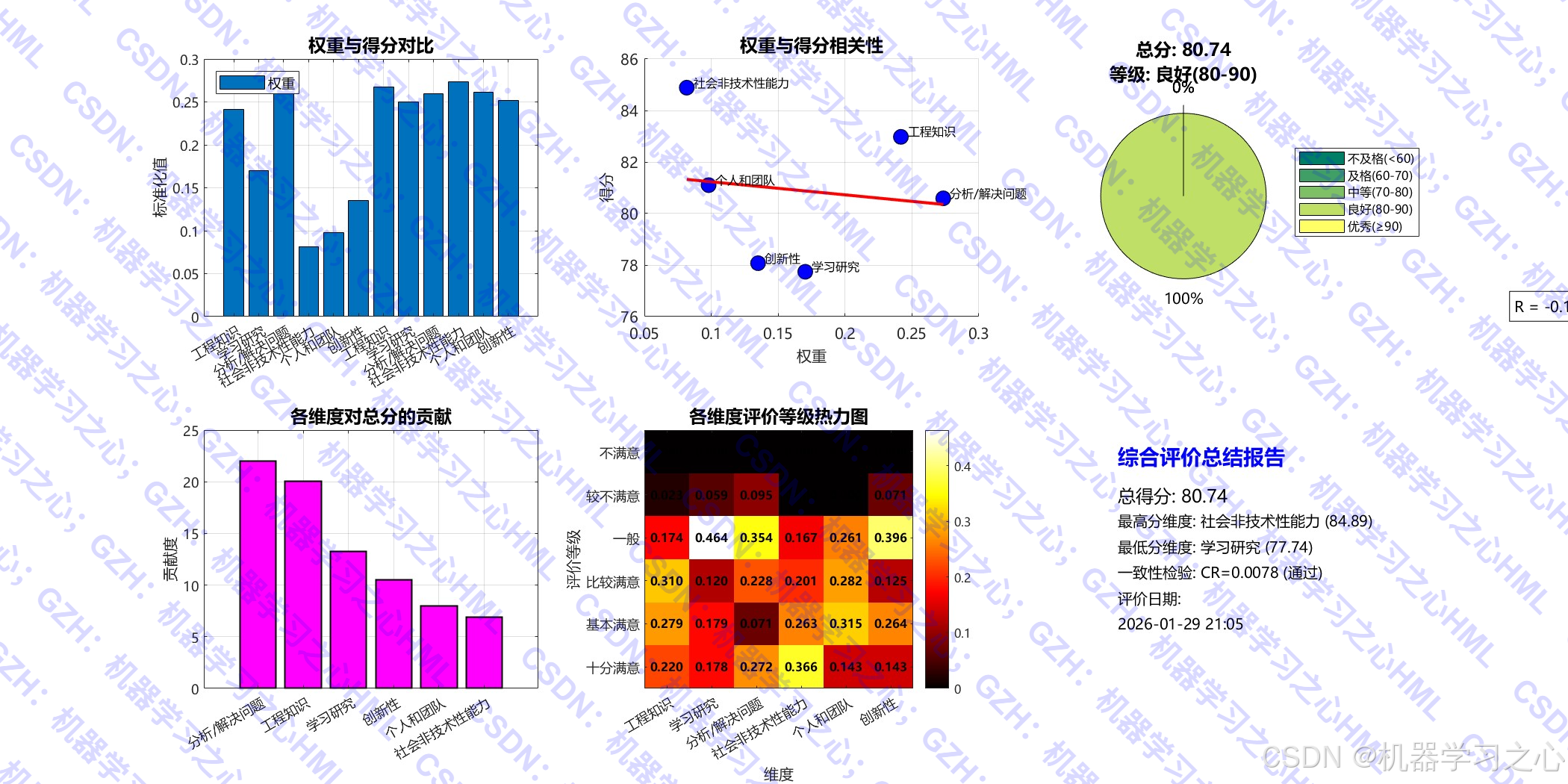
- 综合报告图(包含相关性分析、贡献度分析等)
三、算法步骤
-
AHP部分:
- 输入判断矩阵 A A A
- 计算最大特征值 λ max \lambda_{\text{max}} λmax和特征向量
- 归一化得权重向量 W
- 计算 C I CI CI和 C R CR CR,进行一致性检验
-
模糊综合评价部分:
- 输入各维度模糊评价矩阵 R R R
- 结合权重向量 A 1 A1 A1,计算总体评价向量 B total B_{\text{total}} Btotal
- 基于评判集得分向量 V scores V_{\text{scores}} Vscores 计算总分
-
可视化部分:
- 绘制权重与评价结果的多类图表
- 生成综合报告图
四、技术路线
- 建模方法:AHP + 模糊综合评价
- 编程语言:MATLAB
- 可视化工具:MATLAB图形系统(pie, bar, polarplot, imagesc等)
- 数据处理:矩阵运算、特征值分解、归一化处理
五、公式原理
-
AHP权重计算 :
A W = λ max W AW = \lambda_{\text{max}}W AW=λmaxW
C I = λ max − n n − 1 , C R = C I R I CI = \frac{\lambda_{\text{max}} - n}{n - 1}, \quad CR = \frac{CI}{RI} CI=n−1λmax−n,CR=RICI -
模糊综合评价 :
B = A ∘ R B = A \circ R B=A∘R
总分 = B × V T \text{总分} = B \times V^T 总分=B×VT
六、参数设定
- 一级指标:6个(工程知识、学习研究、分析/解决问题、社会非技术性能力、个人和团队、创新性)
- 二级指标:6组共21个子指标(部分补零对齐)
- 评判集:6个等级(不满意 ~ 十分满意),对应分数为 ( [55, 60, 70, 80, 85, 95] )
- 一致性检验RI值:1.26(针对6阶矩阵)
七、运行环境
- 平台:MATLAB R2018a及以上版本(推荐)
八、应用场景
- 工程教育评价:高校工程专业学生实践能力评估
- 企业人才评估:工程师能力考核与晋升评价
- 项目团队评估:多维度评估团队综合能力
- 教学改进反馈:通过评价结果指导课程与实训设计