02_神经网络如何自动求导?反向传播的数学魔法
本章目标 :揭开深度学习框架最神秘的面纱 ------ 自动微分 (Autograd) 。我们将从最基础的链式法则 (Chain Rule) 出发,手写一个微型计算图引擎。
📖 目录 (Table of Contents)
- 从手算到图算:思维的转变
- 链式法则:梯度的"接力赛"
- [计算图 (Computational Graph):把运算变成节点](#计算图 (Computational Graph):把运算变成节点)
- [实战:手撕 Autograd 引擎 (不调包)](#实战:手撕 Autograd 引擎 (不调包))
- [PyTorch 的魔法:.backward() 到底干了什么?](#PyTorch 的魔法:.backward() 到底干了什么?)
1. 从手算到图算:思维的转变
在第1章,我们手算了 L o s s = ( x ⋅ w − y ) 2 Loss = (x \cdot w - y)^2 Loss=(x⋅w−y)2 的导数。
如果是 AlexNet(8层),也许还能手算。但如果是 ResNet-152(152层),手算全导数的公式写出来可能比万里长城还长。
我们需要一种通用的、模块化的求导方法。
这就好比:不要试图一步算出整个公司的利润,而是让每个部门算出自己的利润,最后汇总。
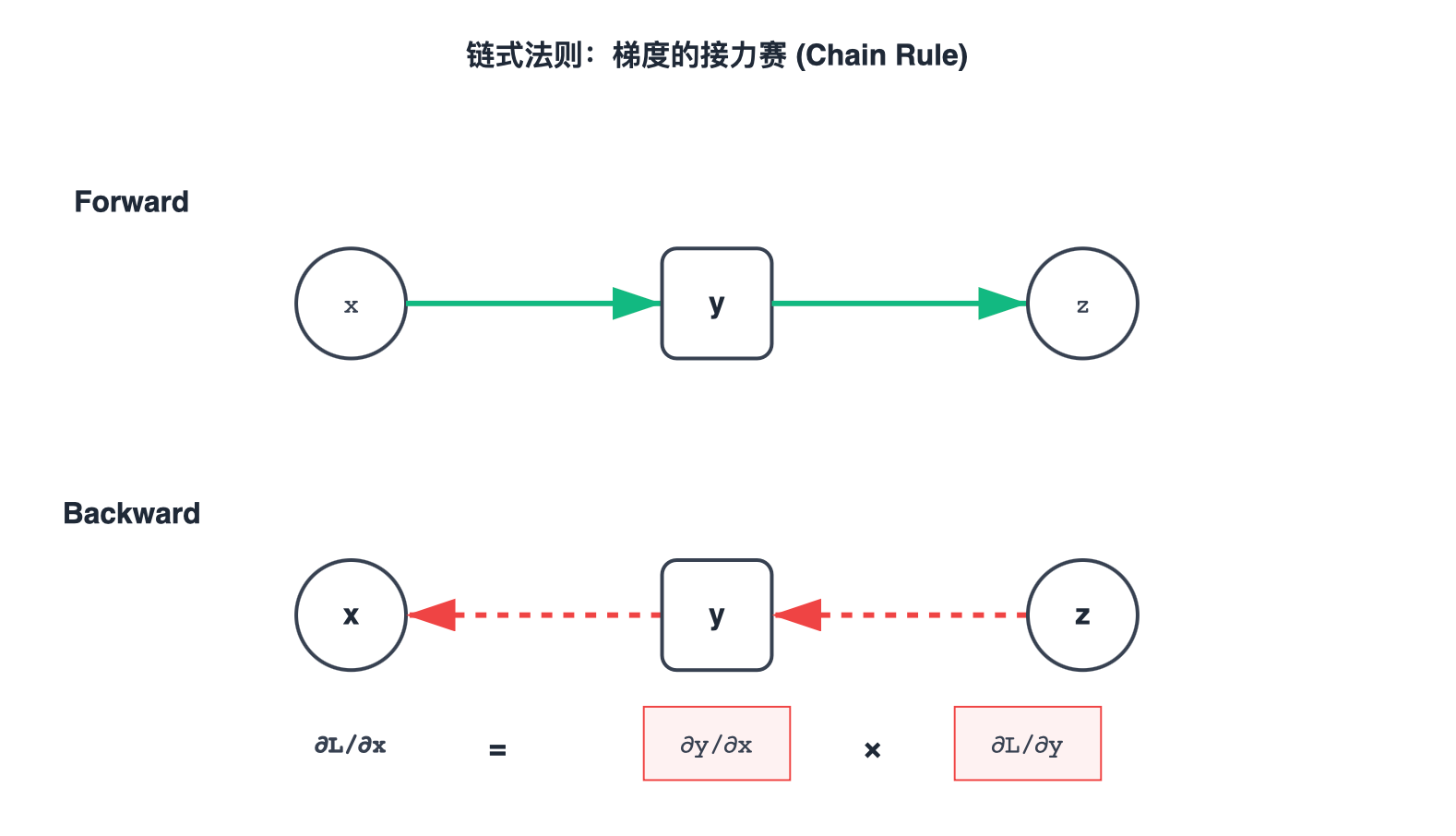
2. 链式法则:梯度的"接力赛"
由复合函数 y = f ( u ) , u = g ( x ) y = f(u), u = g(x) y=f(u),u=g(x),即 y = f ( g ( x ) ) y = f(g(x)) y=f(g(x))。
链式法则告诉我们:
∂ y ∂ x = ∂ y ∂ u ⋅ ∂ u ∂ x \frac{\partial y}{\partial x} = \frac{\partial y}{\partial u} \cdot \frac{\partial u}{\partial x} ∂x∂y=∂u∂y⋅∂x∂u
这听起来很简单,但在神经网络中,它意味着:
如果你想知道这一层对最终 Loss 的影响,你只需要知道:
- 上游梯度 (Upstream Gradient):Loss 对下一层的影响。
- 本地梯度 (Local Gradient):你这层对下一层的导数。
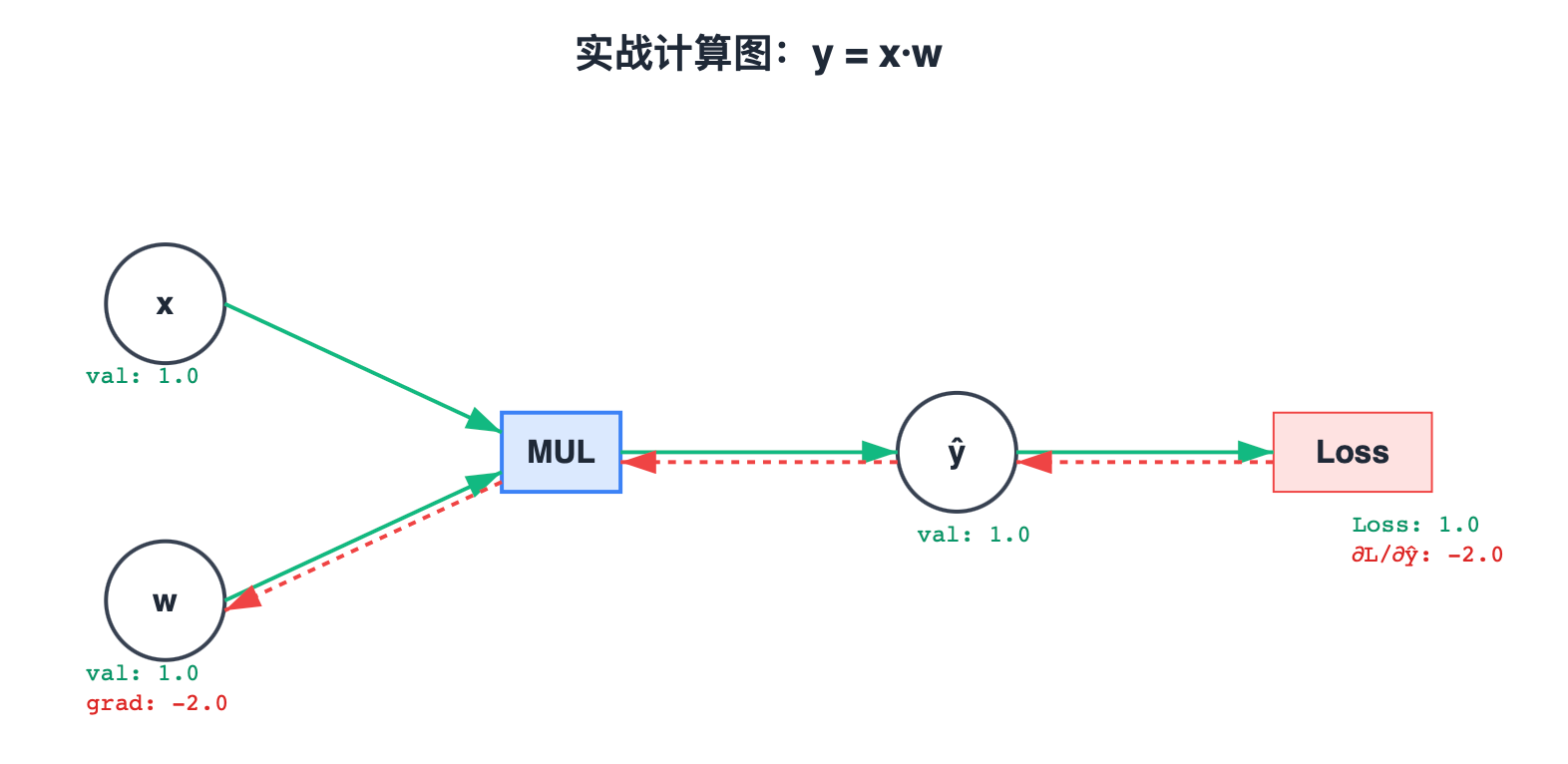
3. 计算图 (Computational Graph):把运算变成节点
为了实现自动化,我们将数学公式拆解为图 (Graph) 。
每一个节点(加、减、乘、平方)都是一个守门人。它只需要管好自己的"Local Gradient"。
让我们画出 L o s s = ( x ⋅ w − T a r g e t ) 2 Loss = (x \cdot w - Target)^2 Loss=(x⋅w−Target)2 的计算图:
4. 实战:手撕 Autograd 引擎 (不调包)
为了彻底理解,我们用 Python Class 模拟这个过程。
python
class Tensor:
def __init__(self, data, requires_grad=False):
self.data = data
self.grad = 0.0
self.requires_grad = requires_grad
self.grad_fn = None
def backward(self, grad=1.0):
self.grad += grad
if self.grad_fn:
self.grad_fn(grad)
def __mul__(self, other):
out = Tensor(self.data * other.data, requires_grad=True)
def backward_fn(upstream_grad):
if self.requires_grad:
self.backward(upstream_grad * other.data)
if other.requires_grad:
other.backward(upstream_grad * self.data)
out.grad_fn = backward_fn
return out
def square(self):
out = Tensor(self.data ** 2, requires_grad=True)
def backward_fn(upstream_grad):
if self.requires_grad:
self.backward(upstream_grad * (2 * self.data))
out.grad_fn = backward_fn
return out
# === 验证 ===
x = Tensor(1.0, requires_grad=False)
w = Tensor(1.0, requires_grad=True)
t = Tensor(2.0, requires_grad=False)
# Forward
y = x * w
diff = y - t
loss = diff.square()
print(f"Loss data: {loss.data}")
# Backward
loss.backward()
print(f"w.grad: {w.grad}")5. PyTorch 的魔法:.backward() 到底干了什么?
当我们调用 loss.backward() 时,PyTorch 做的事情和我们刚才的代码一模一样:
- 找到
loss的grad_fn。 - 计算局部梯度。
- 乘以传入的梯度。
- 递归调用父节点的
grad_fn。 - 直到遇到叶子节点(如
w),把由于累加到w.grad中。