高阶数据结构:并查集
高阶数据结构:并查集
github地址
前言
在很多工程与算法问题中,我们经常会遇到这样一类场景:
需要将一堆元素动态划分成若干个互不相交的集合,并支持:
- 查询某个元素属于哪个集合
- 判断两个元素是否属于同一集合
- 合并两个集合
这类问题如果用普通数组或树来处理,往往复杂且低效。而**并查集(Union-Find Set)**正是为此类问题量身定制的高效数据结构。
一、什么是并查集
在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并 。在此过程中要反复用到查询某一个元素归属于那个集合的运算。
适合于描述这类问题的抽象数据类型称为并查集(union-find set)。
并查集是一种树型结构的数据结构 ,用来维护若干个不相交集合。
它支持三种核心操作:
| 核心操作 | 说明 |
|---|---|
Find |
查找某元素属于哪个集合 |
Union |
合并两个集合 |
IsInSet |
判断两个元素是否在同一集合 |
适合描述"集合合并 + 归属查询"问题的抽象数据类型,称为并查集(
Union-Find Set)。
二、并查集的原理理解
比如:某公司今年校招全国总共招生10人,西安招4人,成都招3人,武汉招3人,10个人来自不同的学校,起先互不相识,每个学生都是一个独立的小团体,现给这些学生进行编号:
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9};
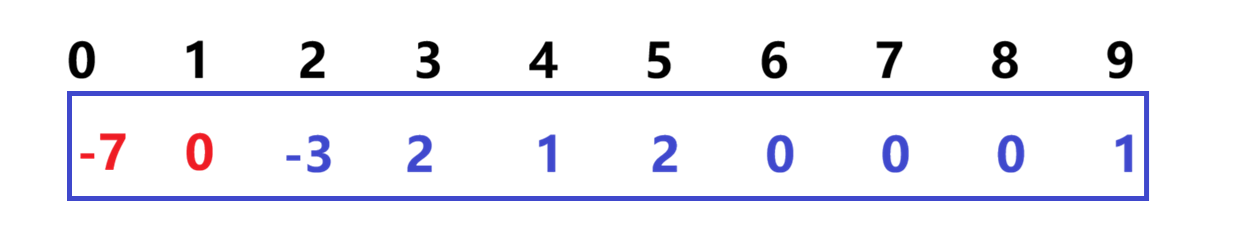
用以下数组用来存储该小集体,数组中的数字代表:该小集体中具有成员的个数。(负号下文解释)
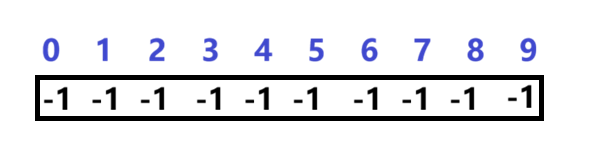
毕业后,学生们要去公司上班,每个地方的学生自发组织成小分队一起上路,于是:
西安学生小分队 s1={0,6,7,8} ,成都学生小分队 s2={1,4,9} ,武汉学生小分队 s3={2,3,5} 就相互认识了,10个人形成了三个小团体。假设由0, 1, 2担任队长,负责大家的出行。
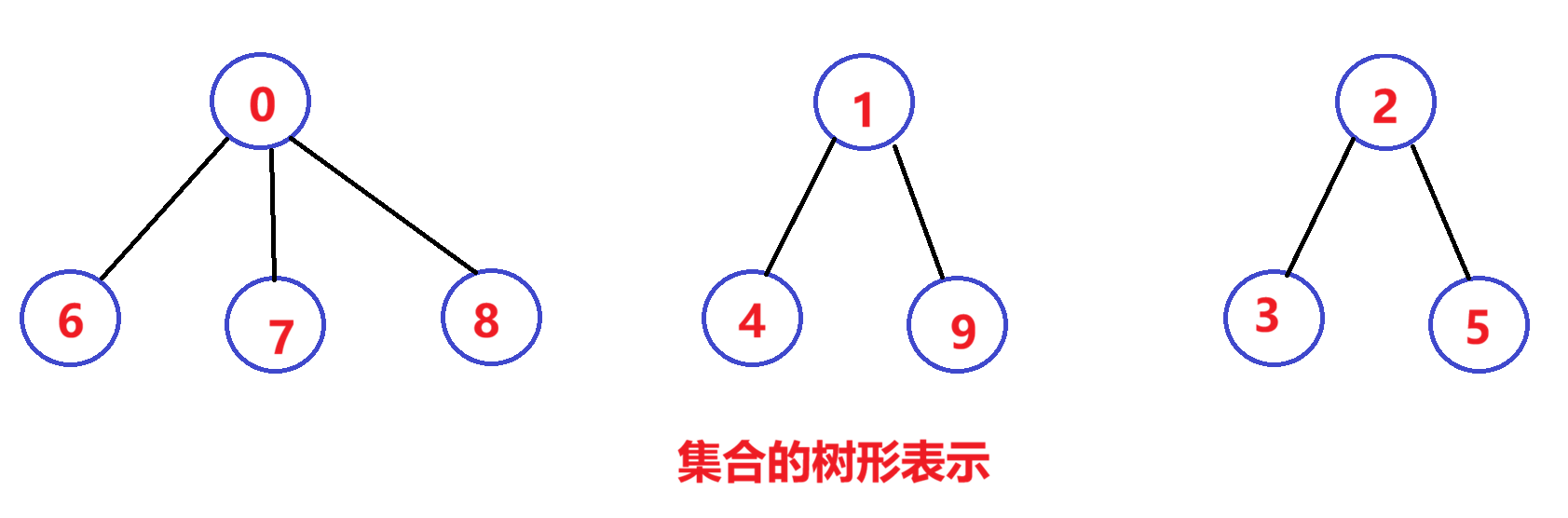
一趟火车之旅后,每个小分队成员就互相熟悉,成为了一个朋友圈。
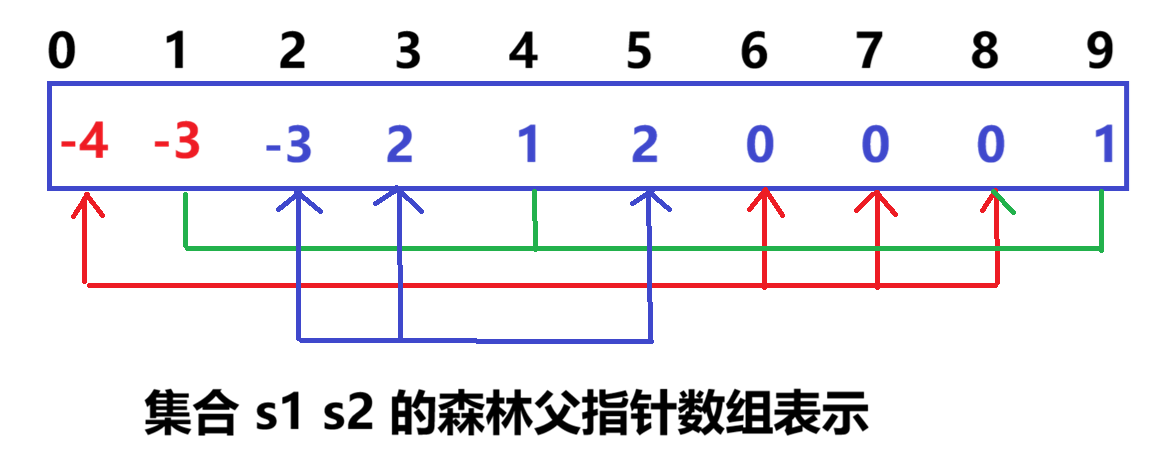
从上图可以看出:编号
6, 7, 8同学属于 0 号小分队,该小分队中有4人(包含队长0);编号为4和9的同学属于1号小分队,该小分队有3人(包含队长1);
编号为3和5的同学属于2号小分队,该小分队有3个人(包含队长1)。
仔细观察数组中内容,可以得出以下结论:
- 数组的下标对应集合中元素的编号
- 数组中如果为负数,负号代表根,数字代表该集合中元素个数
- 数组中如果为非负数,代表该元素双亲在数组中的下标
在公司工作一段时间后,西安小分队中8号同学与成都小分队1号同学奇迹般的走到了一起,两个小圈子的学生相互介绍,最后成为了一个小圈子
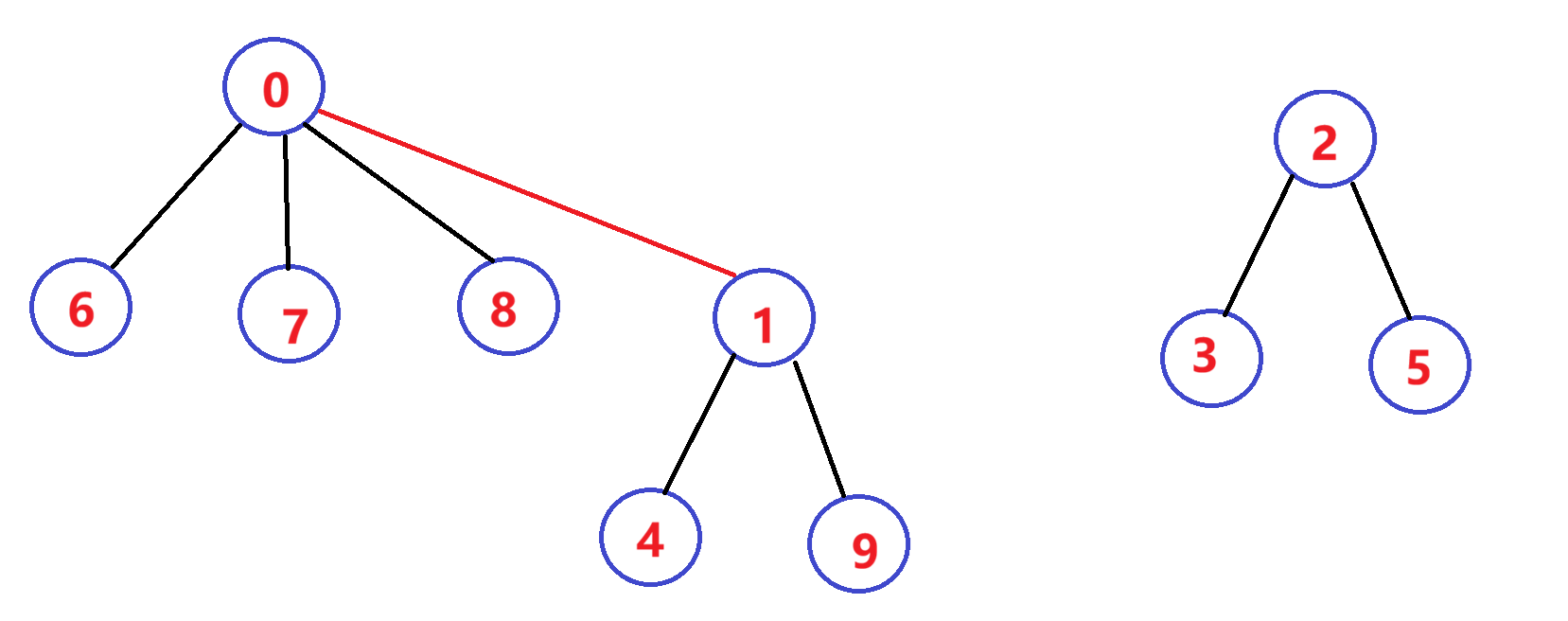
现在0集合有7个人,2集合有3个人,总共两个朋友圈。
通过以上例子可知,并查集一般可以解决以下问题:
-
查找元素属于哪个集合
沿着数组表示树形关系往上一直找到根(即:树中中元素为负数的位置)
-
查看两个元素是否属于同一个集合
沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在
-
将两个集合归并成一个集合
-
将两个集合中的元素合并
-
将一个集合名称改成另一个集合的名称
-
-
集合的个数
遍历数组,数组中元素为负数的个数即为集合的个数。
数组含义:
- 下标 = 元素编号
- 负数 = 根节点,绝对值 = 当前集合大小
- 非负数 = 该元素的父节点下标
三、并查集的C++实现
类结构设计
cpp
// 每个集合都是一棵树
// 并查集 逻辑结构是一个森林
class UnionFindSet
{
public:
UnionFindSet(size_t n);
int FindRoot(int index);
void Union(int index1, int index2);
bool IsInSet(int index1, int index2);
size_t SetCount() const;
private:
vector<int> _ufs;
};用vector来抽象存储并查集:
-
下标 = 元素编号
-
负数 = 根节点,绝对值 = 当前集合大小
-
非负数 = 该元素的父节点下标
构造函数
cpp
// 用 n 个数字构造并查集, 0 - n-1 为下标, vector 中存 正数或负数
// 存负数: 代表当前 下标所代表的元素 为根
// 存 >=0 的数: 该数为 当前元素的父节点的 下标
UnionFindSet(size_t n)
:_ufs(n, -1)
{}思路与解释:
- 对 n 个元素,创建 n 个集合,每个元素初始都是一个根,即每个元素初始都是一个单独的集合
vector中存储的值为-1表示:- 该元素是根
- 集合大小为 1
查找元素的根结点
非路径压缩版本
cpp
int FindRoot(int index) // 找当前元素的根结点的下标
{
int parent = index; // 刚开始,每个元素都是一个独立的的根
// 找根小于0的位置
while (_ufs[parent] >= 0)
{
parent = _ufs[parent];
}
return parent;
}查找根节点思路与解释:
- 从当前节点向父节点不断回溯,
_ufs[parent] >= 0时,说明当前记录的是父节点的下标 - 直到遇到
_ufs[parent] < 0,说明这是根结点 - 返回根下标
路径压缩版本
cpp
int FindRoot(int index) // 找当前元素的根结点的下标
{
// 1. 找根 的下标
int root = index;
while (_ufs[root] >= 0)
{
root = _ufs[root];
}
// 2. 压缩路径
int cur = index;
while (_ufs[cur] >= 0)
{
int parent = _ufs[cur]; // 保存父亲
_ufs[cur] = root; // 将父亲改成跟
cur = parent; // 更新 cur
}
return root;
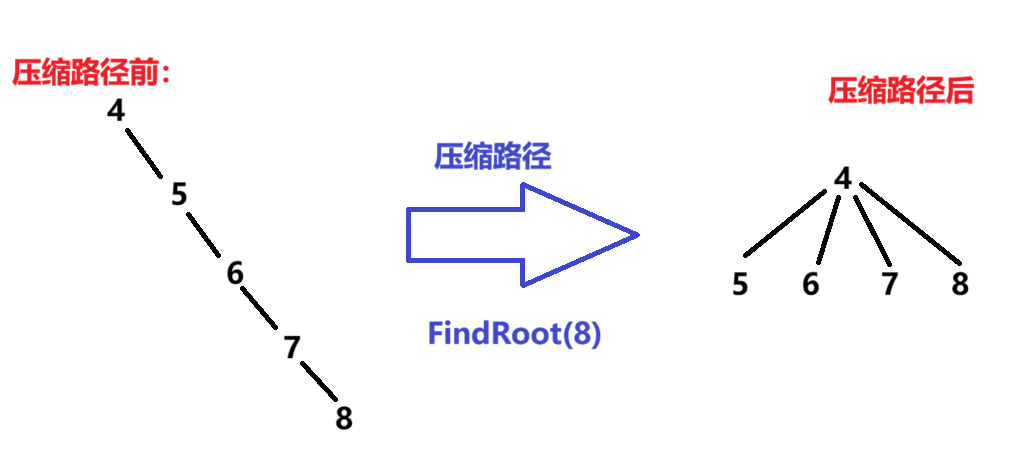
}路径压缩的思路阐述:
- 第一步和非路径压缩版本一致,找出当前并查集中的根节点下标
- 再从当前下标位置开始找,对应位置存储的值 >= 0时,将其父节点更新为根节点
将两元素合并到同一集合
cpp
void Union(int index1, int index2) // 将两个成员合并成一个集合
{
int root1 = FindRoot(index1);
int root2 = FindRoot(index2);
if (root1 == root2) // 两元素的根相同,即本身就在同一个集合,则不合并
return;
// 数据量小的集合 合并到 数据量大的集合 _ufs[root] 越小(越负),集合越大
// 作为子树合并的集合,层数会增加一层,因此要将 大集合 合并到 小集合
if (_ufs[root1] > _ufs[root2])
std::swap(root1, root2);
// 合并的逻辑
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}思路与解释:
- 找到两个集合的根
- 若相同 → 已在同一集合,无需合并。根不相同时再继续合并
- 将小集合合并到大集合
- **合并根的逻辑:**小集合合并到大集合,防止大集合层数过高
- 更新大集合的元素个数 :
_ufs[root1] += _ufs[root2]; - 小集合的根指向大集合 :
_ufs[root2] = root1;
- 更新大集合的元素个数 :
判断两元素是否在同一集合
cpp
bool IsInSet(int index1, int index2) // 判断两个元素是否在同一个集合
{
int root1 = FindRoot(index1);
int root2 = FindRoot(index2);
return root1 == root2; // 两个元素有相同的根,则在同一个集合
}思路与解释:
- 两个元素有相同的根,则在同一个集合
计算集合个数
cpp
// 数组中有几个值是负数,就有几个集合
size_t SetCount() const // 返回当前并查集中 集合的个数
{
size_t count = 0;
for (size_t i = 0; i < _ufs.size(); ++i)
{
if (_ufs[i] < 0)
++count;
}
return count;
}思路与解释:
- 数组中负数的个数 = 当前集合个数
建立下标与任意类型映射
cpp
// 建立了 下标和人名索引的并查集
template<class T>
class UnionFindSet
{
public:
// 给了一个包含姓名的数组,把他存入一个 vector 中即可,可以通过编号找人
UnionFindSet(const T* arr, size_t size)
{
for (size_t i = 0; i < size; ++i)
{
_arr.push_back(arr[i]);
_indexMap[arr[i]] = i;
}
}
private:
vector<T> _arr; // 用编号找姓名
map<T, int> _indexMap; // 用姓名找编号
};作用
- 支持字符串、人名等非整数类型
- 通过 map 建立 对象 → 编号 的映射
五、完整代码实现
cpp
#pragma once
#include <iostream>
#include <vector>
#include <map>
#include <string>
using namespace std;
//// 建立了 下标和人名索引的并查集
//template<class T>
//class UnionFindSet
//{
//public:
// // 给了一个包含人名的数组,把他存入一个 vector 中即可,可以通过编号找人
// UnionFindSet(const T* arr, size_t size)
// {
// for (size_t i = 0; i < size; ++i)
// {
// _arr.push_back(arr[i]);
// _indexMap[arr[i]] = i;
// }
// }
//private:
// vector<T> _arr; // 用编号找人
// map<T, int> _indexMap; // 用人找编号
//};
// 这里没有人名,假设给出的都是数字
// 并查集 逻辑结构是一个森林
class UnionFindSet
{
public:
// 用 n 个数字构造并查集, 0-n 为下标, vector 中存数字
// 存负数: 代表当前 下标所代表的元素 为根
// 存 >=0 的数: 该数为 当前元素的父节点的 下标
UnionFindSet(size_t n)
:_ufs(n, -1)
{}
// 提供如下成员函数
void Union(int index1, int index2) // 将两个成员合并成一个集合
{
int root1 = FindRoot(index1);
int root2 = FindRoot(index2);
if (root1 == root2) // 两元素的根相同,即本身就在同一个集合,则不合并
return;
// 数据量小的集合 合并到 数据量大的集合 _ufs[root] 越小(越负),集合越大
// 作为子树合并的集合,层数会增加一层,因此要将 大集合 合并到 小集合
if (_ufs[root1] > _ufs[root2])
std::swap(root1, root2);
// 合并的逻辑
_ufs[root1] += _ufs[root2];
_ufs[root2] = root1;
}
// 非压缩路径版本
//// 可以在边找的过程中,加一个压缩路径的过程
//int FindRoot(int index) // 找当前元素的根结点的下标
//{
// int parent = index; // 刚开始,每个元素都是一个独立的的根
// // 找根小于0的位置
// while (_ufs[parent] >= 0)
// {
// parent = _ufs[parent];
// }
// return parent;
//}
// 压缩路径版
int FindRoot(int index) // 找当前元素的根结点的下标
{
// 1. 找根 的下标
int root = index;
while (_ufs[root] >= 0)
{
root = _ufs[root];
}
// 2. 压缩路径
int cur = index;
while (_ufs[cur] >= 0)
{
int parent = _ufs[cur]; // 保存父亲
_ufs[cur] = root; // 将父亲改成跟
cur = parent; // 更新 cur
}
return root;
}
bool IsInSet(int index1, int index2) // 判断两个元素是否在同一个集合
{
int root1 = FindRoot(index1);
int root2 = FindRoot(index2);
return root1 == root2; // 两个元素有相同的根,则在同一个集合
}
// 数组中有几个值是负数,就有几个集合
size_t SetCount() const // 返回当前并查集中 集合的个数
{
size_t count = 0;
for (size_t i = 0; i < _ufs.size(); ++i)
{
if (_ufs[i] < 0)
++count;
}
return count;
}
private:
vector<int> _ufs;
};结语
并查集虽然结构简单,但它背后蕴含的思想却极其深刻:
用树形结构表达集合关系,用极低的代价解决高频的查询与合并问题。
从最初的"数组存父节点",到"按规模合并",再到"路径压缩"将时间复杂度优化到近似常数级,并查集的每一次优化,都体现了算法设计中"用空间换时间、用结构换效率"的核心思想。
在工程实践中,并查集并不仅仅存在于算法竞赛中:
- 网络连通性判断
- 最小生成树(Kruskal)
- 社交关系/朋友圈合并
- 动态连通图
- 等价关系建模
这些真实世界中的问题,本质上都可以抽象为"集合 + 关系 + 合并",而并查集正是解决这类问题的利器。
希望通过本文,你不仅掌握了并查集的实现方式,更重要的是理解了它的设计哲学
以上就是本文的所有内容了,如果觉得文章对你有帮助,欢迎 点赞⭐收藏 支持!如有疑问或建议,请在评论区留言交流,我们一起进步
分享到此结束啦
一键三连,好运连连!你的每一次互动,都是对作者最大的鼓励!
征程尚未结束,让我们在广阔的世界里继续前行!🚀