文章目录
- 一、引言
- 二、偏差修正篇
-
- [2.1 AGPO](#2.1 AGPO)
- [2.2 Dr.GRPO](#2.2 Dr.GRPO)
- [2.3 DARO](#2.3 DARO)
- 三、鲁棒优化篇
-
- [3.1 GMPO](#3.1 GMPO)
- [3.2 GEPO](#3.2 GEPO)
- [3.3 GRPO-MA](#3.3 GRPO-MA)
- [3.4 TEPO](#3.4 TEPO)
- 四、架构扩展篇
-
- [4.1 S-GRPO](#4.1 S-GRPO)
- [4.2 MGRPO](#4.2 MGRPO)
- 五、相关文章
一、引言
Group Relative Policy Optimization(GRPO)作为大语言模型强化学习的核心算法之一,通过组内相对优势估计消除了对价值网络的依赖,显著提升了训练效率。然而,随着研究的深入,GRPO 在理论严谨性、训练稳定性和能力边界等维度暴露出关键局限:一方面,长度归一化与标准差除法引入系统性偏差;另一方面,高方差梯度估计与脆弱的优势计算制约了大规模训练的稳定性。
针对这些挑战,研究者们从三个方向展开了改进:偏差修正方向聚焦于消除 GRPO 的理论缺陷,重构符合蒙特卡洛估计原理的优化目标;鲁棒优化方向致力于降低梯度方差、提升训练的鲁棒性与收敛效率;架构扩展方向则通过分层结构与序列组设计拓展模型的推理与自省能力。
本文梳理偏差修正、鲁棒优化、架构扩展三类演化方向的代表性工作(AGPO, Dr.GRPO, DARO, GMPO, GEPO, GRPO-MA, TEPO, S-GRPO, MGRPO),展现 GRPO 算法家族从"可用"到"好用"的进阶之路。
| 算法名称 | 发布时间 | 算法完整名称 | 论文链接 |
|---|---|---|---|
| AGPO | 2025.03 | Adaptive Group Policy Optimization | https://arxiv.org/abs/2503.15952 |
| Dr.GRPO | 2025.03 | Group Relative Policy Optimization Done Right | https://arxiv.org/abs/2503.20783 |
| S-GRPO | 2025.05 | Serial-Group Decaying-Reward Policy Optimization | https://arxiv.org/abs/2505.07686 |
| MGRPO | 2025.06 | Multi-layer Group Relative Policy Optimization | https://arxiv.org/abs/2506.04746 |
| GMPO | 2025.07 | Geometric-Mean Policy Optimization | https://arxiv.org/abs/2507.20673 |
| GEPO | 2025.08 | Group Expectation Policy Optimization | https://arxiv.org/abs/2508.17850 |
| GRPO-MA | 2025.09 | Group Relative Policy Optimization with Multi-Answer | https://arxiv.org/abs/2509.24494 |
| DARO | 2025.10 | Difficulty-Aware Reweighting Policy Optimization | https://arxiv.org/abs/2510.09001 |
| TEPO | 2025.10 | Token-Level Policy Optimization | https://arxiv.org/abs/2510.09369 |
二、偏差修正篇
2.1 AGPO
核心思想:通过自适应损失函数解决 GRPO 中的零优势和负损失问题。
- 损失掩码(Loss Mask): 当组内所有响应奖励相等(全对或全错)时,直接屏蔽该组的损失。
- 损失裁剪(Loss Clip): 解决正优势 → 负损失导致的过自信问题,将负损失裁剪为0,既不鼓励也不惩罚,保持探索性。
L ( q ) ∼ P ( Q ) = { masked , if { o i } i = 1 G all correct or wrong max ( 0 , − J GRPO ( θ ) ) , otherwise L_{(q) \sim P(Q)} = \begin{cases} \text{masked}, & \text{if } \{o_i\}{i=1}^{G} \text{ all correct or wrong} \\ \max(0, -J{\text{GRPO}}(\theta)), & \text{otherwise} \end{cases} L(q)∼P(Q)={masked,max(0,−JGRPO(θ)),if {oi}i=1G all correct or wrongotherwise
2.2 Dr.GRPO
核心思想:移除对回答长度和标准差的分母归一化,改为更符合理论的蒙特卡洛估计 + 全局批次级别的优势归一化。
- 长度偏差: GRPO 的损失函数被响应长度所除。这导致当模型回答错误时,它可以通过生成更长的、无关的废话来"稀释"惩罚,因为惩罚被分摊到了更多的词元上。
- 难度偏差 : 优势被奖励的标准差 s t d ( R ) std(R) std(R) 所除。这使得算法过于关注那些模型总能答对(太简单)或总答错(太难)的问题,因为这些问题的奖励方差小,优势绝对值大。
J D r . G R P O ( θ ) = 1 G ∑ i = 1 G 1 ∣ o i ∣ ∑ t = 1 ∣ o i ∣ { min [ π θ ( o i , t ∣ q , o i , < t ) π θ old ( o i , t ∣ q , o i , < t ) A ^ i , t , clip ( π θ ( o i , t ∣ q , o i , < t ) π θ old ( o i , t ∣ q , o i , < t ) , 1 − ε , 1 + ε ) A ^ i , t ] } \mathcal{J}{Dr.GRPO}(\theta) = \frac{1}{G} \sum{i=1}^{G} \textcolor{red}{\xcancel{\frac{1}{|\mathbf{o}i|}}} \sum{t=1}^{|\mathbf{o}i|} \left\{ \min\left[ \frac{\pi\theta(o_{i,t} \mid \mathbf{q}, \mathbf{o}{i,<t})}{\pi{\theta_{\text{old}}}(o_{i,t} \mid \mathbf{q}, \mathbf{o}{i,<t})} \hat{A}{i,t}, \quad \text{clip}\left( \frac{\pi_\theta(o_{i,t} \mid \mathbf{q}, \mathbf{o}{i,<t})}{\pi{\theta_{\text{old}}}(o_{i,t} \mid \mathbf{q}, \mathbf{o}{i,<t})}, 1-\varepsilon, 1+\varepsilon \right) \hat{A}{i,t} \right] \right\} JDr.GRPO(θ)=G1i=1∑G∣oi∣1 t=1∑∣oi∣{min[πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t)A^i,t,clip(πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t),1−ε,1+ε)A^i,t]}
w h e r e A ^ i , t = R ( q , o i ) − mean ( { R ( q , o 1 ) , ... , R ( q , o G ) } ) std ( { R ( q , o 1 ) , ... , R ( q , o G ) } ) where \quad \hat{A}_{i,t} = \frac{R(\mathbf{q}, \mathbf{o}_i) - \text{mean}\left( \{R(\mathbf{q}, \mathbf{o}_1), \ldots, R(\mathbf{q}, \mathbf{o}_G)\} \right)}{\textcolor{red}{\xcancel{\text{std}(\{R(\mathbf{q}, \mathbf{o}_1), \ldots, R(\mathbf{q}, \mathbf{o}_G)\})}}} whereA^i,t=std({R(q,o1),...,R(q,oG)}) R(q,oi)−mean({R(q,o1),...,R(q,oG)})
2.3 DARO
核心思想:将GRPO训练建模为多任务学习,通过可学习的动态权重机制自适应调节不同难度样本组的损失贡献,解决静态权重导致的损失尺度不平衡问题。
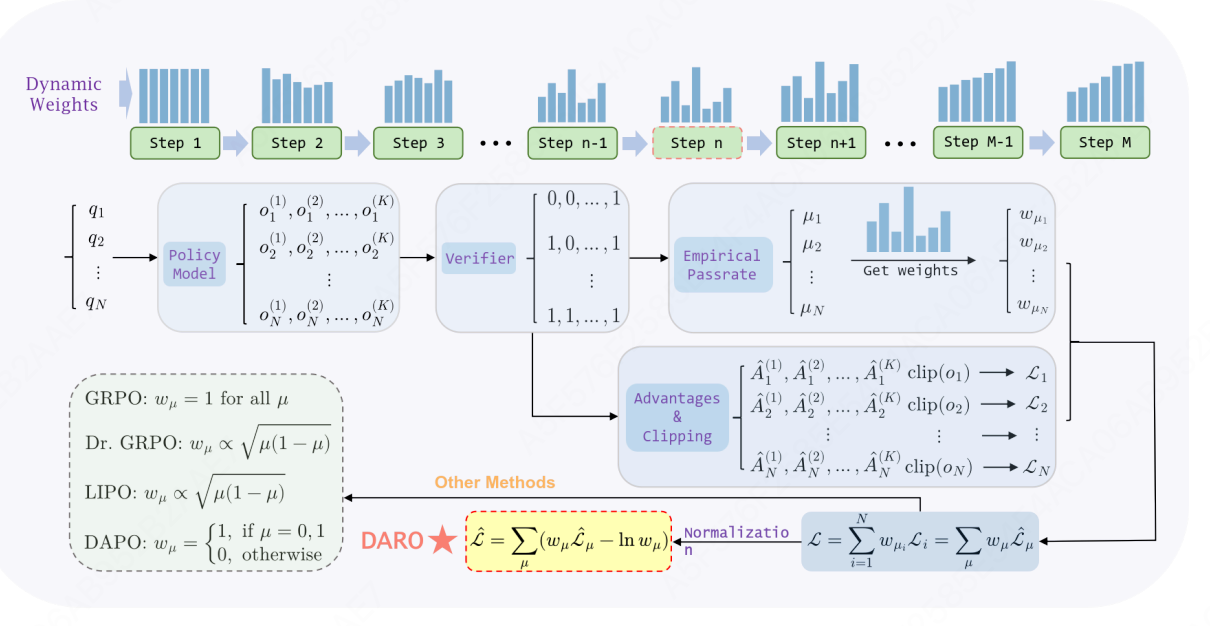
-
统一框架:将GRPO及其变体(DAPO、LIPO、Dr.GRPO)统一为带权重的损失形式:
L B A S E = E q ∼ Q , { o i } i = 1 K ∼ π θ o l d ( ⋅ ∣ q ) [ ∑ i = 1 K w i ⋅ ∣ o i ∣ L f ( A i , o i ) ] \mathcal{L}{BASE} = \mathbb{E}{q\sim\mathcal{Q},\{o_i\}{i=1}^K\sim\pi{\theta_{old}}(\cdot|q)}\left[\sum_{i=1}^K w_i \cdot \frac{|o_i|}{L} f(A_i, o_i)\right] LBASE=Eq∼Q,{oi}i=1K∼πθold(⋅∣q)[i=1∑Kwi⋅L∣oi∣f(Ai,oi)]
各方法的权重对比:
算法 权重 w i w_i wi 特性 GRPO w i = 1 w_i = 1 wi=1 均匀权重 DAPO w i = I ( 0 < μ < 1 ) w_i = \mathbb{I}(0<\mu<1) wi=I(0<μ<1) 二值过滤 LIPO/Dr.GRPO w i ∝ μ ( 1 − μ ) w_i \propto \sqrt{\mu(1-\mu)} wi∝μ(1−μ) 静态难度权重
损失尺度问题(Loss Scale Issue) :现有方法的权重由经验通过率 μ \mu μ 静态决定,导致训练过程中某些难度级别的样本损失占比过高,造成灾难性遗忘或探索不足。
-
动态难度感知重加权 :将不同 μ \mu μ 的样本组视为多任务,引入可学习的动态权重 w μ w_\mu wμ。
-
最终损失函数 :
L = ∑ μ ≠ 0 , 1 ( w μ L μ − ln w μ ) \mathcal{L} = \sum_{\mu \neq 0,1} \left(w_\mu \mathcal{L}\mu - \ln w\mu\right) L=μ=0,1∑(wμLμ−lnwμ)其中:
- L μ \mathcal{L}_\mu Lμ:经验通过率为 μ \mu μ 的样本组损失
- w μ w_\mu wμ:对应难度组的可学习权重参数
- − ln w μ -\ln w_\mu −lnwμ:正则化项,防止权重坍缩到零
-
权重更新机制 :通过梯度下降联合优化模型参数 θ \theta θ 和权重 w μ w_\mu wμ,使 w μ ∝ L μ − 1 w_\mu \propto \mathcal{L}_\mu^{-1} wμ∝Lμ−1,实现"损失大的组权重小,损失小的组权重大"的自适应平衡。
-
三、鲁棒优化篇
3.1 GMPO
核心思想:将 GRPO 的优化目标从最大化 token 级奖励的"算术平均"转为最大化其"几何平均"。
- 几何平均通过乘积与开方运算实现,能有效抑制极端大值的干扰,从而提供更为稳健、更具代表性的中心趋势度量。
- 借助几何平均的稳定性优势,GMPO 可采用更宽松的裁剪边界。经稳定性与探索效率的权衡,最终选择 ( e − 0.4 , e 0.4 ) (e^{-0.4}, e^{0.4}) (e−0.4,e0.4) 作为裁剪阈值。
J GMPO ( π θ ) = E q ∼ Q , { o i } i = 1 G ∼ π θ old ( ⋅ ∣ q ) 1 G ∑ i = 1 G { ∏ t = 1 ∣ o i ∣ ∣ min [ ρ i , t ( θ ) A ^ i , clip ( ρ i , t ( θ ) , ϵ low , ϵ high ) A ^ i ] ∣ } 1 ∣ o i ∣ ⋅ sgn ( A ^ i ) \mathcal{J}{\text{GMPO}}(\pi\theta) = \mathbb{E}{q \sim \mathcal{Q}, \{o_i\}{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot|q)} \frac{1}{G} \sum_{i=1}^{G} \left\{ \prod_{t=1}^{|o_i|} \left| \min \left[ \rho_{i,t}(\theta) \hat{A}i, \text{clip}(\rho{i,t}(\theta), \epsilon_{\text{low}}, \epsilon_{\text{high}}) \hat{A}_i \right] \right| \right\}^{\frac{1}{|o_i|}} \cdot \text{sgn}(\hat{A}_i) JGMPO(πθ)=Eq∼Q,{oi}i=1G∼πθold(⋅∣q)G1i=1∑G⎩ ⎨ ⎧t=1∏∣oi∣ min[ρi,t(θ)A^i,clip(ρi,t(θ),ϵlow,ϵhigh)A^i] ⎭ ⎬ ⎫∣oi∣1⋅sgn(A^i)
其中, ρ i , t ( θ ) = π θ ( o i , t ∣ q , o i , < t ) π θ old ( o i , t ∣ q , o i , < t ) \rho_{i,t}(\theta) = \frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t}|q,o_{i,<t})} ρi,t(θ)=πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t), sgn ( ⋅ ) \text{sgn}(·) sgn(⋅) 表示符号函数(确保优化方向)。
3.2 GEPO
核心思想:通过使用组期望加权来指数级降低重要性权重的方差,从而解决异步强化学习中训练不稳定问题。
组期望重要性权重(Group Expectation Importance Weight, GEIW) ,用当前提示 x x x 下的组期望概率 E ^ q [ q ( y ∣ x ) ] \widehat{\mathbb{E}}_{q}[q(y|x)] E q[q(y∣x)] 替代标准重要性权重 p ( y ∣ x ) q ( y ∣ x ) \frac{p(y|x)}{q(y|x)} q(y∣x)p(y∣x) 中的旧策略概率 q ( y ∣ x ) q(y|x) q(y∣x)。
w G E I W ( y ∣ x ) = p ( y ∣ x ) E ^ q [ q ( y ∣ x ) ] w_{\mathrm{GEIW}}(y|x) = \frac{p(y|x)}{\widehat{\mathbb{E}}_{q}[q(y|x)]} wGEIW(y∣x)=E q[q(y∣x)]p(y∣x)
对于每个输入 x x x,从 q ( ⋅ ∣ x ) q(\cdot|x) q(⋅∣x) 生成一组 G G G 个响应 { y 1 , ... , y G } \{y^1, \ldots, y^G\} {y1,...,yG} 形成采样组。由于 G G G 通常远小于完整策略空间,向量 ( q ( y 1 ∣ x ) , ... , q ( y G ∣ x ) ) (q(y^1|x), \ldots, q(y^G|x)) (q(y1∣x),...,q(yG∣x)) 不构成有效概率分布,简单使用算术平均会引入偏差。为获得更准确的估计,采用加权期望:
E ^ q [ q ( y ∣ x ) ] ≈ ∑ i = 1 G q ( y i ∣ x ) ^ ⋅ q ( y i ∣ x ) = ∑ i = 1 G q ( y i ∣ x ) 2 ∑ i = 1 G q ( y i ∣ x ) \widehat{\mathbb{E}}{q}[q(y|x)] \approx \sum{i=1}^{G} \widehat{q(y^i|x)} \cdot q(y^i|x) = \frac{\sum_{i=1}^{G} q(y^i|x)^2}{\sum_{i=1}^{G} q(y^i|x)} E q[q(y∣x)]≈i=1∑Gq(yi∣x) ⋅q(yi∣x)=∑i=1Gq(yi∣x)∑i=1Gq(yi∣x)2
其中 q ( y i ∣ x ) ^ = q ( y i ∣ x ) ∑ i = 1 G q ( y i ∣ x ) \widehat{q(y^i|x)} = \frac{q(y^i|x)}{\sum_{i=1}^{G} q(y^i|x)} q(yi∣x) =∑i=1Gq(yi∣x)q(yi∣x) 是组内归一化概率,作为每个 y i y^i yi 采样似然的经验估计。
GEPO 损失函数:
L G E P O i = min [ π θ ( y i ∣ x ) E π θ o l d ( ⋅ ∣ x ) [ π θ o l d ( y ∣ x ) ] A ^ i , c l i p 1 ± ϵ ( π θ ( y i ∣ x ) E π θ o l d ( ⋅ ∣ x ) [ π θ o l d ( y ∣ x ) ] ) A ^ i ] \mathcal{L}{\mathrm{GEPO}i} = \min\left[ \frac{\pi\theta(y^i|x)}{\mathbb{E}{\pi_{\theta_{old}}(\cdot|x)}[\pi_{\theta_{old}}(y|x)]} \hat{A}i, \ \mathrm{clip}{1\pm\epsilon}\left(\frac{\pi_\theta(y^i|x)}{\mathbb{E}{\pi{\theta_{old}}(\cdot|x)}[\pi_{\theta_{old}}(y|x)]}\right) \hat{A}_i \right] LGEPOi=min[Eπθold(⋅∣x)[πθold(y∣x)]πθ(yi∣x)A^i, clip1±ϵ(Eπθold(⋅∣x)[πθold(y∣x)]πθ(yi∣x))A^i]
其中组级优势估计为:
A ^ i = R ( x , y i ) − m e a n { R ( x , y 1 ) , ... , R ( x , y G ) } (Group Level) \hat{A}_i = R(x, y^i) - \mathrm{mean}\{R(x, y^1), \ldots, R(x, y^G)\} \quad \text{(Group Level)} A^i=R(x,yi)−mean{R(x,y1),...,R(x,yG)}(Group Level)
3.3 GRPO-MA
核心思想:对每个思维采样多个答案,用答案奖励的平均值估计思维价值,解耦思维与答案的梯度更新,降低优势估计方差,实现更稳定高效的训练。
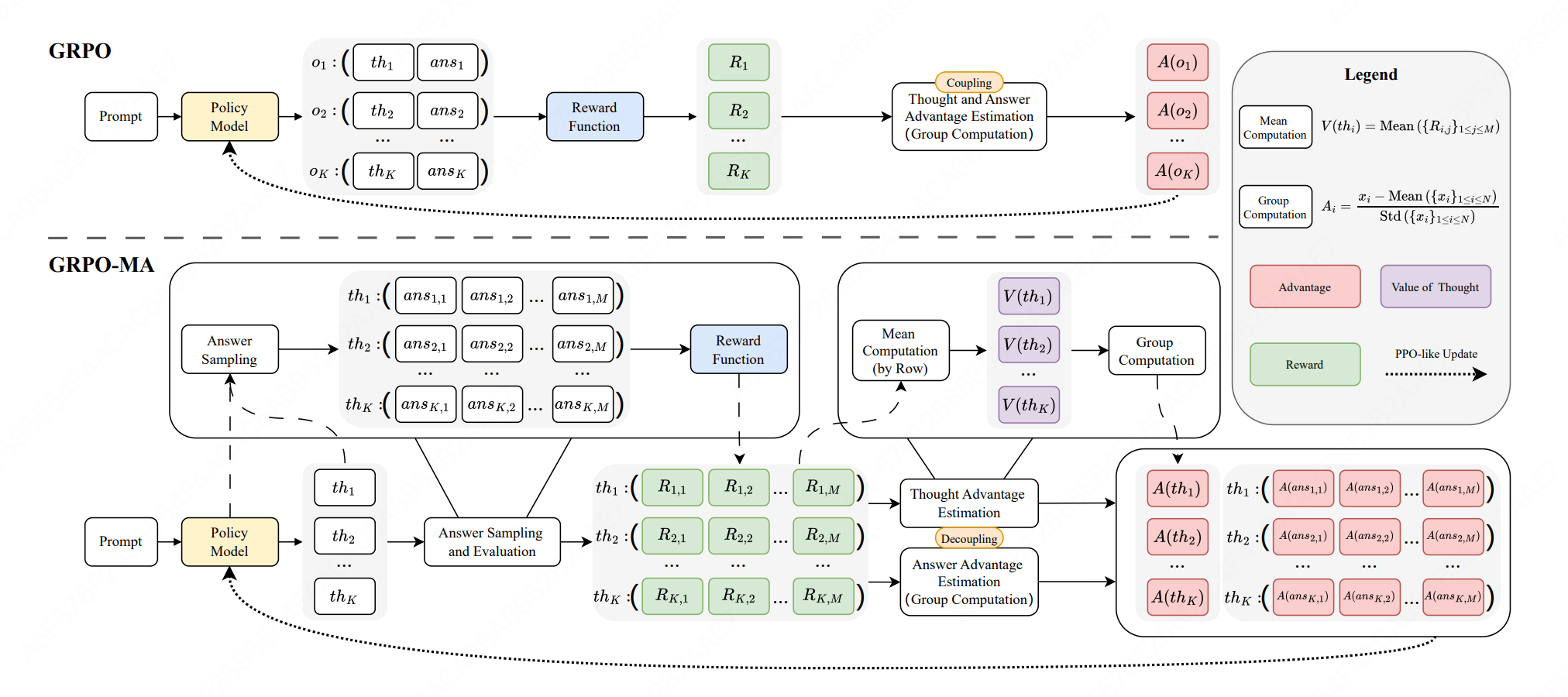
采样流程:
- 给定提示 p p p,首先生成 K K K 个思维 { t h 1 , ... , t h K } \{th_1, \ldots, th_K\} {th1,...,thK}
- 对每个思维 t h i th_i thi,生成 M M M 个答案 { a n s i , 1 , ... , a n s i , M } \{ans_{i,1}, \ldots, ans_{i,M}\} {ansi,1,...,ansi,M}
- 总共 K × M K \times M K×M 个答案,每 M M M 个答案共享同一个思维
思维价值与思维优势:
V ( t h i ) = 1 M ∑ j = 1 M R i , j V(th_i) = \frac{1}{M}\sum_{j=1}^{M}R_{i,j} V(thi)=M1j=1∑MRi,j
A ( t h i ) = V ( t h i ) − Mean ( { V ( t h k ) } 1 ≤ k ≤ K ) Std ( { V ( t h k ) } 1 ≤ k ≤ K ) A(th_i) = \frac{V(th_i) - \text{Mean}(\{V(th_k)\}{1 \leq k \leq K})}{\text{Std}(\{V(th_k)\}{1 \leq k \leq K})} A(thi)=Std({V(thk)}1≤k≤K)V(thi)−Mean({V(thk)}1≤k≤K)
答案优势:
A ( a n s i , j ) = R i , j − Mean ( { R k , l } 1 ≤ k ≤ K , 1 ≤ l ≤ M ) Std ( { R k , l } 1 ≤ k ≤ K , 1 ≤ l ≤ M ) A(ans_{i,j}) = \frac{R_{i,j} - \text{Mean}(\{R_{k,l}\}{1 \leq k \leq K, 1 \leq l \leq M})}{\text{Std}(\{R{k,l}\}_{1 \leq k \leq K, 1 \leq l \leq M})} A(ansi,j)=Std({Rk,l}1≤k≤K,1≤l≤M)Ri,j−Mean({Rk,l}1≤k≤K,1≤l≤M)
GRPO-MA 目标函数:
J G R P O − M A ( θ ) = E [ 1 K ∑ i = 1 K J c l i p ( θ , t h i ) + 1 K M ∑ i = 1 K ∑ j = 1 M J c l i p ( θ , a n s i , j ) ] \mathcal{J}{GRPO-MA}(\theta) = \mathbb{E}\left[\frac{1}{K}\sum{i=1}^{K}\mathcal{J}{clip}(\theta, th_i) + \frac{1}{KM}\sum{i=1}^{K}\sum_{j=1}^{M}\mathcal{J}{clip}(\theta, ans{i,j})\right] JGRPO−MA(θ)=E[K1i=1∑KJclip(θ,thi)+KM1i=1∑Kj=1∑MJclip(θ,ansi,j)]
- 第一项基于思维优势 A ( t h i ) A(th_i) A(thi) 更新策略(更新思维token)
- 第二项基于答案优势 A ( a n s i , j ) A(ans_{i,j}) A(ansi,j) 更新策略(更新答案token)
3.4 TEPO
核心思想:使用 Markov 似然将组级奖励转化为共享的序列级重要性比率,通过序列长度归一化实现 token 级梯度分配,以无熵正则化的方式实现稳定的 token 级策略优化。
标准 GRPO 每个 token 有独立的重要性权重 π θ ( y i , t ∣ x , y i , < t ) π θ o l d ( y i , t ∣ x , y i , < t ) \frac{\pi_\theta(y_{i,t}|x,y_{i,<t})}{\pi_{\theta_{old}}(y_{i,t}|x,y_{i,<t})} πθold(yi,t∣x,yi,<t)πθ(yi,t∣x,yi,<t),导致高方差。TEPO 使用共享的序列级(Markov 似然)重要性比率 I S i ( θ ) IS_i(\theta) ISi(θ),但通过以下方式实现 token 级优化:
∂ L ∂ π θ = ∂ L ∂ I S i ⋅ I S i ⏟ 批次级信号(组级奖励) ⋅ m a s k i , t ∣ o i ∣ ⋅ π θ ( θ ) ⏟ 序列归一化的 token 级信号 \frac{\partial \mathcal{L}}{\partial \pi_\theta} = \underbrace{\frac{\partial \mathcal{L}}{\partial IS_i} \cdot IS_i}{\text{批次级信号(组级奖励)}} \cdot \underbrace{\frac{\mathrm{mask}{i,t}}{|o_i| \cdot \pi_\theta(\theta)}}_{\text{序列归一化的 token 级信号}} ∂πθ∂L=批次级信号(组级奖励) ∂ISi∂L⋅ISi⋅序列归一化的 token 级信号 ∣oi∣⋅πθ(θ)maski,t
目标函数
L TEPO ( θ ) = 1 ∑ i = 1 G ∣ o i ∣ ∑ i = 1 G ∑ t = 1 ∣ o i ∣ min [ I S i ( θ ) A ^ i , t , c l i p ( I S i ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ i , t ] \mathcal{L}{\text{TEPO}}(\theta) = \frac{1}{\sum{i=1}^G |o_i|} \sum_{i=1}^G \sum_{t=1}^{|o_i|} \min\left[ IS_i(\theta) \hat{A}{i,t}, \mathrm{clip}(IS_i(\theta), 1-\epsilon, 1+\epsilon) \hat{A}{i,t} \right] LTEPO(θ)=∑i=1G∣oi∣1i=1∑Gt=1∑∣oi∣min[ISi(θ)A^i,t,clip(ISi(θ),1−ϵ,1+ϵ)A^i,t]
I S i ( θ ) = ( π θ ( y i ∣ x ) π θ o l d ( y i ∣ x ) ) 1 ∣ y i ∣ = exp ( 1 ∣ y i ∣ ∑ t = 1 ∣ y i ∣ log π θ ( y i , t ∣ x , y i , < t ) π θ o l d ( y i , t ∣ x , y i , < t ) ) IS_i(\theta) = \left( \frac{\pi_\theta(y_i|x)}{\pi_{\theta_{old}}(y_i|x)} \right)^{\frac{1}{|y_i|}} = \exp\left( \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \log \frac{\pi_\theta(y_{i,t}|x,y_{i,<t})}{\pi_{\theta_{old}}(y_{i,t}|x,y_{i,<t})} \right) ISi(θ)=(πθold(yi∣x)πθ(yi∣x))∣yi∣1=exp ∣yi∣1t=1∑∣yi∣logπθold(yi,t∣x,yi,<t)πθ(yi,t∣x,yi,<t)
- 约束条件: 0 < ∣ { o i ∣ is_equivalent ( a , o i ) } ∣ < G 0 < |\{o_i \mid \text{is\_equivalent}(a, o_i)\}| < G 0<∣{oi∣is_equivalent(a,oi)}∣<G
四、架构扩展篇
4.1 S-GRPO
核心思想:在单条推理路径上设置多个早退检查点形成"序列组",并对越早产生的正确答案给予指数级更高奖励,使模型学会在推理充分时及时终止思考,缩短推理长度。
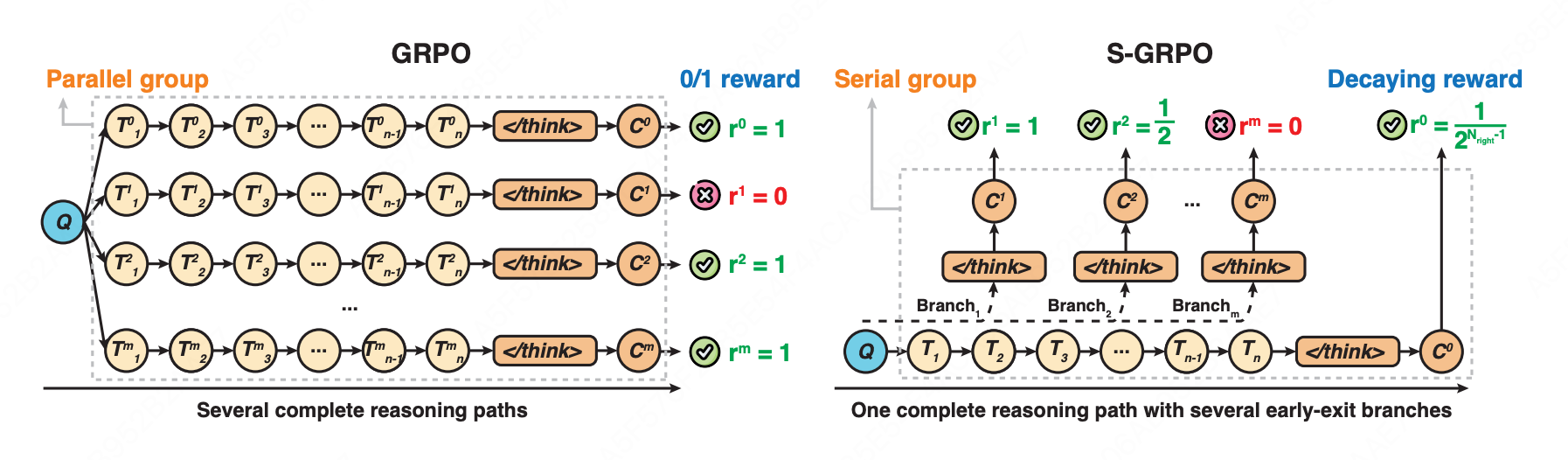
-
序列组生成
-
阶段一:Full Thought Rollout
- 生成完整推理路径: O 0 = { T 1 , T 2 , ... , T n , < / t h i n k > , C 0 } O^0 = \{T_1, T_2, \ldots, T_n, </think>, C_0\} O0={T1,T2,...,Tn,</think>,C0}
- 随机选择 m m m 个截断位置 P i ∼ Uniform ( 1 , n ) P_i \sim \text{Uniform}(1,n) Pi∼Uniform(1,n)
-
阶段二:Early-exit Thought Rollout
- 在每个截断位置 P i P_i Pi 插入提示词:"Time is limited, stop thinking and start answering.\n〈/think〉\n\n"
- 生成中间答案 C 1 , C 2 , ... , C m C_1, C_2, \ldots, C_m C1,C2,...,Cm,形成序列组 { O 1 , O 2 , ... , O m , O 0 } \{O^1, O^2, \ldots, O^m, O^0\} {O1,O2,...,Om,O0}
-
-
指数衰减奖励策略
r i = { 1 2 N right − 1 , if C i is correct 0 , if C i is incorrect r^i = \begin{cases} \frac{1}{2^{N_{\text{right}}-1}}, & \text{if } C^i \text{ is correct} \\ 0, & \text{if } C^i \text{ is incorrect} \end{cases} ri={2Nright−11,0,if Ci is correctif Ci is incorrect
其中 N right N_{\text{right}} Nright 表示当前位置为止累计的正确答案数量。越早退出且正确,奖励越高(1, 1/2, 1/4, 1/8...),错误答案一律得0。
目标函数
J S-GRPO ( θ ) = E q ∼ P ( Q ) , { o i } i = 1 G ∼ π θ old ( O ∣ q ) [ 1 G ∑ i = 1 G 1 ∣ o i ∣ ∑ t = 1 ∣ o i ∣ min [ π θ i , t π θ old i , t A ^ i , t , clip ( π θ i , t π θ old i , t , 1 − ϵ , 1 + ϵ ) A ^ i , t ] ] \mathcal{J}{\text{S-GRPO}}(\theta) = \mathbb{E}{q \sim P(Q), \{o_i\}{i=1}^G \sim \pi{\theta_{\text{old}}}(O|q)} \left[ \frac{1}{G}\sum_{i=1}^{G} \frac{1}{|o_i|}\sum_{t=1}^{|o_i|} \min\left[\frac{\pi_\theta^{i,t}}{\pi_{\theta_{\text{old}}}^{i,t}}\hat{A}{i,t}, \text{clip}\left(\frac{\pi\theta^{i,t}}{\pi_{\theta_{\text{old}}}^{i,t}}, 1-\epsilon, 1+\epsilon\right)\hat{A}_{i,t}\right] \right] JS-GRPO(θ)=Eq∼P(Q),{oi}i=1G∼πθold(O∣q) G1i=1∑G∣oi∣1t=1∑∣oi∣min[πθoldi,tπθi,tA^i,t,clip(πθoldi,tπθi,t,1−ϵ,1+ϵ)A^i,t]
A ^ i = r i − mean ( r i ) \hat{A}_i = r_i - \text{mean}(r_i) A^i=ri−mean(ri)
4.2 MGRPO
核心思想:在标准 GRPO 框架的基础上引入了两层结构,提升模型的推理和自我纠正能力。
Layer 1:初始响应生成
策略 π θ o l d \pi_{\theta_{old}} πθold 生成 G G G 个响应 { o 1 , ... , o G } \{o_1, \ldots, o_G\} {o1,...,oG},规则验证器分配奖励 R ( o i ) R(o_i) R(oi),使用标准GRPO更新策略。
Layer 2:自我纠错与优化
-
Step 1: 修正(Correction)
对每个Layer 1的响应 o i o_i oi(包含思维过程 t h o u g h t i thought_i thoughti 和答案 a n s i ans_i ansi),构造Layer 2的增强查询:
q i ′ = SystemPrompt L 2 + User: [ q ] + Assistant: [ < t h i n k > t h o u g h t i < / t h i n k > a n s i ] + p g u i d e q_i' = \text{SystemPrompt}{L2} + \text{User:}[q] + \text{Assistant:}[<think>thought_i</think>ans_i] + p{guide} qi′=SystemPromptL2+User:[q]+Assistant:[<think>thoughti</think>ansi]+pguide
-
Step 2: 增强(Augmentation)
对每个 q i ′ q_i' qi′,模型 π θ o l d \pi_{\theta_{old}} πθold 生成 H H H 个候选修正响应 { o ~ i , 1 , ... , o ~ i , H } \{\tilde{o}{i,1}, \ldots, \tilde{o}{i,H}\} {o~i,1,...,o~i,H},用于收集多种纠错尝试,增强学习信号。
-
Step 3: 选择(Selection)
动态验证每个修正响应 o ~ i , j \tilde{o}_{i,j} o~i,j:
Layer 1状态 Layer 2状态 结果类型 错误 ( o i o_i oi) 正确 ( o ~ i , j \tilde{o}_{i,j} o~i,j) 成功纠错 正确 ( o i o_i oi) 正确 ( o ~ i , j \tilde{o}_{i,j} o~i,j) 成功确认 正确 ( o i o_i oi) 错误 ( o ~ i , j \tilde{o}_{i,j} o~i,j) 丢弃 错误 ( o i o_i oi) 错误 ( o ~ i , j \tilde{o}_{i,j} o~i,j) 丢弃 若 o i o_i oi 错误且所有 H H H 个修正响应均错误,则该轨迹不参与Layer 2梯度更新。
策略更新: π θ \pi_\theta πθ 接收来自两层的梯度,统一优化。
- Layer 1 梯度 → 提升直接求解能力
- Layer 2 梯度 → 提升自我纠错能力
J Layer1-GRPO ( θ ) = E q ∼ P ( Q ) , { o i } i = 1 G ∼ π θ o l d ( O ∣ q ) [ 1 G ∑ i = 1 G 1 ∣ o i ∣ ∑ t = 1 ∣ o i ∣ min ( r i , t ( L 1 ) ( θ ) A ^ i , t ( L 1 ) , clip ( r i , t ( L 1 ) ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ i , t ( L 1 ) ) − β D K L ( π θ ∥ π r e f ) ] \mathcal{J}{\text{Layer1-GRPO}}(\theta) = \mathbb{E}{q \sim P(Q), \{o_i\}{i=1}^G \sim \pi{\theta_{old}}(O|q)} \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \min\left( r_{i,t}^{(L1)}(\theta) \hat{A}{i,t}^{(L1)}, \text{clip}(r{i,t}^{(L1)}(\theta), 1-\epsilon, 1+\epsilon) \hat{A}{i,t}^{(L1)} \right) - \beta \mathbb{D}{KL}(\pi_\theta \| \pi_{ref}) \right] JLayer1-GRPO(θ)=Eq∼P(Q),{oi}i=1G∼πθold(O∣q) G1i=1∑G∣oi∣1t=1∑∣oi∣min(ri,t(L1)(θ)A^i,t(L1),clip(ri,t(L1)(θ),1−ϵ,1+ϵ)A^i,t(L1))−βDKL(πθ∥πref)
J Layer2-GRPO ( θ ) = E q ′ ∼ P ( Q ′ ) , { o ~ j ( h ) } h = 1 H ∼ π θ o l d ( O ∣ q ′ ) [ 1 H ∑ j = 1 G ′ ∑ h = 1 H 1 ∣ o ~ j ( h ) ∣ ∑ t = 1 ∣ o ~ j ( h ) ∣ min ( r ~ j , t ( h ) ( θ ) A ^ j , t ( h ) , clip ( r ~ j , t ( h ) ( θ ) , 1 − ϵ , 1 + ϵ ) A ^ j , t ( h ) ) − β D K L ( π θ ∥ π r e f ) ] \mathcal{J}{\text{Layer2-GRPO}}(\theta) = \mathbb{E}{q' \sim P(Q'), \{\tilde{o}j^{(h)}\}{h=1}^H \sim \pi_{\theta_{old}}(O|q')} \left[ \frac{1}{H} \sum_{j=1}^{G'} \sum_{h=1}^H \frac{1}{|\tilde{o}j^{(h)}|} \sum{t=1}^{|\tilde{o}j^{(h)}|} \min\left( \tilde{r}{j,t}^{(h)}(\theta) \hat{A}{j,t}^{(h)}, \text{clip}(\tilde{r}{j,t}^{(h)}(\theta), 1-\epsilon, 1+\epsilon) \hat{A}{j,t}^{(h)} \right) - \beta \mathbb{D}{KL}(\pi_\theta \| \pi_{ref}) \right] JLayer2-GRPO(θ)=Eq′∼P(Q′),{o~j(h)}h=1H∼πθold(O∣q′) H1j=1∑G′h=1∑H∣o~j(h)∣1t=1∑∣o~j(h)∣min(r~j,t(h)(θ)A^j,t(h),clip(r~j,t(h)(θ),1−ϵ,1+ϵ)A^j,t(h))−βDKL(πθ∥πref)