【你奶奶都能听懂的算法数据结构】 第14 期 数据结构
目录
- 一.树
- 二.二叉树
- 三.堆
- 四.红黑树
- 五.哈希表
开头:
ok,我们书接上回,上一期我们学习了在算法竞赛中数据结构相关的知识,一起学习了顺序表、链表、双向链表、栈、队列这几个数据结构。今天我们来学习下半部分,内容包括:树、二叉树、堆、红黑树、哈希表这几个数据结构
一.树
在学习篇中我们已经超详细的讲解了树相关的知识,这里补充两点:
- 有序树 / 无序树
• 有序树:结点的⼦树按照从左往右的顺序排列,不能更改。
• ⽆序树:结点的⼦树之间没有顺序,随意更改。
所谓的无序树简单来说就是,一棵树上下关系保证不变,同一层的节点顺序可以更换
- 有根树 / 无根树
• 有根树:树的根节点已知,是固定的。
• ⽆根树:树的根节点未知,谁都可以是根结点。
在竞赛中一般的树形结构是一个无序、无根树
1.实现方式
对于树的存储方式,现阶段我们只需要掌握孩子表示法,因为是一个无根树,我们存储时要把每一个元素的孩子节点都存起来,有两种方法:vector数组、链式前向星
题目会这样描述;

如上图,只会告诉你那两个节点之间有连接,但是父子关系未知,就是个典型的无根树,所以我们要将两个节点的信息都存储起来
-
vector数组
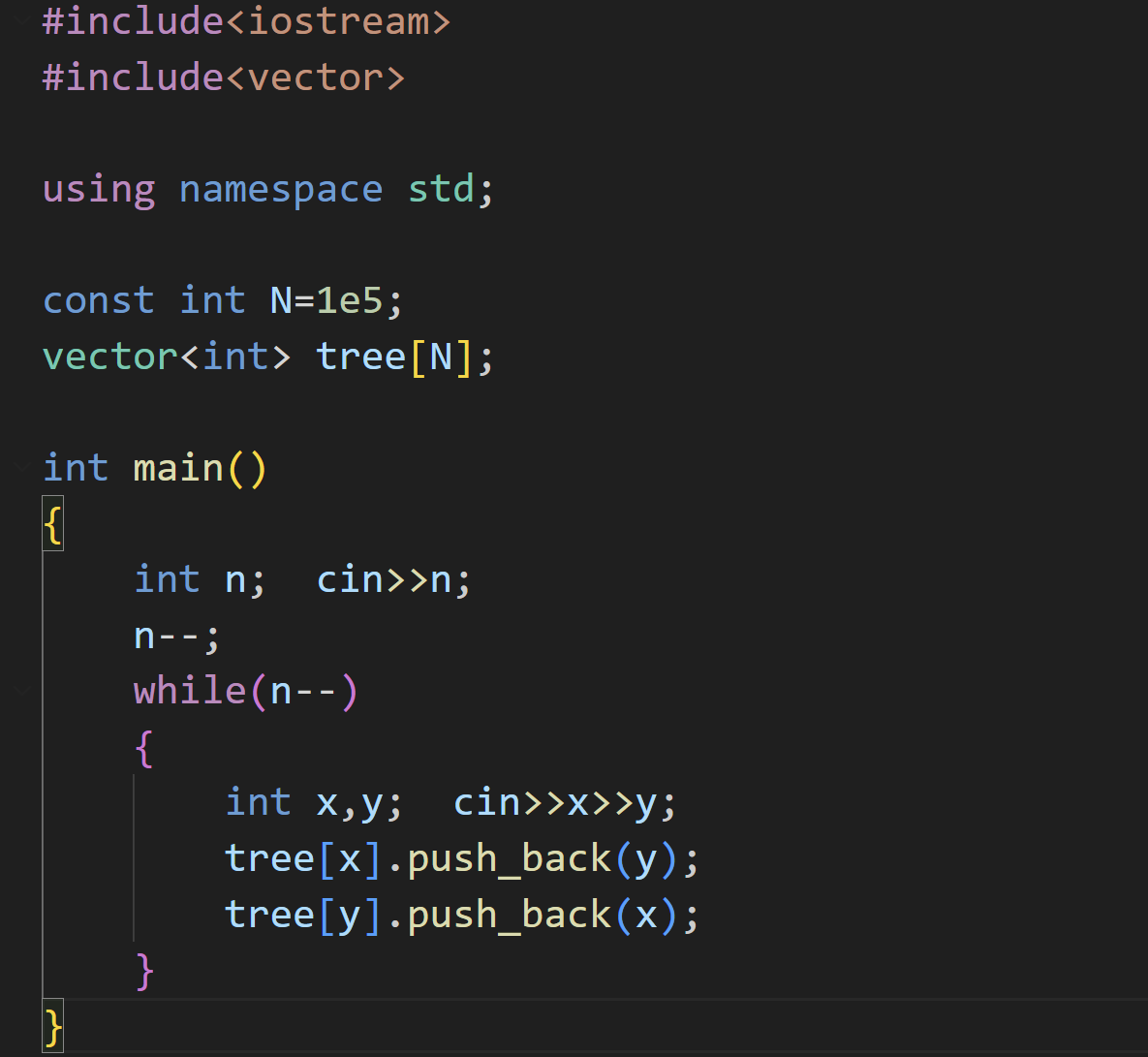
-
链式前向星
所谓的链式前向星,就是用数组来模拟一组链表,将对应的关系直接头插在后面
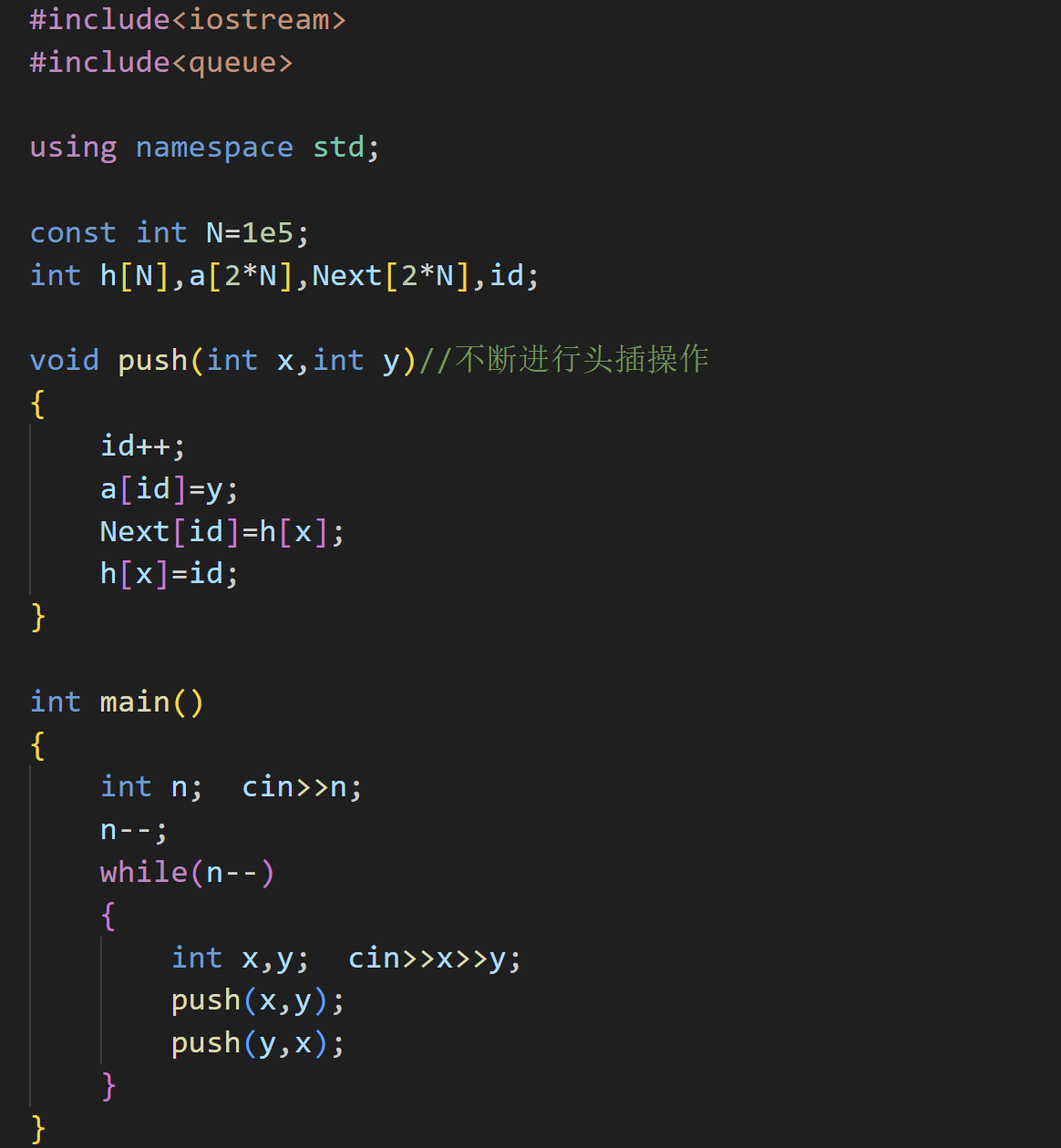
要注意的是,这里的数据域和指针域是节点数的2倍,因为存储的是双向关系
2.树的遍历
树的遍历就是不重不漏的将树中所有的点都扫描⼀遍。
常⽤的遍历方式有两种,⼀种是深度优先遍历,另⼀种是宽度优先遍历
这里我们重点是要学习用 vector数组以及链式前向星的方式存储的数组如何进行遍历
(1)深度优先遍历------DFS
具体流程:
- 从根节点出发,依次遍历每⼀棵⼦树;
- 遍历⼦树的时候,重复第⼀步。
就是我们在学习篇中学习的前序、中序、后序遍历------二叉树
vector 数组
因为在存储节点的时候我们是双向存储的,为了避免重复遍历,要使用一个布尔数组来记录一个节点是否被遍历,也是用递归来实现的
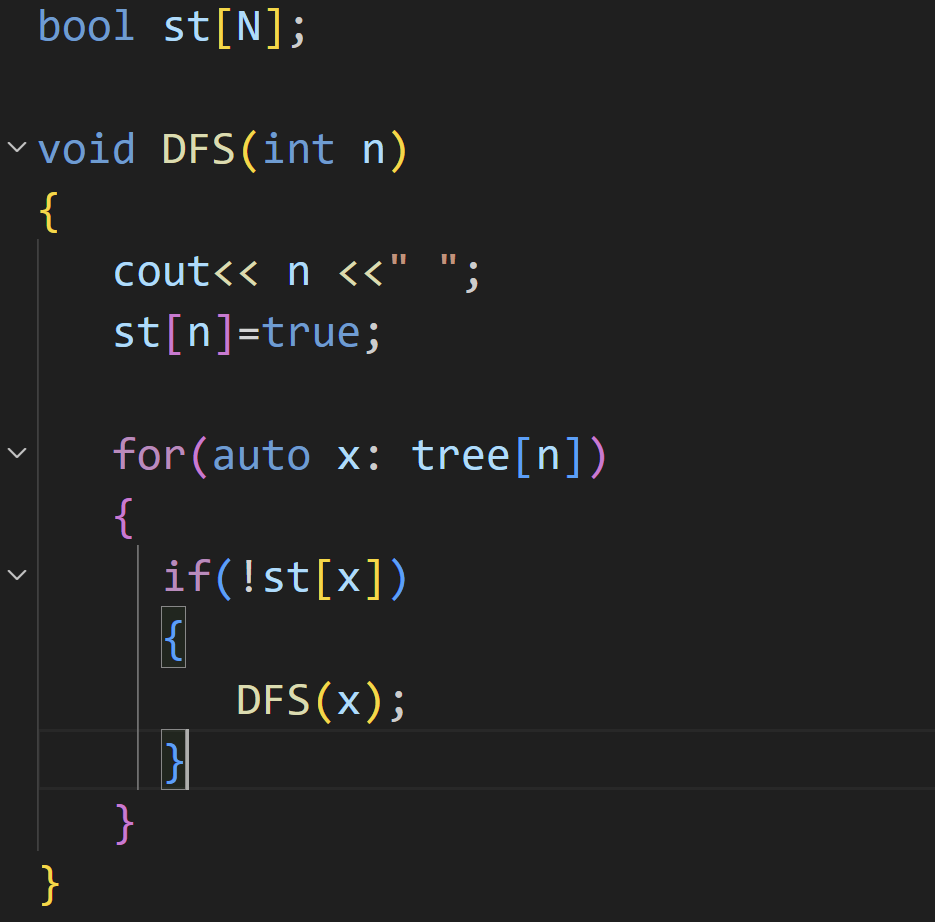
首先先输出对应的节点,然后将这个节点在布尔数组里面标记为真,表示此节点已经被访问过了,接着就是遍历这个节点的孩子节点,判断其是否被遍历过,如果未被遍历,那就调用自身函数
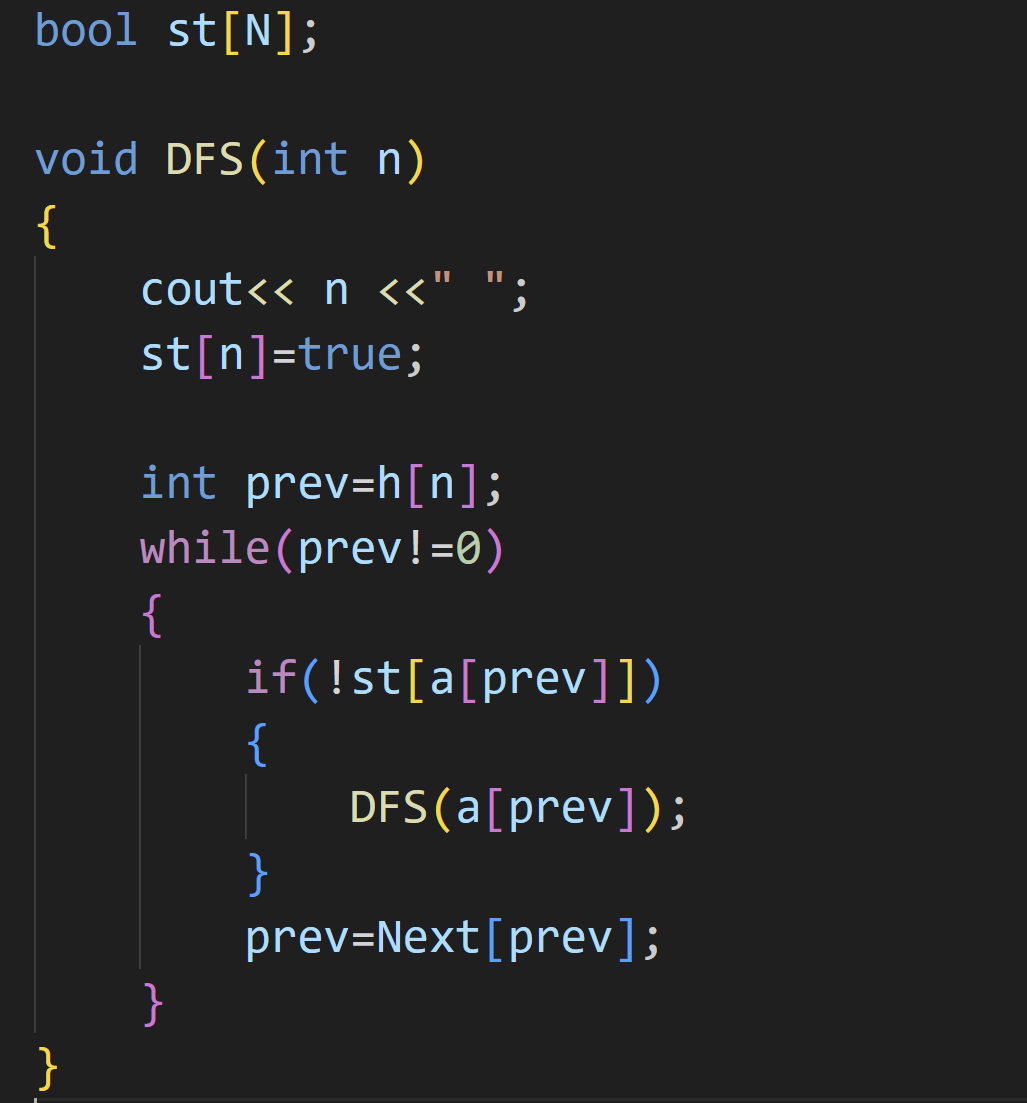
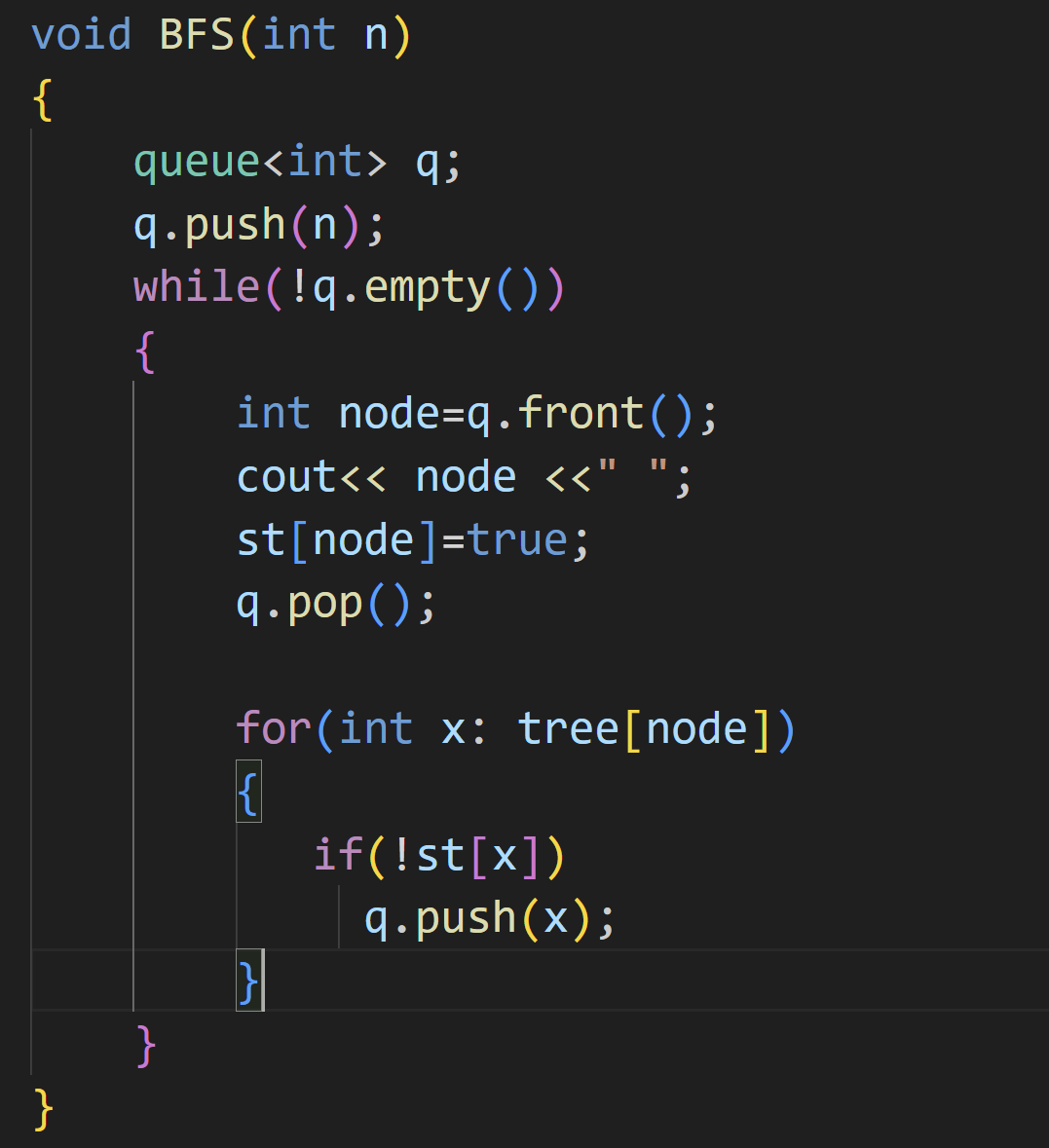
链式前向星
和上面的思路一样,都要先标记节点,然后遍历与其相连的孩子
(2)宽度优先遍历------BFS
所谓宽度优先。就是每次都尝试访问同⼀层的节点。 如果同⼀层都访问完
了,再访问下⼀层。
BFS先前的学习篇也学习过,要借助队列这个数据结构
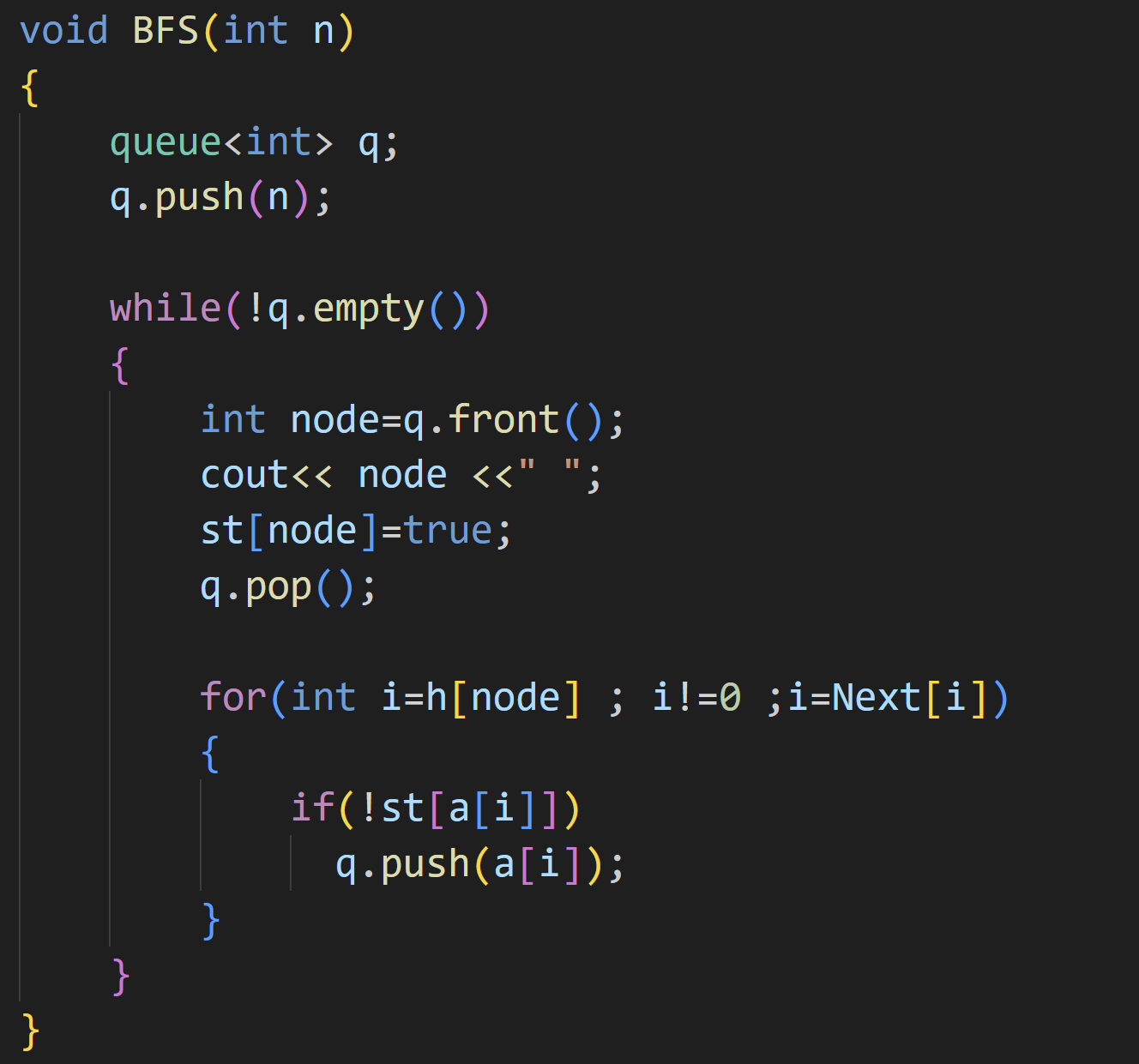
vector数组
链式前向星
3.例题
因为涉及树的算法题比较难
树的题我们以后再探索吧【狗头】
二.二叉树
关于二叉树相关知识的学习在这里------全站最详细二叉树讲解
这里直接来看模拟实现
1.实现方式
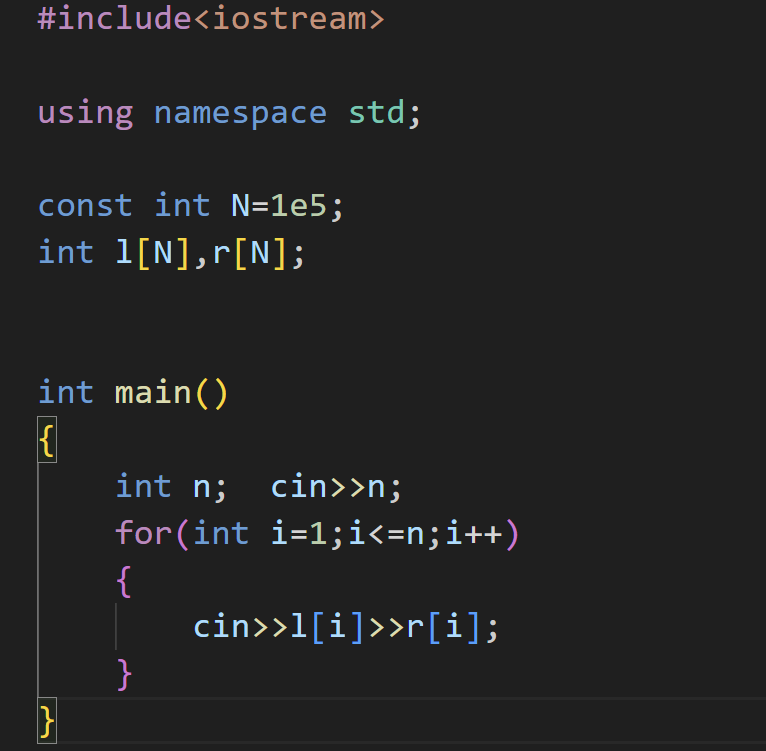
二叉树的模拟实现十分的简单,就是定义两个数组,l 和 r 分别来存储对应编号的左右孩子节点的编号
2.二叉树的遍历
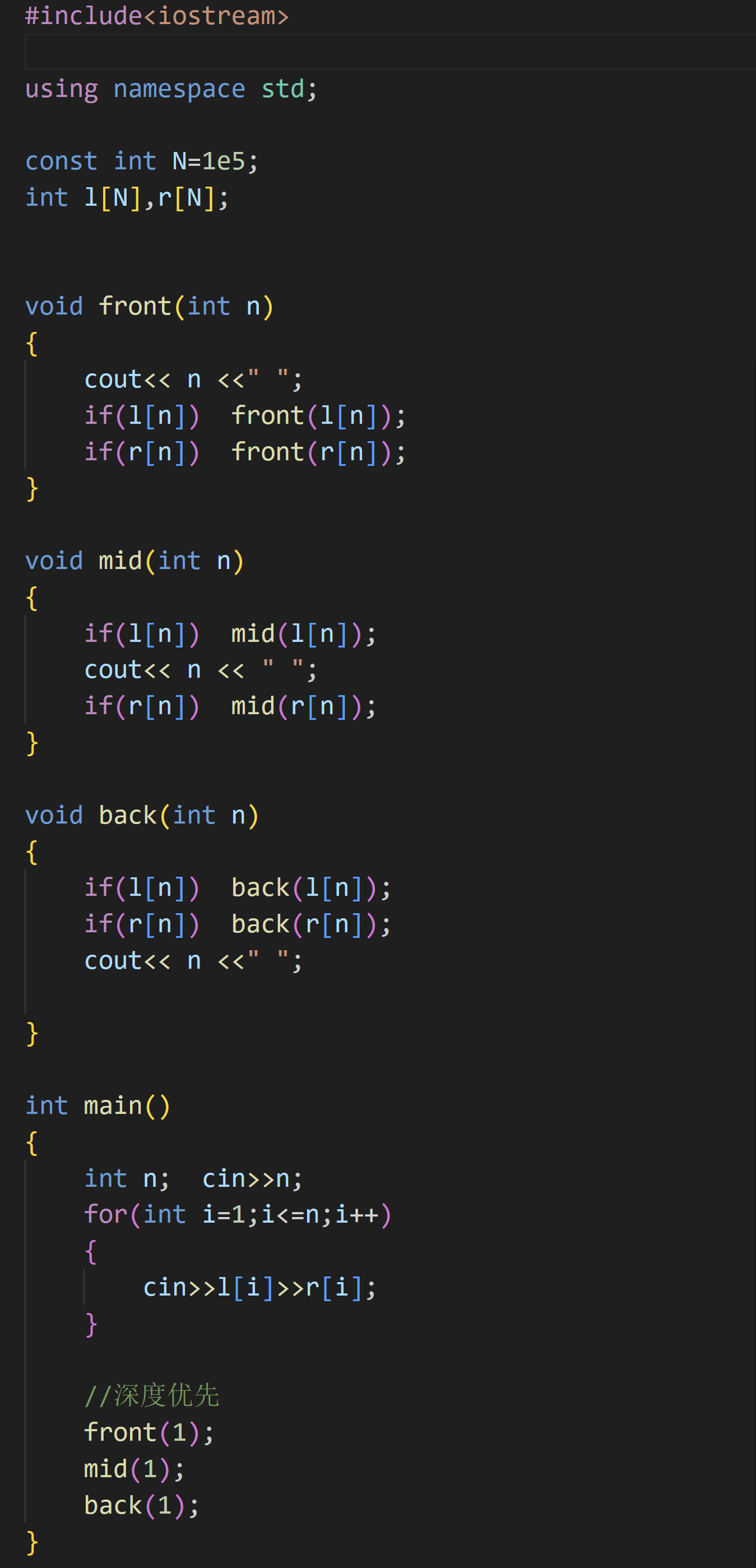
(1)深度优先遍历
不同于常规树的深度优先遍历,⼆叉树因其独特的性质可以划分成三种深度优先遍历:先序遍历,中
序遍历,和后序遍历。其中,三种遍历⽅式的不同在于处理根节点的时机。
对于⼀棵⼆叉树⽽⾔,整体可以划分成三部分:根节点 + 左⼦树 + 右⼦树:
• 先序遍历的顺序为:根 + 左 + 右;
• 中序遍历的顺序为:左 + 根 + 右;
• 后序遍历的顺序为:左 + 右 + 根。
(2)宽度优先遍历
依旧是要借助队列

3.例题
(1)新二叉树
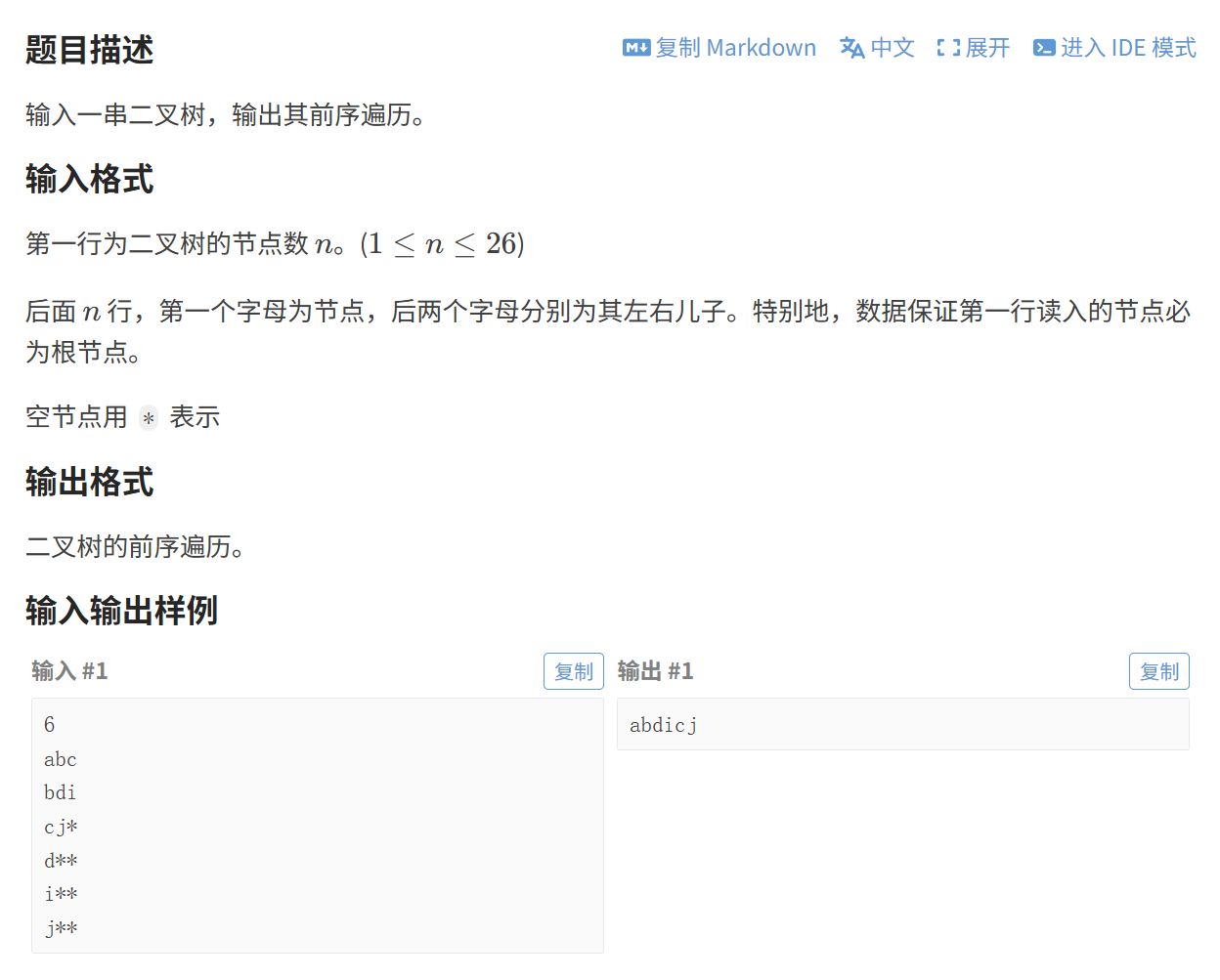
一道基础题,就是考察二叉树的前序遍历
代码实现:
(2)二叉树的高度
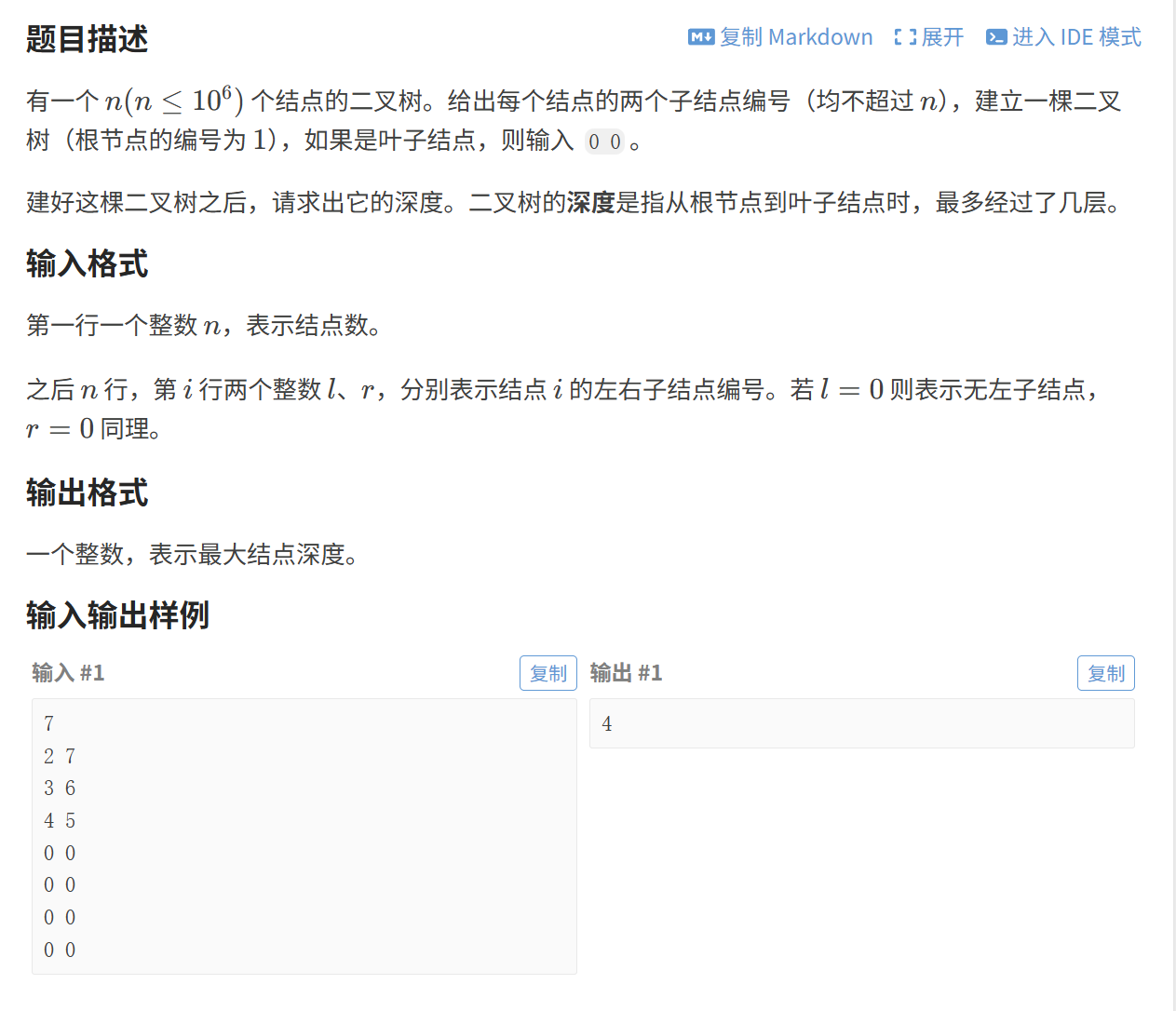
依旧是模板题,直接给出代码:
代码实现:
(3)已知中、后序推前序
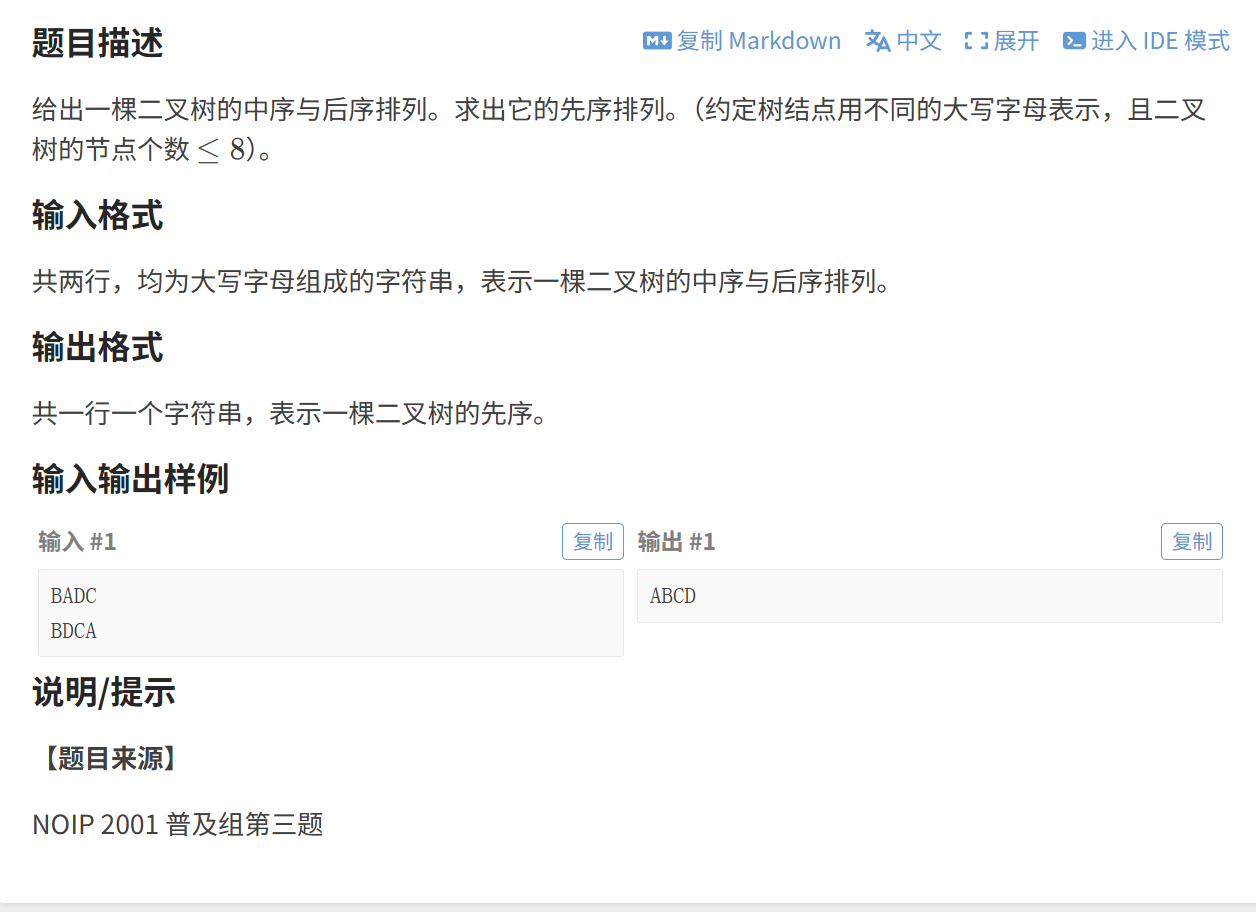
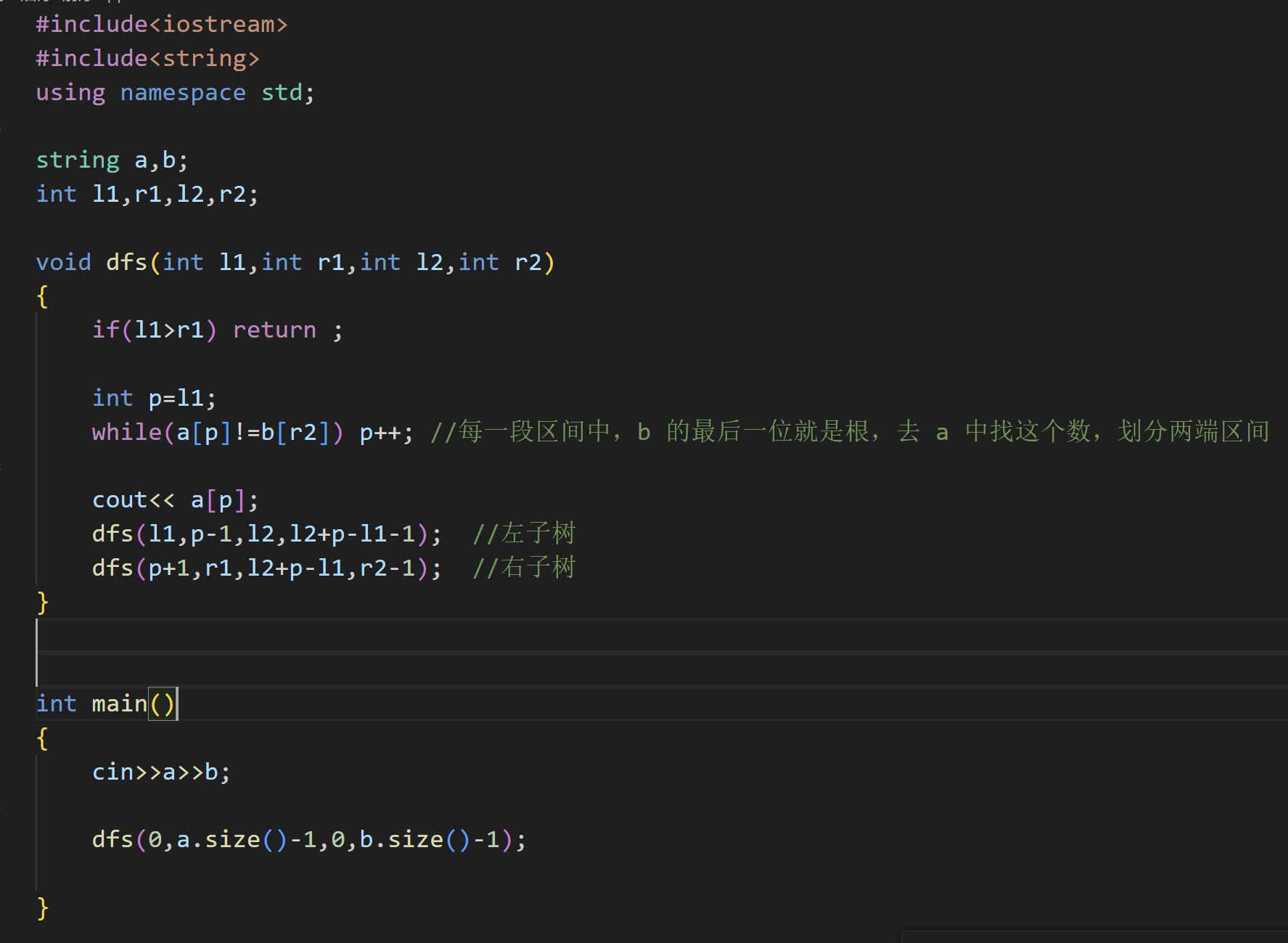
我们知道,中序遍历是按照:左子树、根、右子树 的顺序进行遍历,而后序遍历是按照:左子树、右子树、根 进行遍历
,这样就可以先根据后序遍历的结果将 根节点找到,将中序遍历的结果按照根节点分成左右两个部分
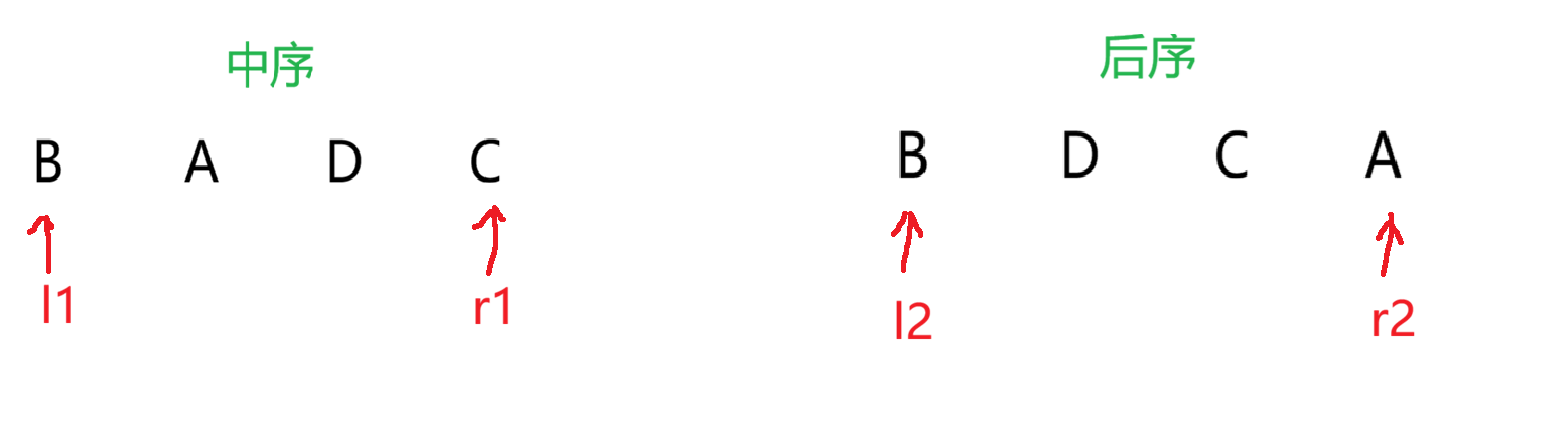
首先定义四个指针,分别指向两个字符串的首尾,此时 r2 指向的就是一个根节点,接着我们遍历中序的字符串,找到 r2 指向的 A 并将数组分成两个部分
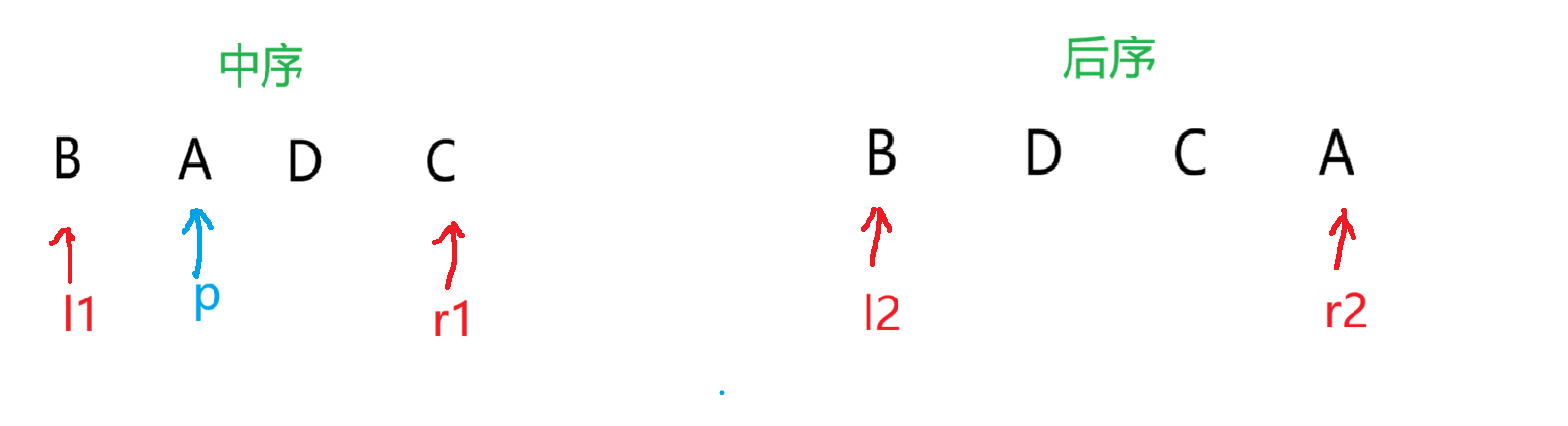
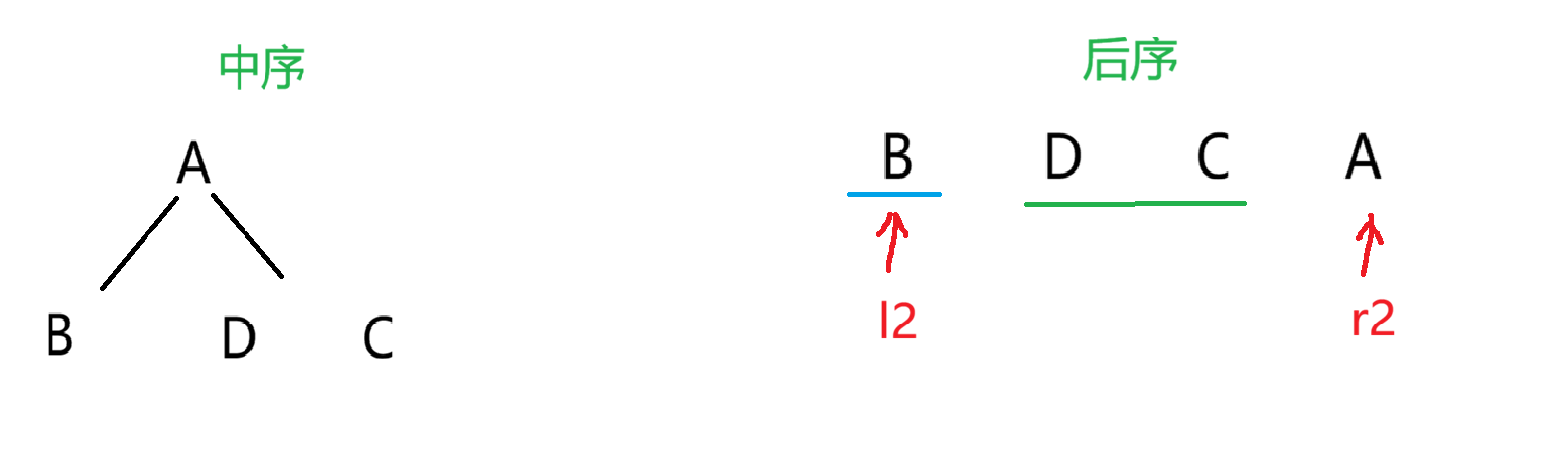
接着继续重复上述操作,用递归来实现
代码实现:
(3)已知中、前序推后序
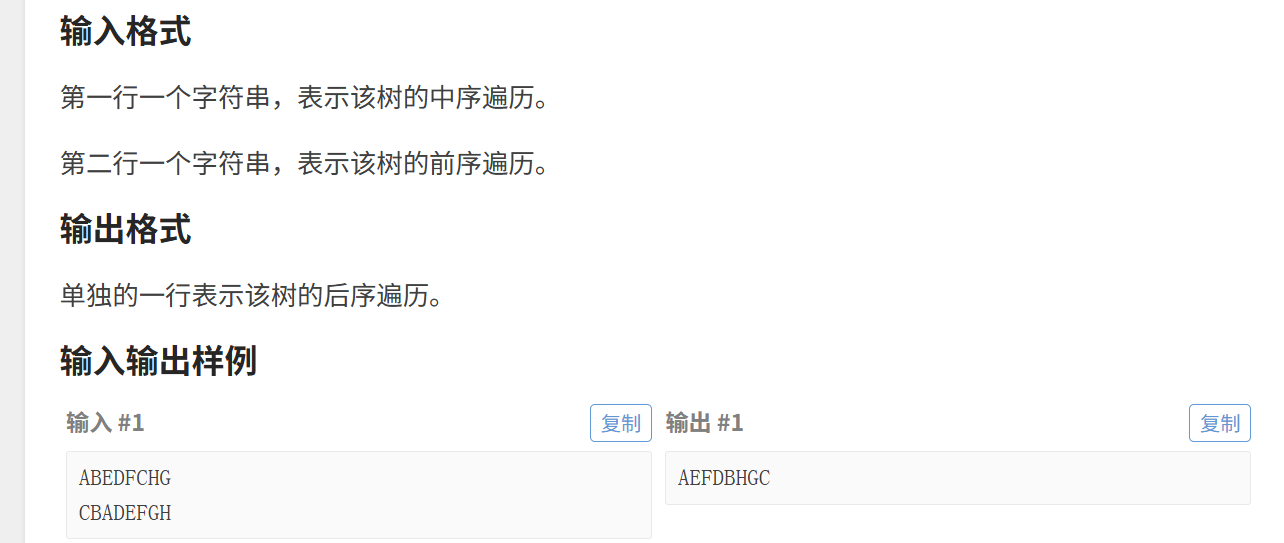
思路和上面的一摸一样
代码展示:
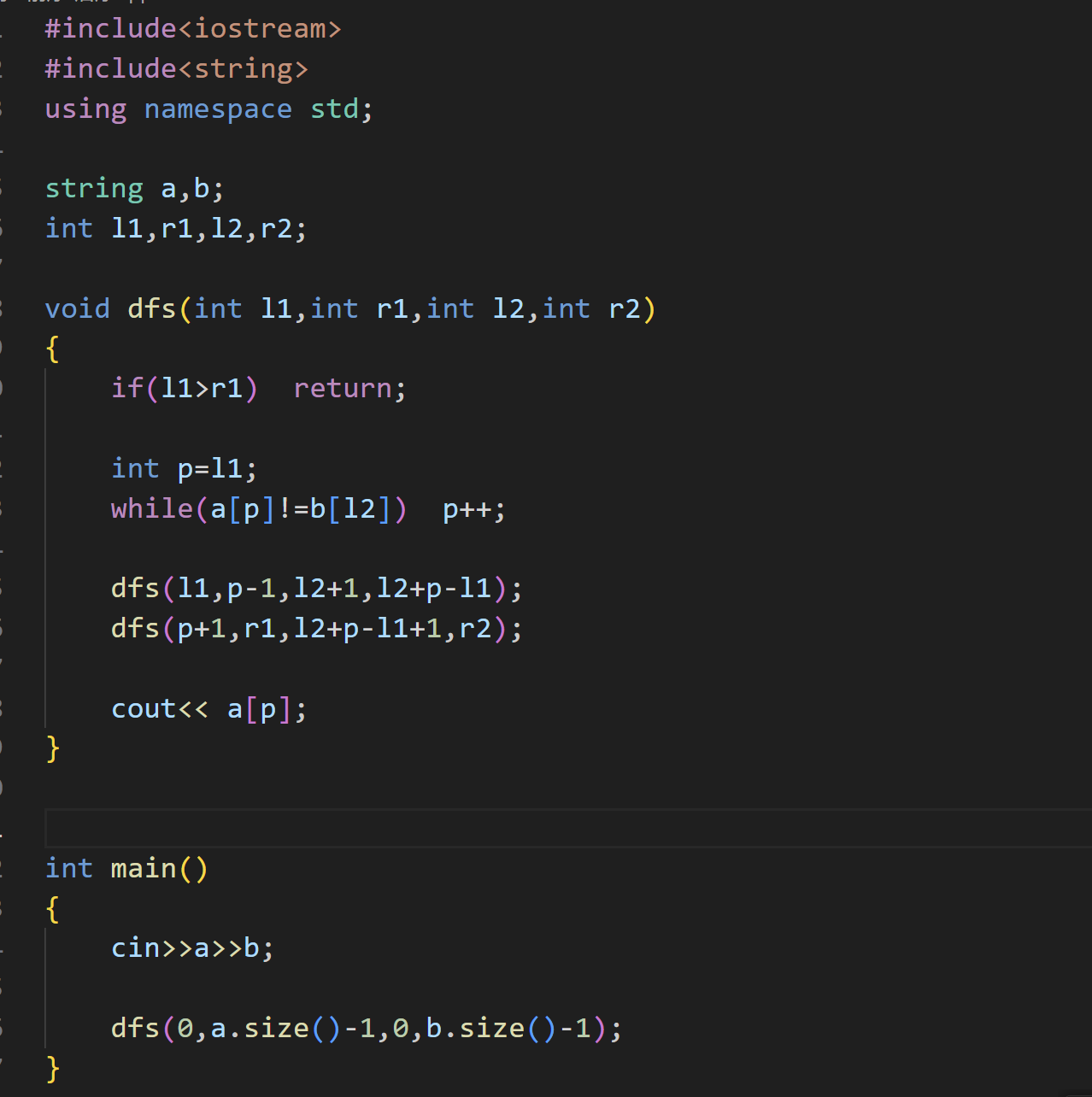
(4)二叉树问题

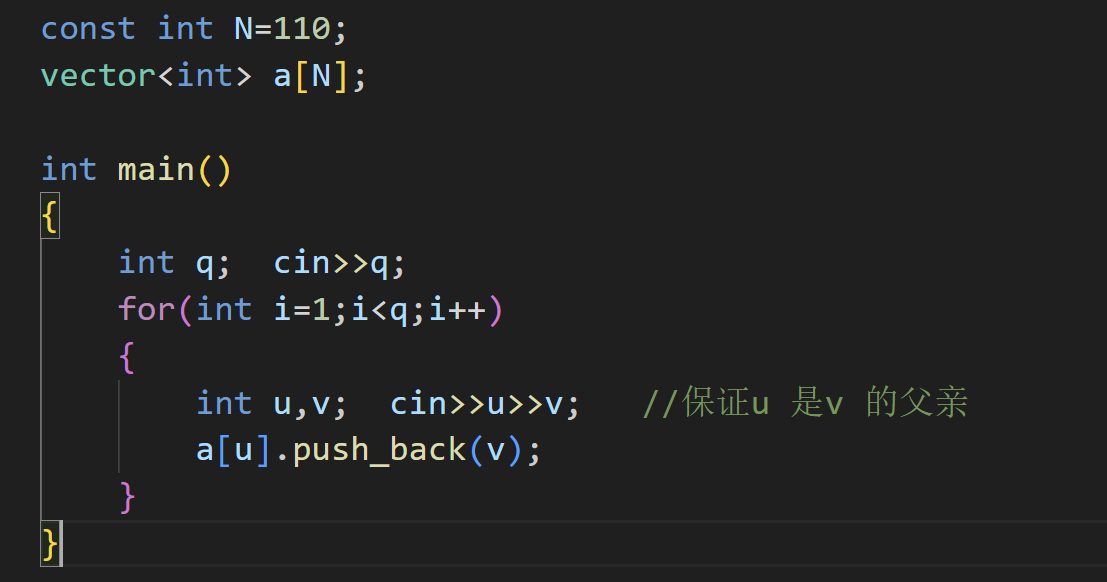
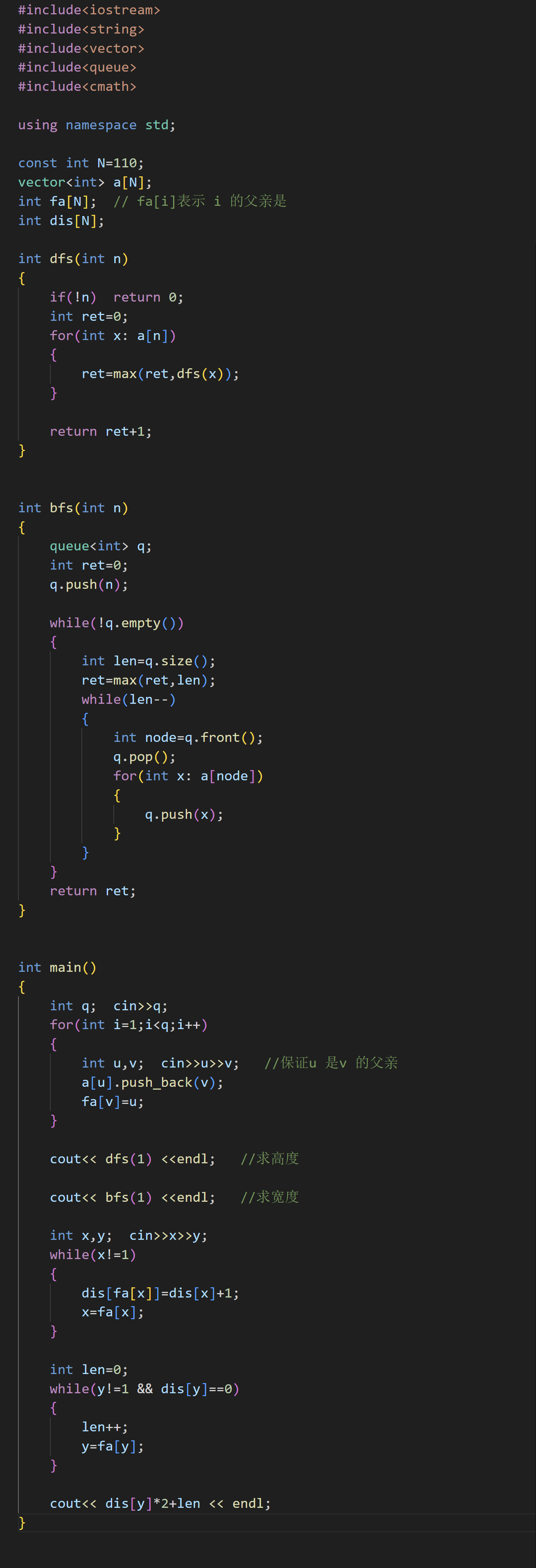
这是一道非常综合的考察二叉树的例题,我们一步步来解决
要注意的地方是:题目中保证 u 是 v 的父节点
问题1:求树高
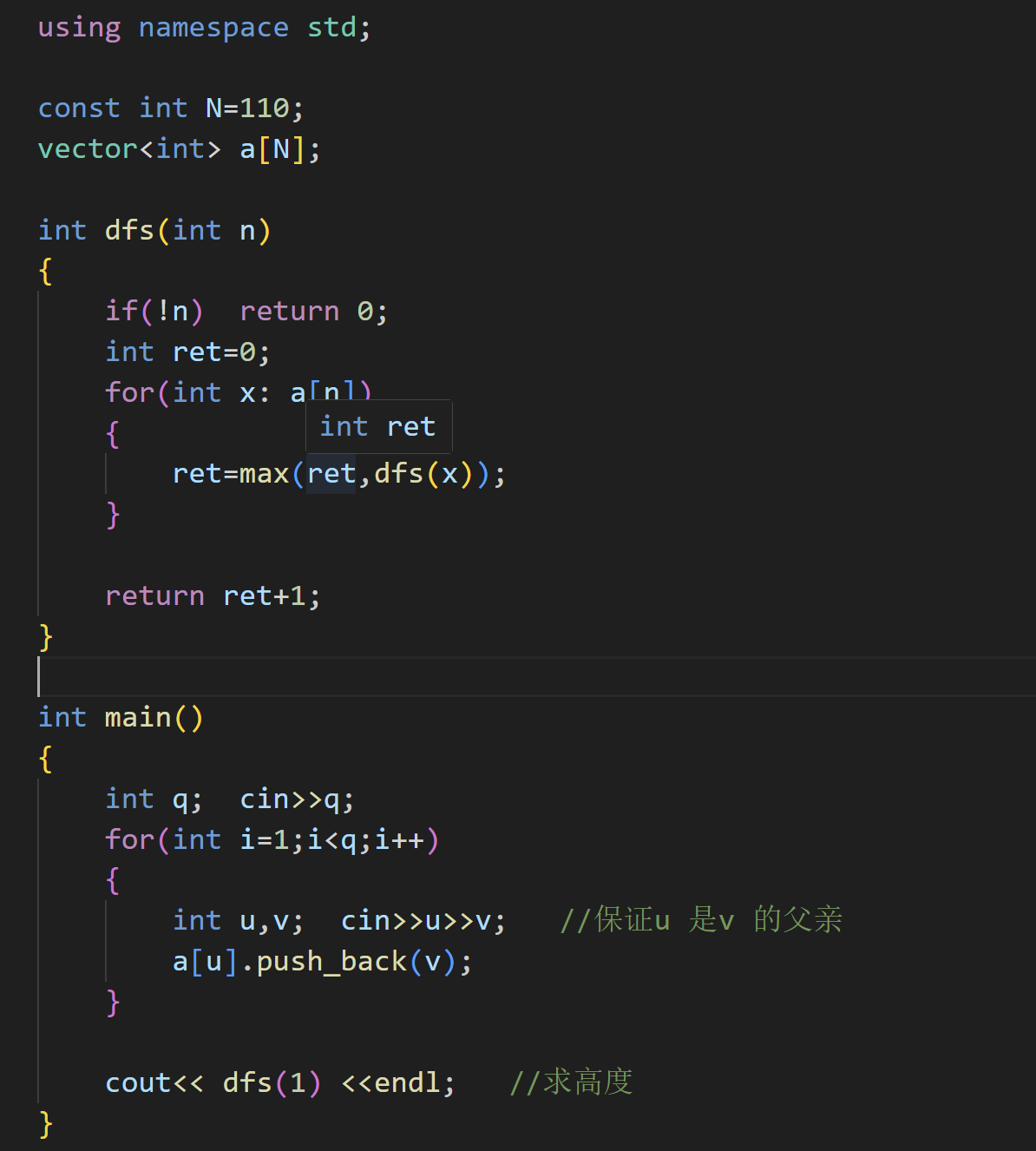
问题2:求宽度
如何求出宽度呢?我们想到进行BFS时,我们是一层一层的遍历二叉树,就可以借助这个思想来求一棵二叉树的最大宽度
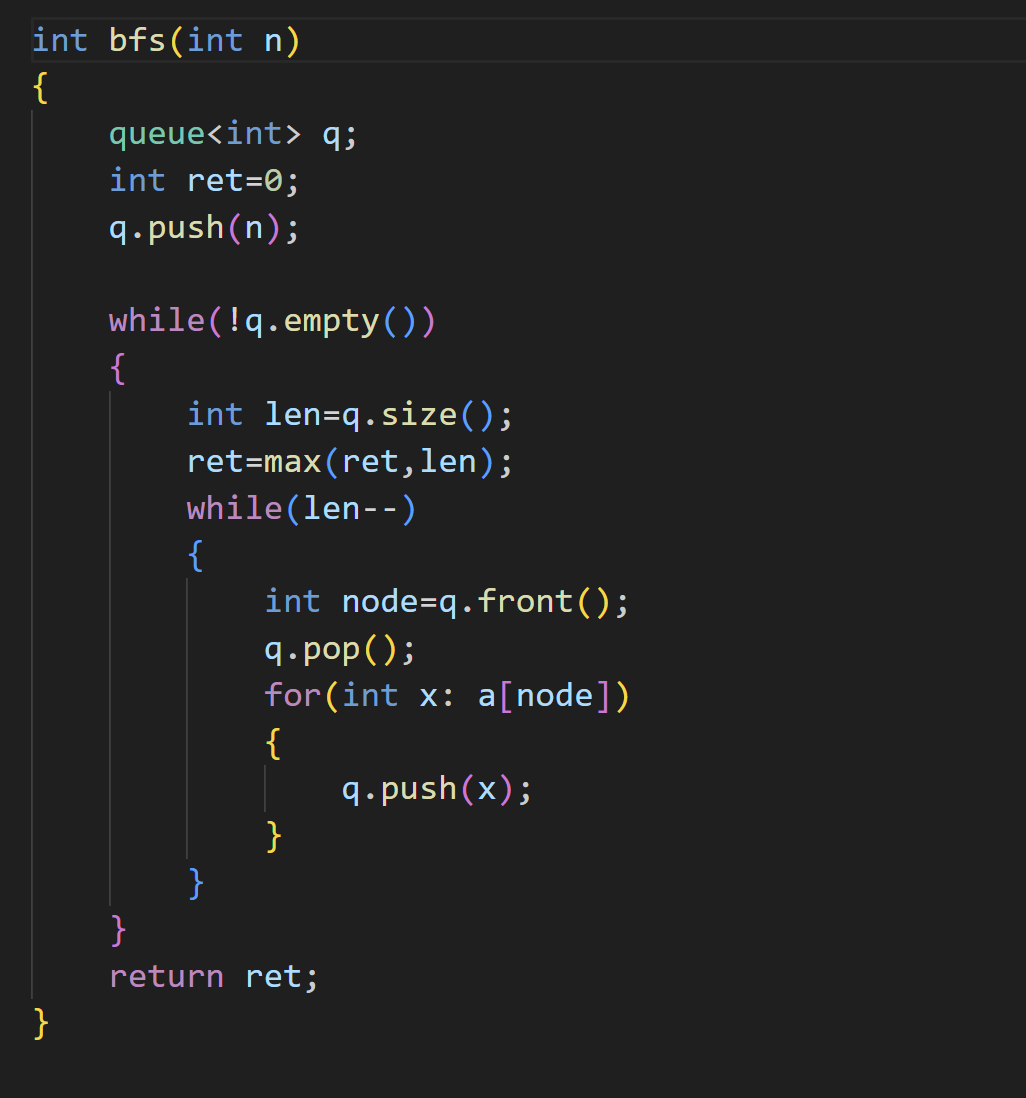
在保证每一层的节点都出队列后,并将它们的孩子入队列,此时更新长度
问题3:距离
首先要搞清楚:向根节点 和 向叶节点 的边数
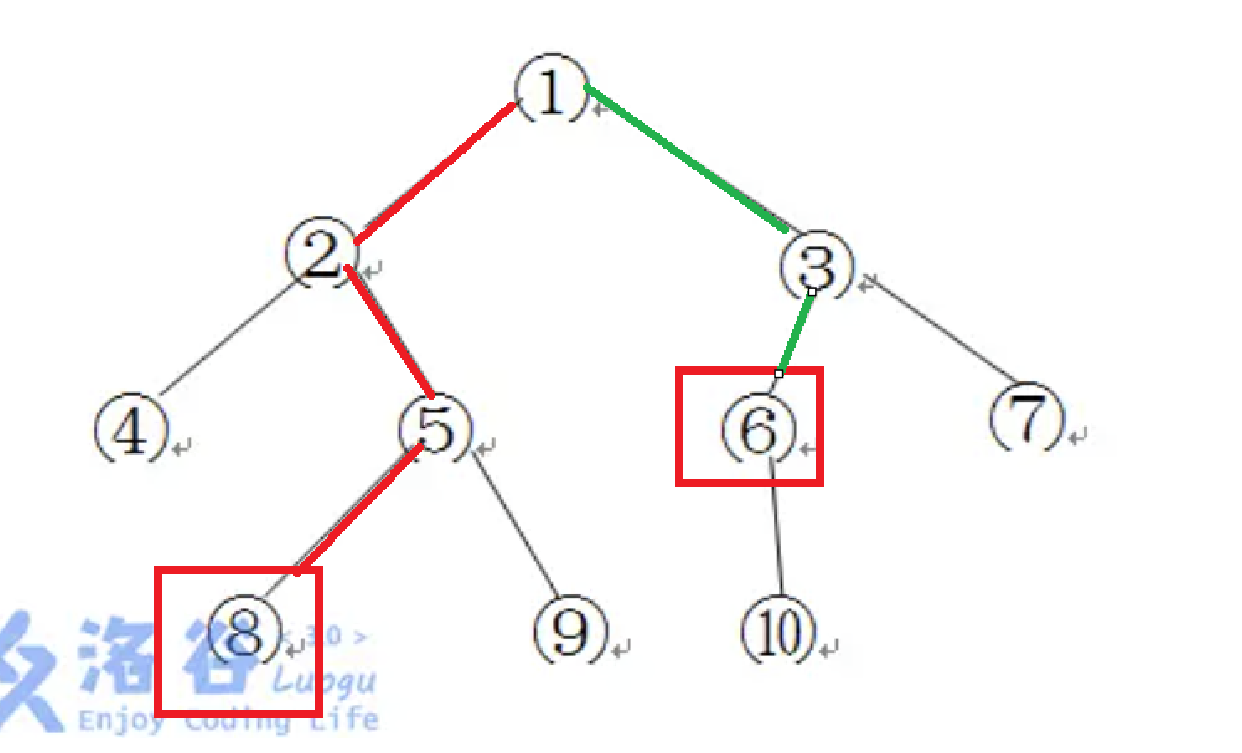
如上图,向上朝向根节点的红色边就是 向根节点的边数,相反,向下朝向叶的绿色边就是 向叶节点的边数,结果就是 3*2+2=8
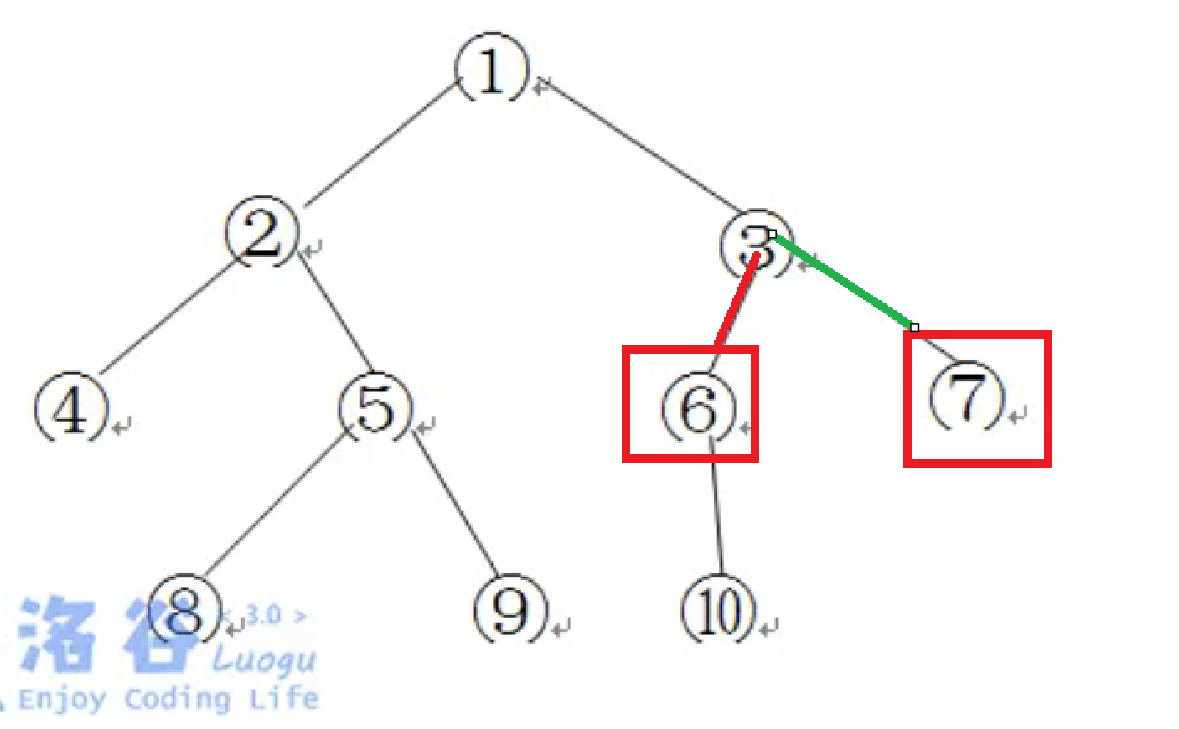
如上图,此时距离为 1*2+1=3
那如何用代码思想呢?
首先我们要计算向根节点的边数,可以从 u 节点开始,一直向上走知道到达根节点,期间记录下每个节点到达 u 节点的距离,定义一个 dis 数组,为了完成向上查找的操作,一开始创建二叉树的时候我们定义一个 fa 数组来记录每一个节点的父亲是谁
要求向叶节点的边数,可以从 v 节点开始,向上遍历,如果过程中有个节点的 dis 对应的值不为 0 ,说明两种边就相遇,可以进行最后计算
完整代码展示:
三.堆
堆之前也是在学习篇中详细的讲解过------>堆
1.实现方式
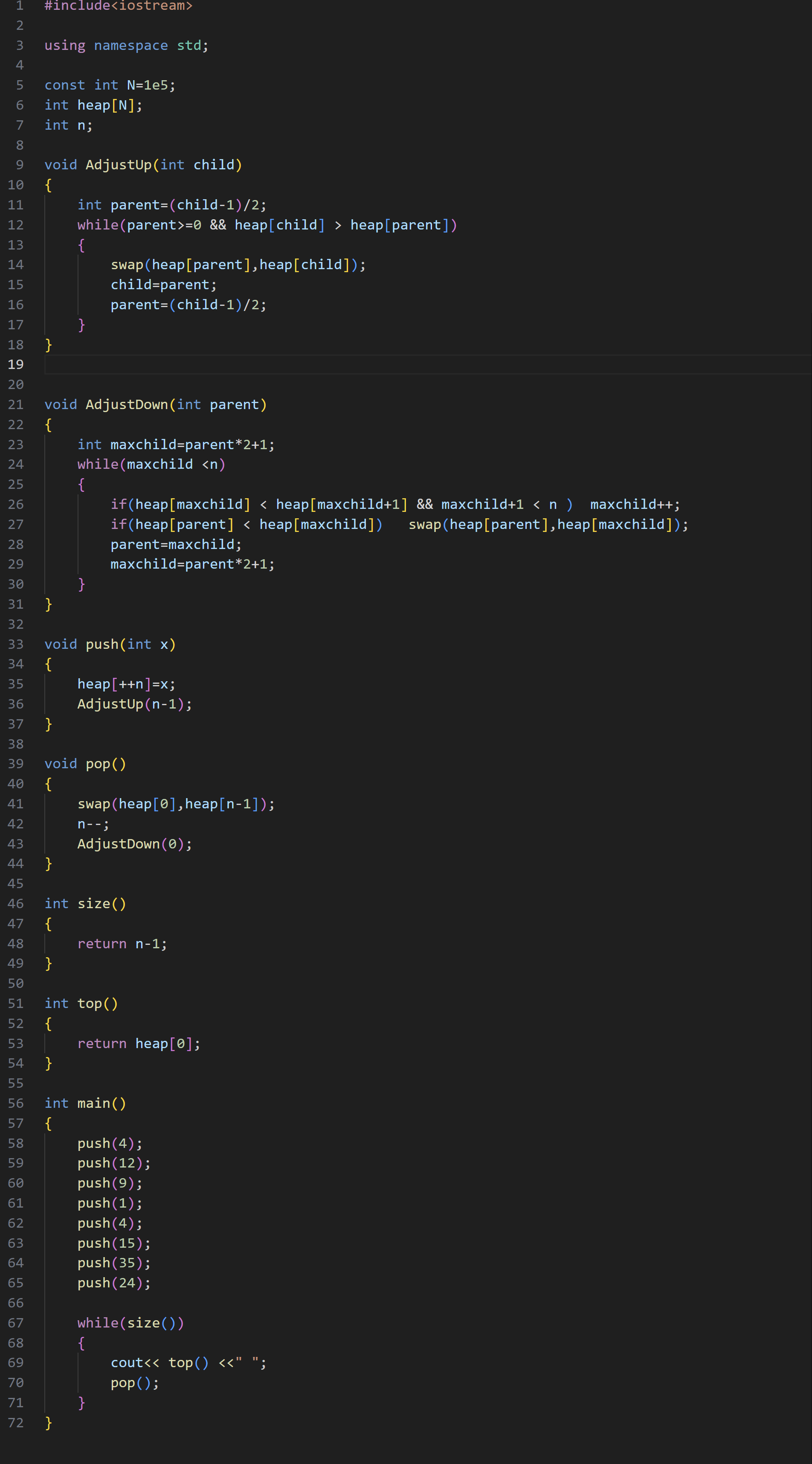
2.STL_priority_queue 优先级队列
普通的队列是⼀种先进先出的数据结构,即元素插⼊在队尾,⽽元素删除在队头。
在优先级队列中,元素被赋予优先级,当插⼊元素时,同样是在队尾,但是会根据优先级进⾏位置调整,优先级越高,调整后的位置越靠近队头;同样的,删除元素也是根据优先级进⾏,优先级最高的元素(队头)最先被删除。
其实可以认为,优先级队列就是堆实现的⼀个数据结构。
priority_queue 就是 C++ 提供的,已经实现好的优先级队列,底层实现就是⼀个堆结构。在算法竞赛中,如果是需要使⽤堆的题⽬,⼀般就直接⽤现成的 priority_queue,很少手写⼀个堆,因为省事
首先就是头文件的包含

定义方式:

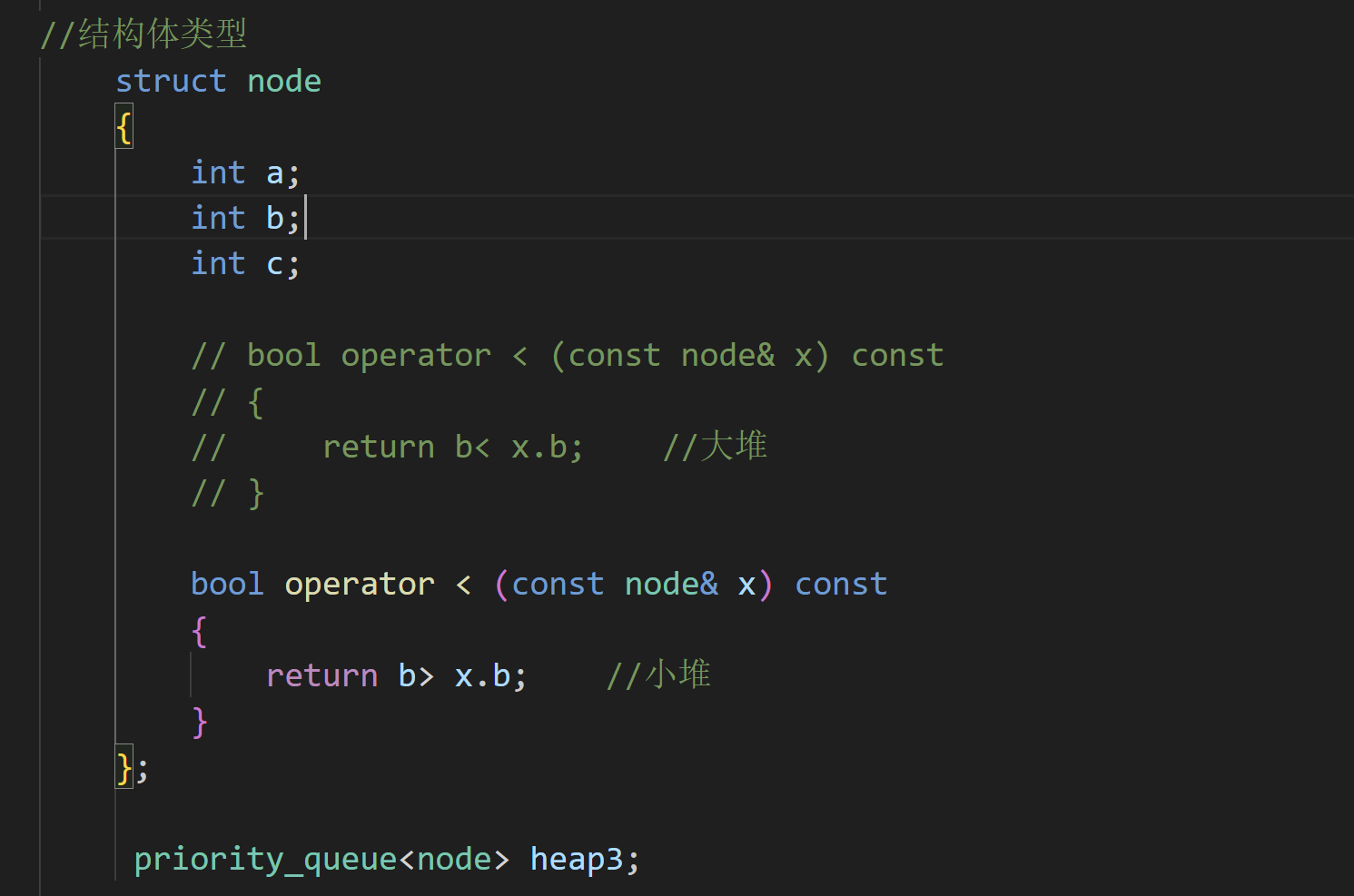
对于内置类型:

对于自定义类型:
要进行运算符重载
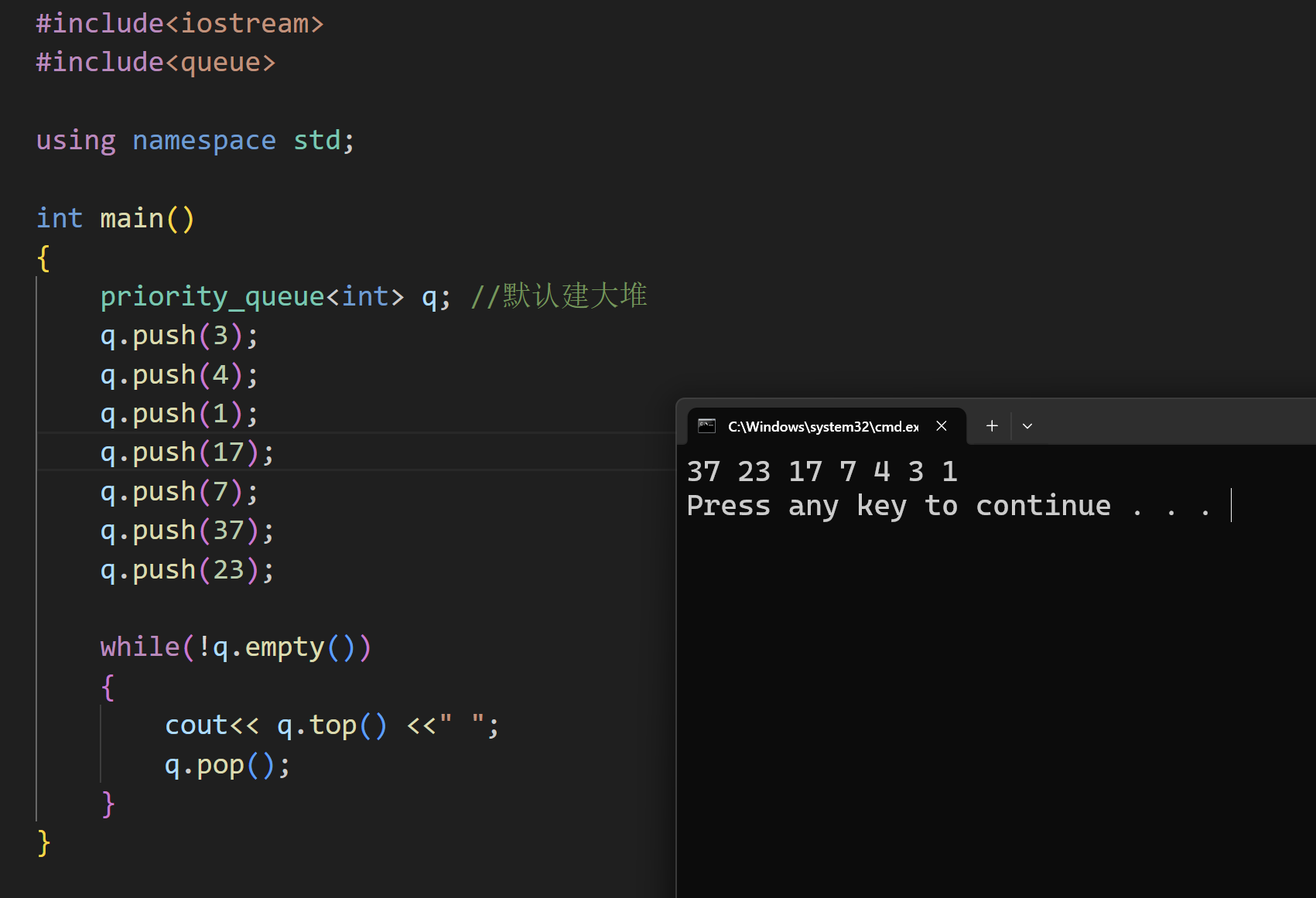
相关函数展示:
3.例题
(1)堆
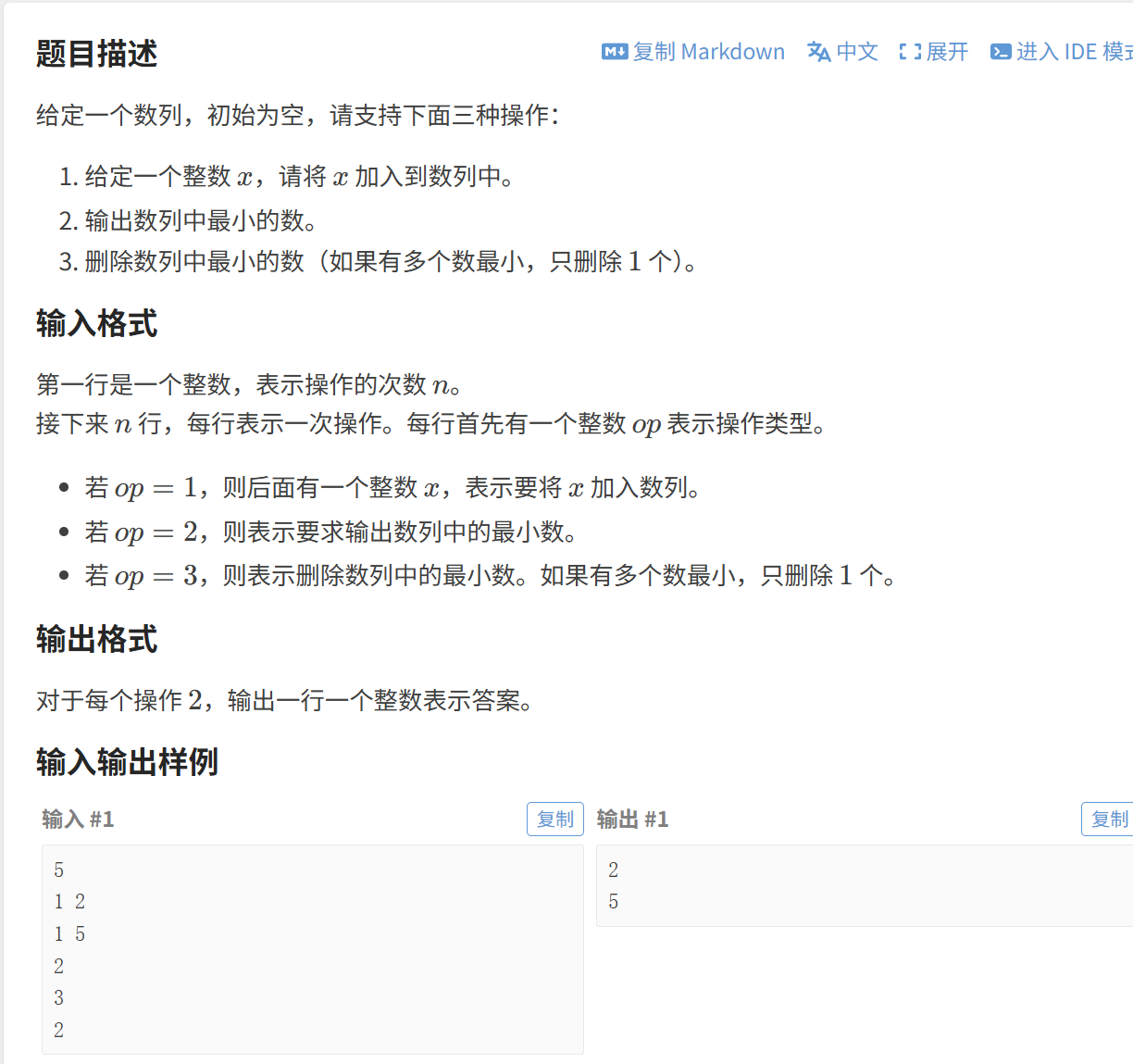
很简单的一道模板题,直接代码展示:
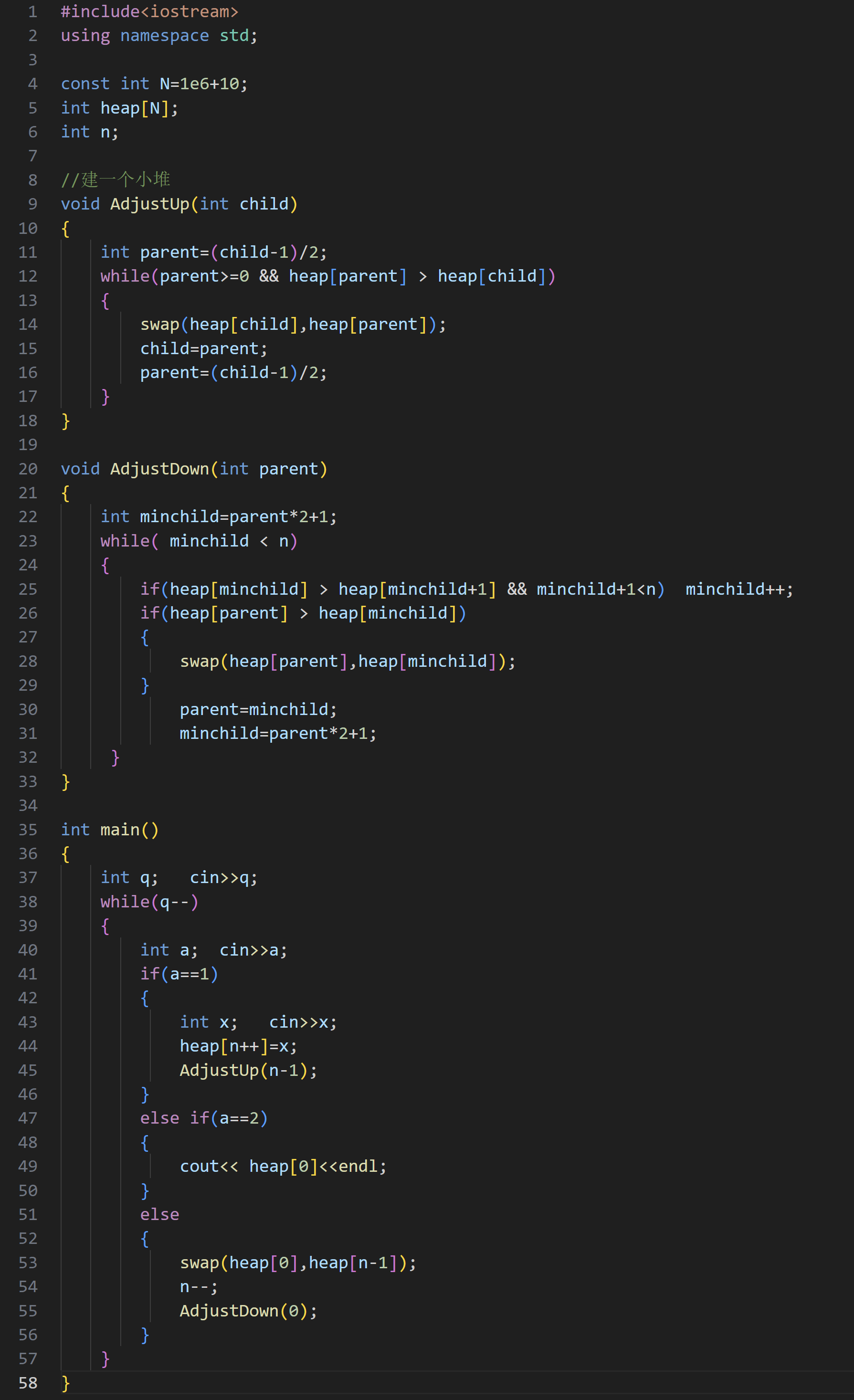
(2)第 k 小

要求第 k 个小的数,就是要建一个大堆,并且保证堆的大小是 k ,要求第 k 小,就每一次返回堆顶的数据(具体解释在学习篇)
代码展示:
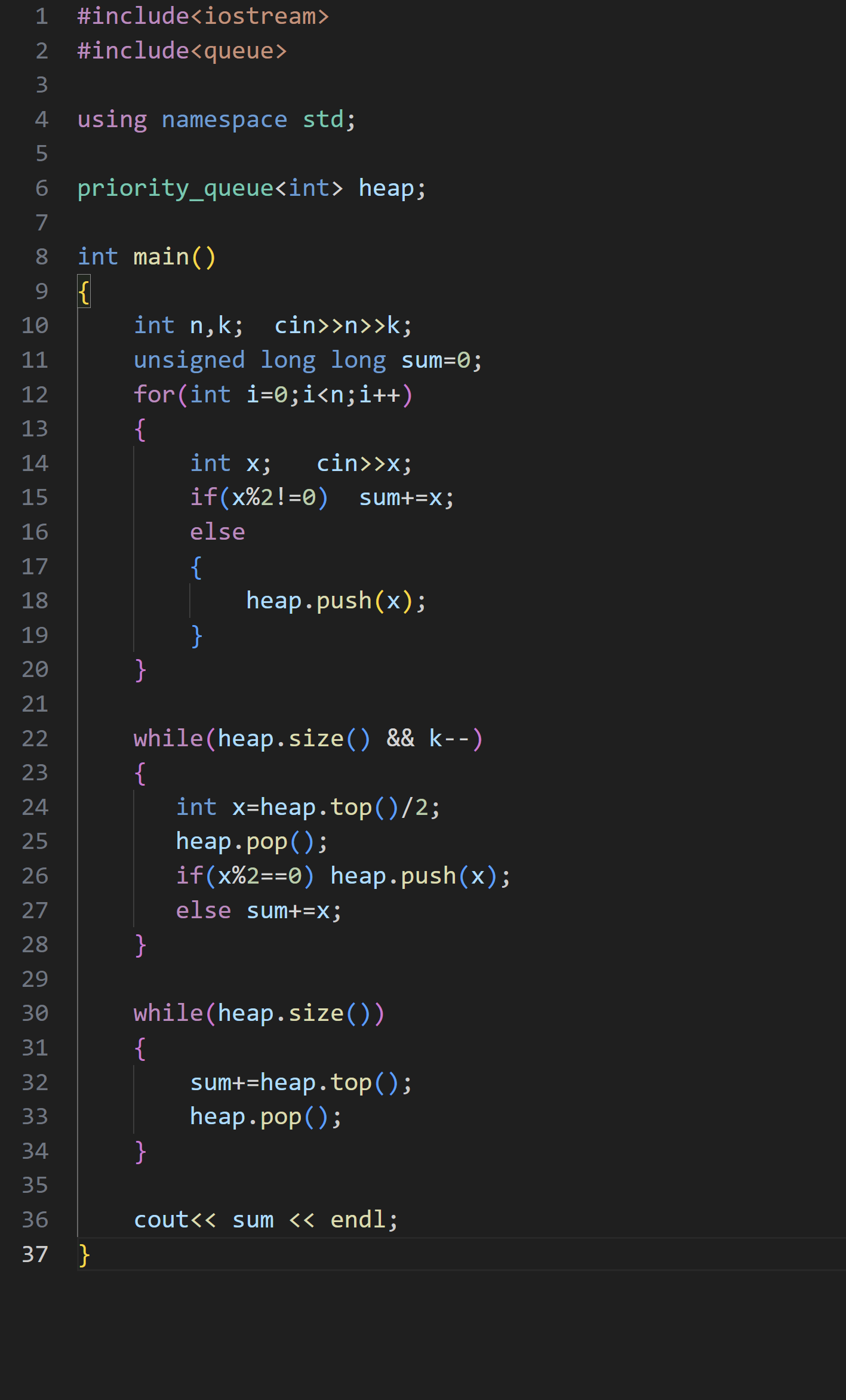
(3)除2
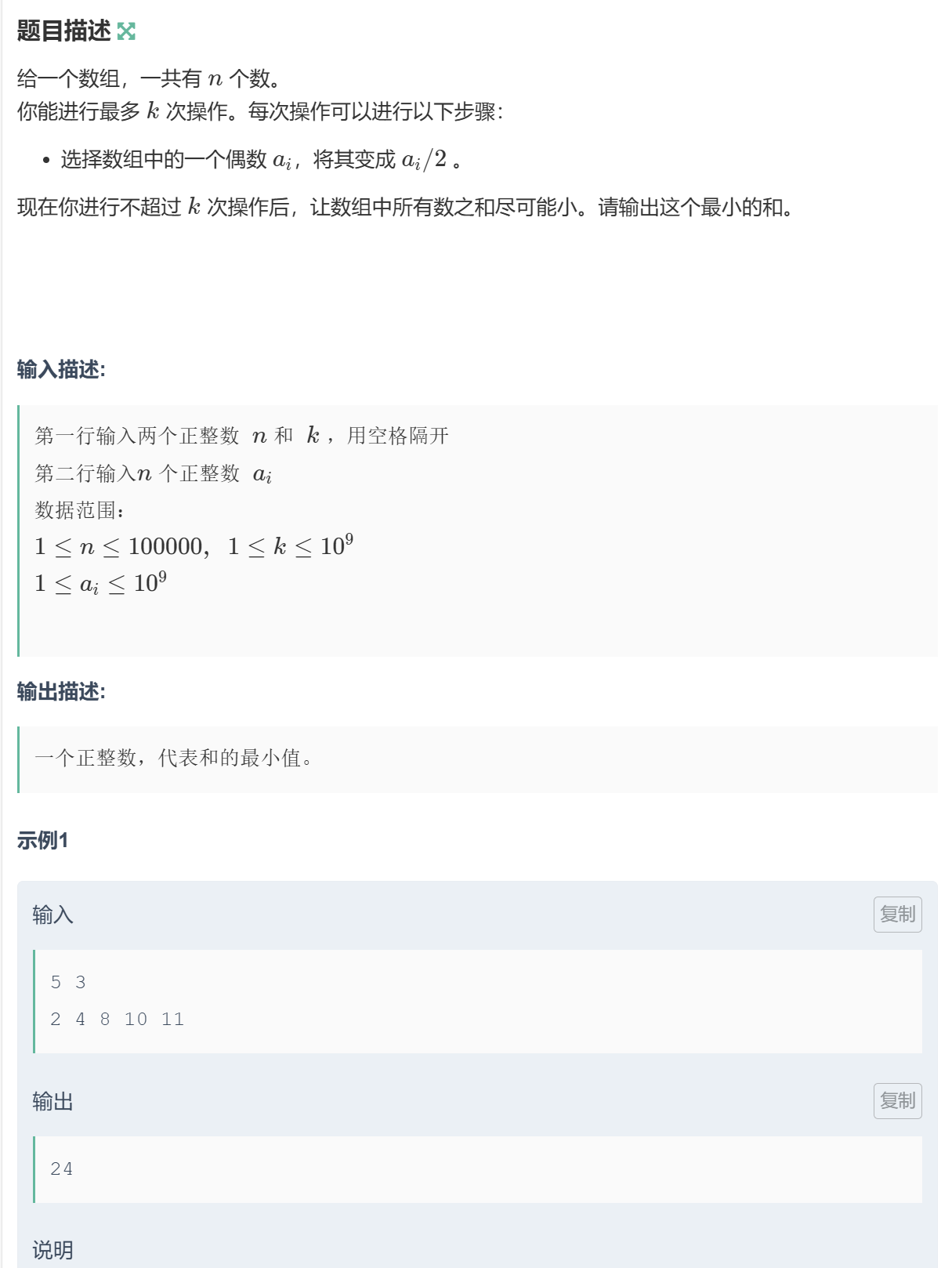
要让最后的和最小,那我们就要在 k 次的范围内每次选最大的偶数,将其除以2
要每次选出最大的偶数,我们就可以建个大堆来实现
可以让偶数全部进堆,奇数加到 sum 中,那么堆顶的数据就是最大的偶数,将其除以2,如果得到的数依然还是偶数,就让这个数重新入堆,如果是奇数,就让其加到 sum 中
当 k 次操作结束后,如果堆里面还有数,就让其全部加到 sum 中
(4)最小函数值
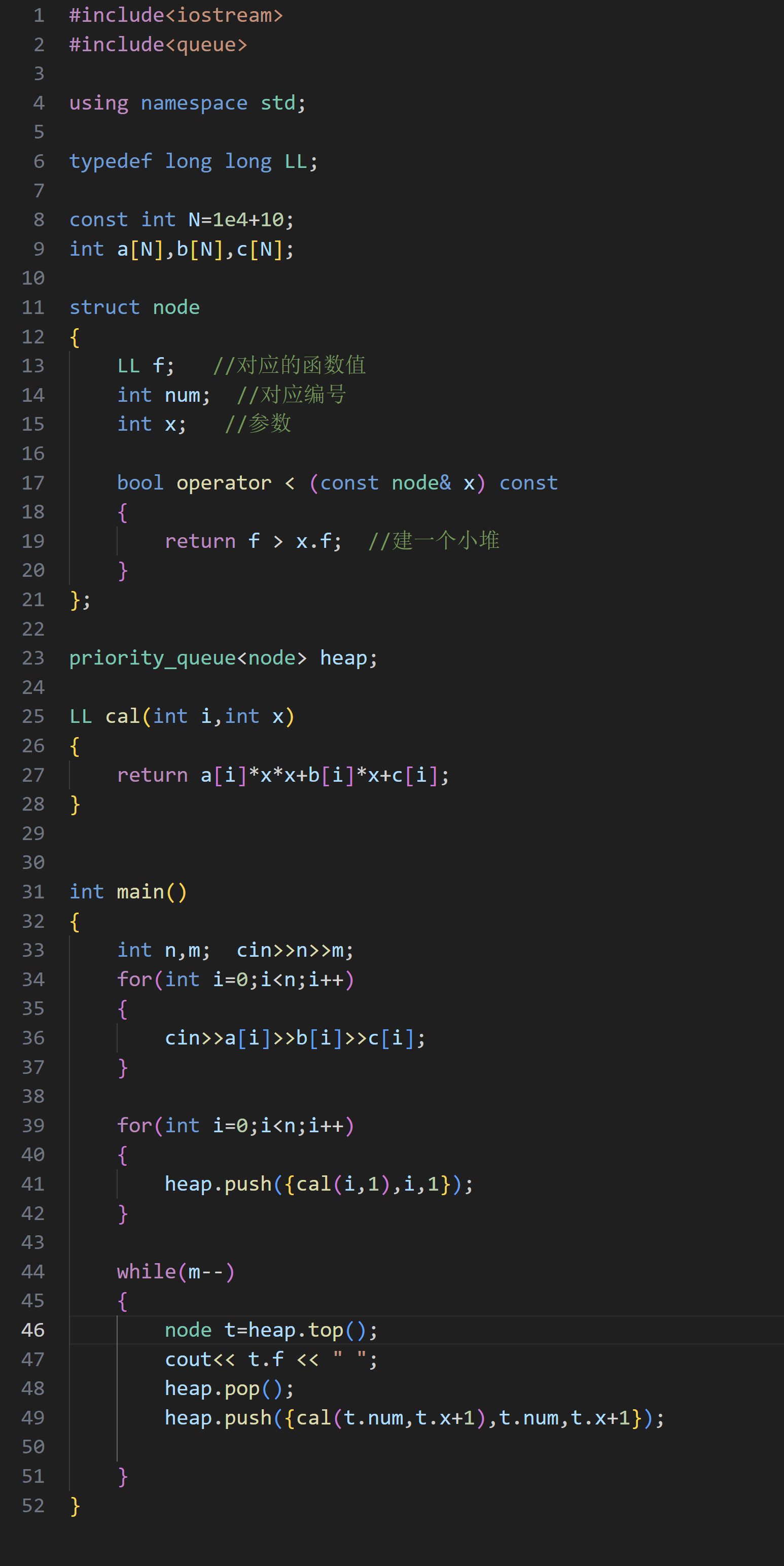
看到题目中要求前几个最小的函数值,就想到可以建个大堆
在堆里面要放进那些值呢?
注意到题目中说,x 值是自然数,对于每一个函数,其就是单调递增的。我们就可以利用这个性质,先让 x==1 时函数值入堆,比较出最小的,然后单独让此自变量 +1 ,继续比较
代码实现:
四.红黑树
1.实现方式
红黑树是一个很复杂的数据结构,我们以后在学习篇具体来拆解学习
我们暂时只要了解:
⼆叉搜索树(也称⼆叉排序树,简称 BST)是⼀颗空树,或者是具有以下特性的⼆叉树;
• 若左⼦树⾮空,则左⼦树上所有结点的值均⼩于根结点的值。
• 若右⼦树⾮空,则右⼦树上所有结点的值均⼤于根结点的值。
• 左、右⼦树也分别是⼀颗⼆叉搜索树。
也就是左⼦树结点值 < 根结点值 < 右⼦树结点值
红黑树当然满足左⼦树结点值 < 根结点值 < 右⼦树结点值,所以中序遍历的结果是递增的
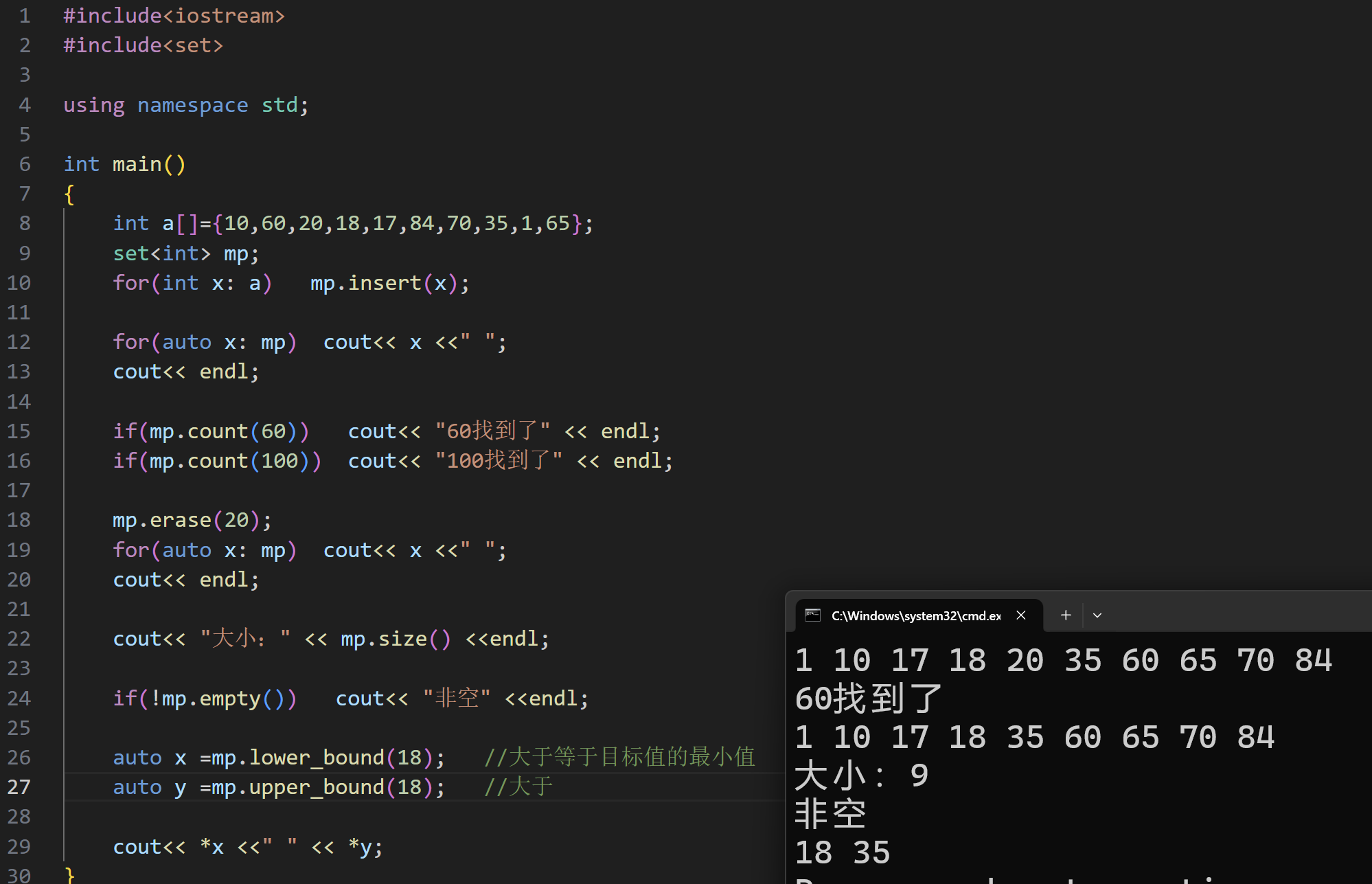
2.STL_set / multiset 和 map / multimap
set / multiset
set 与 multiset 的区别: set 不能存相同元素, multiset 可以存相同的元素,其余的使
用方式基本⼀致。因此,我们有时候可以用set 帮助我们给数据去重。
在这⾥只练习使⽤ set 。 set 会⽤, multiset 也会⽤
首先就是头文件;

异曲同工的初始化:

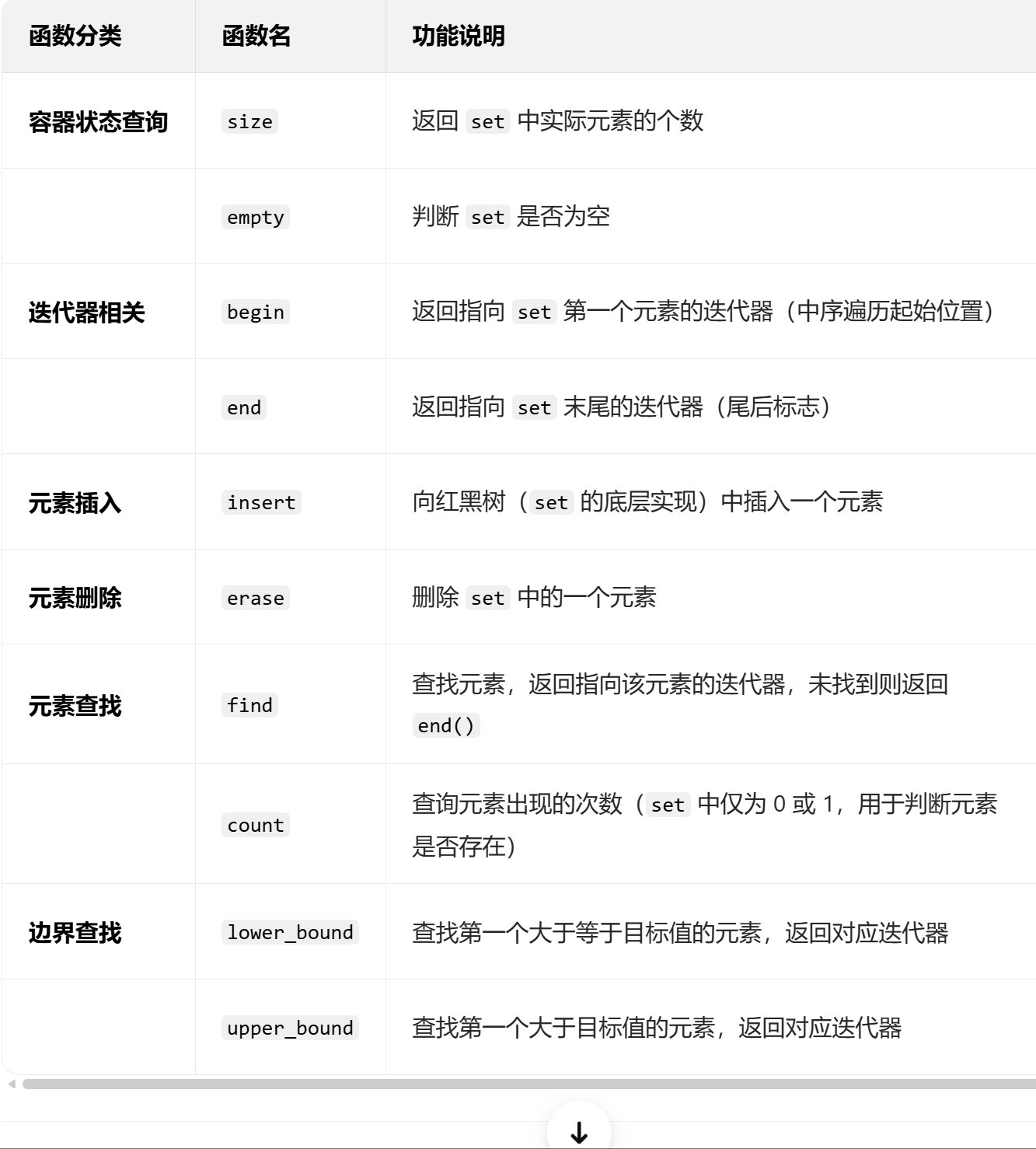
相关函数:
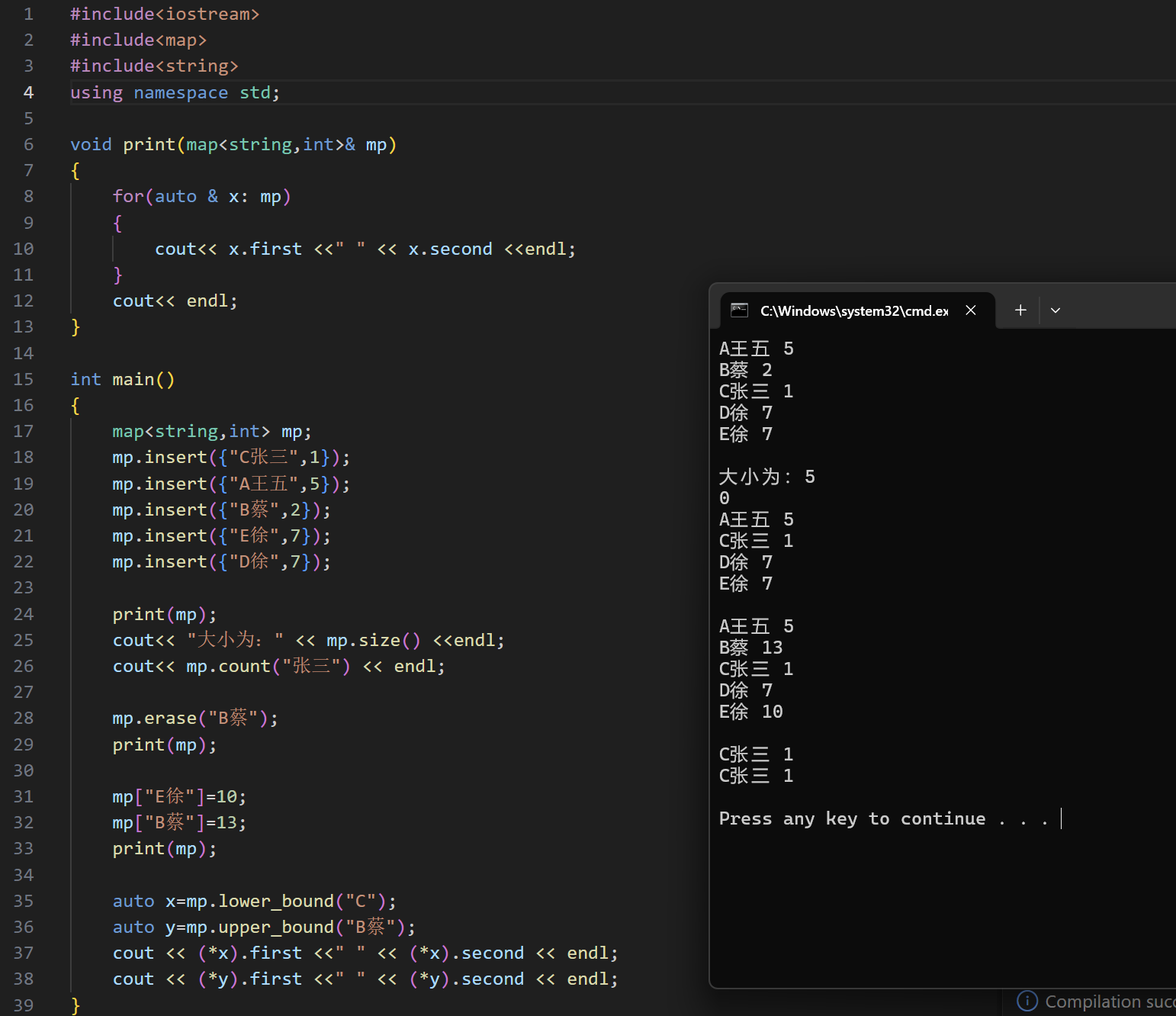
map / multimap
map 与 multimap 的区别: map 不能存相同元素, multimap 可以存相同的元素,其余的使⽤⽅式完全⼀致。因此,这⾥只练习使⽤ map 。
map 与 set 的区别: set 里面存的是⼀个单独的关键字,也就是存⼀个 int 、 char 、
double 或者 string 。而map ⾥⾯存的是⼀个 pair<key, value> ,(k-v 模型)不仅
有⼀个关键字,还会有⼀个与关键字绑定的值,比较方式是按照 key 的值来比较。
可以这样理解:红黑树里面⼀个⼀个的结点都是⼀个结构体,里面有两个元素分别是 key 和value 。插⼊、删除和查找的过程中,比较的是 key 的值。
比如,我们可以在 map 中:
• 存 <int, int> ,来统计数字出现的次数;
• 存 <string, int> ,来统计字符串出现的次数;
头文件:

初始化:

相关函数:

3.例题
(1)英语作文
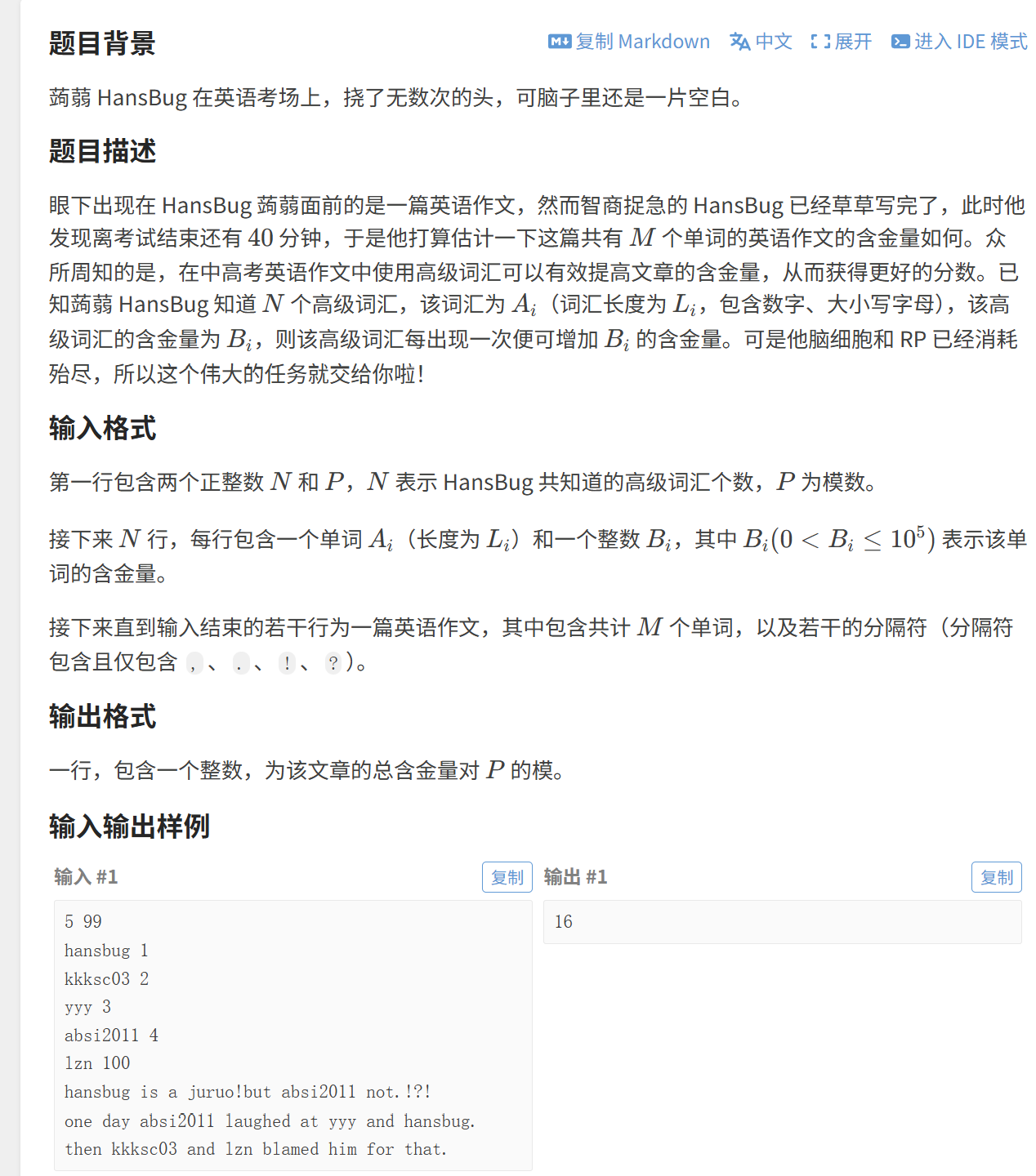
每一个 "单词" 就对应着一个数字,这里我们就可以用 map< string,int > 这个数据结构
因为短文中含有空白字符、数字、符号,读取的时候我们可以一个字符一个字符的读取
代码展示:
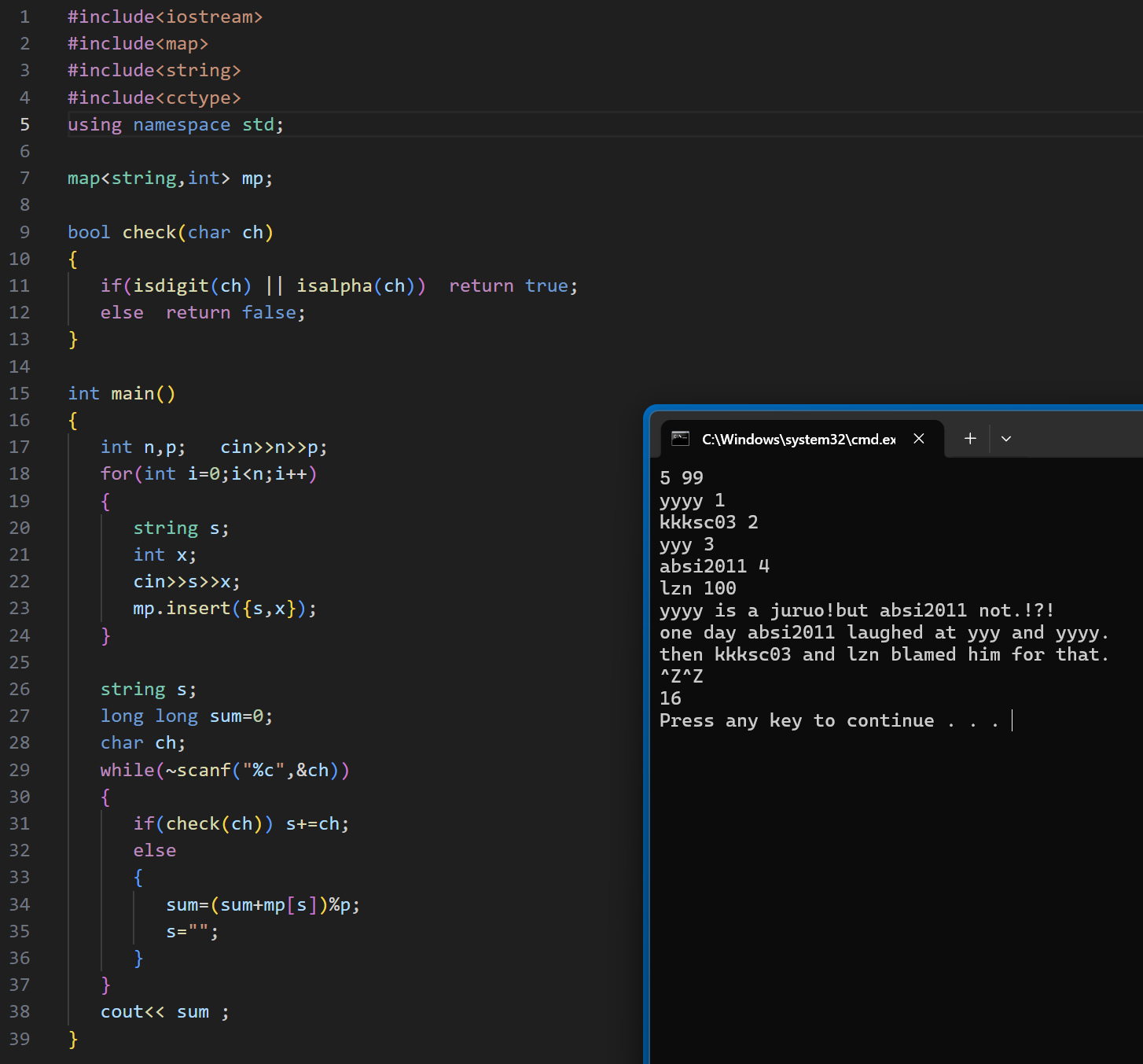
(注意这里使用 scanf,因为其可以自动跳过空白字符)
(2)营业额统计
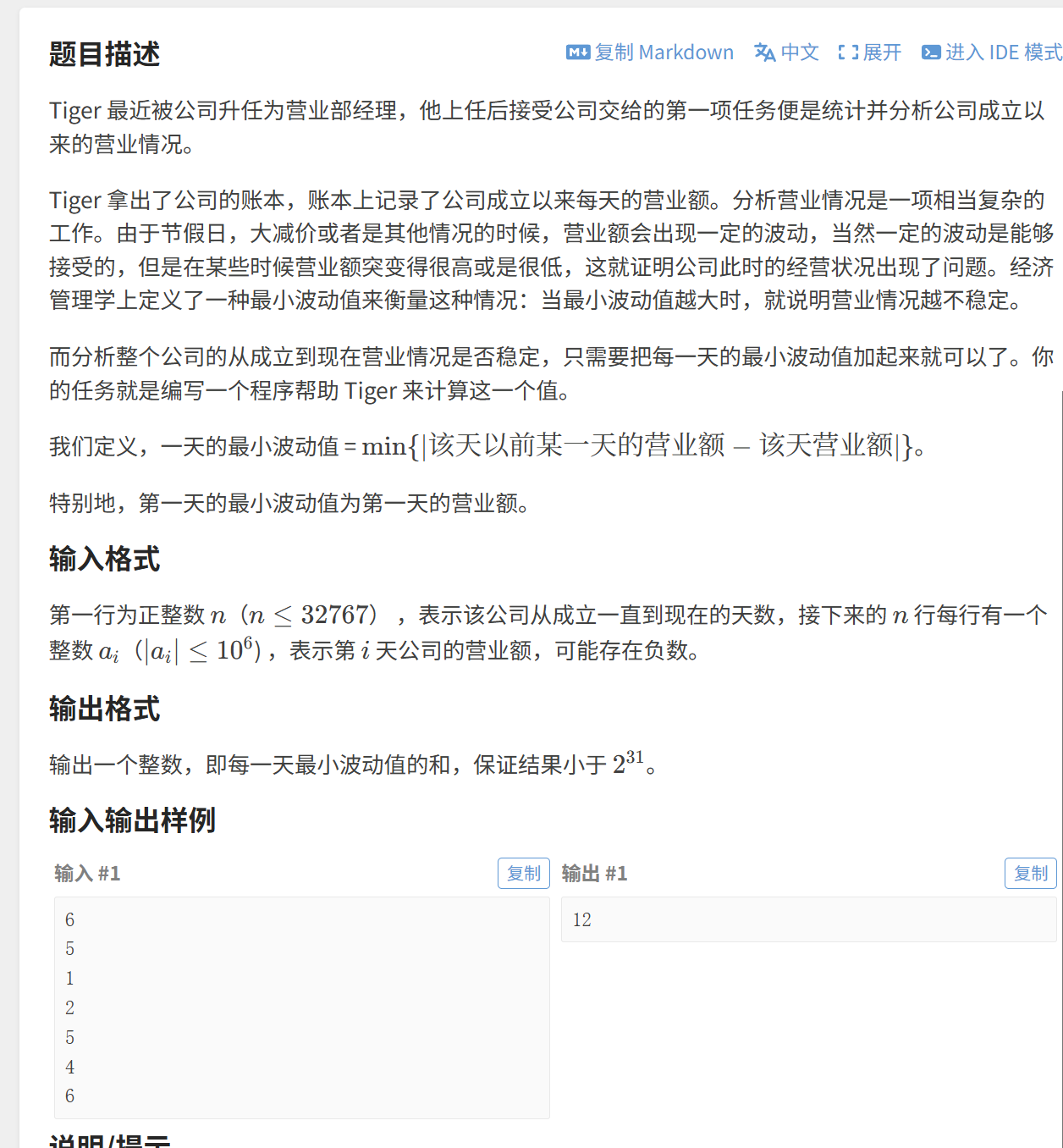
这道题简单来说就是,遍历到某一个数时,去这个数的前面去找一个离其最近的数,累加最小差值,也就是说我们要去找离目标数最近的一个数
还记得 lower_bound(x) 函数吗,他可以查询到大于等于 x 的一个数,返回迭代器 it,那么 it-1 就是离 x 最近的并小于它的数,我们只需要比较这两个数谁离 x 更近就行
代码展示:
五.哈希表
哈希表(hash table),⼜称散列表,是根据关键字可以直接访问数据的数据结构。
哈希表建⽴了⼀种关键字和存储地址之间的直接映射关系,使每个关键字与结构中的唯⼀存储位置相对应。理想情况下,在哈希表中进行查找的时间复杂度为 O(1) ,即与表中的元素数量无关。因此哈希表是⼀种存储和查找非常快的结构。
哈希函数
将关键字映射成对应的地址的函数就是哈希函数,也叫作散列函数
记为 Hash(key) = Addr 。
哈希函数的本质也是⼀个函数,它的作⽤是,你给它⼀个关键字,它给你⼀个该关键字对应的存储位置。
简单来说,哈希函数就是计算数据是如何进行映射的一个操作
常见的哈希函数:
(1)直接定址法
直接取关键字的某个线性函数值为散列地址,散列函数是 hash(key) = key 或 hash(key)= a× key + b
其中 a 与 b 为常数。这种⽅式计算⽐较简单,适合关键字的分布基本连续的情况,但是若关键字分布不连续,空位较多,则会造成存储空间的浪费。
例如,我们常常把字符的 ASCLL 表的数直接作为数组的下标
(2)除留余数法
除留余数法,顾名思义,假设哈希表的⼤⼩为 M,那么通过 key 除以 M 的余数作为映射位置的下标,
也就是哈希函数为:hash(key) = key % M。因此,这种⽅法的重点就是选好模数 M。
• 建议 M 取不太接近 2 的整数次冥的⼀个质数(素数)
哈希冲突
哈希函数可能会把两个或两个以上的不同关键字映射到同⼀地址,这种情况称为哈希冲突,也称散列冲突。起冲突的不同关键字,称它们为同义词。
例如,用除留余数法,就存在两个数除以 M 的余数是同一个数,将会存放在同一个位置,这就有了哈希冲突
解决哈希冲突
(1)线性探测法
如果一个数要存放的位置发生了哈希冲突,就让其往后移动,直到遇到空位为止(到尾了就从头开始)
(2)链地址法
所有的数据不再直接存储在哈希表中,哈希表中存储⼀个指针,没有数据映射这个位置时,这个指针为空,有多个数据映射到这个位置时,我们把这些冲突的数据链接成⼀个链表,挂在哈希表这个位置下⾯。
和树链式前向星是一样的
1.实现方式
(1)线性探测
初始化
和其他的数据结构不同,哈希表的模拟实现中,我们要进行初始化,数组中一开始放的是不可能存放的值,表示是空位

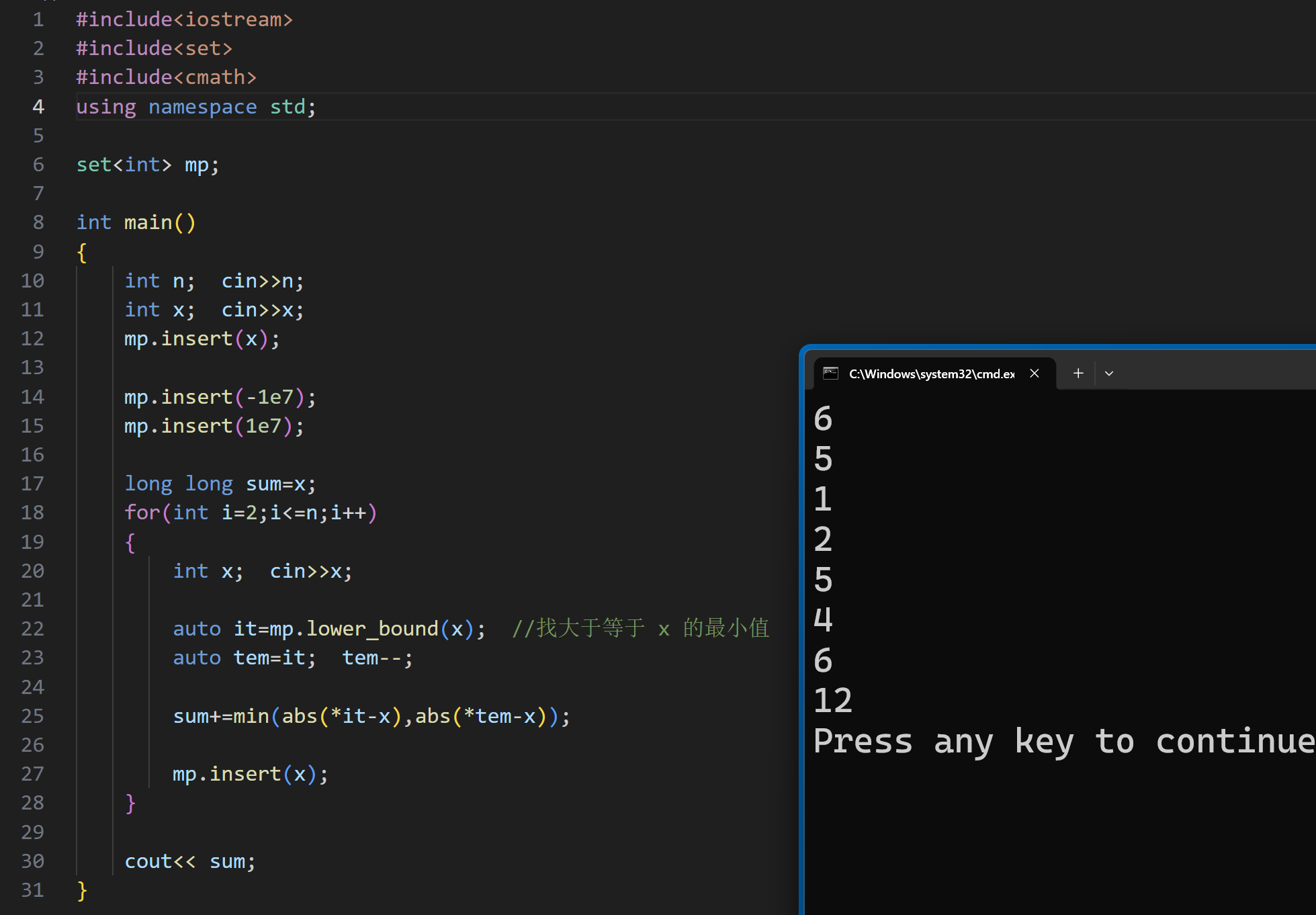
下标计算函数
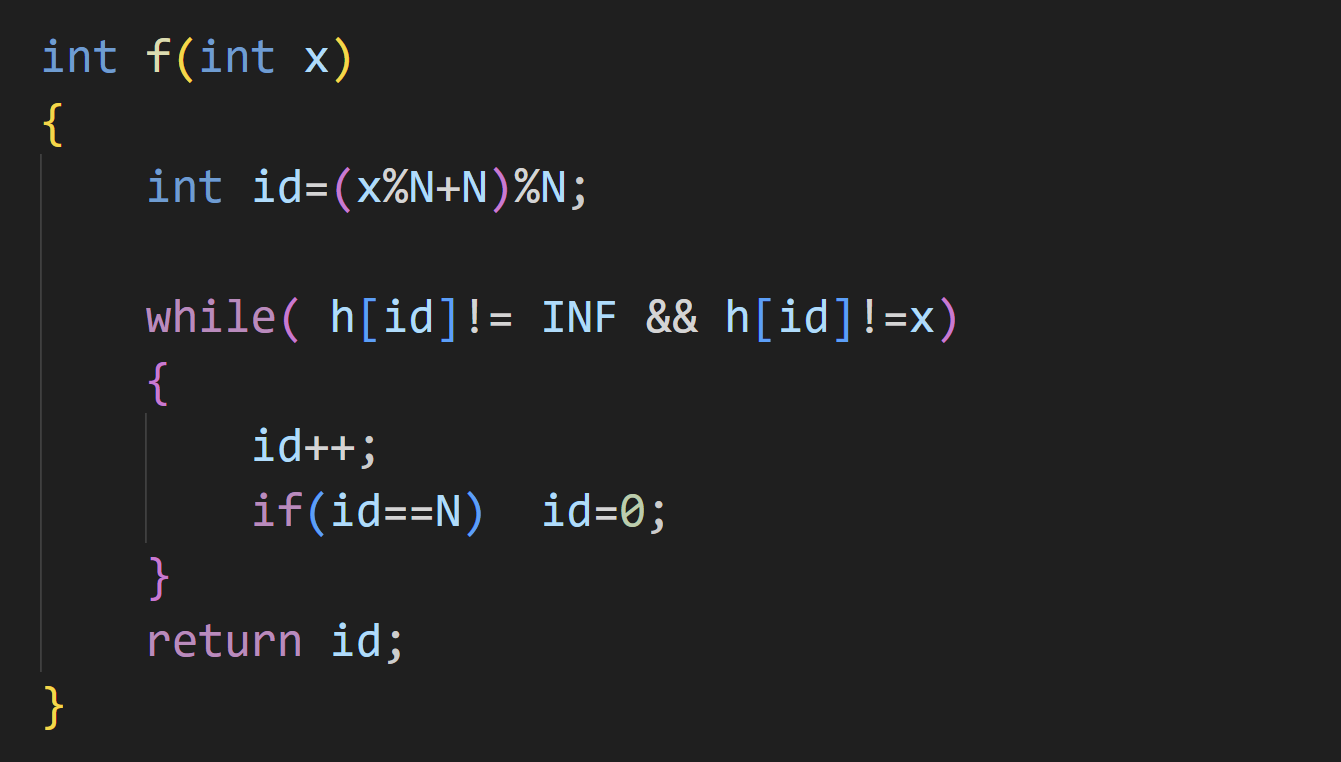
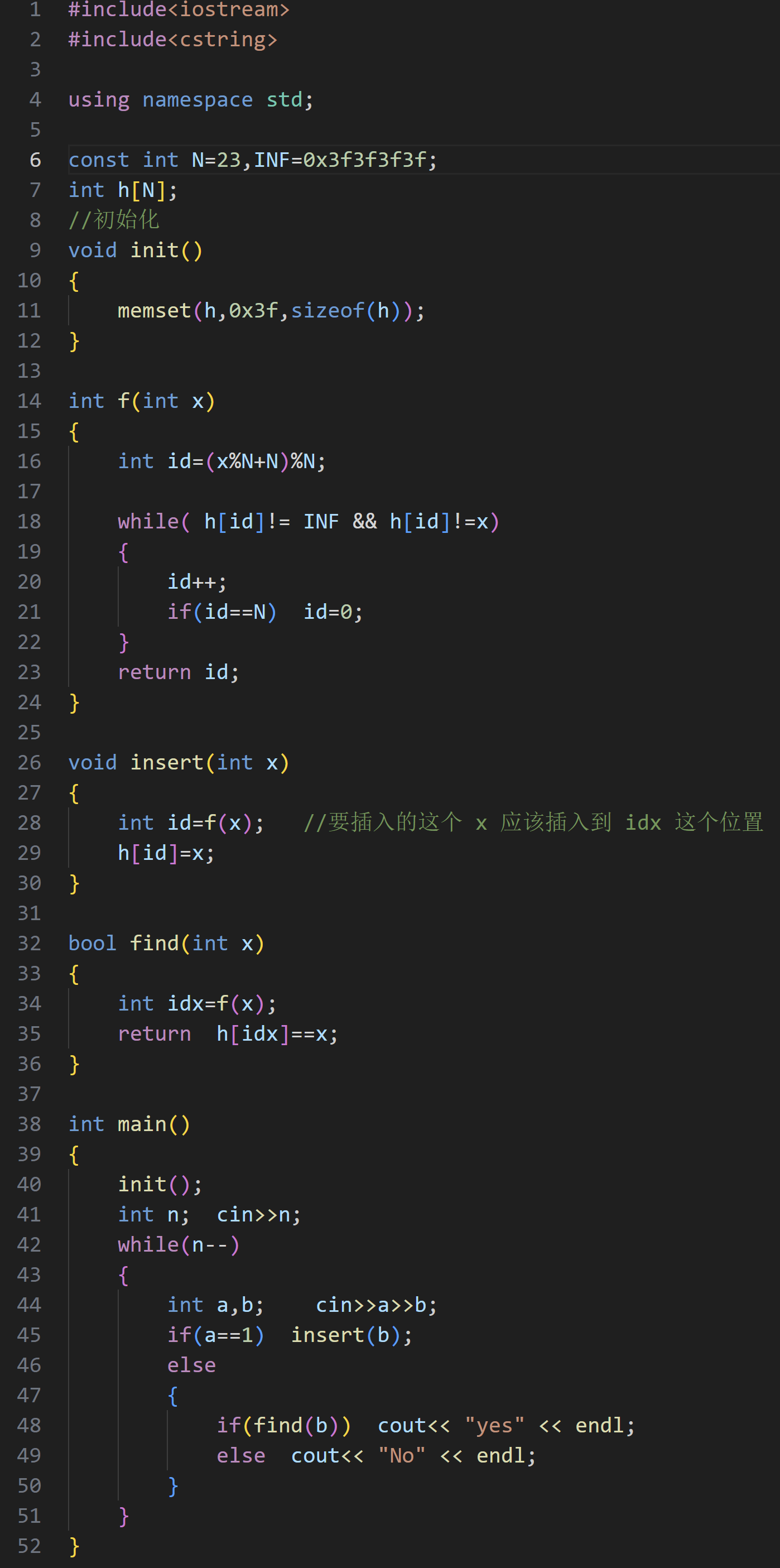
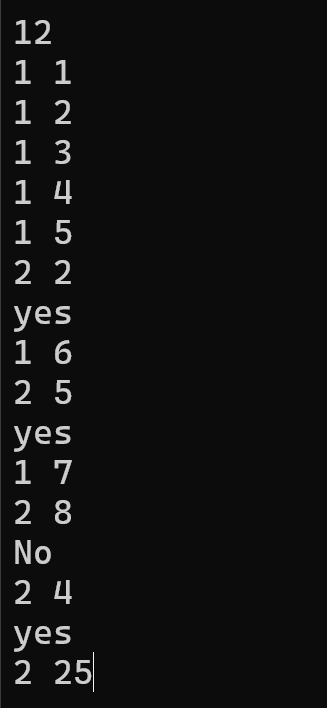
(2)链地址法
2.STL_ unordered_set / unordered_multiset 和 unordered_map / unordered_multimap_
unordered_set / unordered_multiset
set 与 unordered_set 的区别就是:
前者是⽤红⿊树实现的,后者是⽤哈希表实现的
使⽤的⽅式是完全⼀样的。⽆⾮就是存储和查找的效率不⼀样,以及前者存的是有序的,后者⽆序
头文件;

初始化:

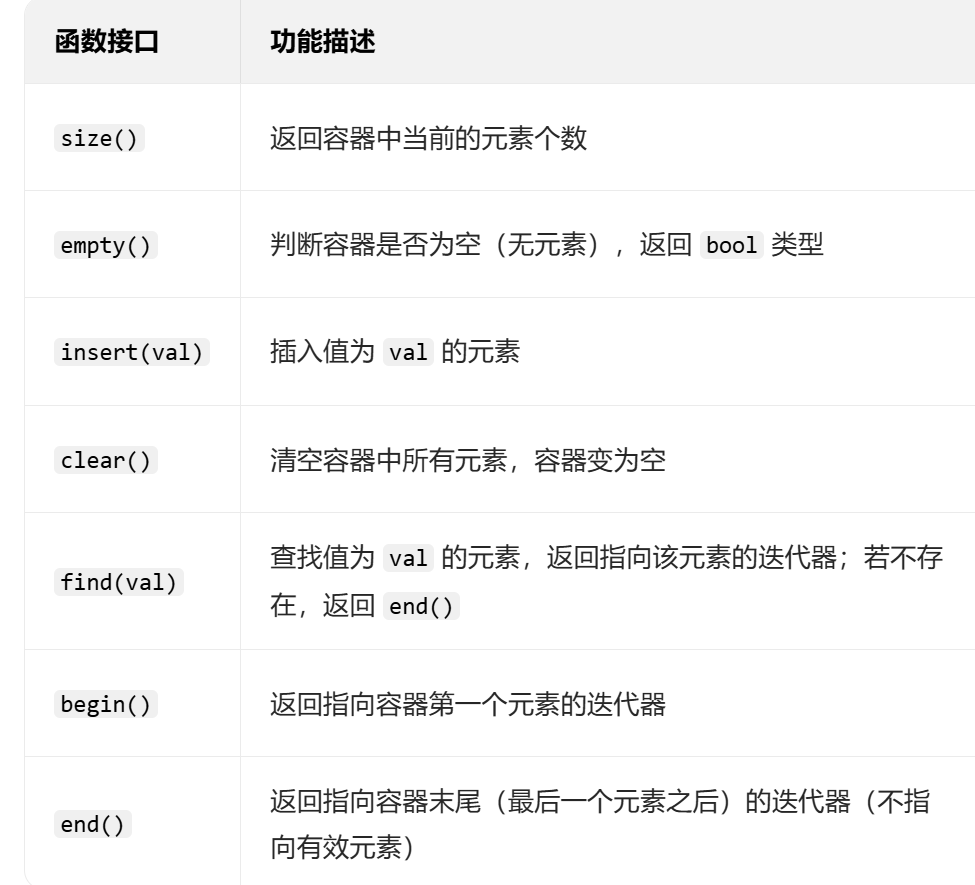
相关函数:
unordered_map / unordered_multi
头文件:

初始化:

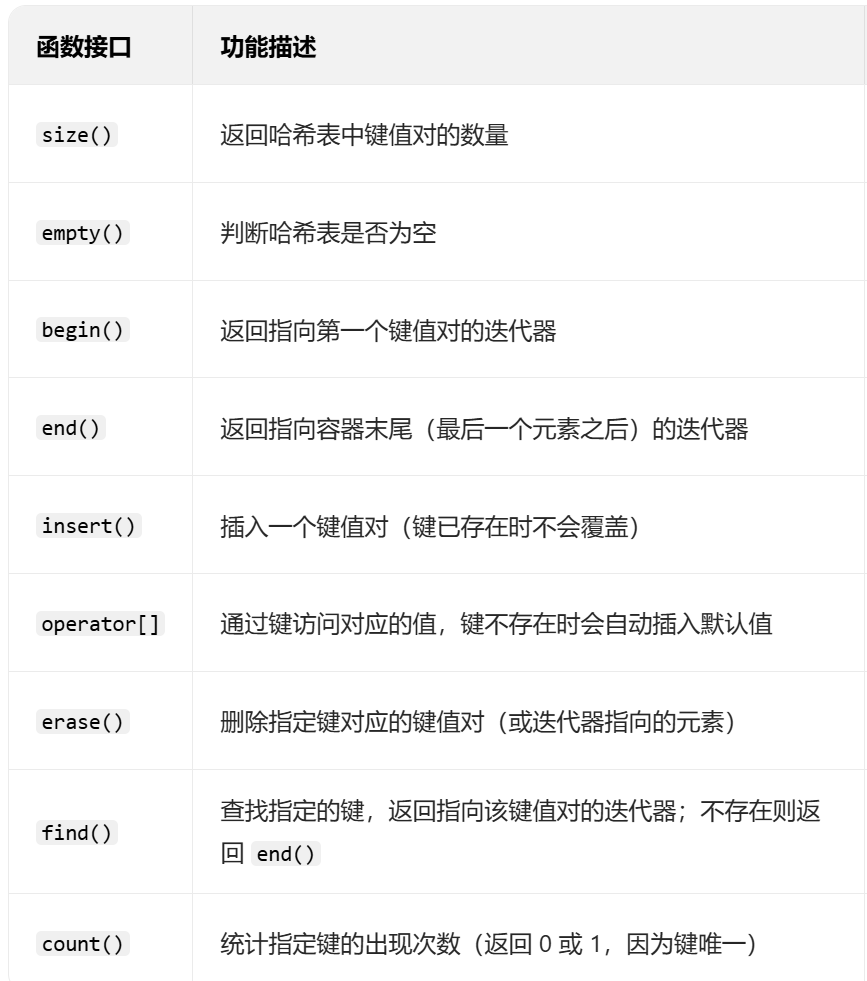
相关函数:
3.例题
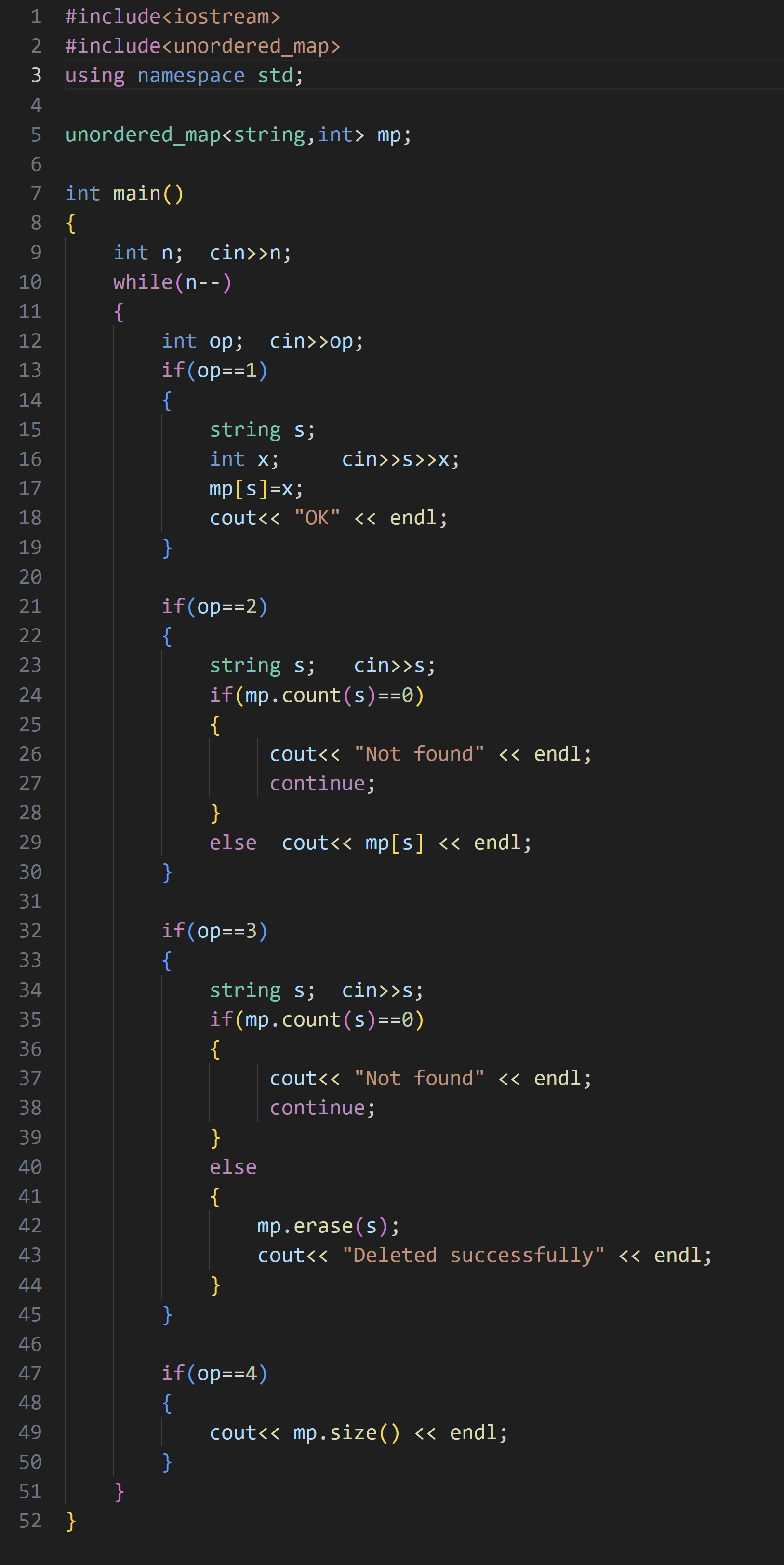
(1)学籍管理

模板题,直接代码展示:
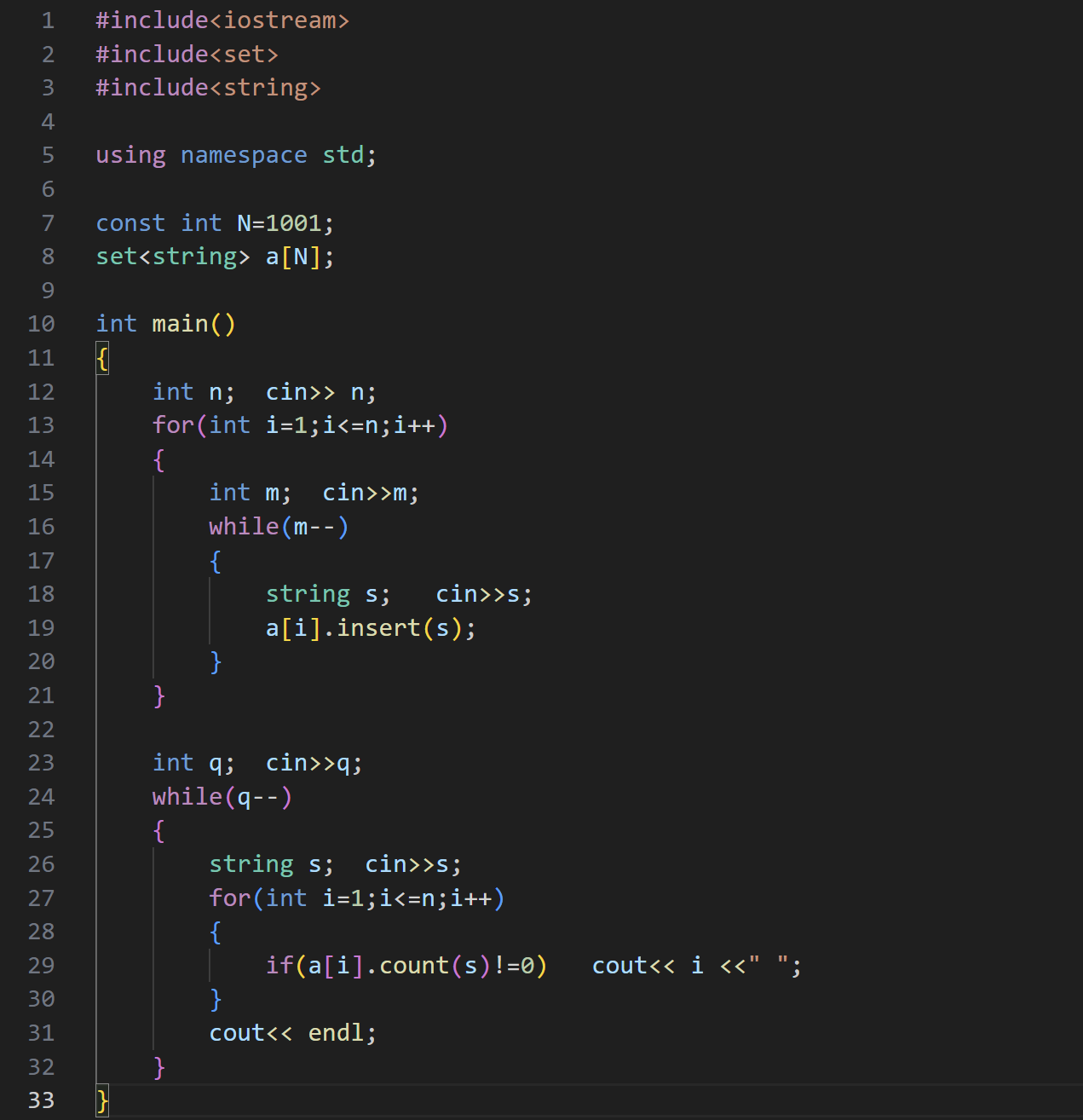
(2)阅读理解

我们可以创建一个哈希数组,将每一篇中每一个单词都放到哈希表中,询问时,如果这个单词存在于哈希表中,返回数组标号
(3)城市和州
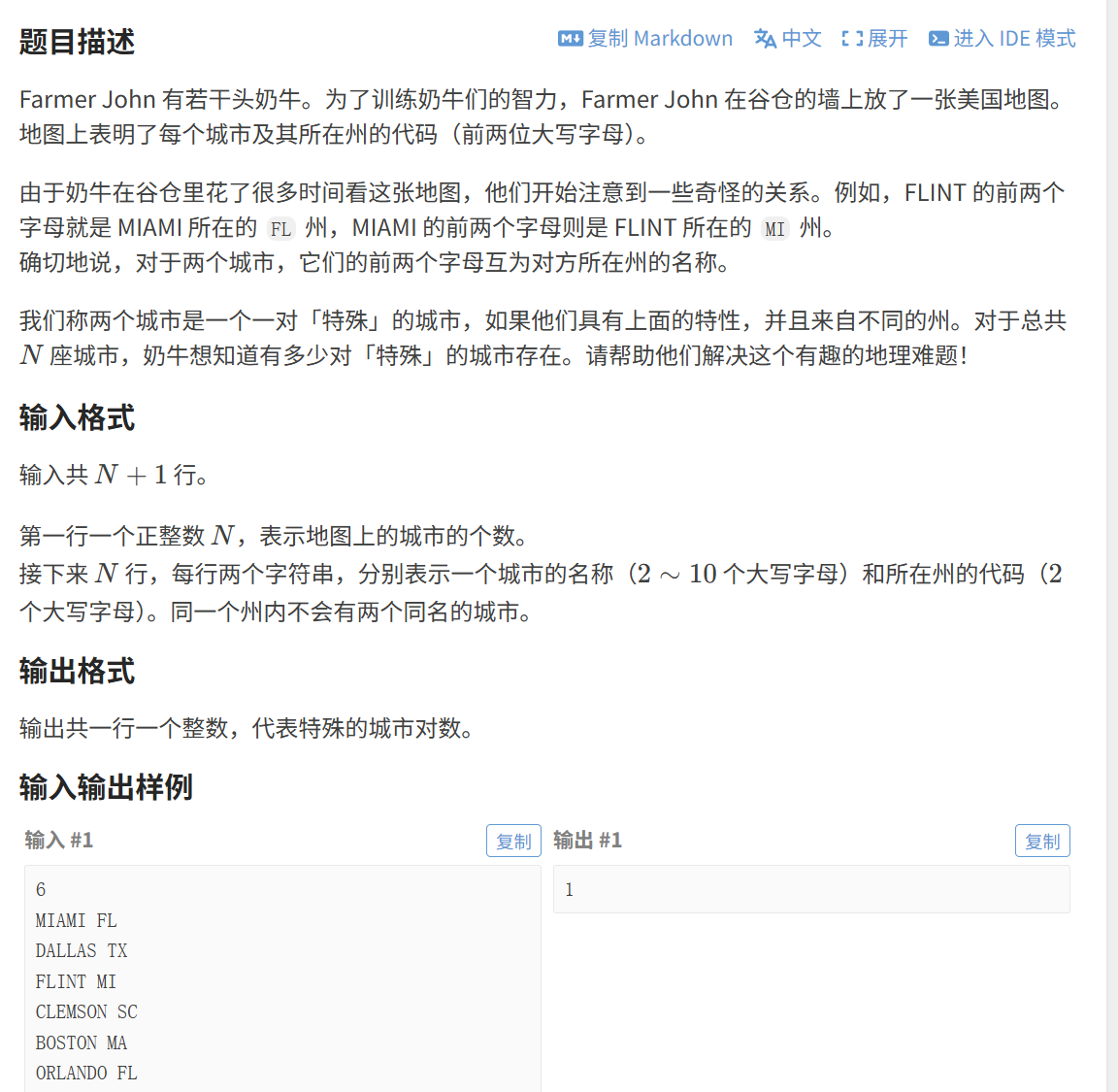
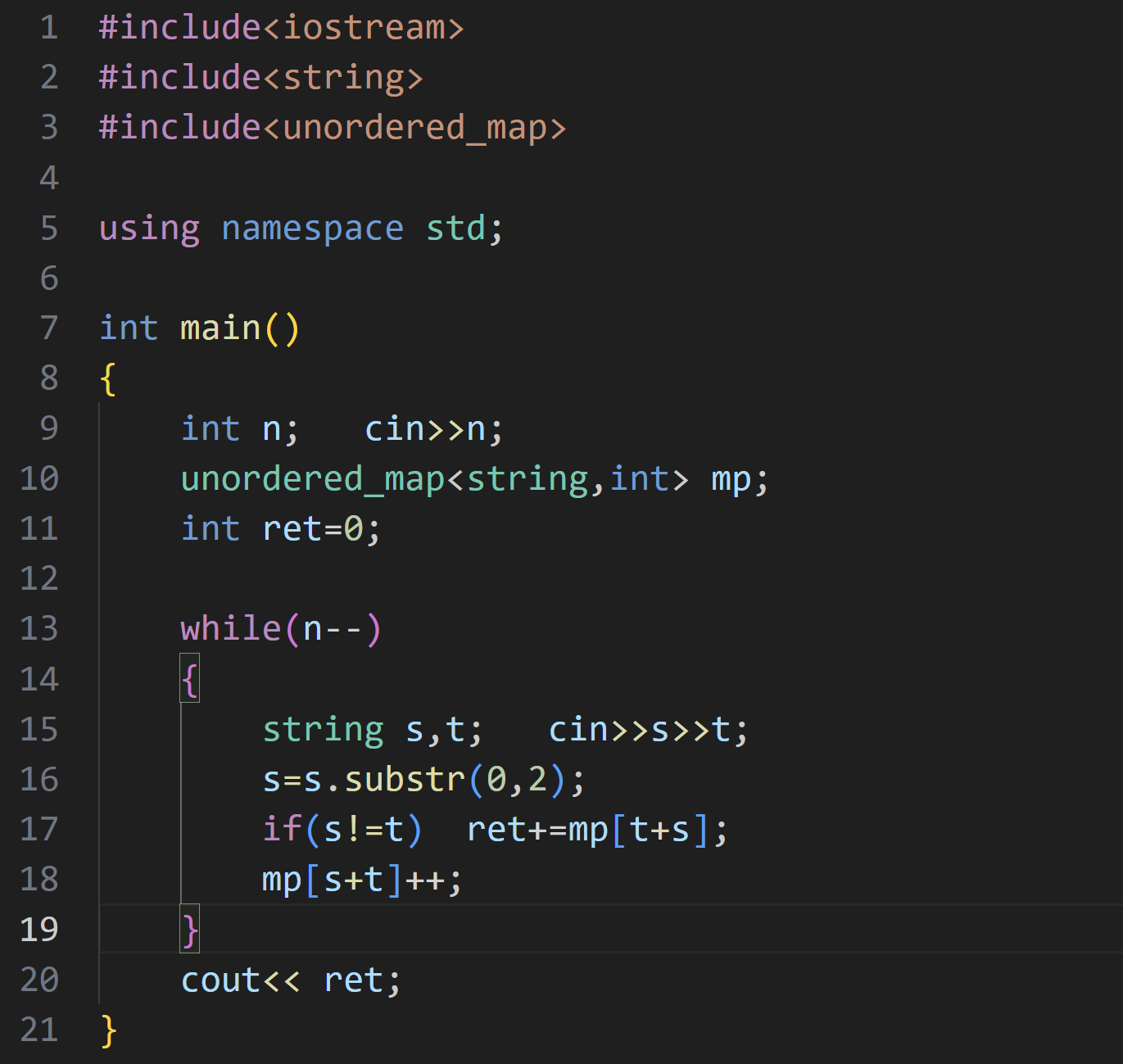
题目挺长的,简单来说就是要找出 "A城市名前两个字母"=="B州的编号" 并且 "B城市名前两个字母"=="A州的编号",这样 AB 成为一对,问一组中一共有几对
我们首先可以将 城市的前两个字母(t)和 州的编号 (s) 组成一个字符串(t+s),我们去找 s+t 的个数
代码展示:
结语:
ok了,关于算法竞赛中的数据结构知识就完结了,制作不易,内容较长,可以点个收藏,如果对你的学习有所帮助,关注我,我们一起学习进步
往期博客
1.算法_数据结构上
3.二叉树