排序和查找算法：插入排序、希尔排序、快速排序以及二分查找

一、排序和查找算法

|------|----------|-----|
| 名称 | 时间复杂度 | 稳定性 |
| 冒泡排序 | O（n^2） | 稳定 |
| 选择排序 | O（n^2） | 不稳定 |
| 插入排序 | O（n^2） | 稳定 |
| 希尔排序 | O（nlogn） | 不稳定 |
| 快速排序 | O（nlogn） | 不稳定 |

在排序之前我们先利用srand(time(NULL))函数生成随机数种子

cpp 复制代码

int InputArarry(int parray, int len)
{
    int i = 0;
    srand(time(NULL));
    
    for(i = 0; i < len; i++)
    {
        parray[i] = rand() % (len * 100);
    }

    return 0;
}

1.冒泡排序

相邻两个元素比较，大的一点点向后走，小的一点点向前走

关键代码示例：

cpp 复制代码

int BubbleSort(int parray, int len)
{
    int i = 0;
    int j = 0;
    int tmp = 0;

    for(j = 0; j < len-1; j++)
    {
        for(i = 0; i < len-1-j; i++)
        {
            if(parray[i] > parray[i+1])
            {
                tmp = parray[i];
                parray[i] = parray[i+1];
                parray[i+1] = tmp;
            }
        }
    }

    return 0;
}

2.选择排序

定义最小值下标，循环遍历比较，更新最小值下标，再交换数值

关键代码示例：

cpp 复制代码

int SelectSort(int parray, int len)
{
    int i = 0;
    int j = 0;
    int Min = 0;
    int tmp = 0;

    for(j = 0; j < len-1; j++)
    {
        Min = j;
        for(i = j+1; i < len; i++)
        {
            if(parray[i] < parray[Min])
            {
                Min = i;
            }
        }

        if(Min != j)
        {
            tmp = parray[j];
            parray[j] = parray[Min];
            parray[Min] = tmp;
        }
    }

    return 0;
}

3.插入排序

数据排列大致有序的场合下便于使用插入排序，将第一个元素看作一个有序数列，插入元素在这个有序数列中。

先将要插入的数据取出放入tmp；
前一个数据与tmp比较；
前一个数据大于tmp时，交换。

关键代码示例：

cpp 复制代码

int InsertSort(int parray, int len)
{
    int i = 0;
    int j = 0;
    int tmp = 0;
    
    for(j = 1; j < len; j++)
    {
        tmp = parray[j];
        for(i = j; i > 0 && parray[i-1] > tmp; i--)
        {
            parray[i] = parray[i-1];
        }
        parray[i] = tmp;
    }

    return 0;
}

4.希尔排序

基于插入排序的思想，在插入排序之前，将序列排成大致有序的数列，再整体进行插入排序

数组长度的一半作为步长，按步长将数组划分为几个小的数组；
划分后进行插入排序，直到不能划分后排序完成；（len / 2 == 0时无法再划分）

图示：

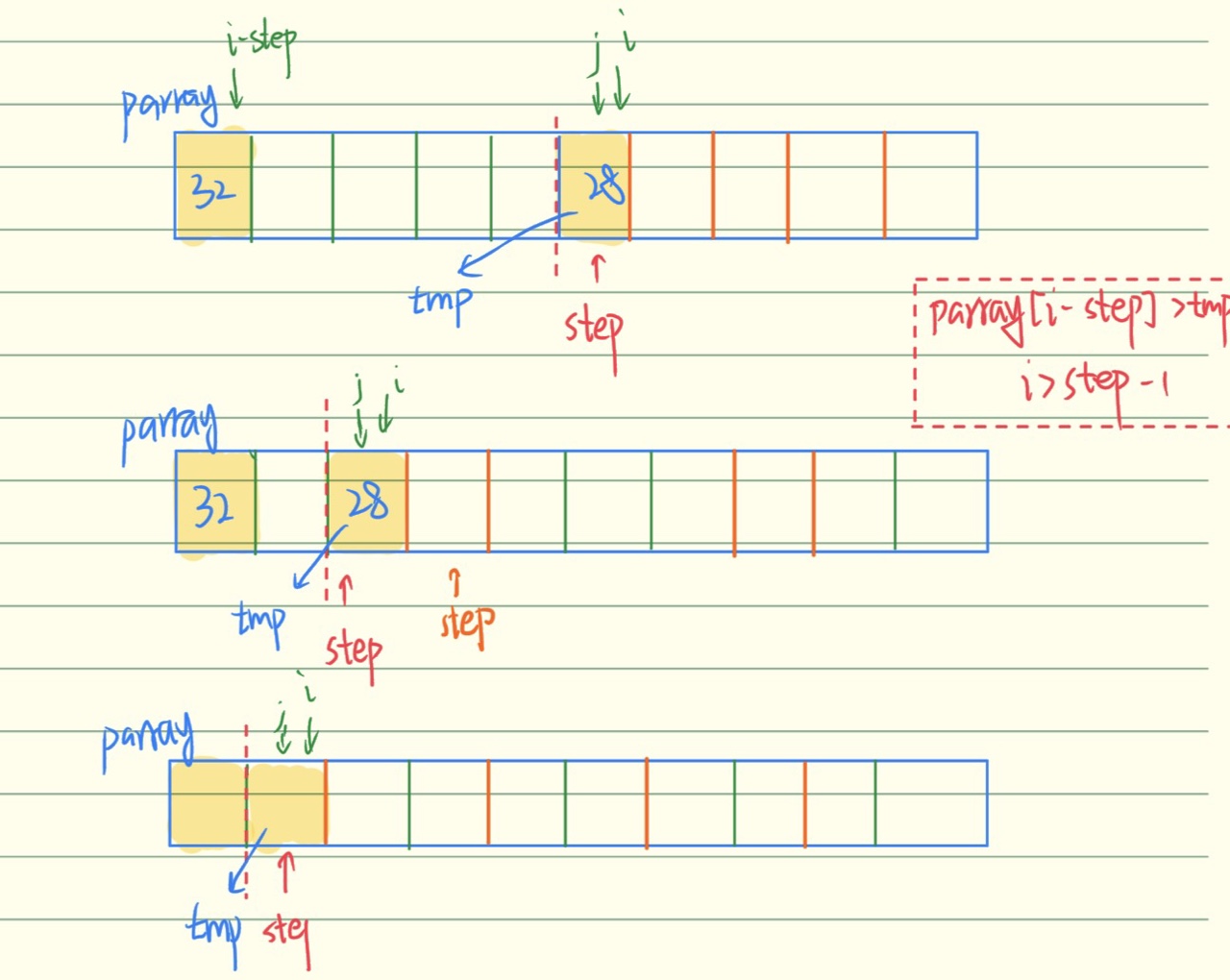
关键代码示例：

cpp 复制代码

int SellSort(int parray,int len)
{
    int i = 0;
    int j = 0;
    int step = 0;
    int tmp = 0;

    for(step = len / 2 ; step > 0; step /= 2)
    {
        for(j = step; j < len; j++)
        {
            tmp = parray[j];
            for(i = j; i > step-1 && parray[i-step] > tmp; i -= step)
            {
                parray[i] = parray[i-step]
            }
            parray[i] = tmp;
        }
    }

    return 0;
}

5.快速排序

选择最左边的数作为键值；
从后面选一个比键值小的数放前面；
从前面选一个比键值大的数放后面；
最终两个箭头相遇的位置放入键值，循环操作以上步骤，直到排序完成

图示：

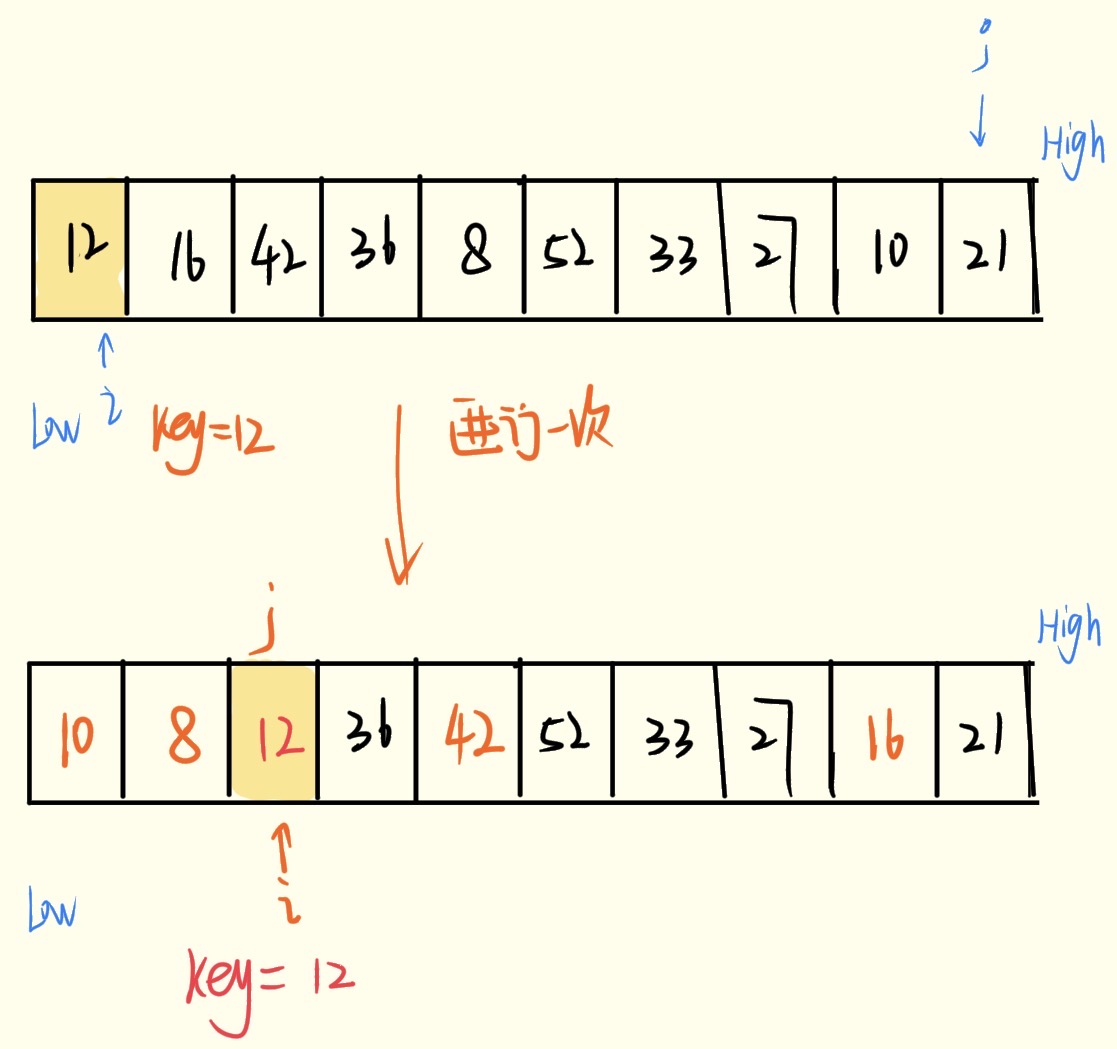
关键代码示例：

cpp 复制代码

int QuickSort(int parray, int Low, int High)
{
    int i = 0;
    int j = 0;
    int key = 0;

    i = Low;
    j = High;
    key = parray[Low];

    while(i < j)
    {
        while(i < j && parray[j] >= key)
        {
            j--;
        }
        parray[i] = parray[j];

        while(i < j && parray[i] <= key)
        {
            i++;
        }
        parray[j] = parray[i];
    }
    parray[i] = key;

    if(Low < i-1)
    {
        QuickSort(parray, Low, i-1);
    }
    if(i+1 < High)
    {
        quickSort(parray, i+1, High);
    }

    return 0;
}

二、二分查找（折半查找）

前提是数据排列必须有序；时间复杂度为O(logn)

图示：

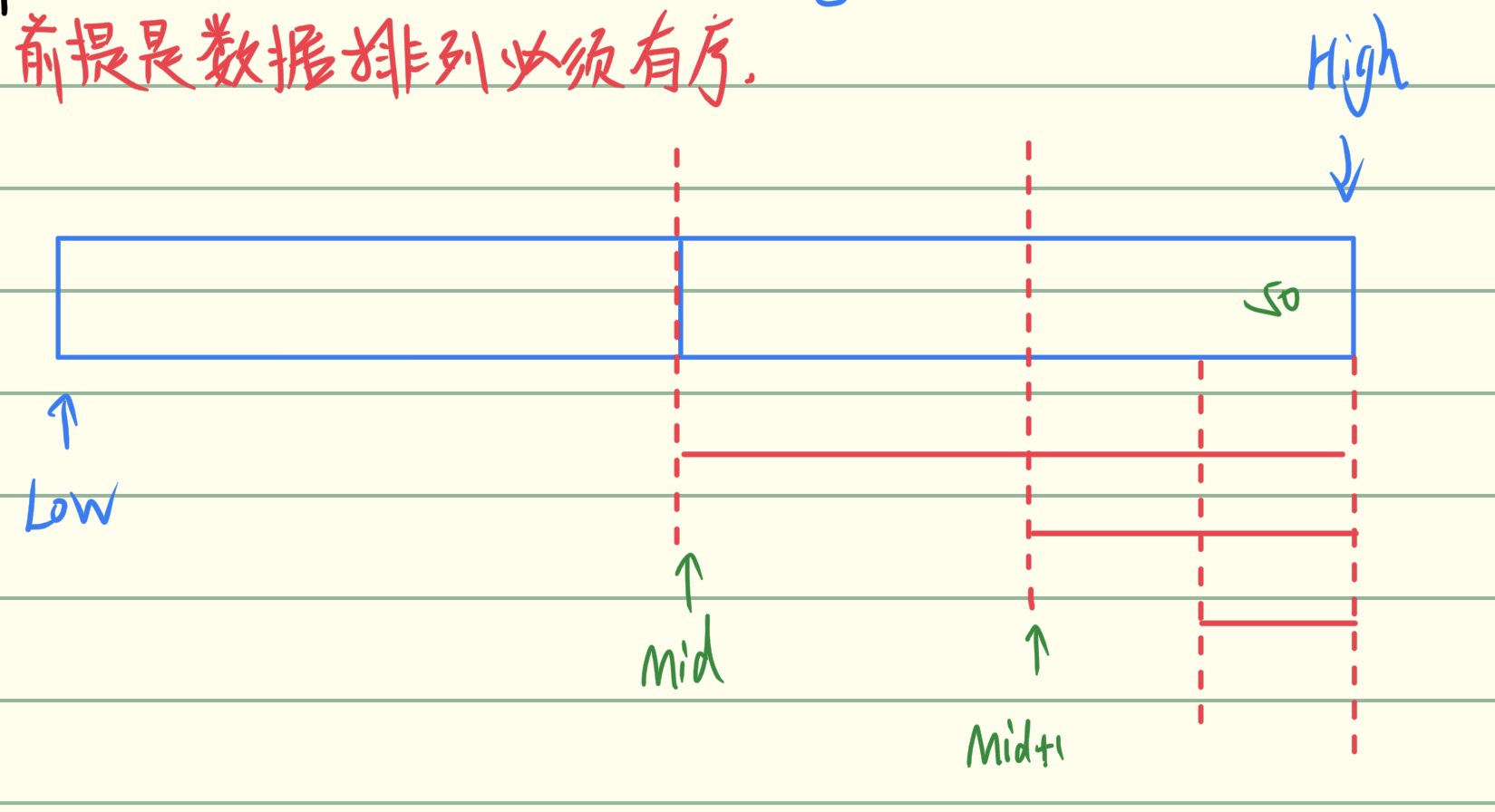
关键代码示例：

cpp 复制代码

int MidSearch(int parray, int Low, int High, int TmpData)
{
    int Mid = 0;

    if(Low > High)
    {
        return -1;
    }
    Mid = (Low + High) / 2;

    if(parray[Mid] < TmpData)
    {
        return MidSearch(parray, Mid+1, High, Tmpdata);
    }
    else if(parray[Mid] > Tmpdata)
    {
        return MidSearch(parray, Low, Mid-1, TmpData);
    }
    else if(parray[Mid] == Tmpdata)
    {
        return Mid;
    }
}