一、研究动机
论文标题: NeuralChain-of-Thought Search: Searching the Optimal Reasoning Path to Enhance Large Language Models
论文地址: https://arxiv.org/pdf/2601.11340
作者背景: 中山大学
代码仓库: https://github.com/MilkThink-Lab/Neural-CoT-Search
1.1 问题背景
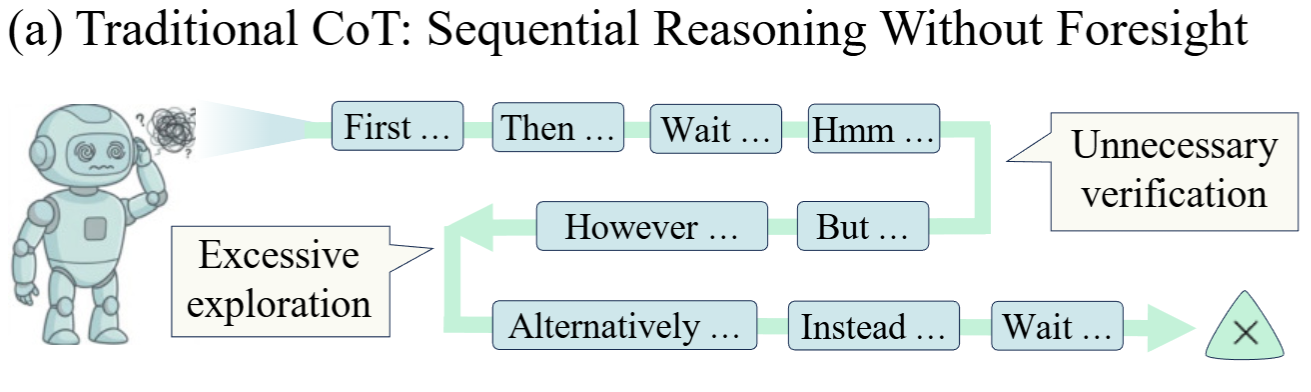
研究人员认为,当前大模型存在推理路径规划能力不足的问题,即只擅长逐步生成推理步骤,缺乏对整体推理方向的前瞻思维,容易陷入低效的推理模式:
- 频繁输出"Wait"、"Hmm"等反思性 token,触发不必要的验证步骤
- 陷入过度的分支探索,导致推理冗余
- 无法预见最优推理方向,走入次优路径
这就像一个人在解决问题时,只顾着埋头往前走,却不抬头看看是否走在正确的道路上。
1.2 关键发现:混合引导实验
这不禁让我们设想:如果模型能在思考的关键转折点上做更充分的搜索,效果会不会更好?
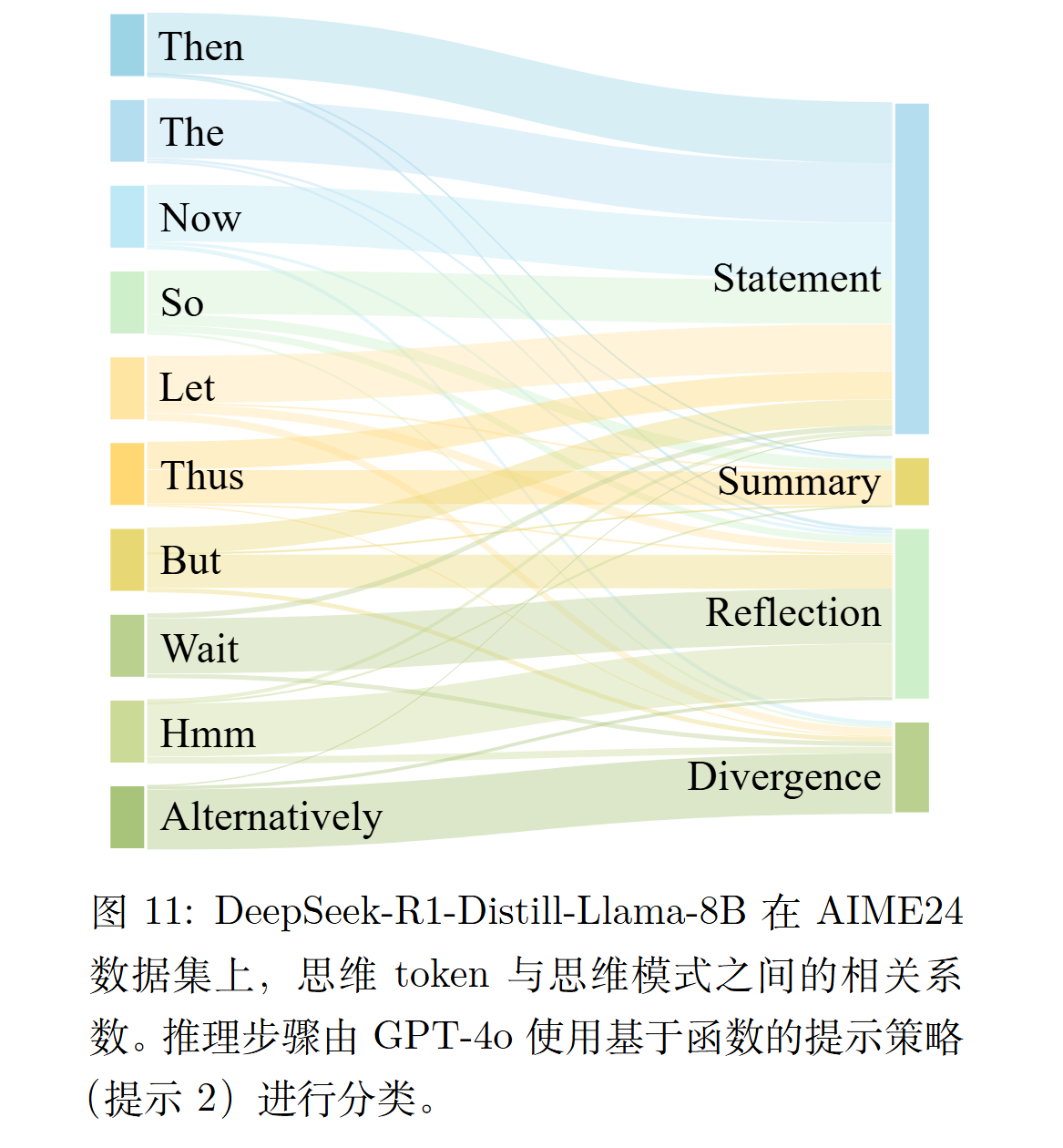
观察 CoT 数据特点不难发现,模型通常会在每个决策点处,先吐出一个"开头词/转向词"来决定下一步的语气与方向,比如:
- "Wait" → 往反思/检查的模式走
- "Then / So" → 往继续推导的模式走
- "Alternatively" → 往分支探索走
于是作者设计了一个巧妙的实验:以 7B 模型为研究对象,要求模型推理时用"\n\n"作为每个推理步骤之间的间隔,然后在每个推理步骤的开头,使用更大的模型(32B)为其生成一个引导 token,7B 模型继续完成后续推理
实验结果令人惊讶:
- 这些引导 token 仅占总输出的 2.9%
- 却带来了平均 6.2% 的准确率提升
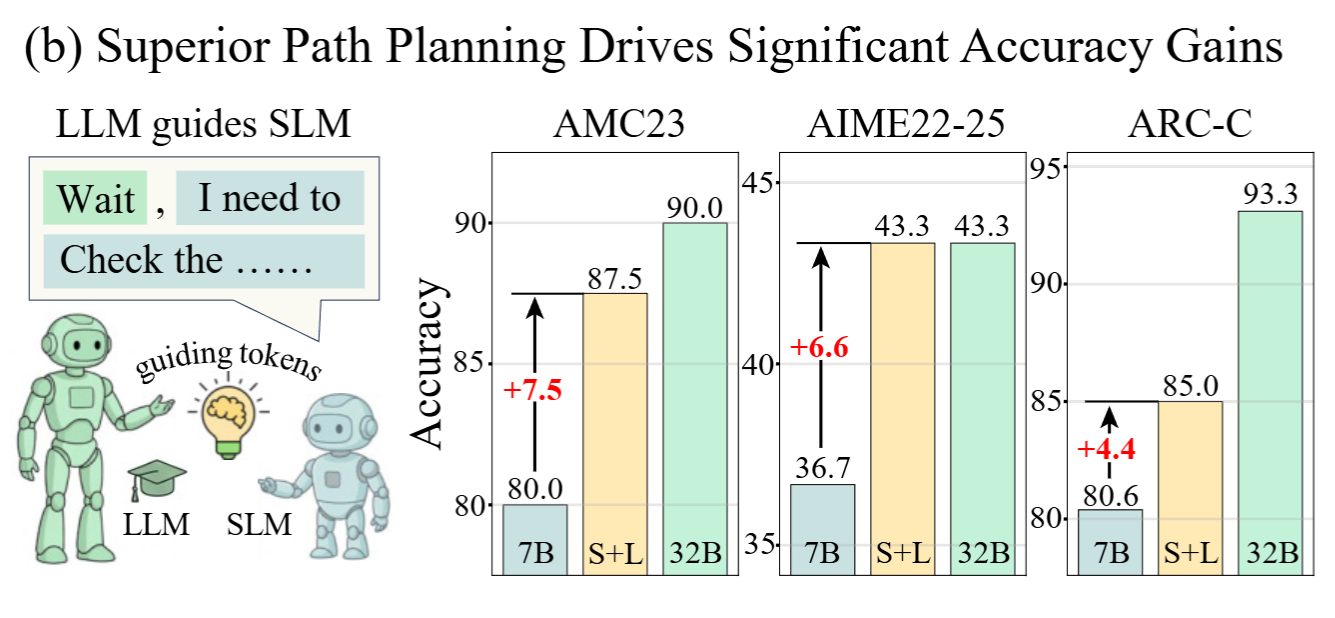
这说明小模型具备足够的执行能力,但缺乏高层次的战略规划能力。更重要的是,这一结论验证了开头的设想:存在更优的推理关键 token 让模型推理效果更好,推理任务可被视作路径搜索问题
二、方法原理与实现
2.1 整体框架
论文提出了 Neural Chain-of-Thought Search (NCoTS) 框架,其核心思想是:搜索如何思考(Search How to Think)。
与传统方法顺序生成推理步骤不同,NCoTS 在完成每一个推理步骤后会"停下来思考"------评估下一步该采取什么样的思维模式,然后选择最优方向继续前进。
整体流程包含四个阶段:
- 暂停生成 :检测到步骤分隔符(
\n\n)时暂停 - 前瞻模拟:将所有候选推理操作符投影到未来上下文
- 启发式评估:用双因子函数评估每个方向的成功概率和效率
- 策略选择:基于综合得分采样最优操作符,恢复生成
2.2 核心概念定义
决策点
NCoTS 将推理链分解为一系列离散的步骤,步骤之间用 \n\n 分隔符标记。这些分隔符的位置就是"决策点"------模型需要决定下一步走向何方的关键节点。
推理操作符
在每个决策点,模型会输出一个"思维 token"来指示后续步骤的逻辑方向。这些 token 被定义为推理操作符,组成一个有限集合:
O = {"Wait", "So", "Then", "Let", "Thus", "Therefore", "The", "Alternatively", ...}推理架构
操作符的序列 α = (o₁, o₂, ..., oₜ) 定义了推理的高层次结构,论文称之为"推理架构"。NCoTS 的目标就是找到最优架构 α*,在最大化准确率的同时最小化序列长度。
2.3 双因子启发式函数
这是 NCoTS 的核心创新------用一个复合启发式函数 H(hₜ, o) 来评估在当前状态下应用操作符 o 的效果。
路径潜力估计
目标:预测特定推理方向导致正确解的概率
实现:一个线性投影层,将最后的隐藏状态映射到操作符集合的 logits
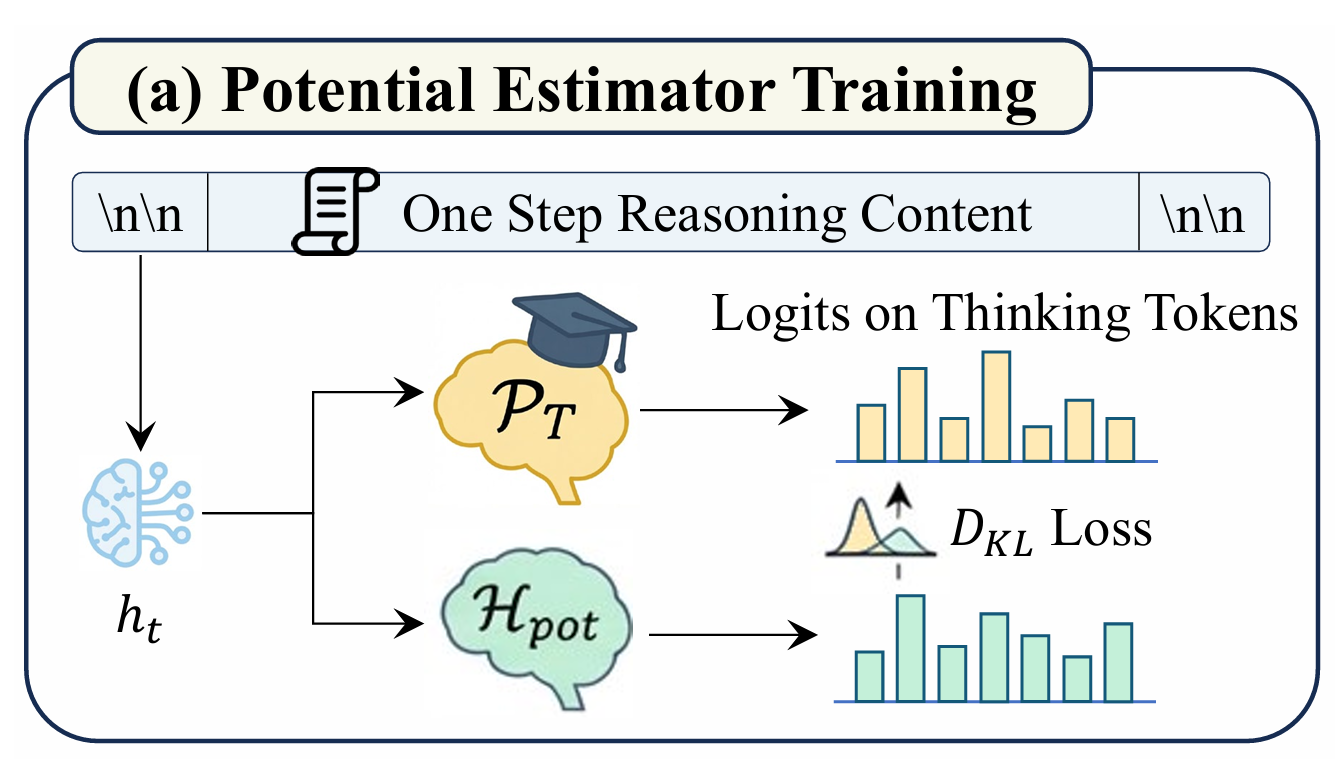
训练:通过策略蒸馏从更大的教师模型学习。将教师模型在操作符上的概率分布视为专家策略 P_T,最小化 KL 散度:
L pot = E h t ∼ D [ D KL ( P T ( h t ) ∥ H pot ( h t ) ) ] \mathcal{L}{\text{pot}} = \mathbb{E}{h_t \sim \mathcal{D}} \left[ D_{\text{KL}}\Big( P_T(h_t) \;\big\|\; \mathcal{H}_{\text{pot}}(h_t) \Big) \right] Lpot=Eht∼D[DKL(PT(ht) Hpot(ht))]
直觉:大模型拥有更强的高层次规划能力,通过蒸馏将这种能力迁移到搜索过程中,充当"正确性指南针"。
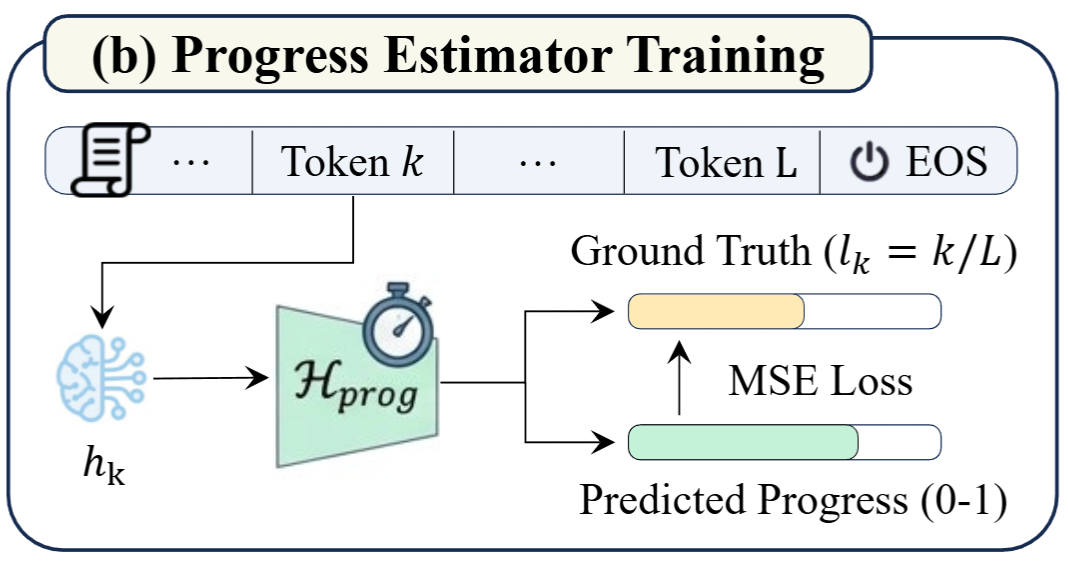
推理进度估计
目标:估计推理路径的效率,预测当前已完成解决方案的比例。
实现:一个线性回归头,将隐藏状态映射到一个标量值(比如当前进度: 80%)
训练:在 token 级别的密集监督任务上训练。对于路径中位置 k 的每个 token,其进度标签为 lₖ = k/L,最小化均方误差:
L prog = E ( h k , l k ) ∼ D [ ∥ H prog ( h k ) − l k ∥ 2 ] \mathcal{L}{\text{prog}} = \mathbb{E}{(h_k, l_k) \sim \mathcal{D}} \left[ \left\| \mathcal{H}_{\text{prog}}(h_k) - l_k \right\|^2 \right] Lprog=E(hk,lk)∼D[∥Hprog(hk)−lk∥2]
直觉:通过最大化预测进度,搜索算法会偏好那些能显著推进推理状态的操作符,有效惩罚冗长或循环的步骤
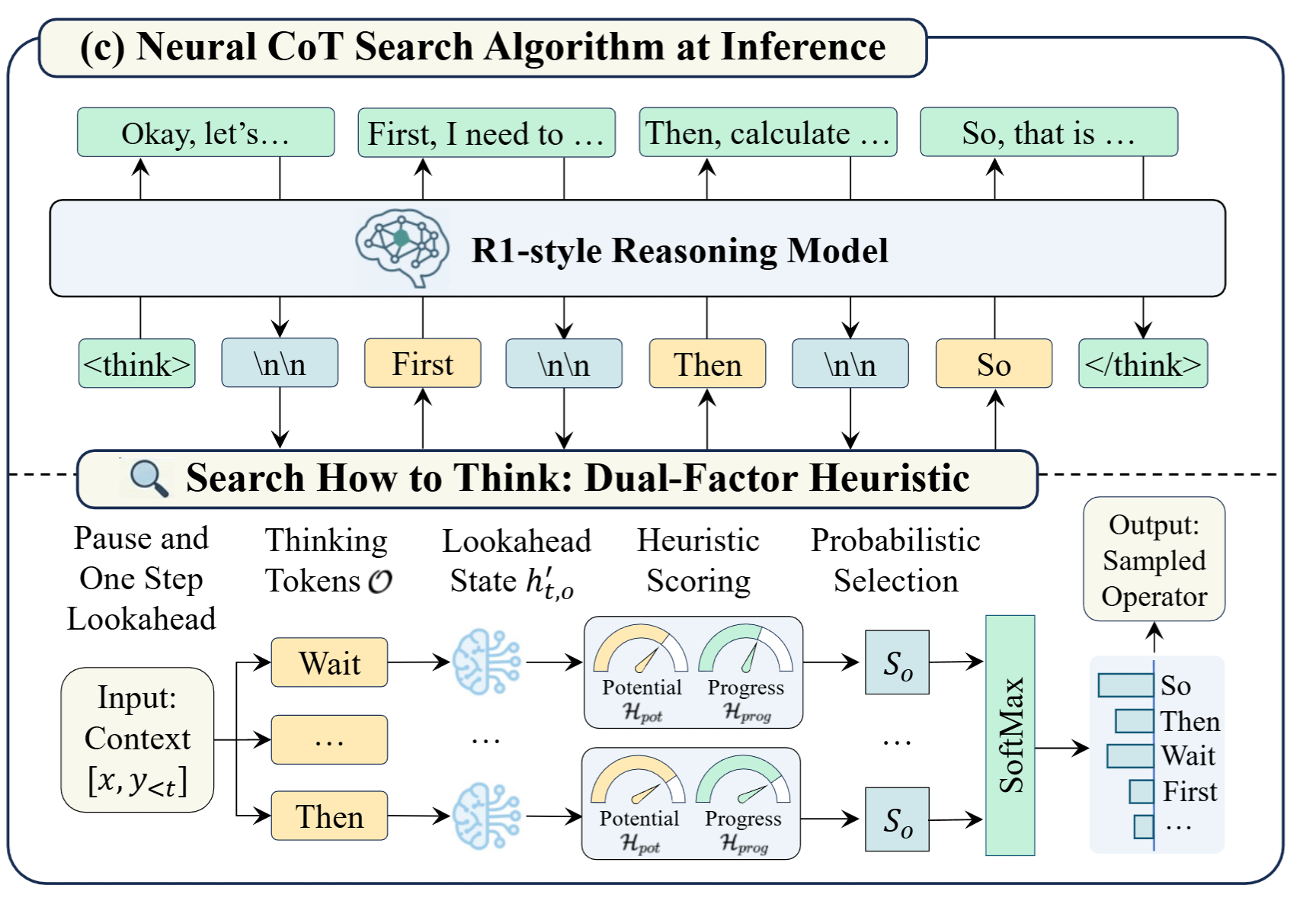
2.4 搜索算法
单步前瞻
在决策点 t,对于每个候选操作符 o ∈ O,将其附加到当前 KV 缓存来模拟下一步。由于思维 token 决定了思维模式,这种轻量级前瞻足以捕获分支的语义轨迹,而无需完整生成整个步骤。
启发式评分
对每个分支计算综合得分,整合潜力和效率:
S ( o ) = H potential ( h t , o ) ⏟ 成功潜力 + λ ⋅ H progress ( h t , o ′ ) ⏟ 效率进度 S(o) = \underbrace{\mathcal{H}{\text{potential}}(h_t, o)}{\text{成功潜力}} + \lambda \cdot \underbrace{\mathcal{H}{\text{progress}}(h'{t,o})}_{\text{效率进度}} S(o)=成功潜力 Hpotential(ht,o)+λ⋅效率进度 Hprogress(ht,o′)
其中 λ 是控制简洁性权重的超参数。
概率选择
使用 Softmax 函数将得分转换为概率分布:
P search ( o ∣ h t ) = exp ( S ( o ) / τ ) ∑ o ′ ∈ O exp ( S ( o ′ ) / τ ) P_{\text{search}}(o|h_t) = \frac{\exp\left( S(o) / \tau \right)}{\sum_{o' \in \mathcal{O}} \exp\left( S(o') / \tau \right)} Psearch(o∣ht)=∑o′∈Oexp(S(o′)/τ)exp(S(o)/τ)
从该分布中 采样 最终操作符 o*,保证选择的推理方向既策略合理又计算高效,并保留一定的随机性以提高探索能力
三、实验结果
3.1 实验设置
数据集:四个多样化基准测试
- AMC23:美国数学竞赛题目,测试复杂数学推理
- ARC-C:抽象推理挑战,测试常识推理
- GPQA:研究生级问答,测试知识密集型推理
- GSM8K:小学数学题,测试多步算术推理
模型:DeepSeek-R1-Distill-Qwen 系列(1.5B、7B、14B、32B)
评估指标:
- 准确率(Acc)
- 平均生成长度(Length)
- 效率指标(η):综合衡量性能提升与计算节省的复合指标
η = ( A new A original ) 2 ⋅ L original L new \eta = \left( \frac{A_{\text{new}}}{A_{\text{original}}} \right)^2 \cdot \frac{L_{\text{original}}}{L_{\text{new}}} η=(AoriginalAnew)2⋅LnewLoriginal
3.2 主要结果
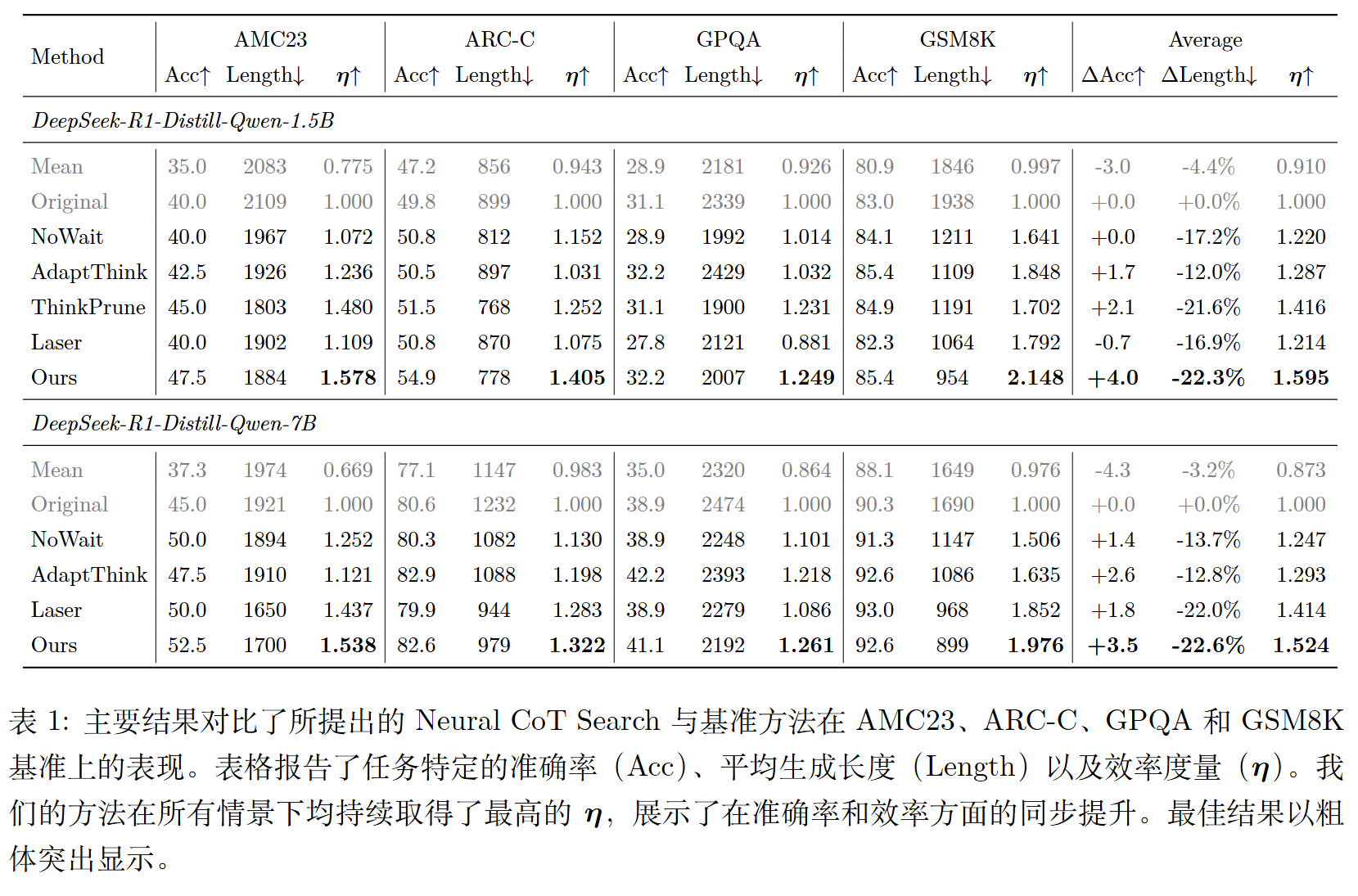
核心发现:
- 帕累托改进:NCoTS 同时提升了准确率并降低了生成长度,实现了真正的双赢
- 最高效率:在所有设置下,NCoTS 一致取得最高的效率指标 η
- 显著压缩:在 GSM8K 上,1.5B 模型的生成长度减少超过 50%,同时准确率仍有提升
- 任务适应性:在推理密集型任务(如 AMC23、GSM8K)上效率提升最大
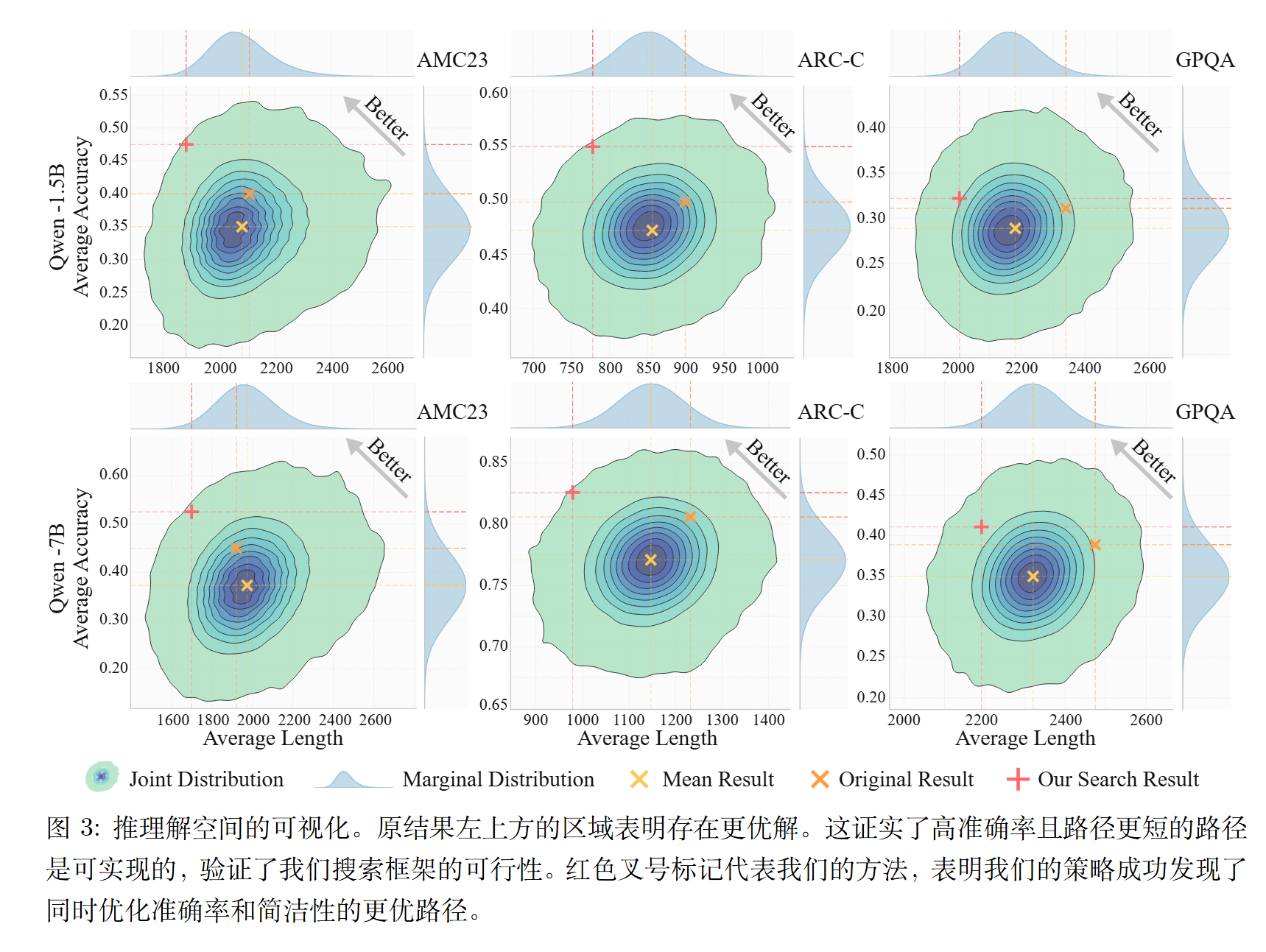
3.3 解空间可视化
论文通过随机搜索实验绘制了"准确率-长度"的密度热力图,揭示了四个关键发现:
- 操作符选择导致高方差:不同操作符选择会导致截然不同的结果
- 标准解码次优:原始基线远未达到理论性能边界
- 优质路径存在:存在同时具有更高准确率和更短长度的帕累托优质解
- 优质解稀疏:这些优质路径在解空间中非常稀疏,需要有针对性的搜索
3.4 消融实验
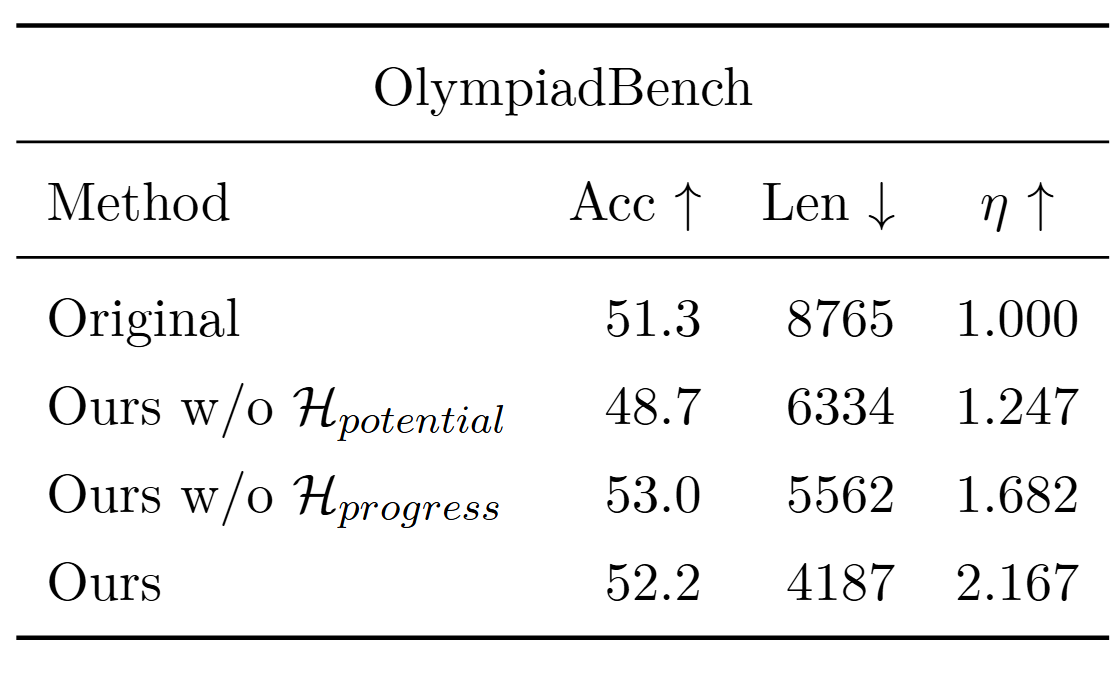
两个估计器各有独特贡献:
- 潜力估计器确保正确性
- 进度估计器优化简洁性
- 二者协同才能达到最佳效果
四、后续研究方向
4.1 多语言与创意任务扩展
当前的操作符集合主要针对英语 STEM 推理任务优化。未来可以:
- 为不同语言设计特定的思维 token
- 针对创意写作等任务重新校准操作符集合
4.2 超越教师监督
当前的潜力估计器依赖教师模型监督,理论上受限于教师的规划能力。未来可以:
- 采用强化学习使模型能够自我改进
- 探索超越教师分布的更优策略
4.3 动态决策点检测
当前使用静态的换行符作为决策点分隔符,可能过于僵化。未来可以:
- 基于熵值动态触发决策点
- 根据推理难度自适应调整搜索频率
4.4 全局搜索机制
当前采用局部单步前瞻策略,在极端复杂场景下限制了长期规划能力。未来可以:
- 探索类似 MCTS 的全局搜索机制
- 在计算开销和规划深度之间寻找平衡
五、启发与思考
5.1 思维 token 的控制机制作用
论文的一个深刻洞察是:思维 token 不仅仅是表面的前缀,而是控制下一步思维模式的机制。
就像人类在复杂推理时会动态切换思维模式(陈述、总结、反思、探索),LLM 也需要这种能力。"Wait"触发反思,"Then"推进执行,"Alternatively"开启探索。选择正确的思维 token 就是选择正确的思维模式。
5.2 "下一个 token 预测"的局限性
论文揭示了一个根本性问题:高效推理的瓶颈在于下一个 token 预测的近视性。
模型在生成每个 token 时只看到局部信息,无法预见整体推理路径。这就需要为模型赋予"预见能力"------不是预测下一个 token 是什么,而是规划"该怎么思考"。
5.3 搜索与生成的统一
NCoTS 将推理过程从纯粹的"生成"转变为"搜索+生成"的混合范式:
- 在宏观层面搜索最优推理架构
- 在微观层面执行具体推理步骤
这种分层思想可能对未来的 LLM 设计有启发意义。
5.4 效率与正确性的平衡
传统上,缩短推理长度往往会损害准确率。NCoTS 证明了通过智能搜索,可以同时优化两个目标。这提示我们:冗余推理本身就是一种错误,精简的推理往往更准确。
5.5 轻量级增强的有效性
NCoTS 新增的参数量仅占模型的 0.0017%,却带来了显著的性能提升。这表明:对现有模型的轻量级增强可能比从头训练更高效。这个思路可以推广到其他模型能力增强场景。