目录
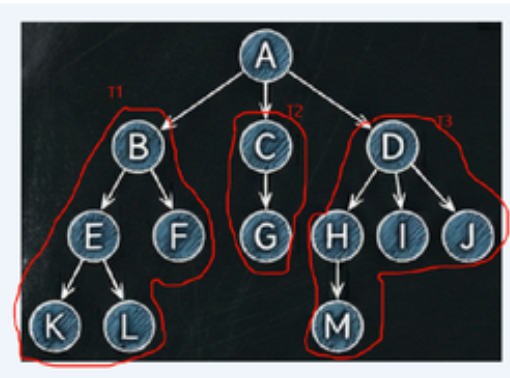
一、树的定义:
树是n(n>=0)个结点的有限集会
当n=0时,称为空树
当n>0时,满足:
1.有且仅有一个根节点(root)
2.其余节点可分为m(m>=0)个互不相交 的有限集合,每个集合本身也是一颗树,称为根的子树(Subtree)
概念:
1.节点的度---节点所拥有的子树的个数,如上图:b的度为2,a的度为3
2.树的度---节点中最大的度,如上图:树的度为3
3.叶子(终端节点)---度为0
4.分支节点(内部节点或非终端节点)---度不为0
节点之间的关系:
1.双亲与孩子--节点的子树的根称为该节点的孩子,该节点称为孩子的双亲
2.祖先与子孙---祖先:从根到该节点所经分支上的所有节点,子孙:以某节点为根的子树中的任一节点
3.兄弟与堂兄弟---同一个双亲 的节点互为兄弟,双亲在同一层的节点互为堂兄弟
二、二叉树
二叉树具有以下五种基本形态:
1.空二叉树
2.只有一个根节点
3.根节点只有左子树
4.根节点只有右子树
5.根节点既有左子树又有右子树
1.满二叉树:
每个分支节点都有左子树和右子树,叶子节点都在同一层且都是满的
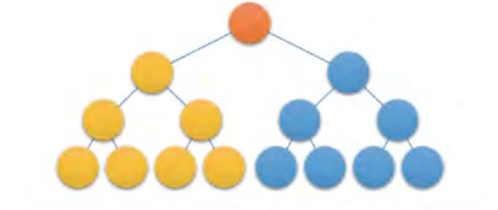
2.完全二叉树:
如果其每个节点的编号与满二叉树 中编号从 1 到 n 的节点一一对应,可以不满
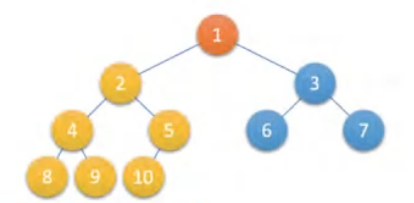
重要性质:

3.二叉树的遍历
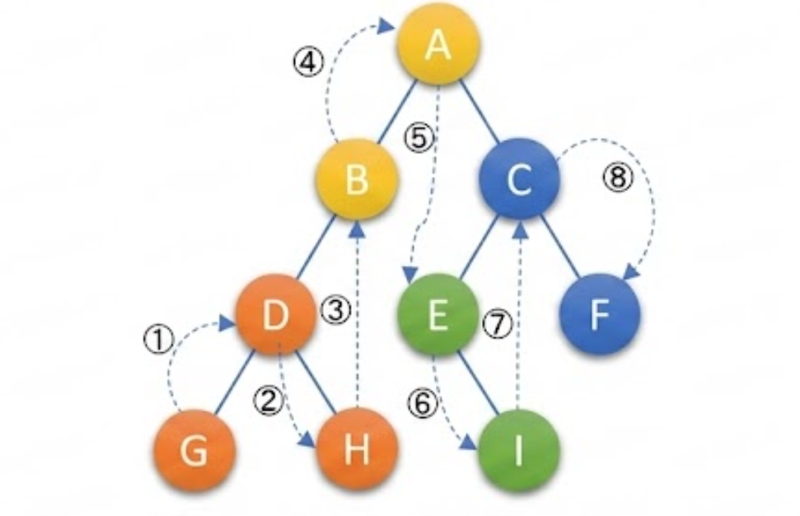
a.前序遍历:
根 → 左 → 右
先访问根结点,再递归遍历左子树,最后右子树
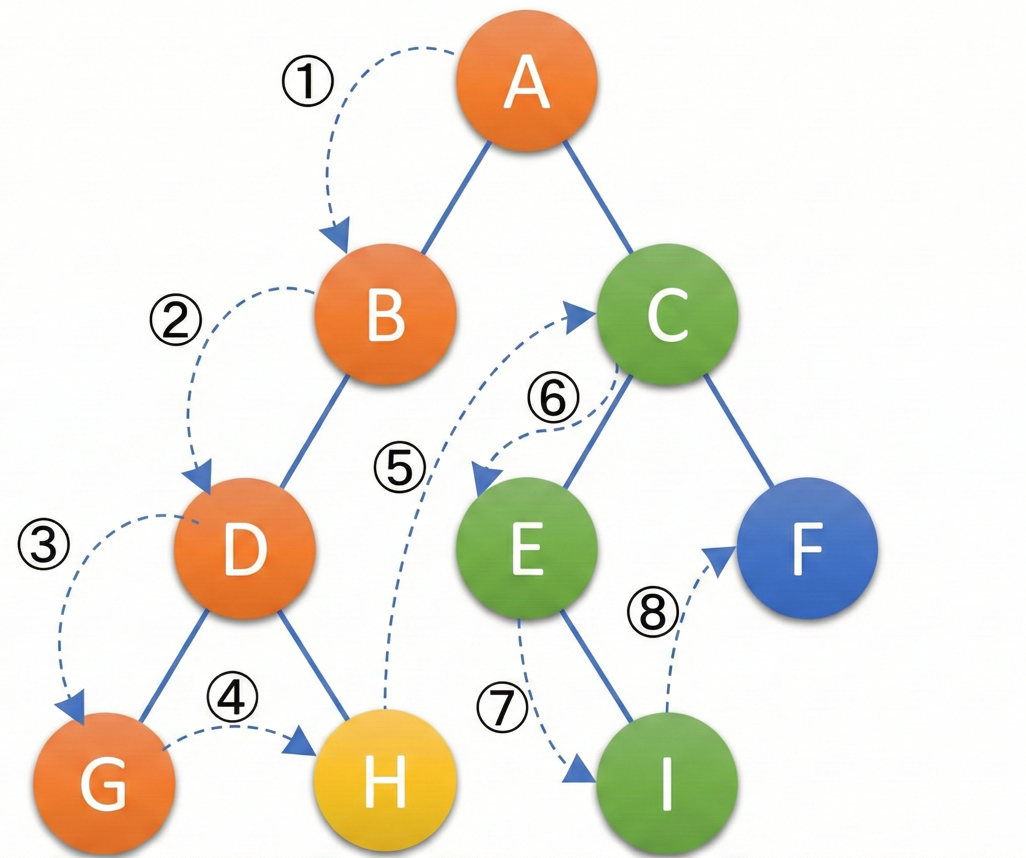
b.中序遍历:
左 → 根 → 右
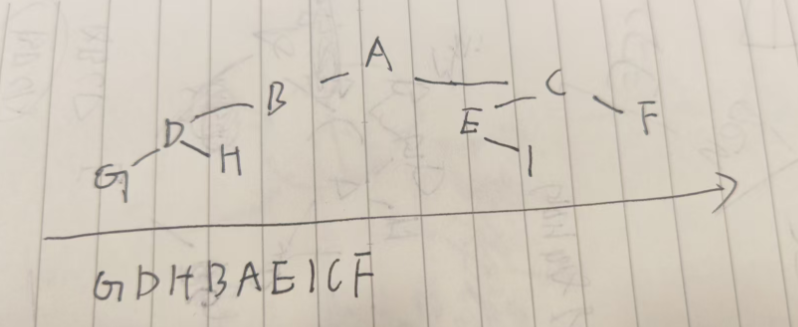
简易方法:把这个二叉树展平,把字母放在一条线上,然后从左到右依次写出来就是GDHBAEICF
注意:写算法的时候还是得知道它的原理是先递归遍历左子树,再访问根,最后右子树
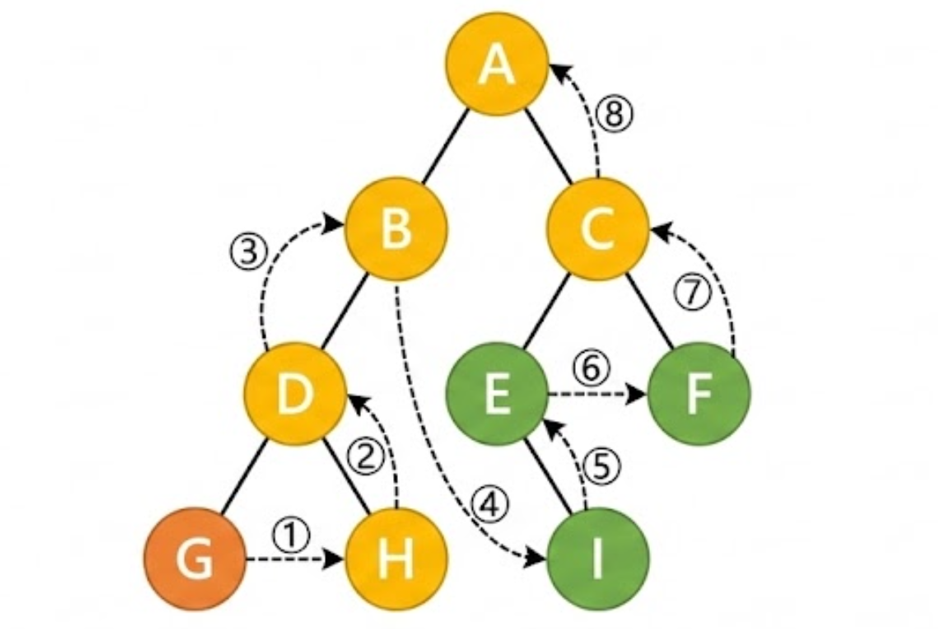
c.后序遍历
左 → 右 → 根
先递归遍历左右子树,最后访问根结点
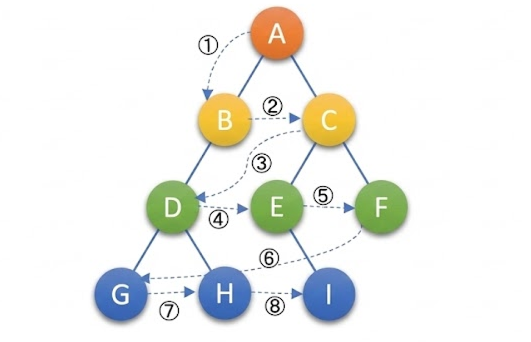
d.层序遍历
从上到下、从左到右
按层次逐层访问,通常借助队列实现
三、二叉树的算法实现
二叉树的结构体:
typedef int data_t; typedef struct btree { data_t data; //数据域 struct btree *pl; //left ---左子树 struct btree *pr; //right ---右子树 }btree_t;
相关算法:
主要是利用递归实现
1.创建二叉树:
和操作数组差不多
char tree_seq[] = "ABDG##H###CE#I##F##";
int idx = 0; //索引
// 常见操作函数
btree_t * create_btree() // 创建二叉树
{
//1.获取数据
char data = tree_seq[idx];
idx++;
if (data == '#')
{
return NULL;//NULL 表示结束
}
//2.创建新节点 malloc
btree_t *new = malloc(sizeof(btree_t));
if (new == NULL)
{
printf("%s: malloc fail!\n",__func__);
return NULL;
}
new->data = data;//tree_seq[idx]; //根
new->pl = create_btree(); //左
new->pr = create_btree(); //右
return new;
} 2.前序遍历:
原理:根左右,递归即可
//函数 最终返回后,返回的是根节点
int pre_order_traverse(btree_t *t) //传根节点的地址
{
//结束条件 t == NULL
if (t == NULL)
{
return 0;
}
printf("%c ",t->data);//根
pre_order_traverse(t->pl); //左子树 //左
pre_order_traverse(t->pr);// 右子树 //右
return 0;
}3.中序遍历:
左根右
注意:递归函数名一定得和写的一致
int in_order_traverse(btree_t *t) // 中序遍历
{
//结束条件 t == NULL
if (t == NULL)
{
return 0;
}
in_order_traverse(t->pl); //左子树 //左
printf("%c ",t->data);//根
in_order_traverse(t->pr);// 右子树 //右
return 0;
}4.后序遍历:
左右根
int post_order_traverse(btree_t *t) // 后序遍历
{
//结束条件 t == NULL
if (t == NULL)
{
return 0;
}
post_order_traverse(t->pl); //左子树 //左
post_order_traverse(t->pr);// 右子树 //右
printf("%c ",t->data);//根
return 0;
}5.销毁二叉树:
后续遍历,然后销毁
int btree_destroy(btree_t *t) // 销毁二叉树
{
if (t == NULL)
{
return -1;
}
//递归 --- 后序方式
//左右根
btree_destroy(t->pl);//左
btree_destroy(t->pr);//右边
free(t);
return 0;
}