决策树三大核心算法详解：ID3、C4.5与CART

一、ID3算法：以信息增益为核心

示例：基于14天的天气数据（特征：天气、温度、湿度、有风；标签：是否打球），演示三种算法的分裂逻辑。

日期	天气（outlook）	温度（temperature）	湿度（humidity）	有风（windy）	打球（play）
1	sunny	hot	high	FALSE	no
2	sunny	hot	high	TRUE	no
3	overcast	hot	high	FALSE	yes
4	rainy	mild	high	FALSE	yes
5	rainy	cool	normal	FALSE	yes
6	rainy	cool	normal	TRUE	no
7	overcast	cool	normal	TRUE	yes
8	sunny	mild	high	FALSE	no
9	sunny	cool	normal	FALSE	yes
10	rainy	mild	normal	FALSE	yes
11	sunny	mild	normal	TRUE	yes
12	overcast	mild	high	TRUE	yes
13	overcast	hot	normal	FALSE	yes
14	rainy	mild	high	TRUE	no

1. 核心逻辑

ID3算法通过信息增益选择分裂特征，信息增益越大，说明该特征降低数据不确定性的能力越强，越适合作为分裂节点。

2. 关键计算步骤

（1）计算类别熵（初始不确定性）

标签"是否打球"的熵：14天中9天打球（yes）、5天不打球（no），熵值公式为：

H(U) = -\\sum_{i=1}\^{n} p_i log_2 p_i

代入计算：

H = -\\frac{9}{14}log_2\\frac{9}{14} - \\frac{5}{14}log_2\\frac{5}{14} ≈ 0.940

（2）计算各特征的信息增益

以"天气"特征为例：

天气分为sunny（5天）、overcast（4天）、rainy（5天）
各子组熵值：
- sunny：2天yes、3天no → $$H=-\frac{2}{5}log_2\frac{2}{5} - \frac{3}{5}log_2\frac{3}{5}≈0.97$$
- overcast：4天yes、0天no → $$H=0$$
- rainy：3天yes、2天no → $$H=-\frac{3}{5}log_2\frac{3}{5} - \frac{2}{5}log_2\frac{2}{5}≈0.97$$
天气特征的平均熵：$$\frac{5}{14}×0.971 + \frac{4}{14}×0 + \frac{5}{14}×0.971≈0.69$$
信息增益：$$0.940 - 0.693 = 0.24$$

（3）选择最优特征

计算所有特征的信息增益后排序：

天气（0.247）> 湿度（0.151）> 有风（0.048）> 温度（0.029）

因此，ID3算法选择"天气"作为根节点分裂特征。

（4）递归分裂各子节点

根节点"天气"分裂为三个子节点，分别处理如下：

overcast子节点：含4条数据（日期3、7、12、13），均为"yes"（打球），节点纯度100%，无需继续分裂，直接作为叶子节点，输出结果"yes"。
sunny子节点：含5条数据（日期1、2、8、9、11），类别分布为2条"yes"、3条"no"，需基于剩余特征（温度、湿度、有风）计算信息增益，选择最优分裂特征。步骤1：计算该子节点的初始熵（仅基于5条数据）：$$H = -\frac{2}{5}log_2\frac{2}{5} - \frac{3}{5}log_2\frac{3}{5}≈0.971$$。
步骤2：计算剩余特征的信息增益（以"湿度"为例，其余特征增益更低）：湿度取值：high（4条：1yes、3no）、normal（1条：1yes）；
子组熵：high组$$H≈0.811$$，normal组$$H=0$$；
平均熵：$$\frac{4}{5}×0.811 + \frac{1}{5}×0≈0.649$$；
信息增益：$$0.971 - 0.649 = 0.322$$（为该子节点下最大增益）。

步骤3：选择"湿度"作为分裂特征，分裂为两个子节点：湿度=high：4条数据（1yes、3no），输出结果"no"（多数类）；

湿度=normal：1条数据（1yes），输出结果"yes"。

rainy子节点：含5条数据（日期4、5、6、10、14），类别分布为3条"yes"、2条"no"，基于剩余特征（温度、湿度、有风）计算信息增益。步骤1：计算该子节点的初始熵：$$H = -\frac{3}{5}log_2\frac{3}{5} - \frac{2}{5}log_2\frac{2}{5}≈0.971$$。

步骤2：计算剩余特征的信息增益（"有风"特征增益最大）：有风取值：FALSE（3条：3yes）、TRUE（2条：2no）；

子组熵：FALSE组$$H=0$$，TRUE组$$H=0$$；

平均熵：$$\frac{3}{5}×0 + \frac{2}{5}×0 = 0$$；

信息增益：$$0.971 - 0 = 0.971$$。

步骤3：选择"有风"作为分裂特征，分裂为两个子节点：有风=FALSE：3条数据（3yes），输出结果"yes"；

有风=TRUE：2条数据（2no），输出结果"no"。

（5）ID3决策树可视化

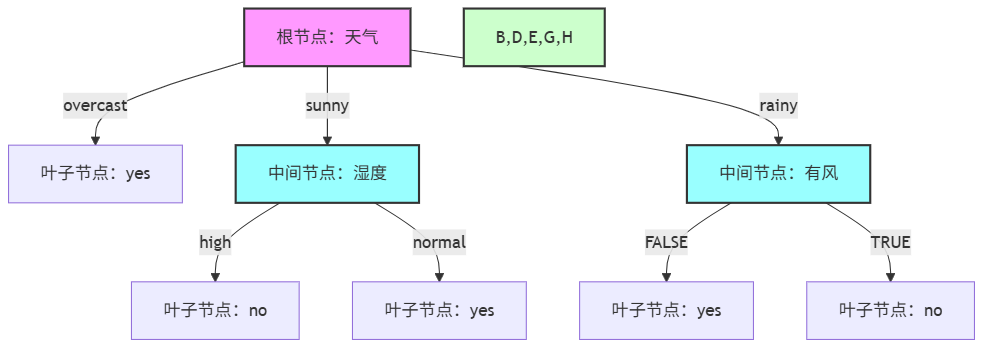
3. 优缺点

✅ 优点：计算简单，直观易懂，能快速找到高区分度特征。
❌ 缺点：偏好取值多的特征（如编号类特征），易过拟合；不支持连续值特征。

三、C4.5算法：用信息增益率修正偏差

1. 核心逻辑

C4.5是ID3的改进版，为解决ID3偏好多取值特征的问题，引入信息增益率作为分裂准则，即信息增益与特征自身熵的比值。

2. 关键计算步骤

（1）计算特征自身熵

以"天气"特征为例，其自身熵（描述特征取值的不确定性）：

H_{天气} = -\\frac{5}{14}log_2\\frac{5}{14} - \\frac{4}{14}log_2\\frac{4}{14} - \\frac{5}{14}log_2\\frac{5}{14}≈1.577

（2）计算信息增益率

信息增益率公式：$$增益率 = 信息增益 / 特征自身熵$$

天气特征的增益率：$$\frac{0.247}{1.577}≈0.156$$

（3）选择最优特征

所有特征的增益率排序：

天气（0.1566）> 湿度（0.151）> 有风（0.049）> 温度（0.0186）

3. 核心改进与优缺点

🔧 改进：支持连续值特征（通过离散化处理）、处理缺失值、可剪枝防过拟合。
✅ 优点：解决ID3的特征偏好问题，泛化能力更强。
❌ 缺点：计算量更大（需额外计算特征熵），不适合大规模数据。

四、CART决策树：基于基尼系数的二分分裂

1、CART算法核心原理

CART（Classification And Regression Tree）是二叉决策树 ，分类树采用基尼系数选择最优特征与划分点：

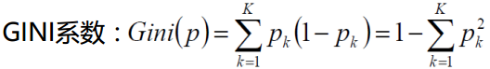
特征的基尼指数：$$Gini(D,A) = \frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2)$$
选择基尼指数最小的特征与划分点作为最优分裂。

2、数据集

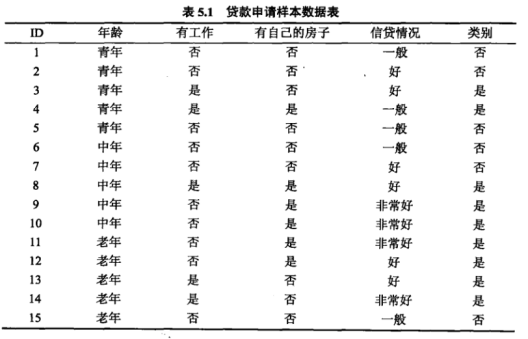
3、计算各特征的基尼指数

以贷款申请数据为例（特征：有自己的房子；标签：是否贷款）：

样本总数15，其中有房6人（全贷款），无房9人（4人贷款）
有房子节点的基尼系数：$$2×\frac{6}{6}×(1-\frac{6}{6})=0$$
无房子节点的基尼系数：$$2×\frac{4}{9}×(1-\frac{4}{9})≈0.49$$
该特征的加权基尼系数：$$\frac{6}{15}×0 + \frac{9}{15}×0.494≈0.29$$

4、最终CART决策树结构

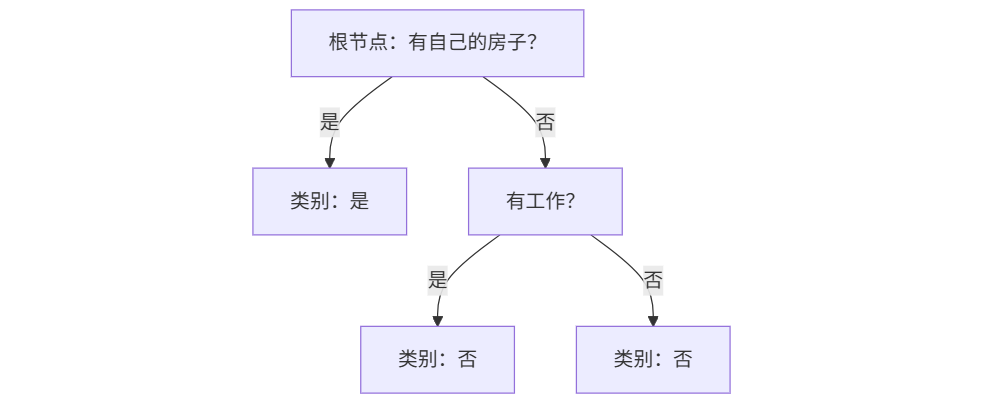
5. 算法特点与优缺点

🔧 核心特点：采用二分分裂（无论特征取值多少，均分成两个子节点），支持连续值和缺失值。
✅ 优点：计算高效（无需对数运算），泛化能力强，可通过剪枝进一步优化。
❌ 缺点：对异常值敏感，在复杂数据上可能需要更多节点才能达到理想效果。

五、三大算法核心对比表

算法	分裂准则	支持特征类型	适用场景	核心优缺点
ID3	信息增益	离散值	简单数据集、快速原型	优点：计算快；缺点：偏好多取值特征
C4.5	信息增益率	离散值、连续值	中小型数据集、需防过拟合	优点：修正偏好，支持多场景；缺点：计算量大
CART	基尼系数	离散值、连续值	大规模数据、分类/回归	优点：高效通用；缺点：对异常值敏感

六、决策树剪枝：避免过拟合的关键步骤

无论哪种算法，生成的决策树都可能出现"过拟合"（对训练数据贴合过好，泛化能力差），因此需要剪枝优化：

预剪枝：生成树时就限制（如限制树深度、最小叶子节点样本数）。
后剪枝：生成完整树后，移除对泛化无帮助的分支。

剪枝的核心目标是在"训练精度"和"泛化能力"之间找到平衡，让决策树在新数据上表现更稳定。