在之前我们学习了KNN算法和线性回归算法,而实际场景中更多的是分类问题(比如判断是否患病、邮件是否为垃圾邮件),今天就来学习更加高级的分类算法 ------ 逻辑回归(Logistic Regression)。
逻辑回归虽然名字里带 "回归",但本质是分类算法,它是线性回归的 "升级版",继承了线性回归简单易懂的特点,又能解决二分类(是 / 否)甚至多分类问题,是工业界应用最广泛的基础算法之一
1.什么是逻辑回归?
逻辑回归就是先通过线性回归的方式计算特征的线性组合,再通过sigmoid 函数将线性结果映射到 0~1 之间,最终以概率形式输出样本属于某一类别的可能性。
举个例子:预测是否患糖尿病时,我们收集 "血糖值、BMI、年龄" 等特征,先用线性组合计算一个分值,再通过 sigmoid 函数把分值转换成 "患病概率"(比如 0.85),若概率≥0.5 则判定为 "患病",否则为 "未患病",这个过程就是逻辑回归。
2.逻辑回归公式(二分类)
2.1 线性组合
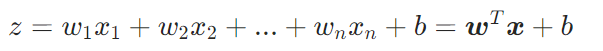
:特征的线性得分(无边界)
:多个输入特征(如血糖、BMI)
:特征对应的权重参数
:偏置参数
2.2sigmoid 函数
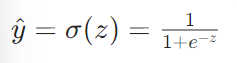
:模型预测概率(0 ≤ y^ ≤ 1),表示样本属于正类(如患病)的概率
:sigmoid 函数,形状为 "S 型曲线",能把任意实数映射到 0~1 区间
2.2.1sigmoid 函数的特点:
当 z=0 时,σ(0)=0.5(分类阈值)
当 z→+∞ 时,σ(z)→1(极大概率属于正类)
当 z→−∞ 时,σ(z)→0(极大概率属于负类)
3.逻辑回归到底在 "找什么"?
逻辑回归的目标和线性回归不同:它不是找 "最小误差的直线",而是找一组最优的参数 w 和 b,让模型输出的概率能最大程度匹配样本的真实类别(0 或 1)。
3.1 损失函数
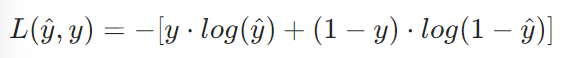
:真实标签(0 或 1)
:预测概率
对于 m 个样本的整体损失:
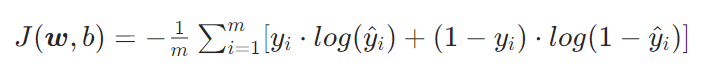
3.2 损失函数的意义:
当真实标签 y=1 时,损失简化为 −log( y ^ ) : y ^ 越接近 1,损失越小; y ^ 接近 0,损失趋近于无穷大
当真实标签 y=0 时,损失简化为 −log(1− y ^ ) : y ^ 越接近 0,损失越小; y ^ 接近 1,损失趋近于无穷大
整体损失是凸函数,只有一个最小值点,可通过梯度下降找到最优参数
3.3 梯度下降法
逻辑回归没有像线性回归那样的解析解,需要通过梯度下降迭代求解最优参数:
1.初始化参数 和
(通常为 0)
2.计算每个参数的梯度(损失函数对参数的偏导数)
3.沿梯度负方向更新参数:,
(
为学习率)
4.重复步骤 2-3,直到损失收敛或达到最大迭代次数
4.逻辑回归项目实战
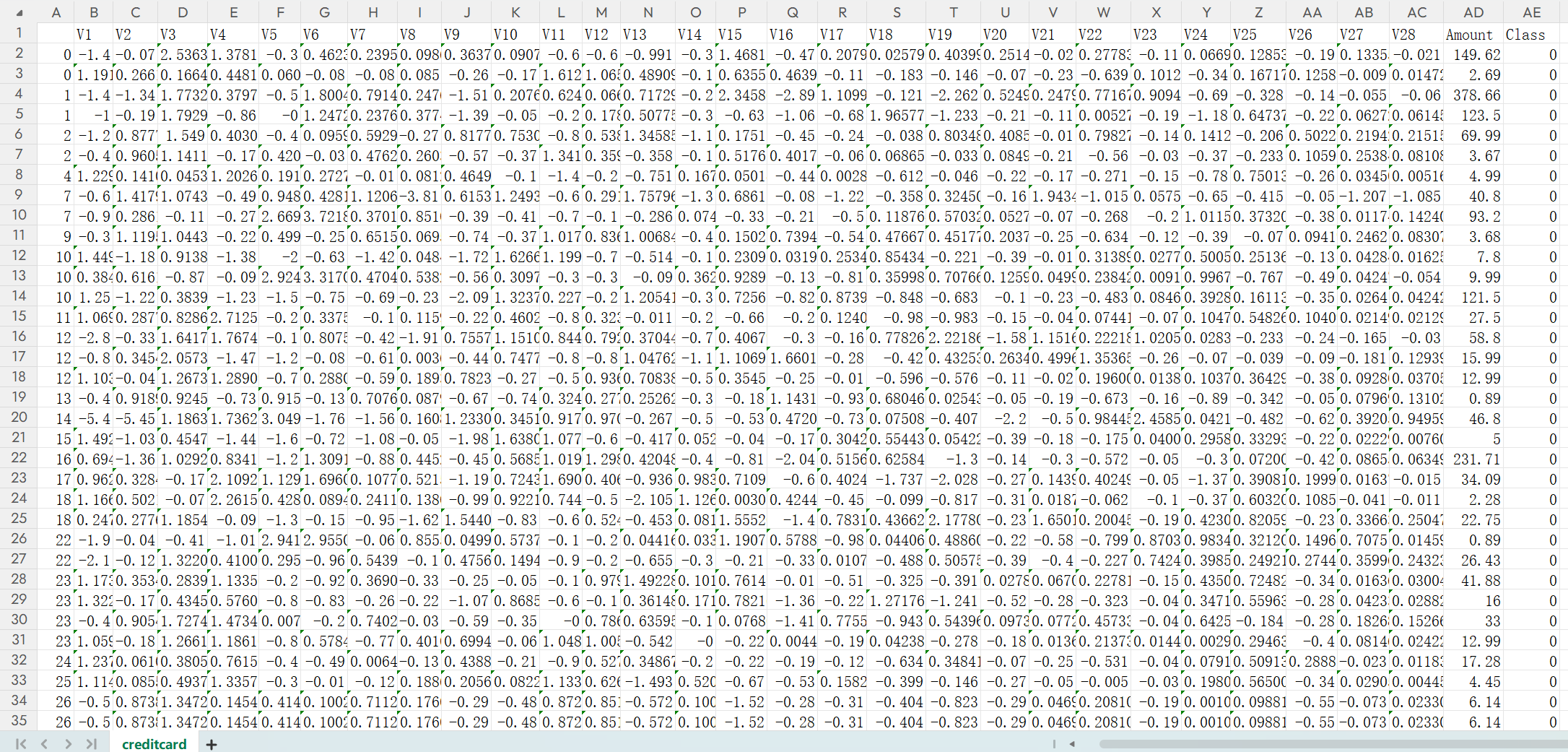
这个是某省银行的信用卡数据,数据已经脱敏,其中Amount没有标准化需要Z标准化,Class是是否违约,违约就是1,没有就是0(有需要的大学生可以直接下载数据集拿去用,互帮互助嘛)
import pandas as pd
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from pylab import mpl
from sklearn.model_selection import train_test_split
from sklearn import metrics
from sklearn.linear_model import LogisticRegression
data = pd.read_csv("creditcard.csv")
scaler = StandardScaler()
data['Amount'] = scaler.fit_transform(data[['Amount']])
data = data.drop(['Time'], axis=1)
mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']
mpl.rcParams['axes.unicode_minus'] = False
labels_count = data['Class'].value_counts()
print("正负例样本数量:")
print(labels_count)
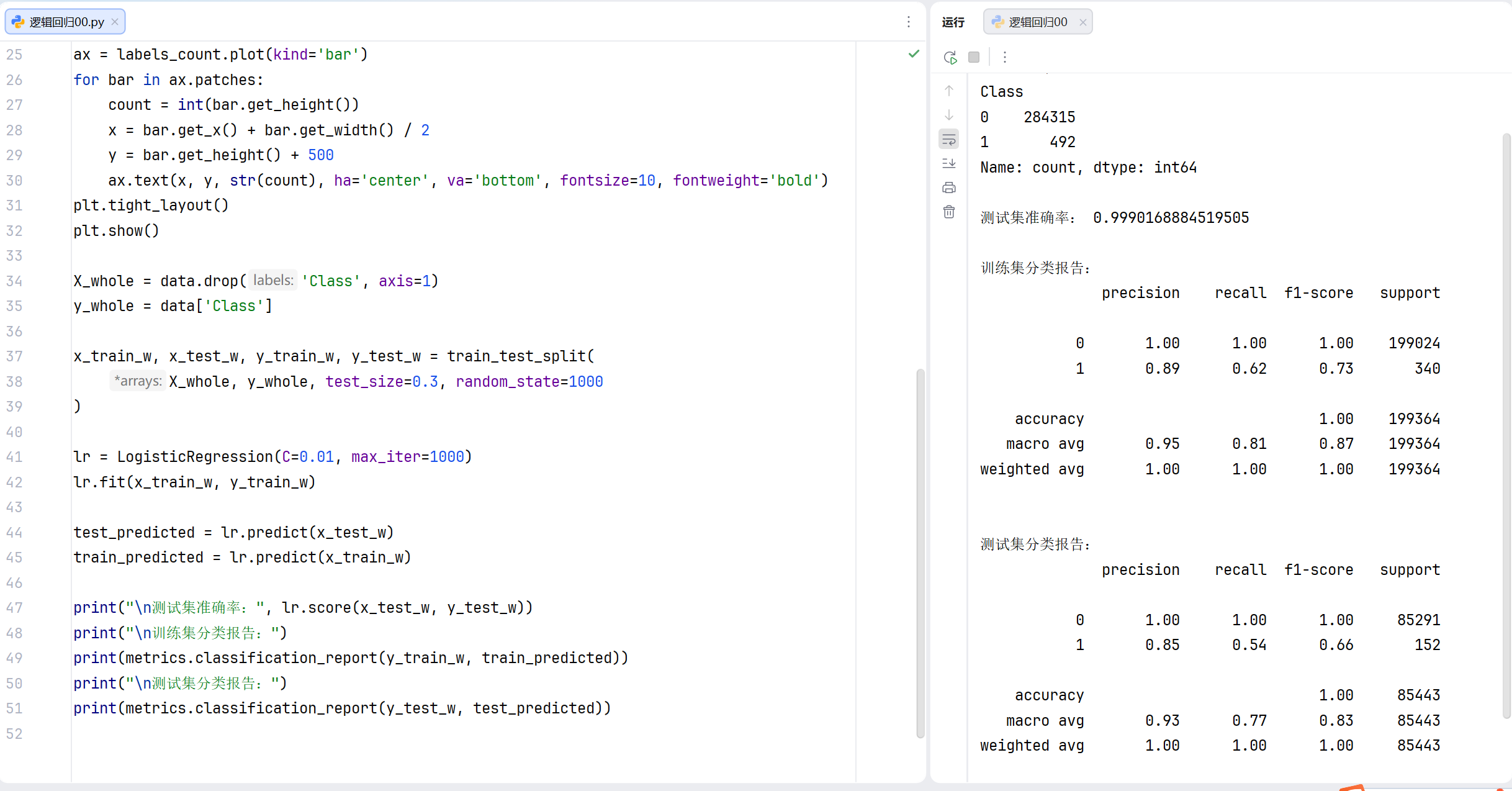
plt.title("正负例样本数")
plt.xlabel("类别")
plt.ylabel("频数")
labels_count.plot(kind='bar')
plt.show()
X_whole = data.drop('Class', axis=1)
y_whole = data['Class']
x_train_w, x_test_w, y_train_w, y_test_w = train_test_split(
X_whole, y_whole, test_size=0.3, random_state=1000
)
lr = LogisticRegression(C=0.01, max_iter=1000)
lr.fit(x_train_w, y_train_w)
test_predicted = lr.predict(x_test_w)
train_predicted = lr.predict(x_train_w)
print("\n测试集准确率:", lr.score(x_test_w, y_test_w))
print("\n训练集分类报告:")
print(metrics.classification_report(y_train_w, train_predicted))
print("\n测试集分类报告:")
print(metrics.classification_report(y_test_w, test_predicted))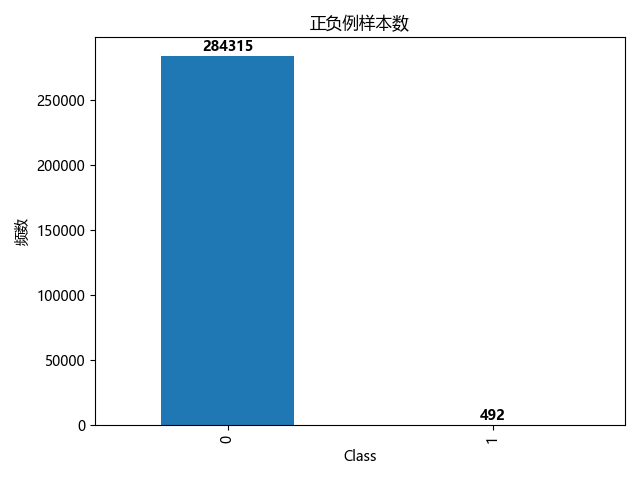
5.代码详解
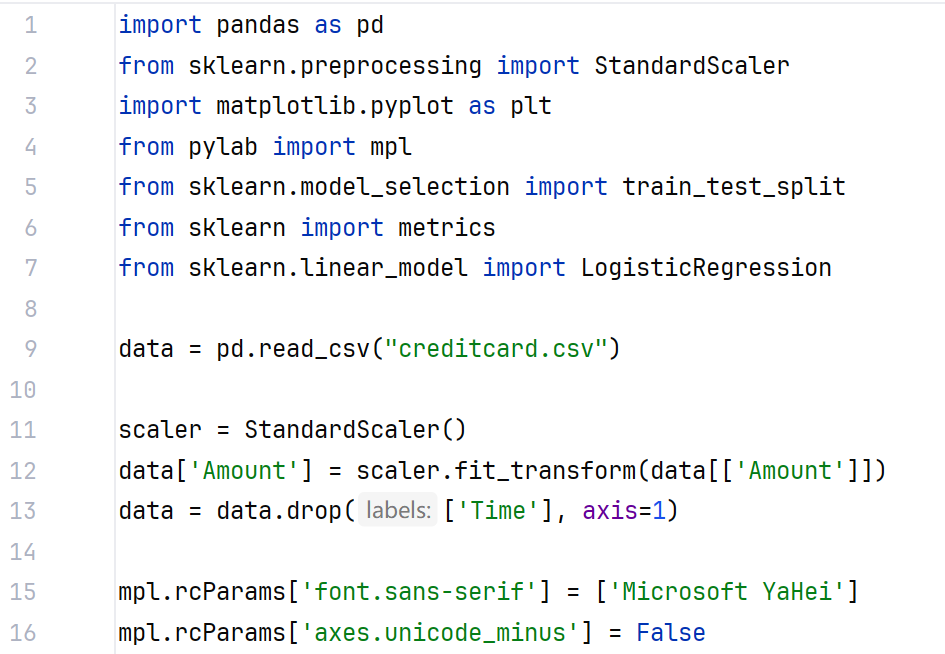
导入必要库和数据,然后对数据进行预处理,其中对Amount进行Z标准化,再将Time一列删除。然后再设置字体是微软雅黑

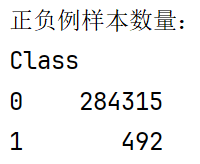
显示正负样本数量


输出一个柱状图展示数据。

将'Class'列作为y标签,其他列作为x标签

将30% 的数据作为测试集,70% 作为训练集。
使用random_state=1000固定随机种子,保证每次运行划分结果一致,便于复现。

设置C=0.01值越小表示正则化越强,用来防止模型过拟合。(后期可以调整参数来优化模型) max_iter=1000:设置最大迭代次数为 1000,确保模型能收敛。

用训练好的模型进行预测并打印结果
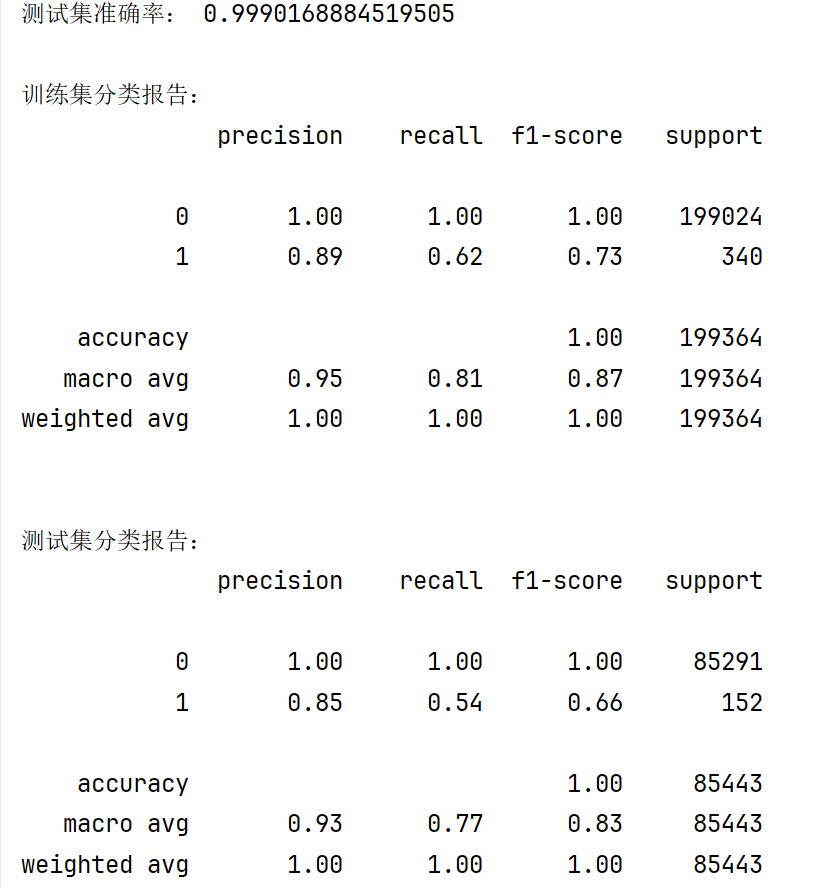
以上就是逻辑回归的第一部分,明天会介绍第二部分如何提高模型的准确率
日记
2月5日,星期四
睡过头了
今天周四是自习,结果闹钟没醒,11点才醒,看了一眼wx
你们以为道歉的是我,no,no,no,我当时还没醒。也算是午饭前赶到教室自习了。说是3个,但是还有一个高手好像晚上才到,也许是请假了,未知全貌就不要在背后恶意猜测。