目录
[4.1 初始化](#4.1 初始化)
[4.2 PSO速度更新](#4.2 PSO速度更新)
[4.3 PSO位置更新](#4.3 PSO位置更新)
[4.4 适应度函数设计](#4.4 适应度函数设计)
本文研究了基于粒子群优化(PSO)算法的无刷直流电机PI控制器参数优化方法。PSO算法通过模拟鸟群觅食行为,无需目标函数梯度信息即可实现全局优化,具有参数少、收敛快的特点。研究建立了包含速度更新、位置更新机制的PSO优化模型,设计了基于ITAE误差积分指标的适应度函数,综合评估系统动态和稳态性能。Matlab仿真结果表明,该方法能有效优化Kp、Ki参数,实现电机调速控制的多目标优化。完整工程文件可通过指定关键词获取,为相关领域研究提供了实用参考。
1.课题概述
粒子群优化(PSO)作为群体智能优化算法,无需目标函数连续可导、无需梯度信息,具备全局搜索能力强、收敛速度较快、参数少、易编程实现等特点,可在线/离线优化PI控制器的比例系数Kp与积分系数Ki,使控制系统在多目标约束(超调量、调节时间、稳态误差、抗扰性)下达到最优动态/稳态性能,实现无刷直流电机的最优调速控制。
2.系统仿真结果
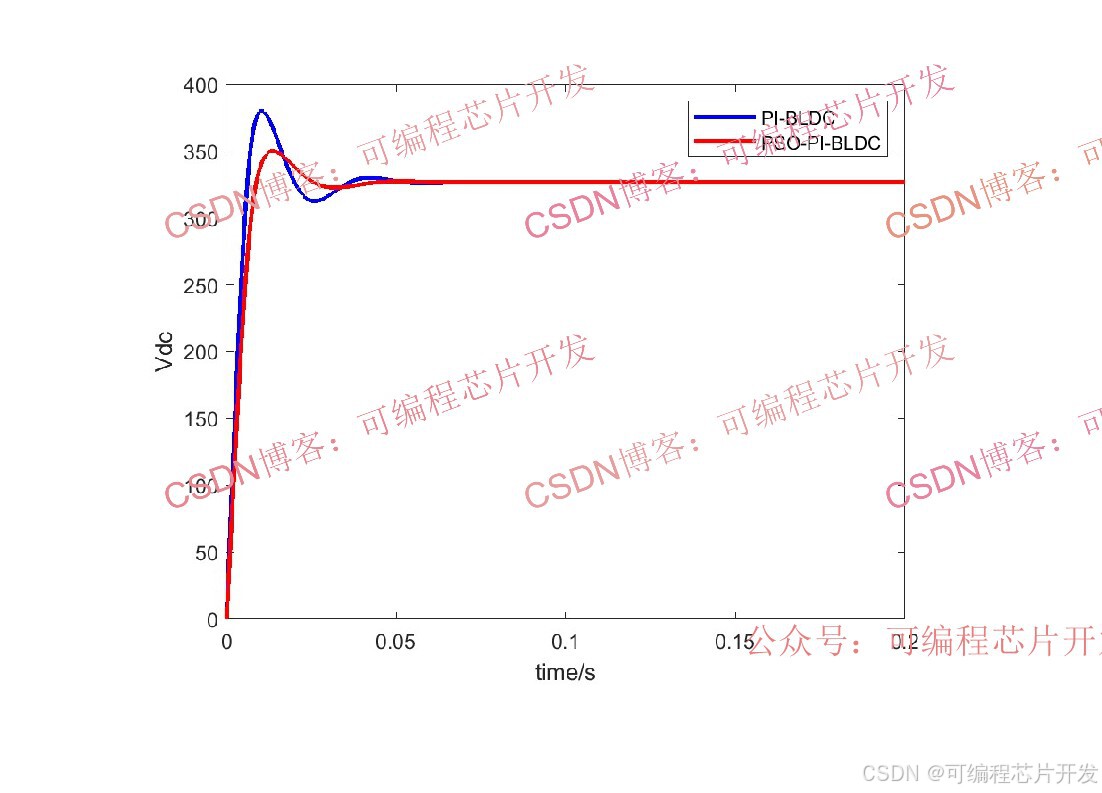
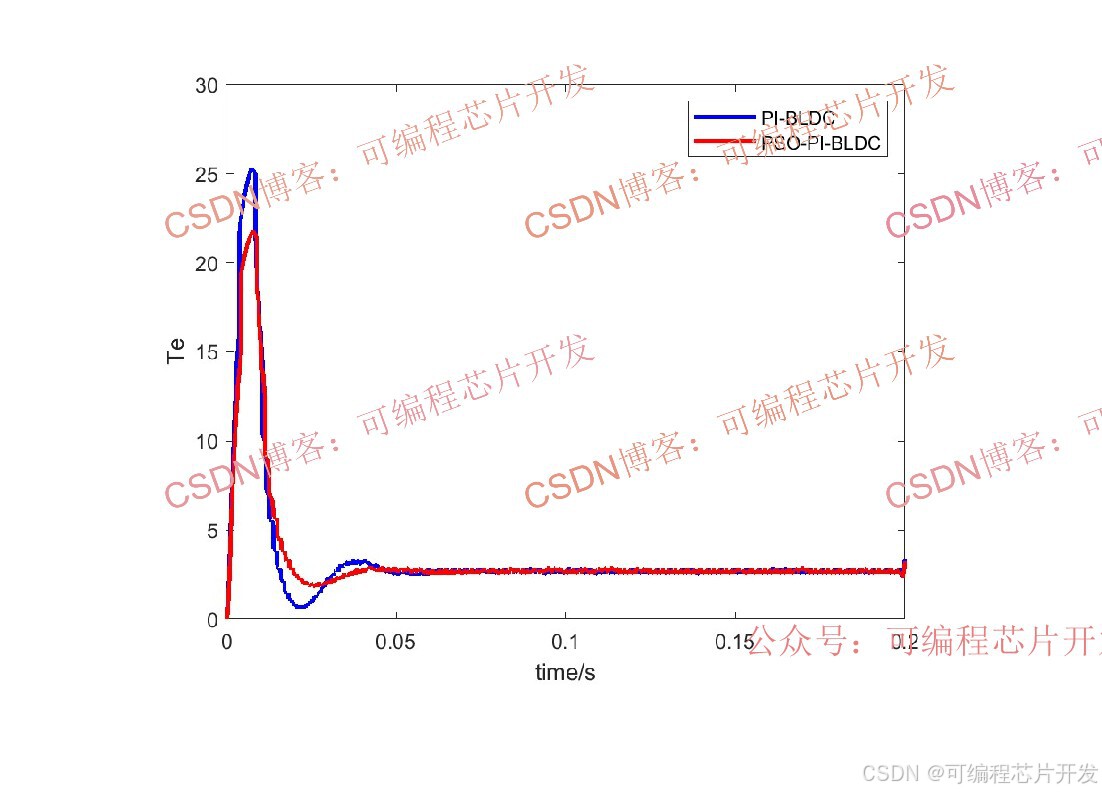
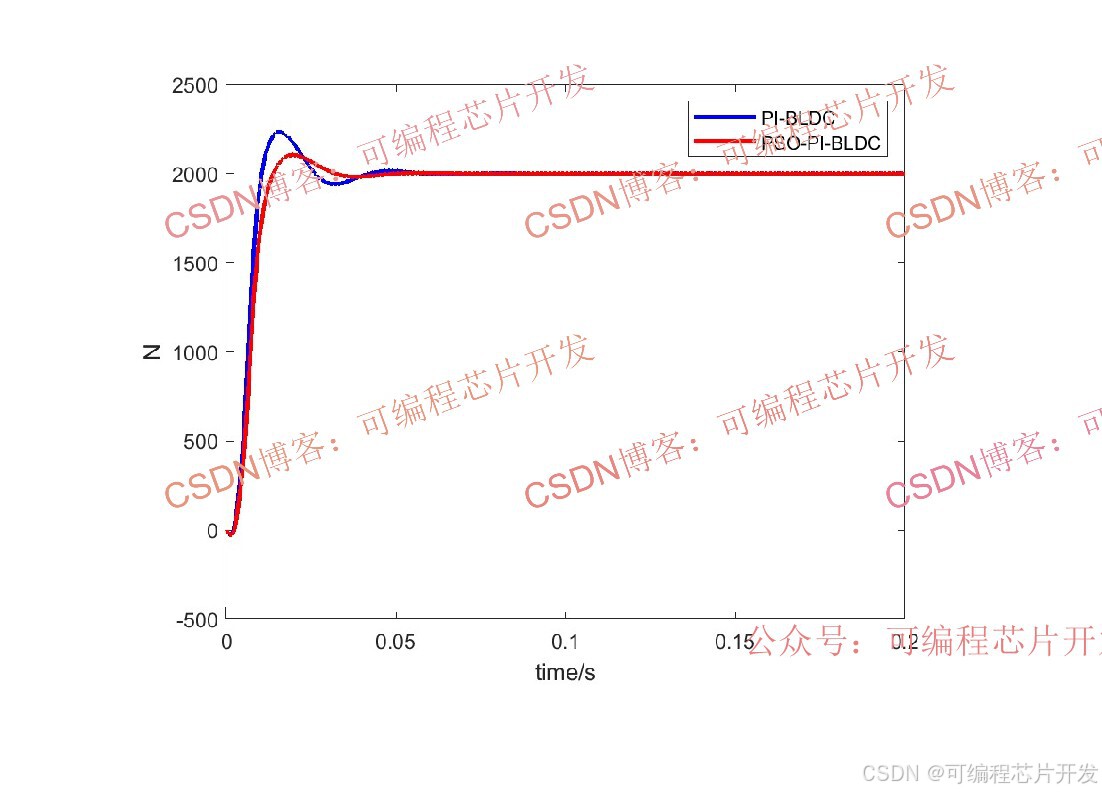
3.核心程序或模型
版本:Matlab2024b
.....................................................
for i=1:Iter
i
for j=1:Npop
[i,j]
Kp = x1(j,1);
Ki = x1(j,2);
sim('tops1_fit.slx');
%导入simulink仿真输出,计算适应度值
load Ref2.mat
Ref = ans.Data;
load N2.mat
Yout = ans.Data;
yfits = mean((Ref-Yout).^2);
if yfits<pbest1(j)
p1(j,:) = x1(j,:);
pbest1(j) = yfits;
end
if pbest1(j)<gbest1
g1 = p1(j,:);
gbest1 = pbest1(j);
end
v1(j,:) = v1(j,:)+c1*rand*(p1(j,:)-x1(j,:))+c2*rand*(g1-x1(j,:));
x1(j,:) = x1(j,:)+v1(j,:);
for k=1:dims
if x1(j,k) >= tmps(2,k)
x1(j,k) = tmps(2,k);
end
if x1(j,k) <= tmps(1,k)
x1(j,k) = tmps(1,k);
end
end
for k=1:dims
if v1(j,k) >= tmps(2,k)/10
v1(j,k) = tmps(2,k)/10;
end
if v1(j,k) <= tmps(1,k)/10
v1(j,k) = tmps(1,k)/10;
end
end
end
gb1(i)=gbest1;
end
%提取PSO的优化结果
X = g1;
%将变量导入到simulink模型中
Kp=X(1);
Ki=X(2);
sim('tops1_pso.slx');
1444.系统原理简介
PSO由Kennedy与Eberhart于1995年提出,模拟鸟群觅食行为:群体中每个粒子代表优化问题的一个候选解,粒子通过跟踪个体最优位置(自身历史最优解)与全局最优位置(整个群体历史最优解)更新速度与位置,逐步收敛至全局最优解。
4.1 初始化
设优化问题维度为D,本文优化目标为PI参数Ki、kp,故D=2。

4.2 PSO速度更新
粒子速度由惯性分量、个体认知分量、社会学习分量三部分组成,标准PSO速度更新公式:
各参数含义:

4.3 PSO位置更新
粒子速度决定位置变化,位置更新公式:
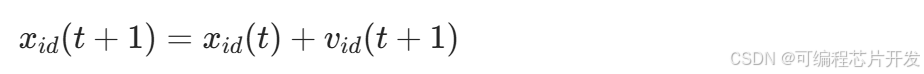
4.4 适应度函数设计
适应度函数是PSO寻优的评价标准,需综合衡量控制系统动态性能、稳态性能、抗扰性能,无刷直流电机调速控制常用误差积分型指标,最常用ITAE(时间乘绝对误差积分),兼顾响应速度、超调与稳态误差,表达式:
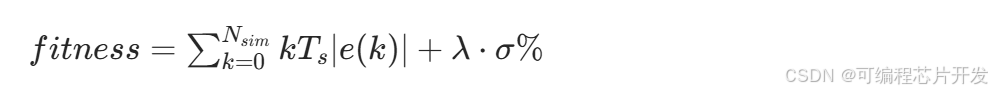
优化目标:最小化适应度函数值,对应控制系统性能最优。
5.完整工程文件
v v
关注后,GZH回复关键词:a26,
或回复关键词:PSOPI