《机器学习导论》第 9 章-决策树

目录

前言

[9.1 引言](#9.1 引言)

[9.2 单变量树](#9.2 单变量树)

[9.2.1 分类树](#9.2.1 分类树)

核心概念通俗解释

[完整可运行代码（分类树 + 可视化对比）](#完整可运行代码（分类树 + 可视化对比）)

代码运行效果说明

[9.2.2 回归树](#9.2.2 回归树)

核心概念通俗解释

[完整可运行代码（回归树 + 可视化对比）](#完整可运行代码（回归树 + 可视化对比）)

代码运行效果说明

[9.3 剪枝](#9.3 剪枝)

核心概念通俗解释

完整可运行代码（剪枝效果对比）

代码运行效果说明

[9.4 由决策树提取规则](#9.4 由决策树提取规则)

完整可运行代码（提取决策树规则）

代码运行效果说明

[9.5 由数据学习规则](#9.5 由数据学习规则)

[9.6 多变量树](#9.6 多变量树)

[完整可运行代码（多变量树 vs 单变量树对比）](#完整可运行代码（多变量树 vs 单变量树对比）)

代码运行效果说明

[9.7 注释](#9.7 注释)

[9.8 习题](#9.8 习题)

[9.9 参考文献](#9.9 参考文献)

总结

---

前言

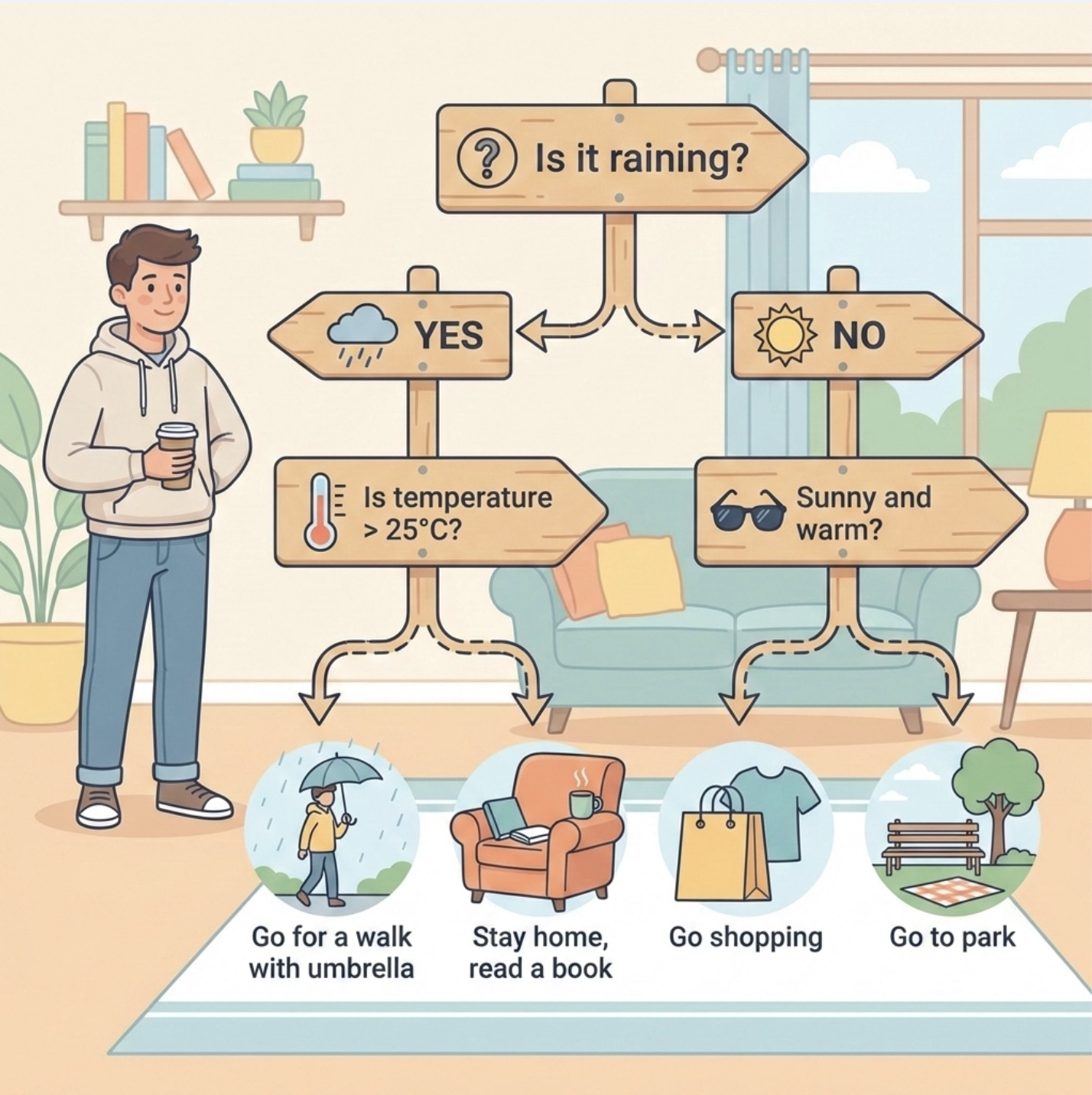
决策树是机器学习中最 "接地气" 的算法之一 ------ 它就像我们日常生活中 "层层追问做选择" 的过程：比如周末要不要出门，先看 "是否下雨"，再看 "温度是否超过 25℃"，最后决定 "出门逛街" 还是 "宅家追剧"。这篇文章结合《机器学习导论》第 9 章内容，用通俗易懂的语言拆解决策树核心知识点，搭配完整可运行的 Python 代码 和直观的可视化对比图，帮你彻底搞懂决策树从原理到落地的全过程。

---

9.1 引言

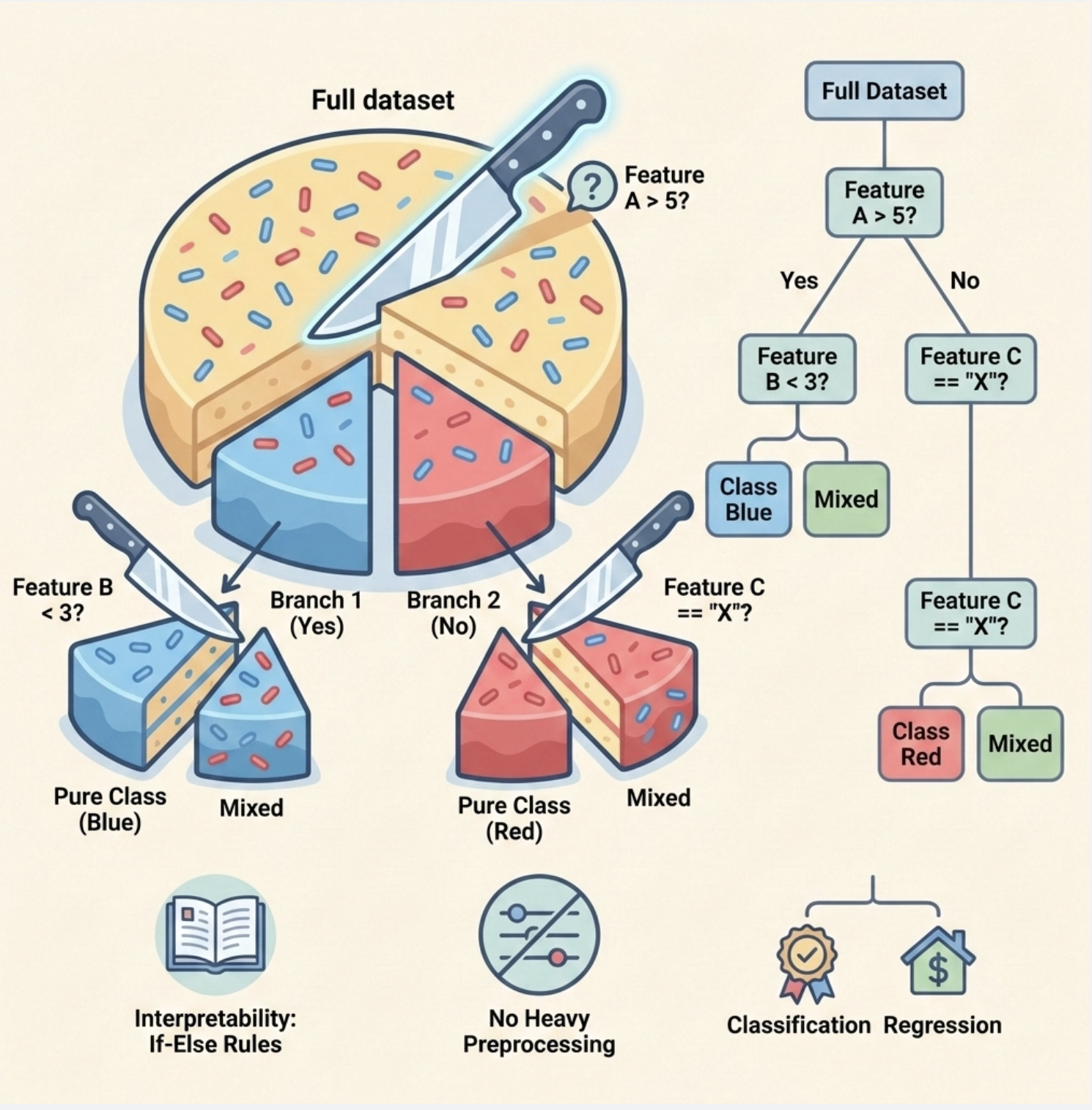
决策树本质是一种 "分而治之" 的贪心算法：把复杂的数据集像切蛋糕一样，按某个特征一步步切分，直到每个小块足够 "纯粹"（比如分类任务中，小块里全是同一类样本）。

它的核心优势：

• 直观易懂，生成的决策规则像 "if-else" 一样好解释；
• 不需要复杂的特征预处理（比如归一化）；
• 既能解决分类问题（比如判断邮件是否为垃圾邮件），也能解决回归问题（比如预测房价）。

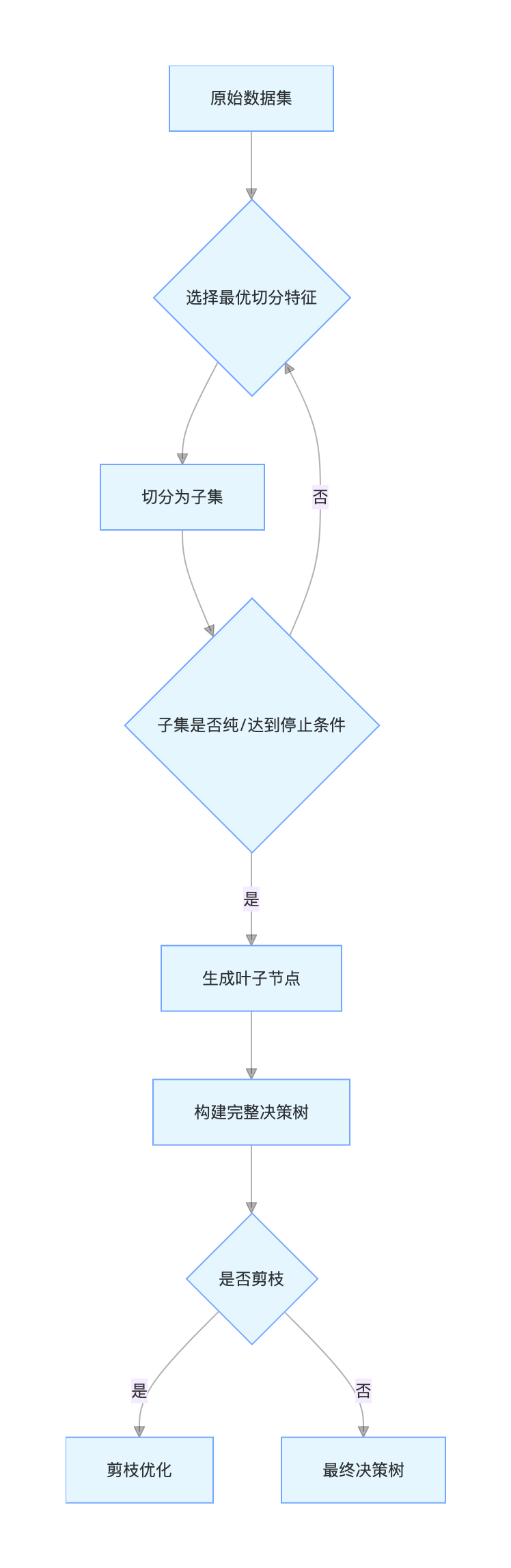
画个决策树的核心逻辑流程图：

---

9.2 单变量树

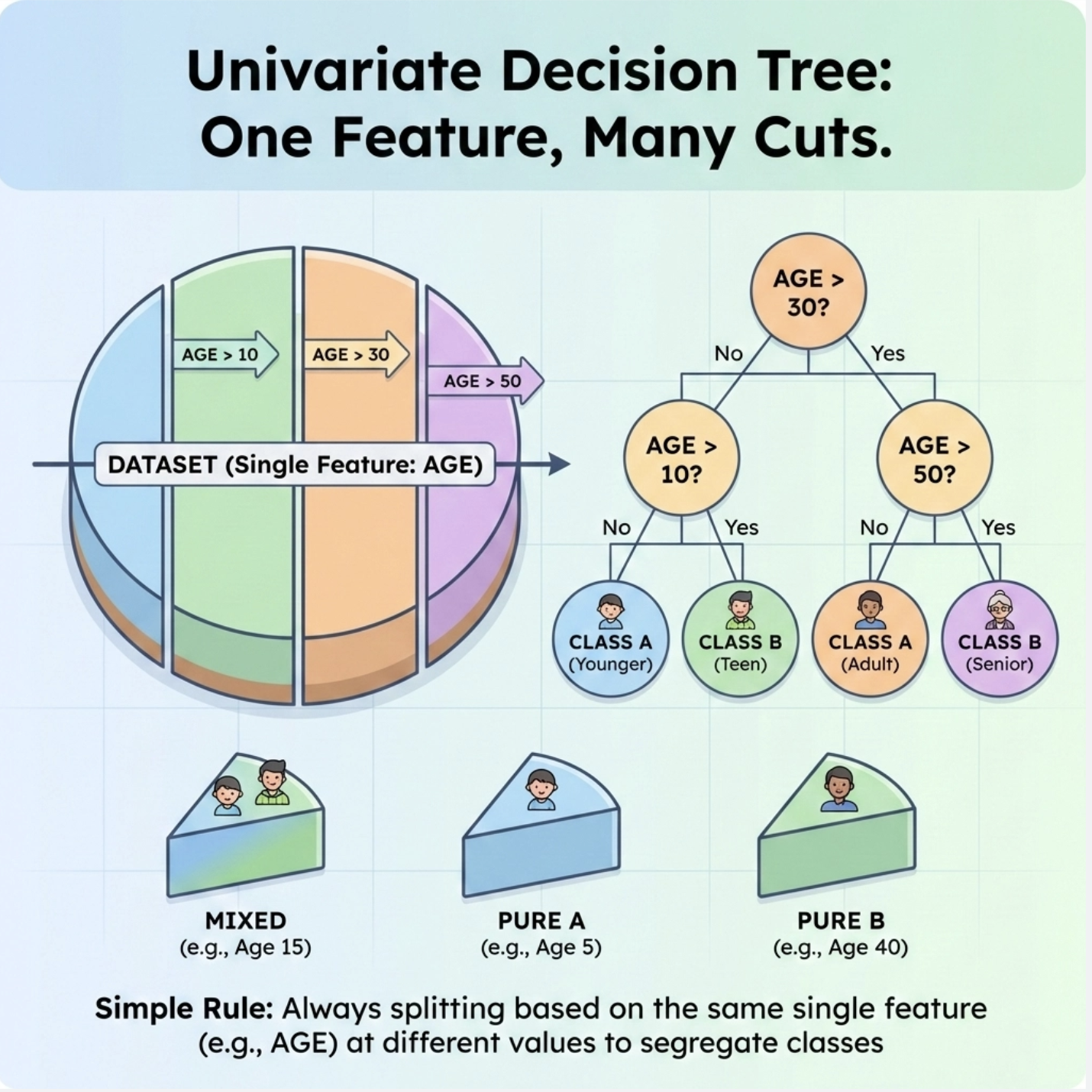
单变量树是最基础的决策树 ------ 每次切分只基于一个特征（比如只看 "年龄" 或只看 "收入"），这也是我们入门最容易理解的版本。

9.2.1 分类树

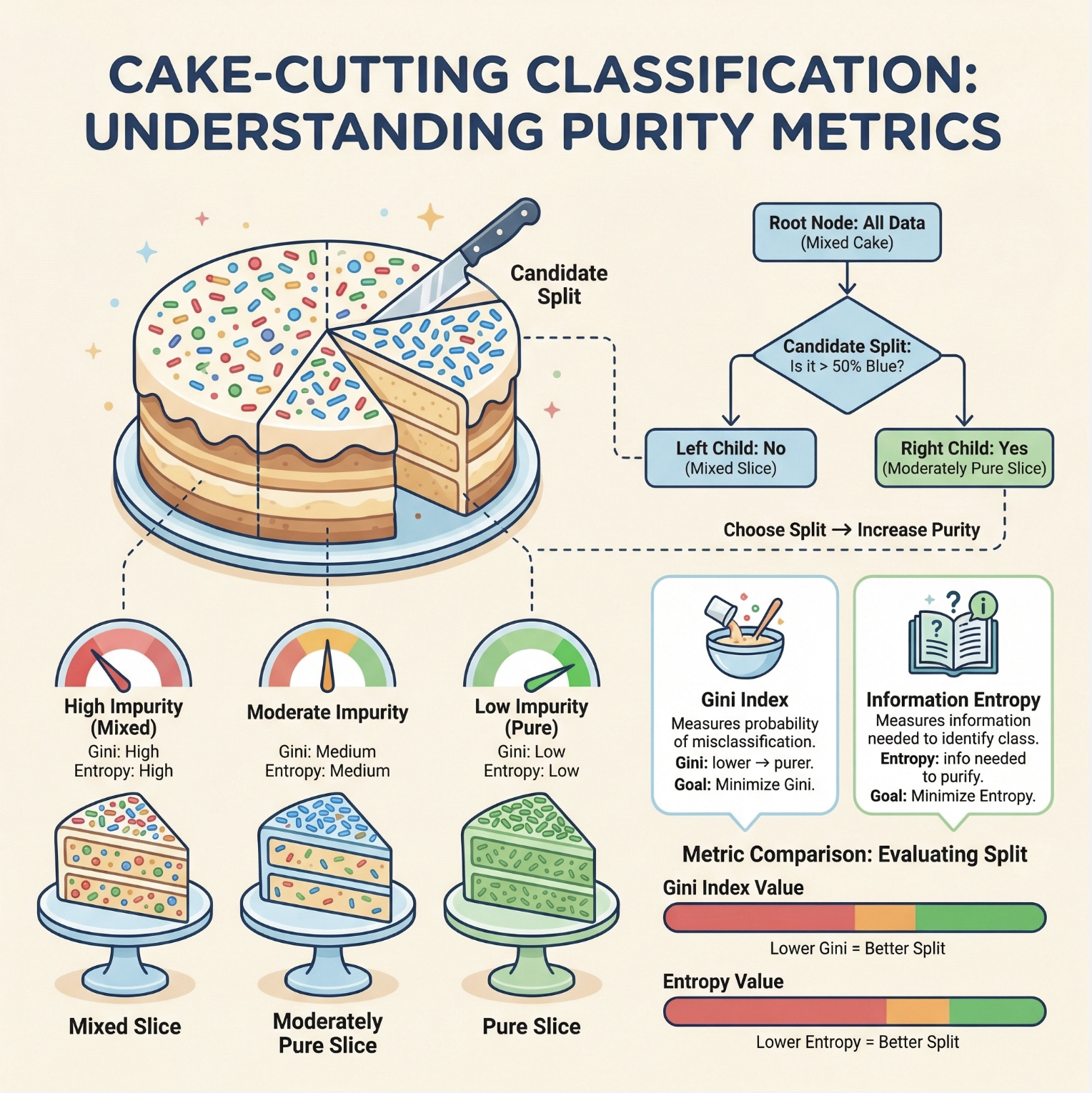
分类树用于解决离散标签 的分类问题（比如判断鸢尾花品种、判断客户是否流失），核心是通过 "纯度指标"（比如基尼系数、信息熵）选择最优切分特征，让切分后的子集尽可能 "纯"。

核心概念通俗解释

基尼系数 ：衡量样本的 "混乱程度"，数值越小越纯（0 表示子集全是同一类，1 表示最混乱）；

信息熵 ：和基尼系数作用类似，也是衡量混乱程度（可以理解为 "要搞清楚这个子集需要多少信息量"）。

完整可运行代码（分类树 + 可视化对比）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# ====================== Mac系统Matplotlib中文显示配置 ======================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# ====================== 1. 加载数据并预处理 ======================
# 加载经典的鸢尾花数据集（分类任务）
iris = load_iris()
X = iris.data[:, :2]  # 简化：只取前两个特征（花萼长度、花萼宽度），方便可视化
y = iris.target
feature_names = ['花萼长度(cm)', '花萼宽度(cm)']
class_names = iris.target_names

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ====================== 2. 训练不同参数的分类决策树 ======================
# 模型1：深度为2的决策树（浅树，防止过拟合）
tree_depth2 = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_depth2.fit(X_train, y_train)

# 模型2：无深度限制的决策树（深树，容易过拟合）
tree_nolimit = DecisionTreeClassifier(random_state=42)
tree_nolimit.fit(X_train, y_train)

# ====================== 3. 模型评估 ======================
y_pred_depth2 = tree_depth2.predict(X_test)
y_pred_nolimit = tree_nolimit.predict(X_test)

acc_depth2 = accuracy_score(y_test, y_pred_depth2)
acc_nolimit = accuracy_score(y_test, y_pred_nolimit)

print(f"深度为2的决策树测试集准确率：{acc_depth2:.2f}")
print(f"无深度限制的决策树测试集准确率：{acc_nolimit:.2f}")

# ====================== 4. 可视化对比（决策边界+树结构） ======================
# 定义绘制决策边界的函数
def plot_decision_boundary(clf, X, y, title, ax):
    # 生成网格点
    h = 0.02  # 网格步长
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))
    
    # 预测网格点类别
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    
    # 绘制决策边界
    ax.contourf(xx, yy, Z, alpha=0.75, cmap=plt.cm.RdYlBu)
    # 绘制样本点
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap=plt.cm.RdYlBu)
    ax.set_xlabel(feature_names[0])
    ax.set_ylabel(feature_names[1])
    ax.set_title(title)
    ax.legend(*scatter.legend_elements(), title="类别")

# 创建2行1列的子图，对比不同深度的决策树
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 12))

# 绘制深度为2的决策边界
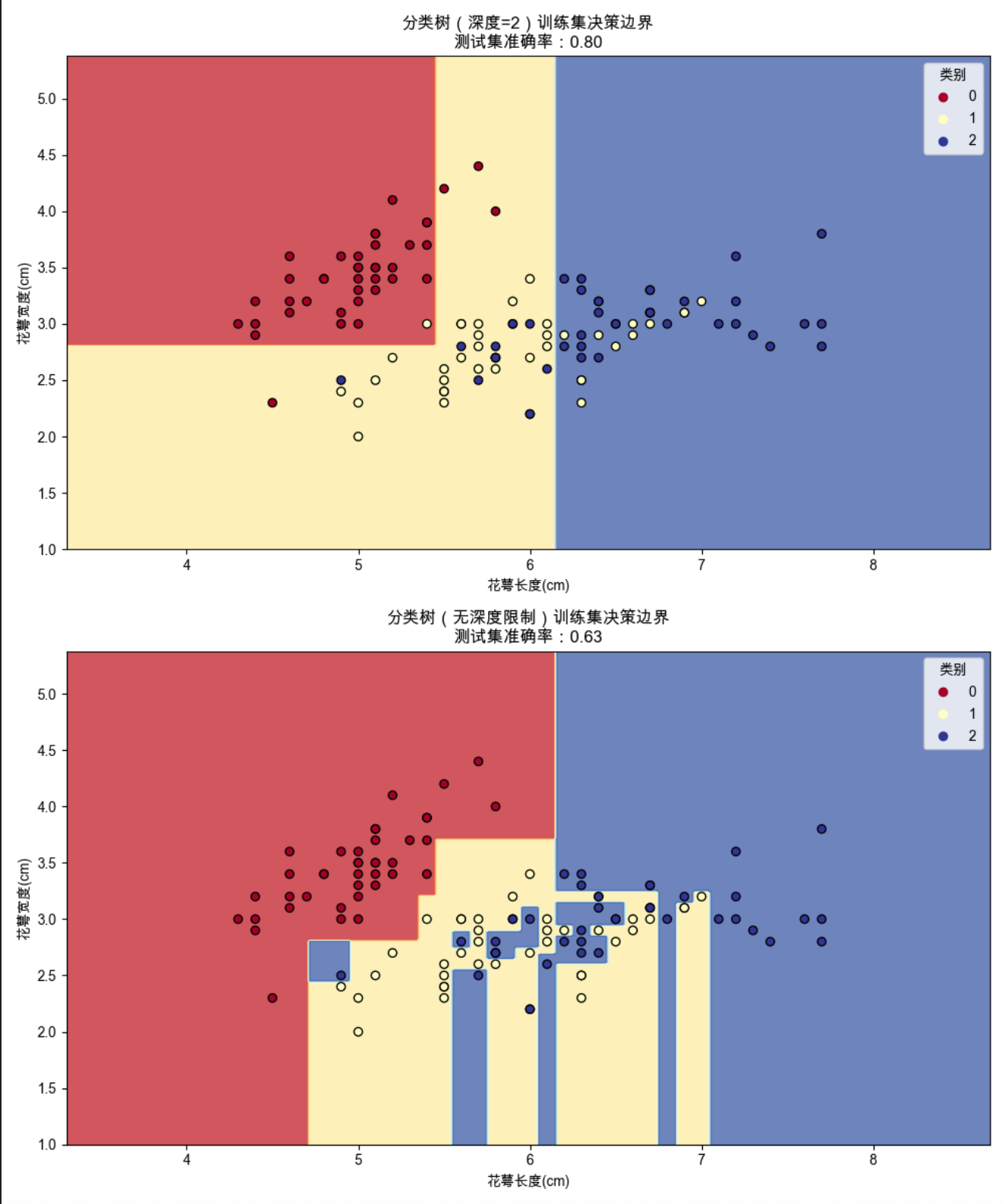
plot_decision_boundary(tree_depth2, X_train, y_train, 
                       f"分类树（深度=2）训练集决策边界\n测试集准确率：{acc_depth2:.2f}", ax1)

# 绘制无深度限制的决策边界
plot_decision_boundary(tree_nolimit, X_train, y_train, 
                       f"分类树（无深度限制）训练集决策边界\n测试集准确率：{acc_nolimit:.2f}", ax2)

plt.tight_layout()
plt.show()

# 可视化深度为2的决策树结构（更易理解）
plt.figure(figsize=(10, 6))
plot_tree(tree_depth2, feature_names=feature_names, class_names=class_names, 
          filled=True, rounded=True, fontsize=10)
plt.title("分类决策树结构（深度=2）")
plt.show()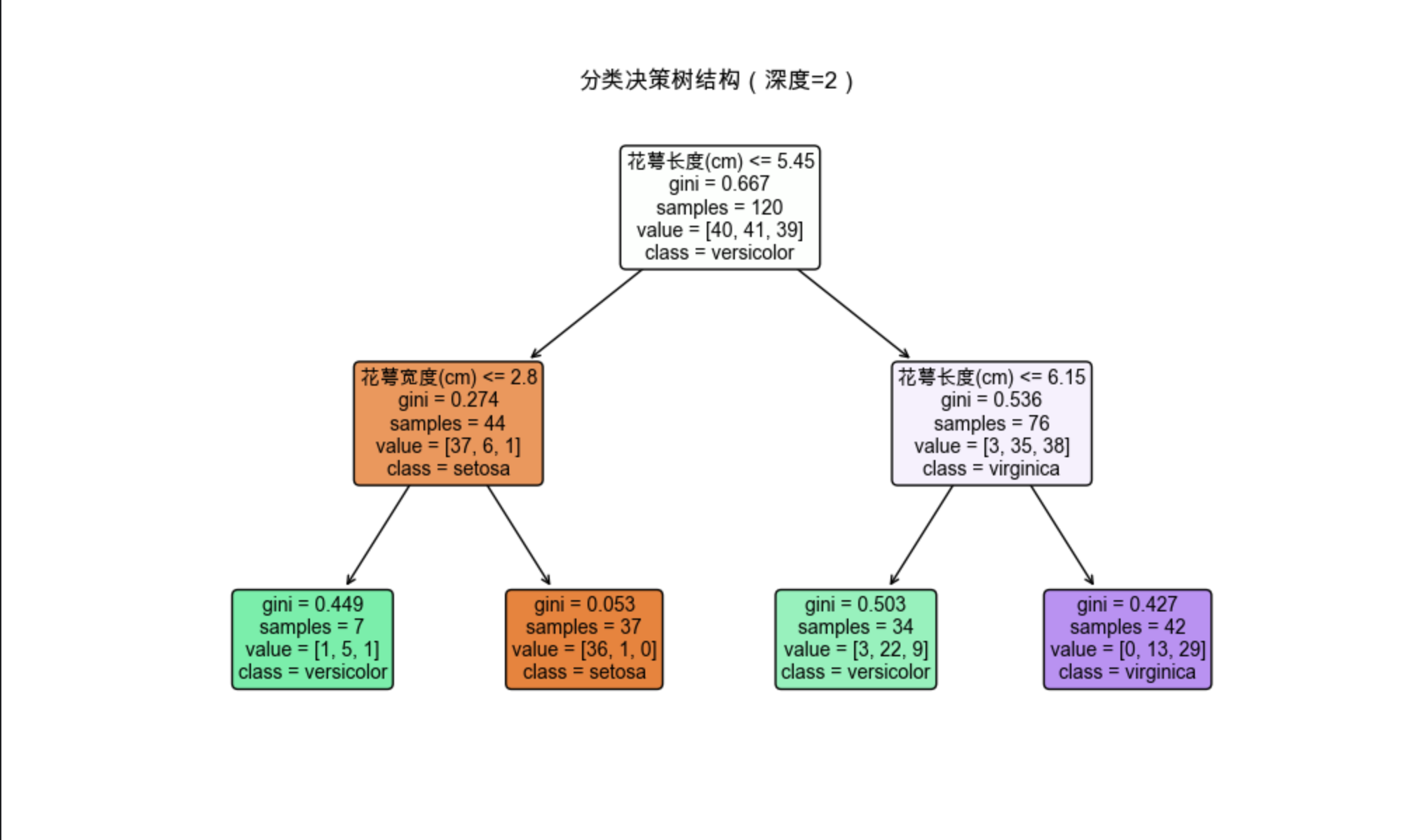

代码运行效果说明

1.会输出两个模型的测试集准确率（通常深度为 2 的模型泛化性更好，无限制的模型容易过拟合）；

2.第一个图是决策边界对比：浅树的边界更简单，深树的边界更复杂（甚至拟合了噪声）；

3.第二个图是决策树的结构可视化，能清晰看到 "根节点→内部节点→叶子节点" 的切分逻辑。

9.2.2 回归树

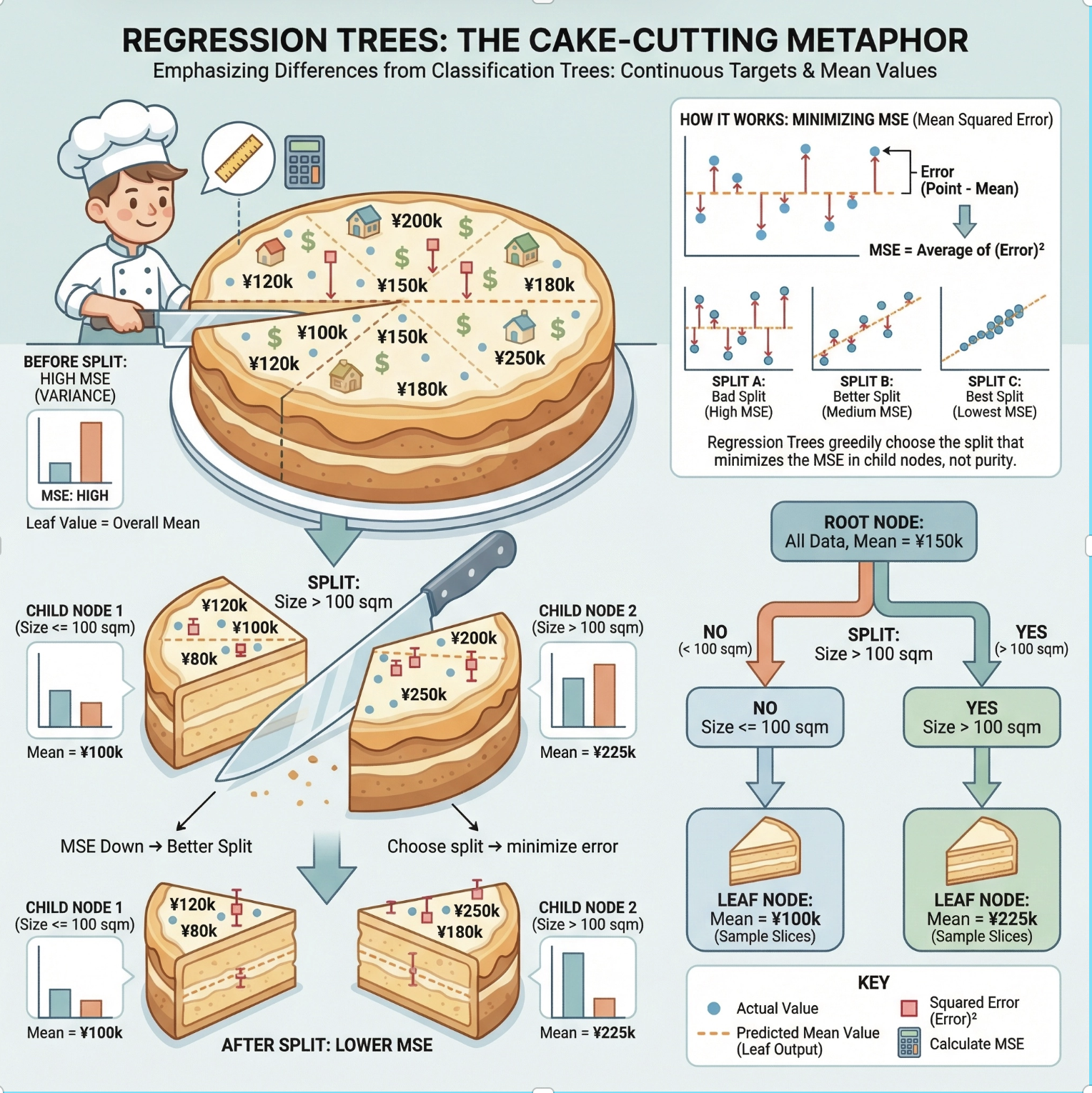
回归树用于解决连续值 的回归问题（比如预测房价、预测销量），核心区别是：分类树用 "纯度" 选特征，回归树用 "误差"（比如均方误差 MSE）选特征，目标是让切分后的子集内样本的预测值尽可能接近真实值。

核心概念通俗解释

均方误差（MSE） ：衡量预测值和真实值的差距，回归树切分的目标是让 MSE 最小；

回归树叶节点值：分类树叶节点是 "类别"，回归树叶节点是 "该子集样本的均值"（比如预测房价时，某个叶子节点的输出是该区域所有房子的平均价格）。

完整可运行代码（回归树 + 可视化对比）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# ====================== Mac系统Matplotlib中文显示配置 ======================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# ====================== 1. 生成模拟回归数据 ======================
# 生成带噪声的回归数据（1个特征，方便可视化）
X, y = make_regression(n_samples=200, n_features=1, noise=20, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ====================== 2. 训练不同参数的回归决策树 ======================
# 模型1：深度为2的回归树（欠拟合倾向）
tree_reg_depth2 = DecisionTreeRegressor(max_depth=2, random_state=42)
tree_reg_depth2.fit(X_train, y_train)

# 模型2：深度为5的回归树（拟合更好）
tree_reg_depth5 = DecisionTreeRegressor(max_depth=5, random_state=42)
tree_reg_depth5.fit(X_train, y_train)

# 模型3：无深度限制的回归树（过拟合倾向）
tree_reg_nolimit = DecisionTreeRegressor(random_state=42)
tree_reg_nolimit.fit(X_train, y_train)

# ====================== 3. 模型评估 ======================
y_pred_depth2 = tree_reg_depth2.predict(X_test)
y_pred_depth5 = tree_reg_depth5.predict(X_test)
y_pred_nolimit = tree_reg_nolimit.predict(X_test)

mse_depth2 = mean_squared_error(y_test, y_pred_depth2)
mse_depth5 = mean_squared_error(y_test, y_pred_depth5)
mse_nolimit = mean_squared_error(y_test, y_pred_nolimit)

print(f"深度=2的回归树MSE：{mse_depth2:.2f}")
print(f"深度=5的回归树MSE：{mse_depth5:.2f}")
print(f"无深度限制的回归树MSE：{mse_nolimit:.2f}")

# ====================== 4. 可视化对比（拟合曲线） ======================
# 生成密集的测试点，绘制拟合曲线
X_range = np.linspace(X.min(), X.max(), 100).reshape(-1, 1)
y_pred_depth2_range = tree_reg_depth2.predict(X_range)
y_pred_depth5_range = tree_reg_depth5.predict(X_range)
y_pred_nolimit_range = tree_reg_nolimit.predict(X_range)

plt.figure(figsize=(12, 8))
# 绘制原始数据点
plt.scatter(X_train, y_train, alpha=0.5, label="训练数据", color="blue")
plt.scatter(X_test, y_test, alpha=0.8, label="测试数据", color="red", marker="x")

# 绘制不同模型的拟合曲线
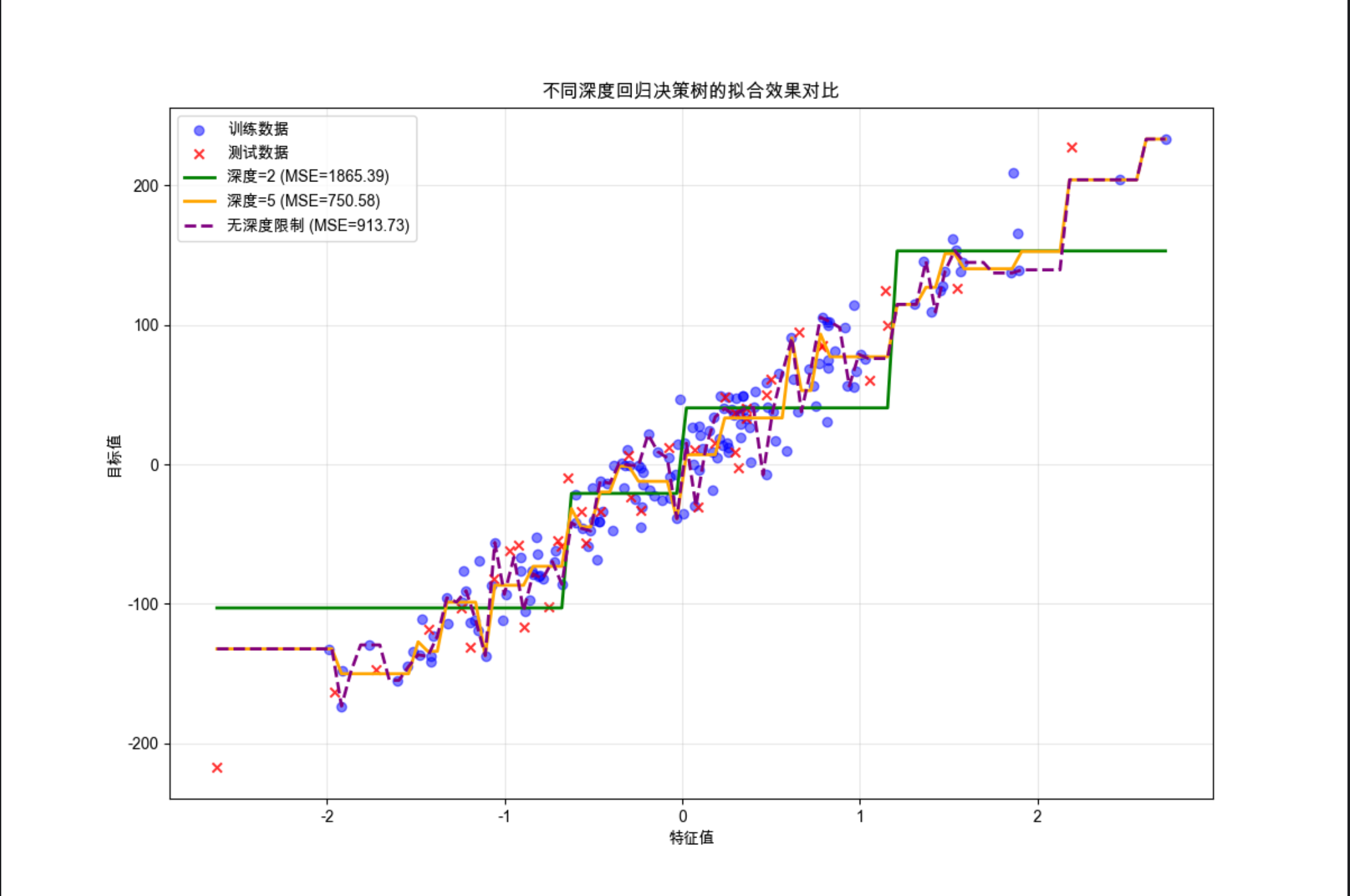
plt.plot(X_range, y_pred_depth2_range, label=f"深度=2 (MSE={mse_depth2:.2f})", linewidth=2, color="green")
plt.plot(X_range, y_pred_depth5_range, label=f"深度=5 (MSE={mse_depth5:.2f})", linewidth=2, color="orange")
plt.plot(X_range, y_pred_nolimit_range, label=f"无深度限制 (MSE={mse_nolimit:.2f})", linewidth=2, color="purple", linestyle="--")

plt.xlabel("特征值")
plt.ylabel("目标值")
plt.title("不同深度回归决策树的拟合效果对比")
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

代码运行效果说明

1.会输出三个模型的 MSE（均方误差），深度为 5 的模型通常 MSE 最小；

2.可视化图中：深度 = 2 的曲线很 "平缓"，欠拟合；深度 = 5 的曲线贴合数据且不夸张，拟合效果最好；无深度限制的曲线 "锯齿状"，过拟合（把训练集的噪声也拟合了）。

---

9.3 剪枝

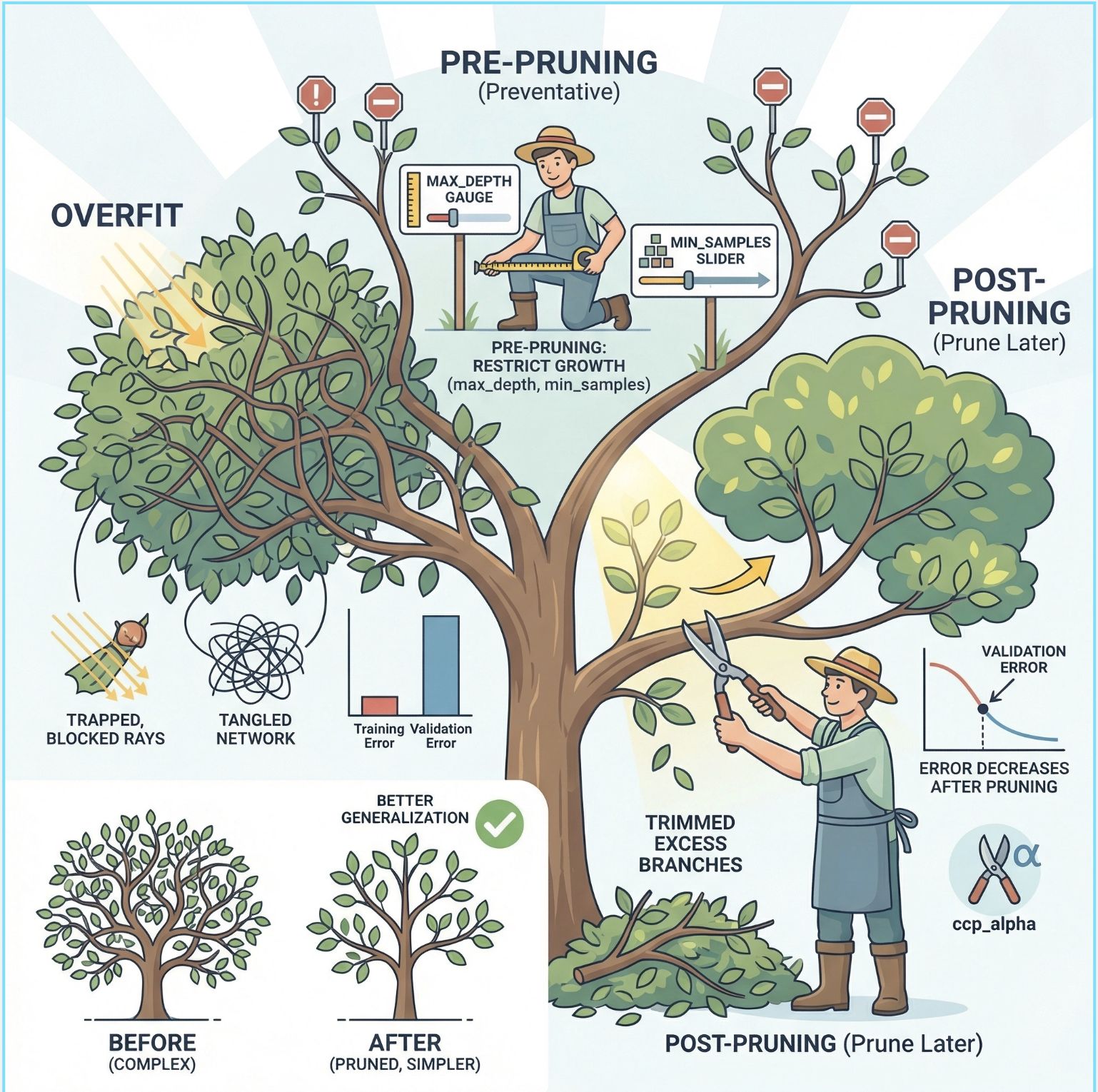
决策树天生容易 "长太满"（过拟合）------ 就像一棵树枝叶太茂盛，反而吸收不到阳光。剪枝就是 "剪掉多余的枝叶"，让树更简洁、泛化能力更强。

核心概念通俗解释

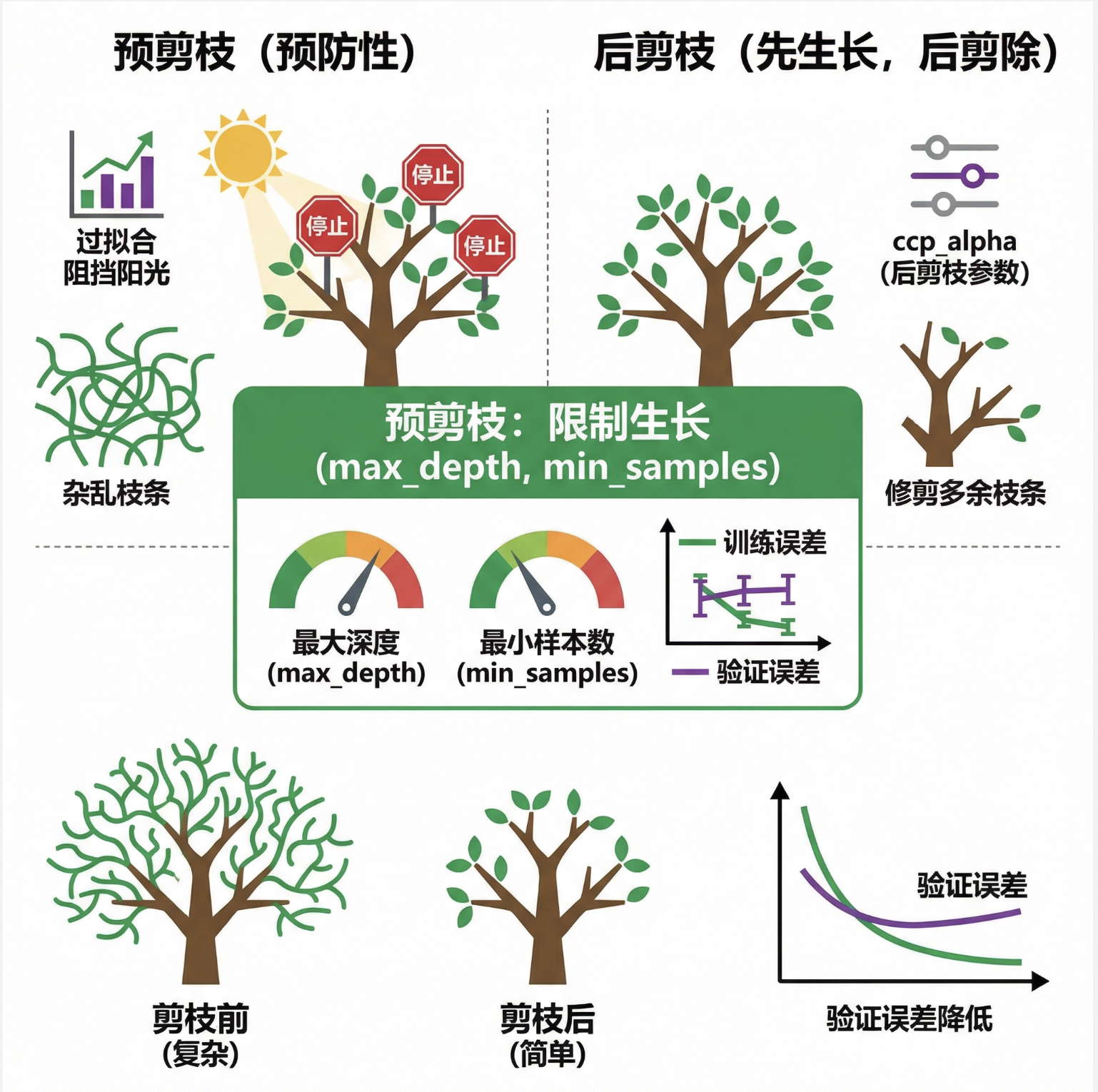
预剪枝 ："防患于未然"------ 在树生长过程中就限制它（比如设置max_depth、min_samples_split），前面代码中设置max_depth就是预剪枝；

后剪枝 ："先长后剪"------ 先让树长到最完整，再从叶子节点往上剪，去掉那些对模型性能提升很小的分支（sklearn 中ccp_alpha参数就是后剪枝的核心）。

完整可运行代码（剪枝效果对比）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# ====================== Mac系统Matplotlib中文显示配置 ======================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# ====================== 1. 加载数据 ======================
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ====================== 2. 后剪枝（ccp_alpha）效果对比 ======================
# 生成不同的ccp_alpha值（剪枝强度，值越大剪得越狠）
ccp_alphas = np.linspace(0, 0.1, 20)
train_accs = []
test_accs = []
trees = []

for ccp_alpha in ccp_alphas:
    tree = DecisionTreeClassifier(ccp_alpha=ccp_alpha, random_state=42)
    tree.fit(X_train, y_train)
    trees.append(tree)
    train_accs.append(accuracy_score(y_train, tree.predict(X_train)))
    test_accs.append(accuracy_score(y_test, tree.predict(X_test)))

# ====================== 3. 可视化剪枝效果 ======================
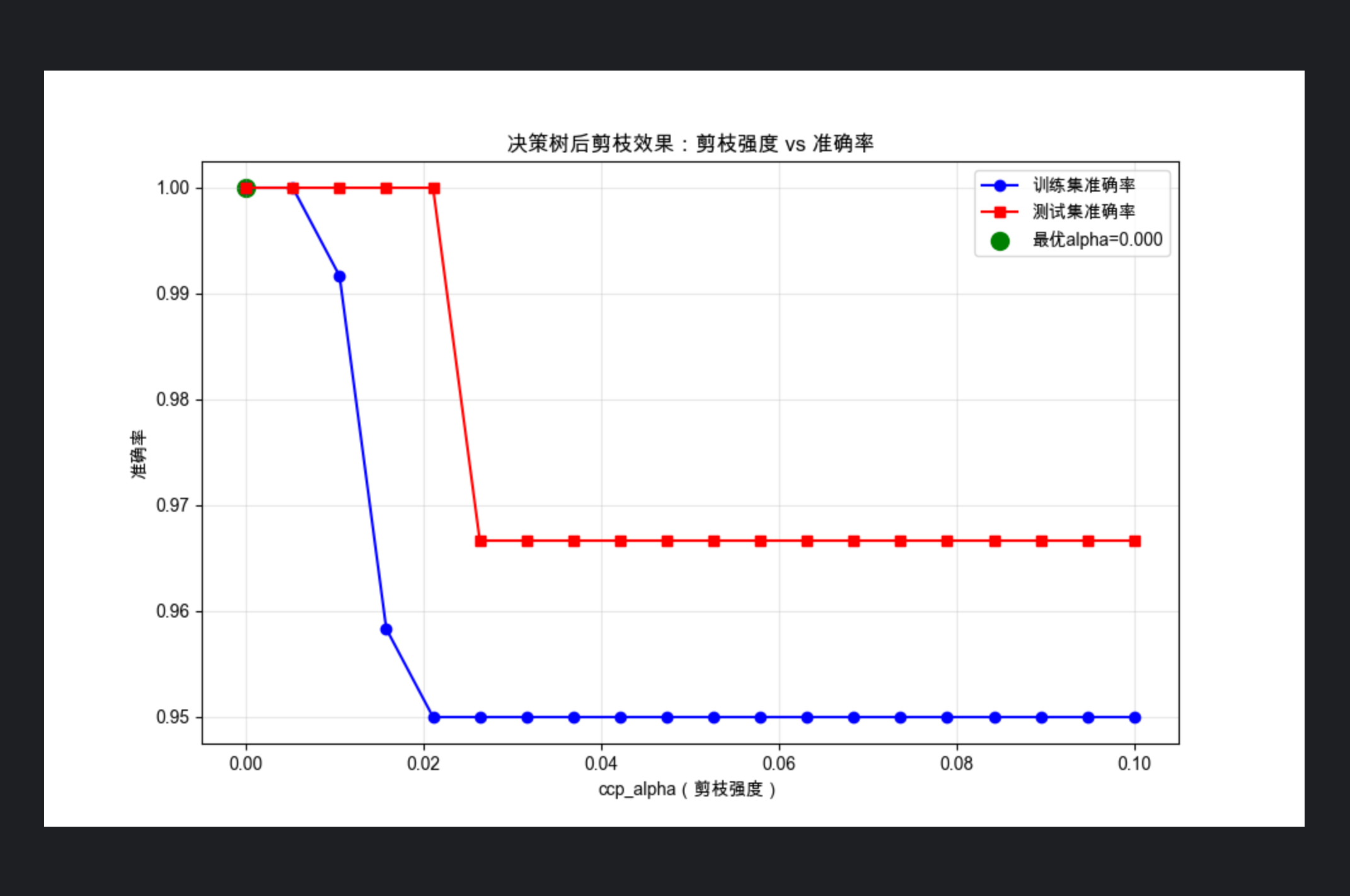
plt.figure(figsize=(10, 6))
plt.plot(ccp_alphas, train_accs, label="训练集准确率", marker="o", color="blue")
plt.plot(ccp_alphas, test_accs, label="测试集准确率", marker="s", color="red")
plt.xlabel("ccp_alpha（剪枝强度）")
plt.ylabel("准确率")
plt.title("决策树后剪枝效果：剪枝强度 vs 准确率")
plt.legend()
plt.grid(True, alpha=0.3)

# 找到测试集准确率最高的ccp_alpha
best_alpha_idx = np.argmax(test_accs)
best_alpha = ccp_alphas[best_alpha_idx]
plt.scatter(best_alpha, test_accs[best_alpha_idx], color="green", s=100, label=f"最优alpha={best_alpha:.3f}")
plt.legend()
plt.show()

# ====================== 4. 最优剪枝模型 vs 无剪枝模型 ======================
# 最优剪枝模型
best_tree = DecisionTreeClassifier(ccp_alpha=best_alpha, random_state=42)
best_tree.fit(X_train, y_train)

# 无剪枝模型
no_prune_tree = DecisionTreeClassifier(ccp_alpha=0, random_state=42)
no_prune_tree.fit(X_train, y_train)

print(f"无剪枝模型测试集准确率：{accuracy_score(y_test, no_prune_tree.predict(X_test)):.2f}")
print(f"最优剪枝模型测试集准确率：{accuracy_score(y_test, best_tree.predict(X_test)):.2f}")
print(f"无剪枝模型节点数：{no_prune_tree.get_n_leaves()}")
print(f"最优剪枝模型节点数：{best_tree.get_n_leaves()}")

代码运行效果说明

1.第一个图展示 "剪枝强度" 和 "准确率" 的关系：ccp_alpha 太小（剪得太少）测试集准确率低（过拟合），太大（剪得太狠）准确率也低（欠拟合）；

2.输出结果能看到：剪枝后模型节点数减少（更简洁），但测试集准确率反而更高（泛化能力提升）。

---

9.4 由决策树提取规则

决策树的一大优势是 "可解释性"------ 我们可以把训练好的决策树转换成 "if-else" 规则，比如：

if 花萼长度 <= 5.45 and 花萼宽度 > 2.85: 则为setosa品种
if 花萼长度 > 5.45 and 花瓣长度 <= 4.75: 则为versicolor品种

完整可运行代码（提取决策树规则）

from sklearn.tree import DecisionTreeClassifier, _tree
from sklearn.datasets import load_iris

# ====================== 1. 训练决策树 ======================
iris = load_iris()
X, y = iris.data, iris.target
feature_names = iris.feature_names
class_names = iris.target_names

tree = DecisionTreeClassifier(max_depth=2, random_state=42)
tree.fit(X, y)

# ====================== 2. 定义提取规则的函数 ======================
def tree_to_rules(tree, feature_names, class_names):
    tree_ = tree.tree_
    feature_name = [feature_names[i] if i != _tree.TREE_UNDEFINED else "undefined!" for i in tree_.feature]
    
    rules = []  # 存储最终规则
    
    def recurse(node, depth, rule):
        # 递归遍历树节点
        if tree_.feature[node] != _tree.TREE_UNDEFINED:
            # 内部节点：继续递归
            name = feature_name[node]
            threshold = tree_.threshold[node]
            
            # 左分支：<= threshold
            rule_left = rule + [f"{name} <= {threshold:.2f}"]
            recurse(tree_.children_left[node], depth + 1, rule_left)
            
            # 右分支：> threshold
            rule_right = rule + [f"{name} > {threshold:.2f}"]
            recurse(tree_.children_right[node], depth + 1, rule_right)
        else:
            # 叶子节点：生成规则
            class_idx = np.argmax(tree_.value[node][0])
            class_name = class_names[class_idx]
            rule_str = "if " + " and ".join(rule) + f" then 类别 = {class_name}"
            rules.append(rule_str)
    
    recurse(0, 1, [])
    return rules

# ====================== 3. 提取并打印规则 ======================
rules = tree_to_rules(tree, feature_names, class_names)
print("决策树提取的规则：")
for i, rule in enumerate(rules):
    print(f"规则{i+1}：{rule}")

代码运行效果说明

运行后会输出清晰的 "if-else" 规则，比如：

决策树提取的规则：
规则1：if petal length (cm) <= 2.45 then 类别 = setosa
规则2：if petal length (cm) > 2.45 and petal width (cm) <= 1.75 then 类别 = versicolor
规则3：if petal length (cm) > 2.45 and petal width (cm) > 1.75 then 类别 = virginica

---

9.5 由数据学习规则

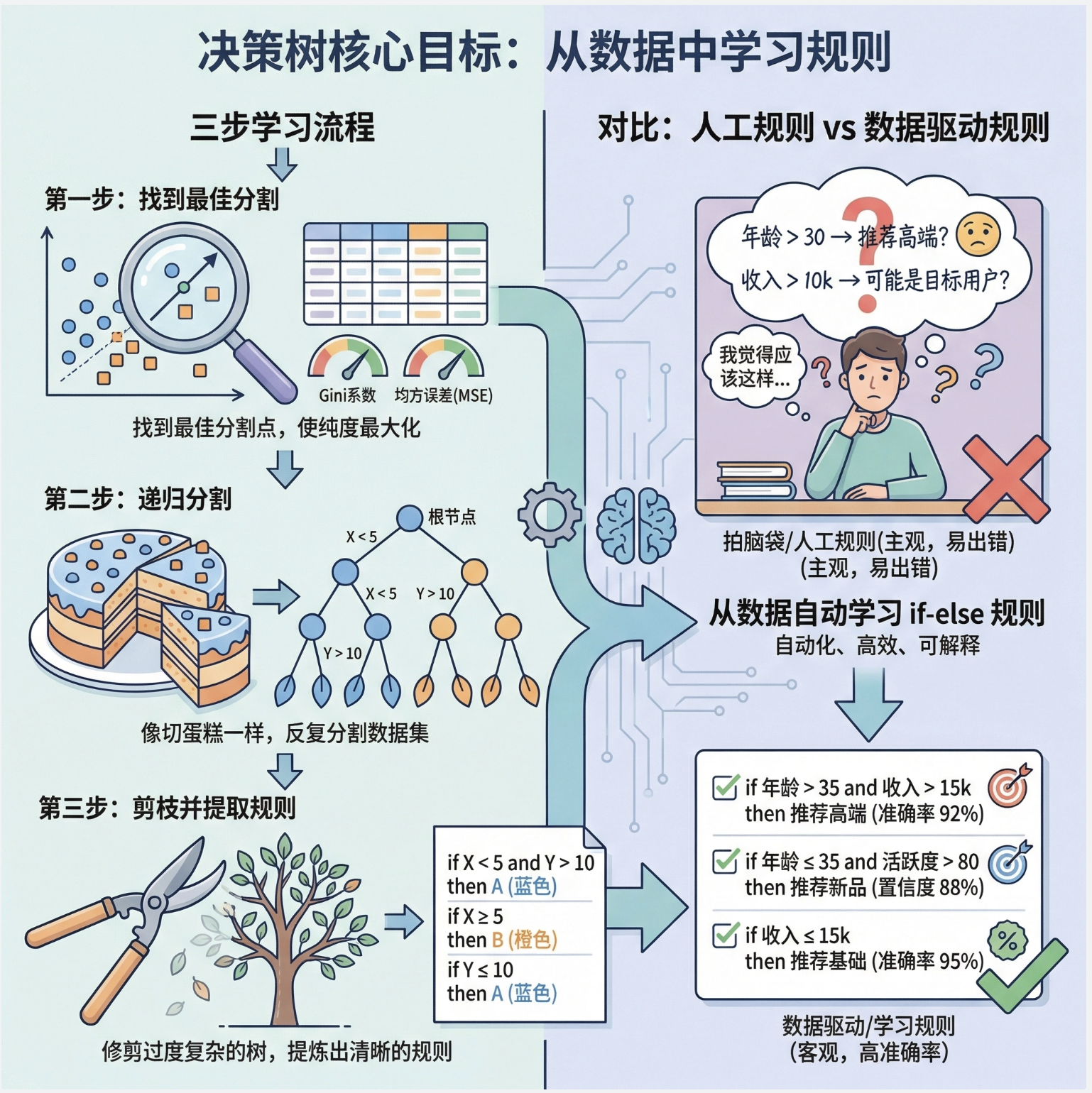
"由数据学习规则" 本质是决策树的核心目标 ------ 从原始数据中自动学习出 "if-else" 规则，而不是人工制定规则。

这个过程可以总结为 3 步：

1. 从数据中找 "最优切分特征"（比如用基尼系数 / MSE）；
2. 递归切分数据，生成决策树；
3. 剪枝优化，提取可解释的规则。

核心区别 ：人工规则是 "拍脑袋"（比如凭经验定 "年龄 > 30 则推荐高端产品"），而决策树学习的规则是 "数据驱动"（从数据中找最有效的切分点）。

这里复用 9.4 的代码即可 ------ 代码中训练决策树的过程，就是 "由数据学习规则" 的过程。

---

9.6 多变量树

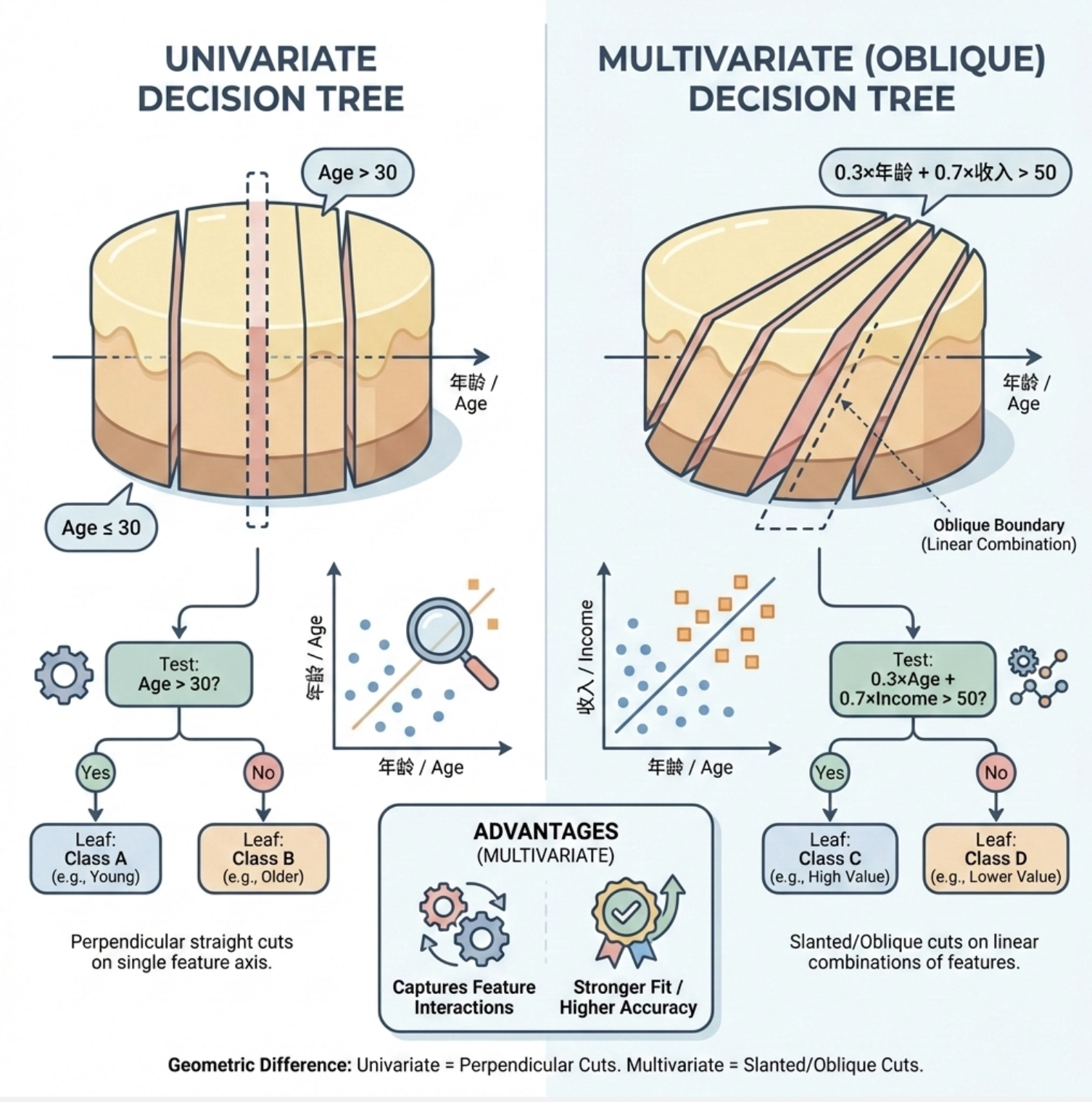
单变量树每次只看一个特征，而多变量树 每次切分基于多个特征的线性组合 （比如 "0.3× 年龄 + 0.7× 收入> 50"），可以理解为 "决策树 + 线性模型" 的结合体。

多变量树的优势：能捕捉特征之间的交互关系，拟合能力更强（比如 sklearn 中的DecisionTreeClassifier其实支持多变量，但默认是单变量切分；更典型的是 "斜决策树"）。

完整可运行代码（多变量树 vs 单变量树对比）

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import GradientBoostingClassifier  # 间接体现多变量效果
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# ====================== Mac系统Matplotlib中文显示配置 ======================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'

# ====================== 1. 生成非线性可分数据 ======================
# 生成2个特征的非线性可分数据（单变量树难拟合，多变量树更优）
X, y = make_classification(n_samples=500, n_features=2, n_informative=2,
                           n_redundant=0, n_clusters_per_class=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ====================== 2. 训练模型 ======================
# 单变量决策树（普通决策树）
single_var_tree = DecisionTreeClassifier(max_depth=3, random_state=42)
single_var_tree.fit(X_train, y_train)

# 多变量树（用梯度提升树模拟，其基学习器是多变量切分的树）
multi_var_tree = GradientBoostingClassifier(max_depth=3, n_estimators=10, random_state=42)
multi_var_tree.fit(X_train, y_train)

# ====================== 3. 模型评估 ======================
single_acc = accuracy_score(y_test, single_var_tree.predict(X_test))
multi_acc = accuracy_score(y_test, multi_var_tree.predict(X_test))

print(f"单变量树测试集准确率：{single_acc:.2f}")
print(f"多变量树测试集准确率：{multi_acc:.2f}")

# ====================== 4. 可视化决策边界对比 ======================
def plot_boundary(clf, X, y, title, ax):
    h = 0.02
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    ax.contourf(xx, yy, Z, alpha=0.75, cmap=plt.cm.RdBu)
    ax.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap=plt.cm.RdBu)
    ax.set_title(title)
    ax.set_xlabel("特征1")
    ax.set_ylabel("特征2")

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
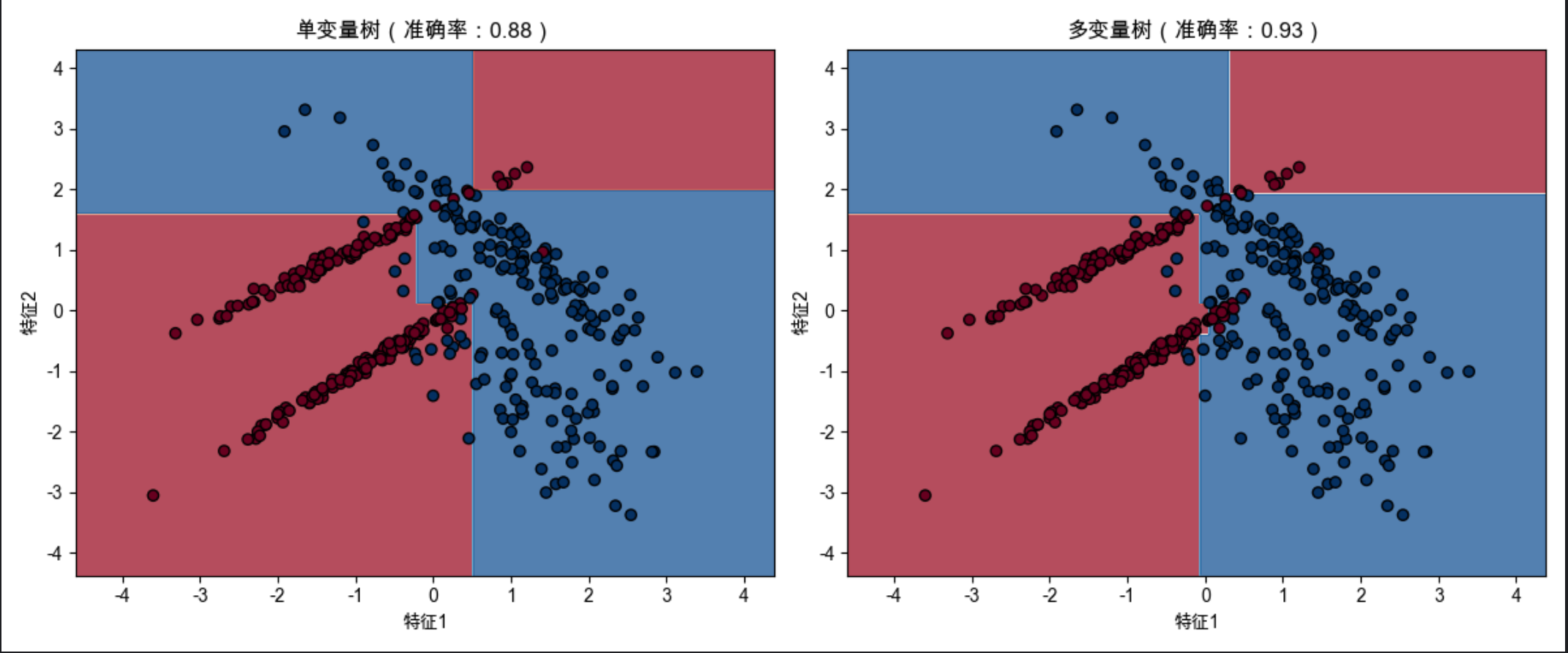
plot_boundary(single_var_tree, X_train, y_train, 
              f"单变量树（准确率：{single_acc:.2f}）", ax1)
plot_boundary(multi_var_tree, X_train, y_train, 
              f"多变量树（准确率：{multi_acc:.2f}）", ax2)
plt.tight_layout()
plt.show()

代码运行效果说明

1.多变量树的准确率通常高于单变量树；

2.可视化图中：单变量树的决策边界是 "轴平行" 的（只沿 x 或 y 轴切分），多变量树的边界是 "斜的"（基于多个特征的组合切分），更贴合非线性数据的分布。

---

9.7 注释

1.决策树的 "贪心"：每次切分只选当前最优的特征，不考虑全局最优，可能导致局部最优但全局次优；

2.特征重要性：决策树可以输出feature_importances_属性，衡量每个特征对决策的贡献度；

3.缺失值处理：sklearn 的决策树会自动处理缺失值（用其他样本的特征值分布来替代）；

4.类别特征处理：需要先将类别特征编码（比如 One-Hot 编码），决策树不直接支持字符串类型的特征。

---

9.8 习题

1.基于本文的分类树代码，尝试修改criterion参数（从gini改为entropy），对比两种纯度指标的效果；

2.基于回归树代码，调整min_samples_leaf参数（比如设置为 5、10），观察 MSE 的变化；

3.用自己的数据集（比如房价数据集、客户流失数据集），训练决策树并提取规则；

4.尝试用Graphviz可视化决策树（需要安装graphviz库和软件），对比本文的plot_tree效果。

---

9.9 参考文献

1. 《机器学习导论》（原书第 4 版），Ethem Alpaydin 著；
2. 《机器学习》（周志华 著），第 4 章 决策树；
3. Scikit-learn 官方文档：https://scikit-learn.org/stable/modules/tree.html；
4. 《统计学习方法》（李航 著），第 5 章 决策树。

---

总结

1.决策树核心是 "分而治之"：分类树用基尼 / 信息熵选特征，回归树用 MSE 选特征，单变量树轴平行切分，多变量树支持特征组合切分；

2.剪枝是解决决策树过拟合的关键：预剪枝（限制深度）简单高效，后剪枝（ccp_alpha）更精准；

3.决策树的最大优势是可解释性：能提取 "if-else" 规则，这是深度学习等黑箱模型不具备的核心特点。