1 今日打卡
2 N皇后
2.1 思路
将 N 皇后的摆放问题转化为 "逐行放置皇后,且每放置一个皇后都检查是否与已放置的皇后冲突"。
回溯核心:
选择:在当前行的某一列放置皇后;
约束:皇后不能同行、同列、同斜线;
终止:当行数等于 N 时,说明所有皇后都合法放置,记录结果;
回溯:如果当前列放置后后续无法完成,撤销当前列的皇后,尝试下一列。
结果转换:将字符数组形式的棋盘转换为字符串列表,方便返回结果。
难点:这些函数要传入什么参数、以及回溯的思想,每一层递归选一行,有一个参数row来控制。每一行里回溯遍历row的每一个格子。因此判断合法性的时候,不需要判断row这个维度。
2.2 实现代码
java
class Solution {
// 最终结果:存储所有合法的N皇后摆放方案
List<List<String>> res = new ArrayList<>();
/**
* 主方法:解决N皇后问题的入口
* @param n 皇后的数量(也是棋盘的大小 n*n)
* @return 所有合法的摆放方案,每个方案是一个字符串列表,代表棋盘的每一行
*/
public List<List<String>> solveNQueens(int n) {
// 初始化棋盘:n行n列,所有位置初始化为 '.'(表示空)
char[][] chessboard = new char[n][n];
for (int i = 0; i < n; i++) {
Arrays.fill(chessboard[i], '.');
}
// 从第0行开始回溯,尝试放置皇后
backtracking(0, n, chessboard);
// 返回所有合法方案
return res;
}
/**
* 回溯方法:逐行放置皇后,递归+回溯尝试所有可能
* @param row 当前处理的行(从0开始)
* @param n 棋盘大小/皇后数量
* @param chessboard 当前的棋盘状态
*/
public void backtracking(int row, int n, char[][] chessboard) {
// 终止条件:当处理的行数等于n时,说明所有皇后已合法放置
if (row == n) {
// 将当前棋盘(字符数组)转换为字符串列表,加入结果集
res.add(Array2List(chessboard));
return;
}
// 遍历当前行的每一列,尝试放置皇后
for (int col = 0; col < n; col++) {
// 检查当前位置 (row, col) 是否可以放置皇后(无冲突)
if (isValid(row, col, n, chessboard)) {
// 选择:在当前位置放置皇后 'Q'
chessboard[row][col] = 'Q';
// 递归:处理下一行
backtracking(row + 1, n, chessboard);
// 回溯:撤销选择,将皇后移除(恢复为 '.'),尝试下一列
chessboard[row][col] = '.';
}
}
}
/**
* 合法性检查:判断 (row, col) 位置是否可以放置皇后
* 只需检查「上方」的冲突(因为是逐行放置,当前行及下方无皇后):
* 1. 同列是否有皇后
* 2. 左上到右下的斜线(↖️)是否有皇后
* 3. 右上到左下的斜线(↗️)是否有皇后
* @param row 当前行
* @param col 当前列
* @param n 棋盘大小
* @param chessboard 棋盘状态
* @return true=可以放置,false=不可放置
*/
public boolean isValid(int row, int col, int n, char[][] chessboard) {
// 1. 检查同列:遍历当前行上方的所有行,看同一列是否有皇后
for (int i = 0; i < row; i++) {
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 2. 检查左上斜线(row-1, col-1)方向:往左上角遍历
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 3. 检查右上斜线(row-1, col+1)方向:往右上角遍历
for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 无冲突,可放置
return true;
}
/**
* 辅助方法:将字符数组形式的棋盘转换为字符串列表
* @param chessboard 字符数组棋盘
* @return 每行对应一个字符串的列表
*/
public List<String> Array2List(char[][] chessboard) {
List<String> list = new ArrayList<>();
for (char[] row : chessboard) {
// 将每行的字符数组转换为字符串,加入列表
list.add(new String(row));
}
return list;
}
}3 解数独
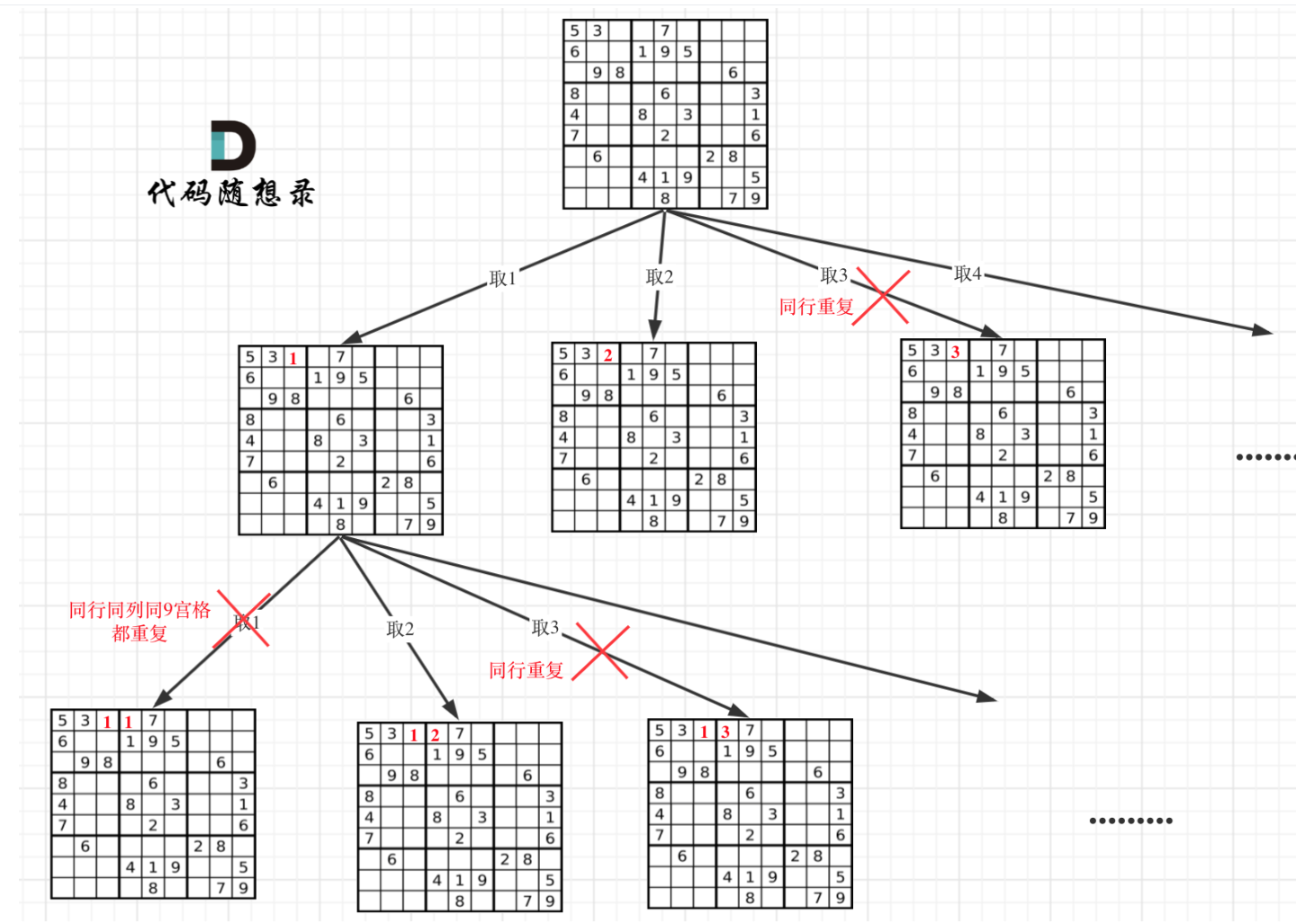
3.1 思路
想象你手里有一张空白数独(只有部分数字),你要填完它,规则是每行 / 每列 / 每个 3×3 九宫格数字不重复。你的操作步骤会是这样:
找空白格:从第一行第一列开始,逐个找空位置(.);
试填数字:对这个空白格,先试填 1,检查是否符合规则;
验证后续:如果 1 合法,就继续填下一个空白格;如果下一个空白格能填完所有数(找到解),游戏结束;
试错回溯:如果填 1 后,后面的空白格怎么填都不合法,说明 1 填错了,把 1 擦掉(恢复.),再试填 2;
彻底失败:如果 1-9 都试了,这个空白格都填不了,说明上一个空白格填的数错了,回到上一个格换数;
成功终止:一旦所有空白格都填完且合法,立刻停止所有操作,不用再试其他数字。
代码里的回溯逻辑,就是把上面的 "人工操作" 翻译成代码,核心是递归代替 "填下一个格",boolean 返回值代替 "是否找到解"。
回溯函数要设计成boolean返回值,有点绕。因为解数独找到一个符合的条件(就在树的叶子节点上)立刻就返回,相当于找从根节点到叶子节点一条唯一路径,所以需要使用bool返回值。
3.2 实现代码
java
class Solution {
// 主方法:解数独的入口,外部调用这个方法即可
// 作用:直接启动回溯过程,修改传入的board数组(数独解会直接填充在原数组中)
public void solveSudoku(char[][] board) {
backtracking(board);
}
/**
* 回溯核心函数:尝试填充数独,返回是否找到合法解
* 核心逻辑:逐格试填,递归验证,失败回溯,成功终止
* @param board 数独棋盘(会被直接修改)
* @return true = 找到合法解(终止所有递归);false = 当前格试完1-9都不行,需要回溯
*/
public boolean backtracking(char[][] board) {
// 第一步:遍历整个棋盘,找空白格(逐行逐列)
// i代表行,从0到8(数独共9行)
for(int i = 0; i < 9; i++) {
// j代表列,从0到8(数独共9列)
for(int j = 0; j < 9; j++) {
// 如果当前格不是空白(有原始数字),直接跳过,不处理
if(board[i][j] != '.') continue;
// 第二步:对空白格,尝试填1-9(字符型'1'到'9')
for(char k = '1'; k <= '9'; k++) {
// 检查:当前格填k是否符合数独规则(同行/同列/同九宫格无重复)
if(isValid(board, i ,j , k)) {
// 选择:如果合法,就把k填进当前格
board[i][j] = k;
// 第三步:递归处理下一个空白格(核心!)
// 调用backtracking后,如果返回true,说明"后续所有格都填对了,找到解了"
if(backtracking(board)) {
// 立刻返回true,终止所有递归(不用再试其他数字)
return true;
}
// 第四步:回溯(关键!)
// 如果递归返回false,说明"填k后,后续格无法填完",k是错的
// 把当前格恢复为空白,继续试下一个数字
board[i][j] = '.';
}
}
// 第五步:当前格试完1-9都不行,返回false
// 告诉上一层递归:"我这格填不了,你上一格填的数错了,赶紧换一个"
return false;
}
}
// 第六步:遍历完所有格(没有空白格了),说明所有数都填对了
// 返回true,告诉上一层"找到解了"
return true;
}
/**
* 合法性检查函数:判断(row, col)位置填val是否符合数独规则
* 检查维度:1.同列 2.同行 3.同九宫格
* @param board 数独棋盘
* @param row 要填数的行号
* @param col 要填数的列号
* @param val 要填的数字(字符型,如'1')
* @return true=合法,false=不合法
*/
public boolean isValid(char[][] board, int row, int col, char val) {
// 1. 检查同列:遍历当前列的所有行,看是否有和val重复的数字
for(int i = 0; i < 9; i++) {
if(board[i][col] == val) {
return false; // 同列有重复,不合法
}
}
// 2. 检查同行:遍历当前行的所有列,看是否有和val重复的数字
for(int j = 0; j < 9; j++) {
if(board[row][j] == val) {
return false; // 同行有重复,不合法
}
}
// 3. 检查同九宫格:找到当前格所在九宫格的起始位置,遍历九宫格内所有格
int startRow = (row / 3) * 3; // 九宫格起始行(0/3/6)
int startCol = (col / 3) * 3; // 九宫格起始列(0/3/6)
// 遍历九宫格的3行
for(int i = startRow; i < startRow + 3; i++) {
// 遍历九宫格的3列
for(int j = startCol; j < startCol + 3; j++) {
if(board[i][j] == val) {
return false; // 九宫格内有重复,不合法
}
}
}
// 所有检查通过,合法
return true;
}
}