本文因有人考公而记录,我觉得不记录估计过几天大家就不记得怎么回事了。
作为一个学计算机的,早期学过一点算法,也学过一点微积分,看到错位排列的推导式的时候感觉死去的记忆在疯狂攻击我。这里从小白的角度来一点一点解释错位排列的推导式到底是怎么推导出来的。
因为我知道AI说话比较晦涩,比较高级,它的解释虽然能让人听懂,但是对我来说是有理解门槛的。所以我这篇文章也就不让AI横插一笔来润色了。
文章目录
何为递推?
没错,第一步应该是解释什么叫做递推!因为如果不是学计算机的,甚至也没学过高数的话,可能大家完全不知道递推是什么意思!
递推其实就是高中数学的数学归纳法,但是我知道很多人的高中数学也还给了老师,所以这里抛开所有乱七八糟的概念,也不使用任何的Markdown公式以防有人用的是手机渲染不出来。
递推的意思就是可以逐步推导出最后的结果,记住"从小问题推导出大问题的结果"就好了。
比如我今天吃一个苹果,明天吃两个苹果,每天多吃一个苹果,那第n天我肯定是吃n个苹果。
把"我每天吃多少个苹果"作为一个问题,那么,把我第n天吃多少个苹果记作问题n,把我第(n-1)天吃多少个苹果记作问题(n-1),那么很显然,问题n的答案 = 问题(n-1)的答案 + 1。这其实就是递推。

此时就有人要问了:那你直接记作n不就得了,为什么要说这是什么递推递推的,不是很懂。
------这是因为问题太过复杂的时候,记递推式会比记最终的算式简单得多呀!
比如再举一个例子:
我今天吃一个苹果,明天吃两个苹果,每天吃的苹果是前两天吃的苹果数量之和。
此时递推式是 问题n的答案 = 问题(n-1)的答案 + 问题(n-2)的答案。

这个时候问题n的答案并不是能够那么简单推出来的!但是也是可以推出来的,如果你想推出来这个通项公式,可以用设设特征方程 (线性代数教的)的方式或者设母函数(高中数学教的),也可以用其他的更高级的方式,这里就不多说了。这里的答案,实际答案是斐波那契数列的答案,也就是如图所示:
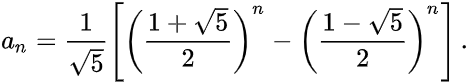
是吧,很复杂。
所以如果能搞到递推式,很多问题真的很简单就能算出来了。
所以,我们应首先具备判断问题的性质的能力,并具备将问题定性为一个完整的问题和问题的答案的意识;而不是在看到一个问题的时候,直接把它看成所谓的n,或者直接求出问题的结果。
请,允许中间问题存在,允许问题暂时得不到结果。
何为错位排列?
错位排列其实就是求位置错了的排列方案的种类数量的问题的合集。
比如周深开一场演唱会,有6万人,因为大家陷入了规则怪谈,所有人都不准坐自己的座位上,必须坐别人的座位上,那么求大家的坐法共有多少种。

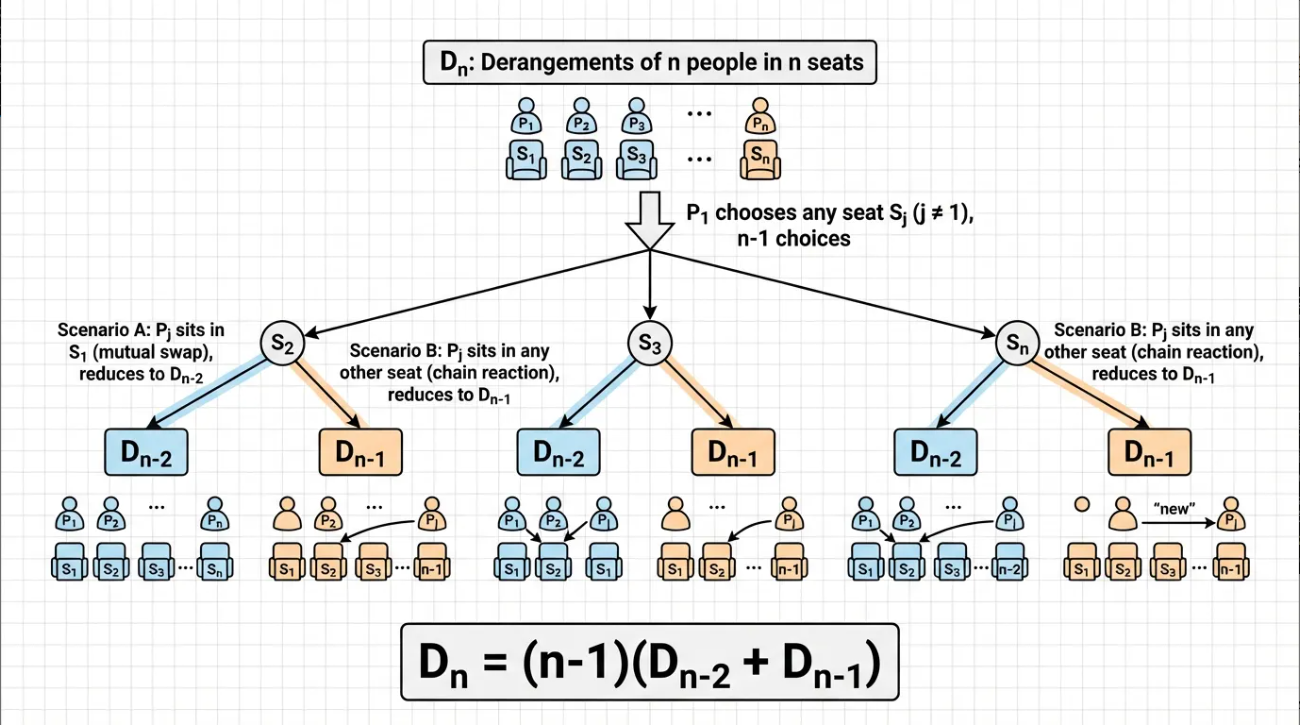
这种问题可以记作Dn,它有一个非常非常简明扼要的递推式:Dn=(n-1)(Dn-2 + Dn-1)。这个题里n=6万。
这种问题可以定性成:总共n个空位,每个人都有一个禁止去的座位,且每个人的禁位不同。【注意这里最好忽略这个禁位和本人的对应关系,不然思考问题的时候容易陷入"禁止坐的是本人的座位呀,不是abc的座位,为啥禁止坐abc的作为也可以归类为这个问题"的怪圈中】
错位排列的递推式如何求?
我会给一个省流版和详细叙述版------因为我自己是那种只能接受省流版解释的人,但是并不是所有人都能看懂我省流完了在说什么,所以这里大家按需阅读。
省流版:第一个人坐其他位置有(n-1)种可能,而被它占位的人可以坐第一个人的位置(对应Dn-2的情况,因为它俩互占了导致其他人独立于它俩了),也可以不坐第一个人的位置(对应的是被它占位的人不能坐第一个位置、其他的位置都能坐+其他人不能坐自己的位置、其他的位置都能坐,即Dn-1这个子问题)。
所以合起来就是递推式 Dn = (n-1)(Dn-2 + Dn-1)。
如下图所示,展示第一个人选择座位的两种情况,以及对应的递推关系 Dn = (n-1)(Dn-2 + Dn-1)。
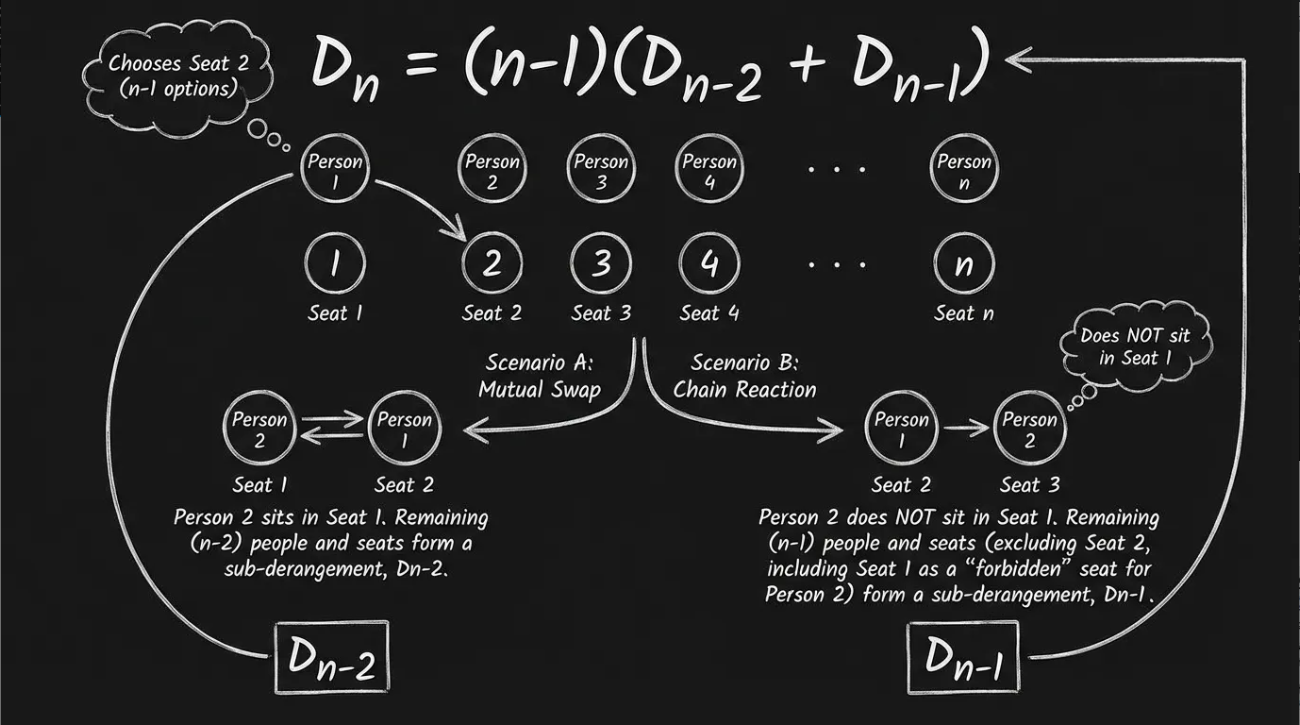
详细版:
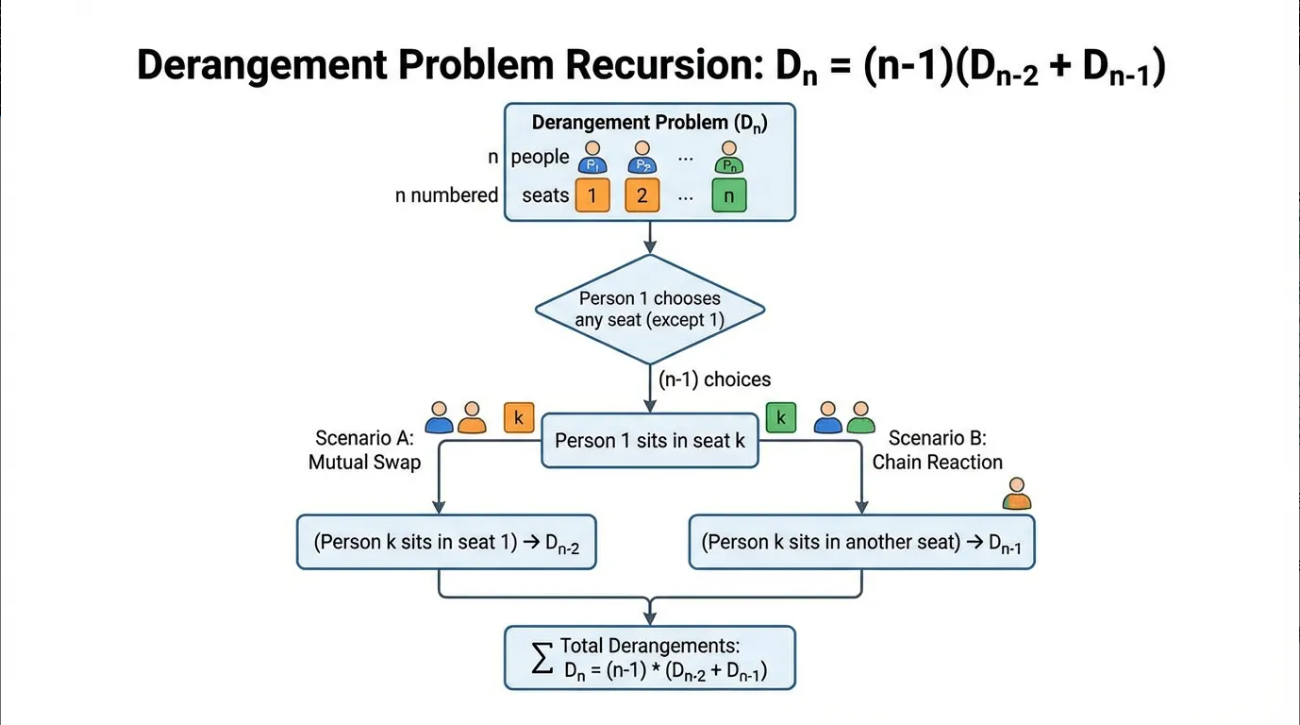
首先,以流程图的形式,展示递推关系的完整结构,这是整个推导过程的思维导图:
要推导 Dn,咱们先看第1个人。比如假设是我,买到了周深的第一排的第一号座位,我被要求不能坐自己的位子,那我就有 n-1 种选位子的可能。
假设我坐了第2个人的位子,这时候压力给到了第2个人,会出现两种纯粹的局面:
-
局面 A(互换成功): 第2个人心想"你不仁我不义",反手坐了第1个人的位子。好,我俩直接相互抵消离场,剩下 n-2 个人继续玩错位。这部分的方案数就是 Dn-2。
-
局面 B(接力甩锅): 第2个人偏不坐第1个人的位子,他要去占别人的。此时对于第2个人来说,第1个人的位子就成了他的"新禁区"。这局面就变成了:包括第2个人在内的 n-1 个人,每个人都有一个专属禁区。这本质上就是缩小了一号的错位问题,方案数就是 Dn-1。
把这两种独立的情况加起来,再乘上第1个人最初的那 n-1 种选择,递推式 Dn = (n-1)(Dn-2 + Dn-1) 就成了。
如果你无法理解为什么我有(n-1)种选位置的可能性,或者无法理解为什么要乘以(n-1)而不是加上(n-1),可以看这张图片,递归结构的树状图,清晰展示两种情况的分支:
简单来说:错位排列要么是两人互换(规模缩减2),要么是多人乱传(规模缩减1),全看被占位的那人选不选第一个人的位子。这样分类讨论能够覆盖所有的情况,所以能够用这种分类讨论去解决这个问题。
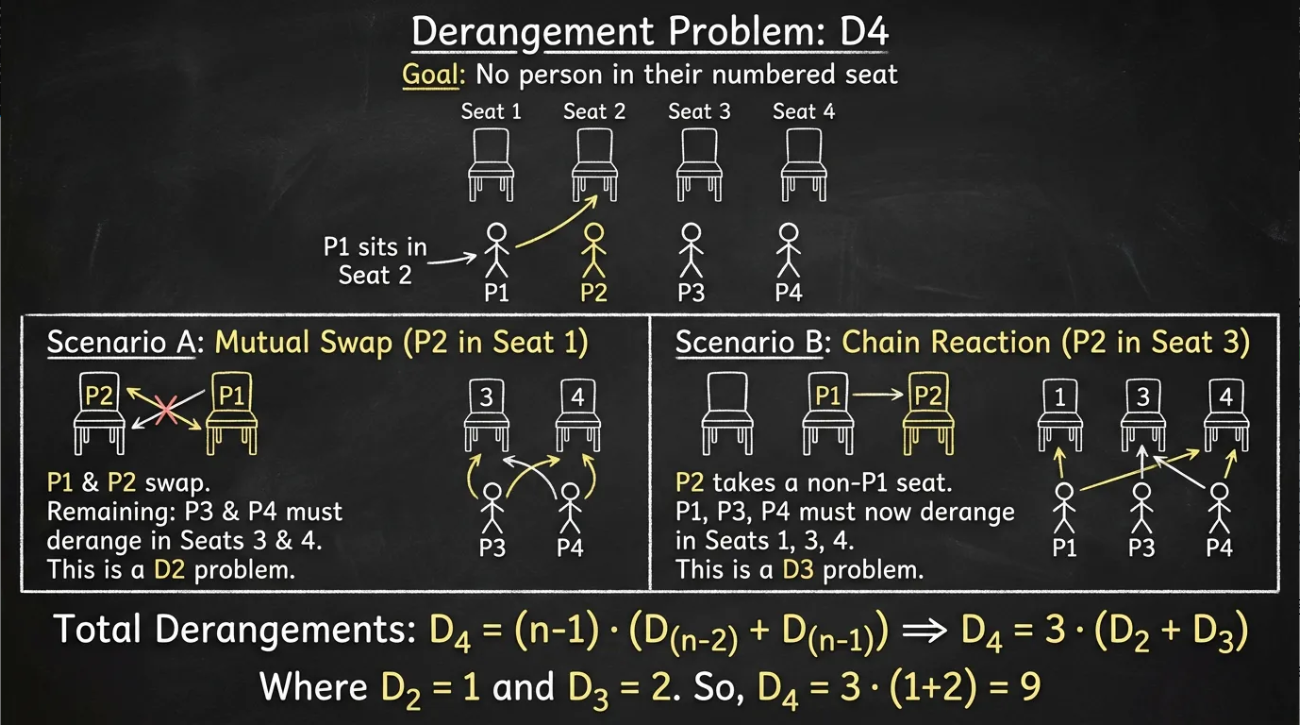
例如,当n等于4的时候,完整的推导过程如下图所示:
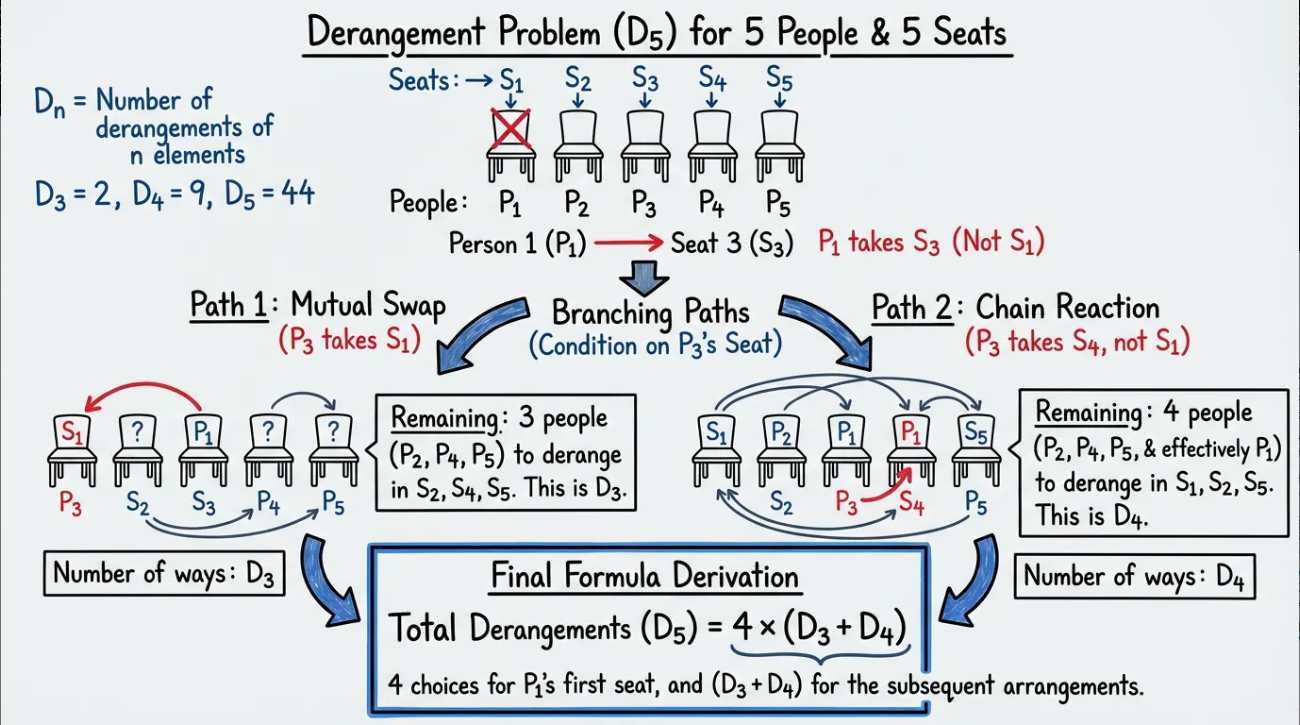
例如,当 n=5 的具体例子展示递推过程,假设第一个人坐第 3 个座位,分支为 D3 和 D4:
公考小tips
如果你连递推式也背不下,也没办法理解推导过程,那么你可以只记问题的性质,和前面几位的结果:
D2=1
D3=2
D4=9
D5=44
如果你连结果都记不住!那你可以记住,这种问题,每个参与者都是平等的,所以你会发现只要考虑某个参与者在某位的所有的排列方式(通过枚举),就可以算出其他的参与者。所以!它一定是(n-1)倍!这样往往就已经可以排除选择题的其他选项了。
本账号所有文章均为原创,欢迎转载,请注明文章出处:https://shandianchengzi.blog.csdn.net/article/details/157874394。百度和各类采集站皆不可信,搜索请谨慎鉴别。技术类文章一般都有时效性,本人习惯不定期对自己的博文进行修正和更新,因此请访问出处以查看本文的最新版本。