决策树之回归树：核心知识点与实操指南

一、回归树的基础认知：从决策树到回归树

1. 决策树的通用核心逻辑

回归树是决策树的子类，先明确决策树的通用概念：决策树通过对训练样本的学习建立层级化分类/回归规则，所有数据从根节点出发，经非叶子节点的特征判断逐步分枝，最终落到叶子节点得到预测结果，属于典型的有监督学习。

决策树的结构包含三类核心节点：

根节点：整个树的第一个判断节点，是所有数据的入口；
非叶子节点：中间的特征判断节点，负责数据的分枝；
叶子节点：最终的结果节点，回归树的叶子节点为连续型数值 ，分类树的叶子节点为离散的类别标签。

2. 回归树与分类树的核心区别

决策树分为分类树（DecisionTreeClassifier）和回归树（DecisionTreeRegressor），二者核心差异体现在任务目标 和节点分裂/评判依据上：

任务目标：分类树处理离散分类任务 ；回归树处理连续数值预测任务。
评判/分裂依据：分类树用基尼系数（gini）、熵值（entropy） 衡量节点纯度，用信息增益/信息增益率做分裂依据；回归树用均方误差（mse）、平均绝对误差（mae） 衡量预测误差，以此作为节点分裂的核心标准。
结果输出：分类树叶子节点为类别标签，回归树叶子节点为连续数值。

3. 回归树的核心基础：CART树

回归树的实现基于CART树（分类与回归树），CART树是一种二叉树结构，可同时支持分类和回归任务：针对分类任务用基尼系数，针对回归任务用均方误差。

二、Sklearn中回归树的核心API：DecisionTreeRegressor

在Python的Sklearn库中，回归树的官方API为sklearn.tree.DecisionTreeRegressor，是实操回归树的核心工具，其完整定义如下：

复制代码

class sklearn.tree.DecisionTreeRegressor(criterion='mse', splitter='best', max_depth=None,
 min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None,
 random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0,min_impurity_split=None, 
presort=False)

该API的参数与分类树高度重合，仅部分核心参数的默认值/适配性不同，下面对回归树的核心必调参数做详细解读，标注了参数的含义、默认值和实操建议：

1. 节点分裂/评判相关参数

criterion ：节点分裂的判断依据，默认mse（均方误差），可选mae（平均绝对误差）。

均方误差是回归任务的经典评判指标，平均绝对误差对异常值的鲁棒性更强；实操建议按默认选择mse即可，特殊异常值场景可切换为mae。

splitter ：节点的分裂策略，默认best（在所有特征中找最优切分点），可选random（在部分特征中随机找切分点）。

回归树的分裂策略与分类树一致，默认选择best即可，仅数据量极大、特征极多的场景可尝试random提升效率。

2. 树结构限制（防过拟合核心，预剪枝关键）

这类参数是回归树调优的核心，通过限制树的生长来防止过拟合，也是预剪枝的核心实现手段，所有参数均与分类树完全一致：

max_depth ：树的最大深度，默认None（不限制深度，树会完全展开，直到叶子节点满足最小样本数）。

过深的树会学习到训练集的噪声，是过拟合的主要原因；实操建议通过交叉验证选择合适值，样本/特征多的场景需主动限制。

min_samples_split ：分裂一个内部节点需要的最小样本数，默认2。

若某节点的样本数小于该值，则不再继续分裂；样本量极大时建议增大该值，避免无意义的细枝分裂。

min_samples_leaf ：叶子节点的最少样本数，默认1。

若某叶子节点的样本数小于该值，会与兄弟节点一起被剪枝；该参数从叶子节点层面限制树的生长，有效防止过拟合。

max_leaf_nodes ：树的最大叶子节点数，默认None（不限制），重要特性 ：设置该参数后，max_depth会失效。

通过限制叶子节点的总数来控制树的复杂度，特征多的场景可主动设置，具体值通过交叉验证得到。

max_features ：寻找最优分裂时需要考虑的特征数量，默认None（考虑所有特征），可选log2/sqrt/具体数值。

3. 其他辅助参数

random_state ：设置树分枝的随机种子，默认None。

特征数较多时，决策树的分枝会存在随机性，设置固定的random_state可确保每次运行代码得到相同的结果，保证实验的可复现性。

min_impurity_decrease/min_impurity_split：限制树的生长，若节点的不纯度（回归树为预测误差）小于阈值，则不再分裂，成为叶子节点；一般保持默认即可。
min_weight_fraction_leaf ：叶子节点的最小样本权重和，默认0（不考虑权重）。

仅在样本存在缺失值、或样本分布偏差极大时需要调整，常规回归任务无需关注。

presort ：是否对数据预排序，默认False，预排序可提升分裂效率，但会增加计算成本，大数据集不建议开启。

三、回归树的常用实操方法

Sklearn的DecisionTreeRegressor提供了一系列实用方法，用于获取树的信息、执行预测/分析，是回归树实操的重要工具，核心方法如下：

apply(X) ：返回数据集X中每个样本被预测后落到的叶子节点的索引，可用于分析样本的树路径分布；
decision_path(X) ：返回数据集X在树中的决策路径，可用于分析样本从根节点到叶子节点的特征判断过程；
get_depth() ：获取训练完成后回归树的实际深度，用于验证max_depth的设置效果；
get_n_leaves() ：获取训练完成后回归树的实际叶子节点数，用于验证max_leaf_nodes的设置效果；
get_params() ：获取回归树模型的所有参数配置信息，方便查看/调参验证；
score(X, y) ：计算模型在数据集(X,y)上的评判指标R²（决定系数），R²越接近1，模型的回归预测效果越好；
predict(X)：回归树的核心预测方法，输入特征集X，返回连续型的预测数值。

四、回归树的核心问题：过拟合与优化策略

回归树和所有决策树一样，若不做任何限制，会将训练集的所有细节（包括噪声）都学习到，导致模型在训练集上效果极好，在测试集上效果大幅下降的过拟合问题，这是回归树实操中需要解决的核心问题。

1. 过拟合的解决思路：剪枝

决策树的防过拟合核心手段是剪枝，剪枝分为预剪枝 和后剪枝。

2. 回归树的核心优化：预剪枝策略

预剪枝的核心思路是在树的生长过程中提前限制，阻止树过度展开 ，无需在树生成后再做裁剪，所有策略均通过调整上述树结构限制参数实现，核心预剪枝策略如下：

限制树的最大深度（max_depth）：最常用的核心参数，通过控制树的层级，避免树过度生长；
限制最大叶子节点数（max_leaf_nodes）：从结果节点层面限制树的复杂度，设置后会覆盖max_depth；
提高内部节点分裂的最小样本数（min_samples_split）：让少量样本的节点不再分裂，避免学习到噪声；
提高叶子节点的最小样本数（min_samples_leaf）：让少量样本的叶子节点被剪枝，减少无意义的细枝；
限制分裂时考虑的特征数（max_features）：减少特征维度，避免模型过度依赖个别特征的噪声。

五、回归树的适用场景与优缺点

1. 适用场景

回归树适合处理中低维度、非线性的连续数值预测任务 ，如房价预测、商品销量预估、气温预测、用户消费金额预测等，尤其适合需要模型可解释性的场景。

2. 优点

可解释性极强：树状结构的决策规则清晰，可直观看到特征对预测结果的影响；
无需特征预处理：无需对特征做标准化/归一化，对缺失值、异常值有一定的鲁棒性；
训练/预测速度较快：基于树的分枝逻辑，计算复杂度较低；
可处理非线性关系：无需手动构造特征，能自动学习特征与目标值的非线性关联。

3. 缺点

易过拟合：需通过大量调参实现模型泛化；
对训练集的微小变化敏感：训练集的少量数据变化可能导致树结构大幅改变；
预测精度有限：单一回归树的预测精度通常低于集成模型（如随机森林、XGBoost）。

六、示例

以电信客户流失数据为例，训练回归树，判断客户类型是否流失。

复制代码

import pandas as pd
from sklearn import metrics

#定义绘制混淆矩阵函数
def cm_plot(y,yp):
    from sklearn.metrics import confusion_matrix
    import matplotlib.pyplot as plt

    cm=confusion_matrix(y,yp)
    plt.matshow(cm,cmap=plt.cm.Blues)
    plt.colorbar()
    for x in range(len(cm)):
        for y in range (len(cm)):
            plt.annotate(cm[x,y],xy=(y,x),horizontalalignment='center',verticalalignment='center')
            plt.ylabel('True label')
            plt.xlabel('Predicted label')
    return plt

#导入数据
datas=pd.read_excel("电信客户流失数据.xlsx")
data=datas.iloc[:,:-1]
target=datas.iloc[:,-1]

#切分数据
from sklearn.model_selection import train_test_split
data_train,data_test,target_train,target_test = \
    train_test_split(data,target,test_size=0.2,random_state=42)

#训练回归树
from sklearn.tree import DecisionTreeClassifier
dtr=DecisionTreeClassifier(criterion='gini',max_depth=8,random_state=42)
dtr.fit(data_train,target_train)

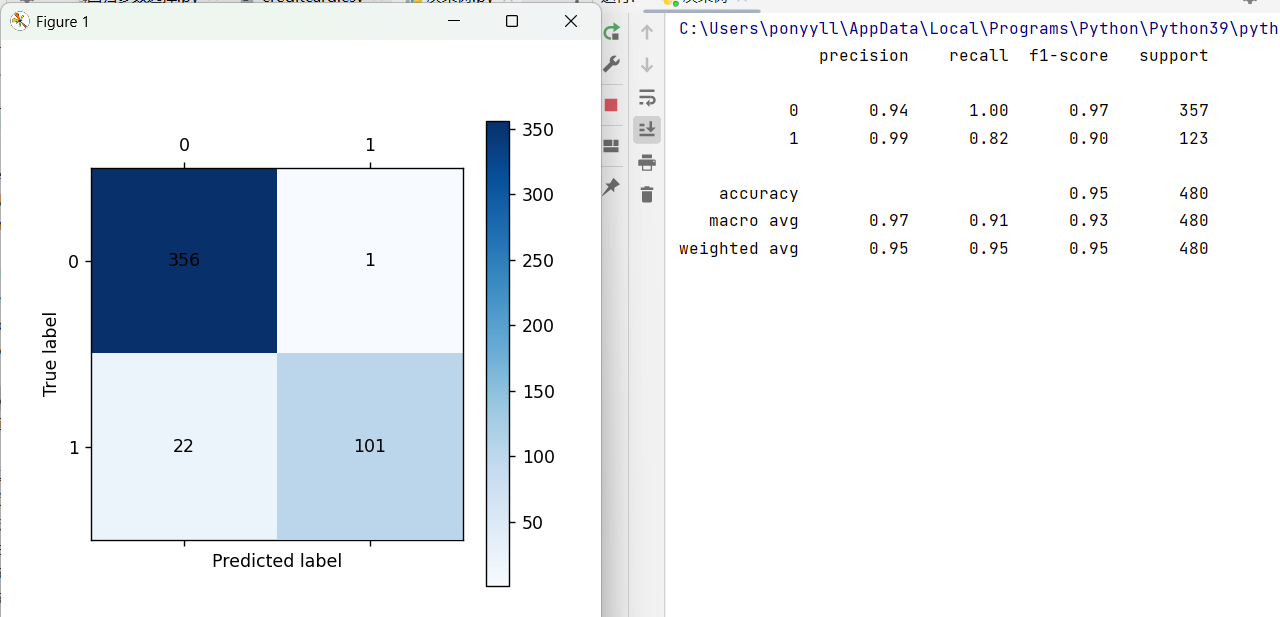
#训练集自测准确率
train_pred = dtr.predict(data_train)
print(metrics.classification_report(target_train,train_pred))
cm_plot(target_train,train_pred).show()

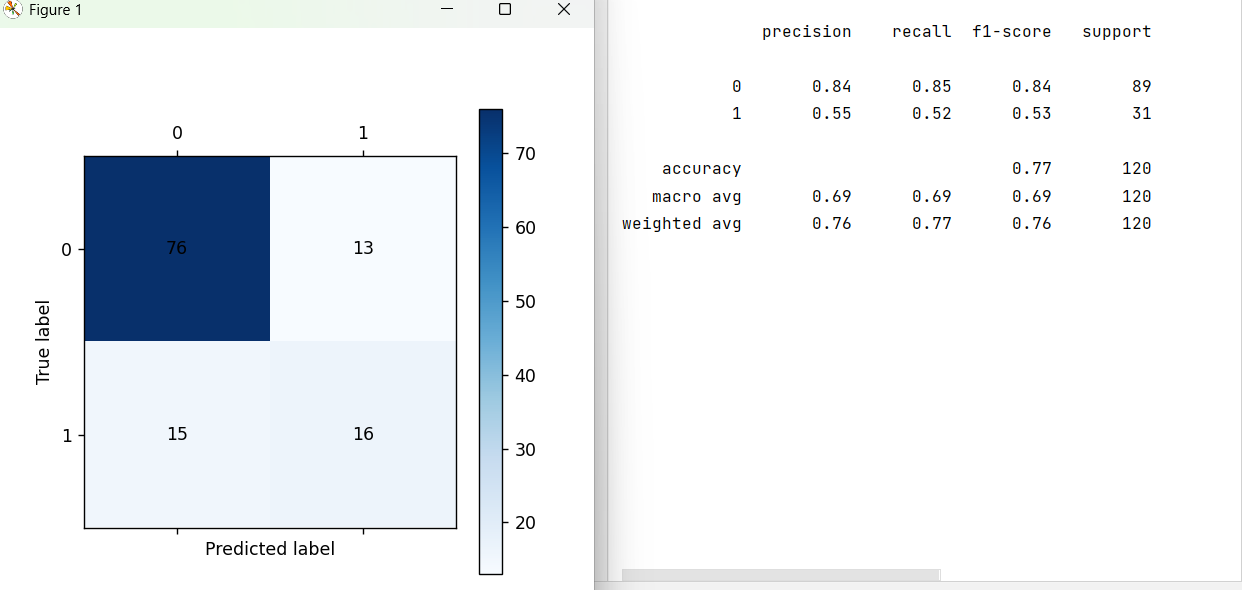
#测试集测试准确率
test_pred = dtr.predict(data_test)
print(metrics.classification_report(target_test,test_pred))
cm_plot(target_test,test_pred).show()

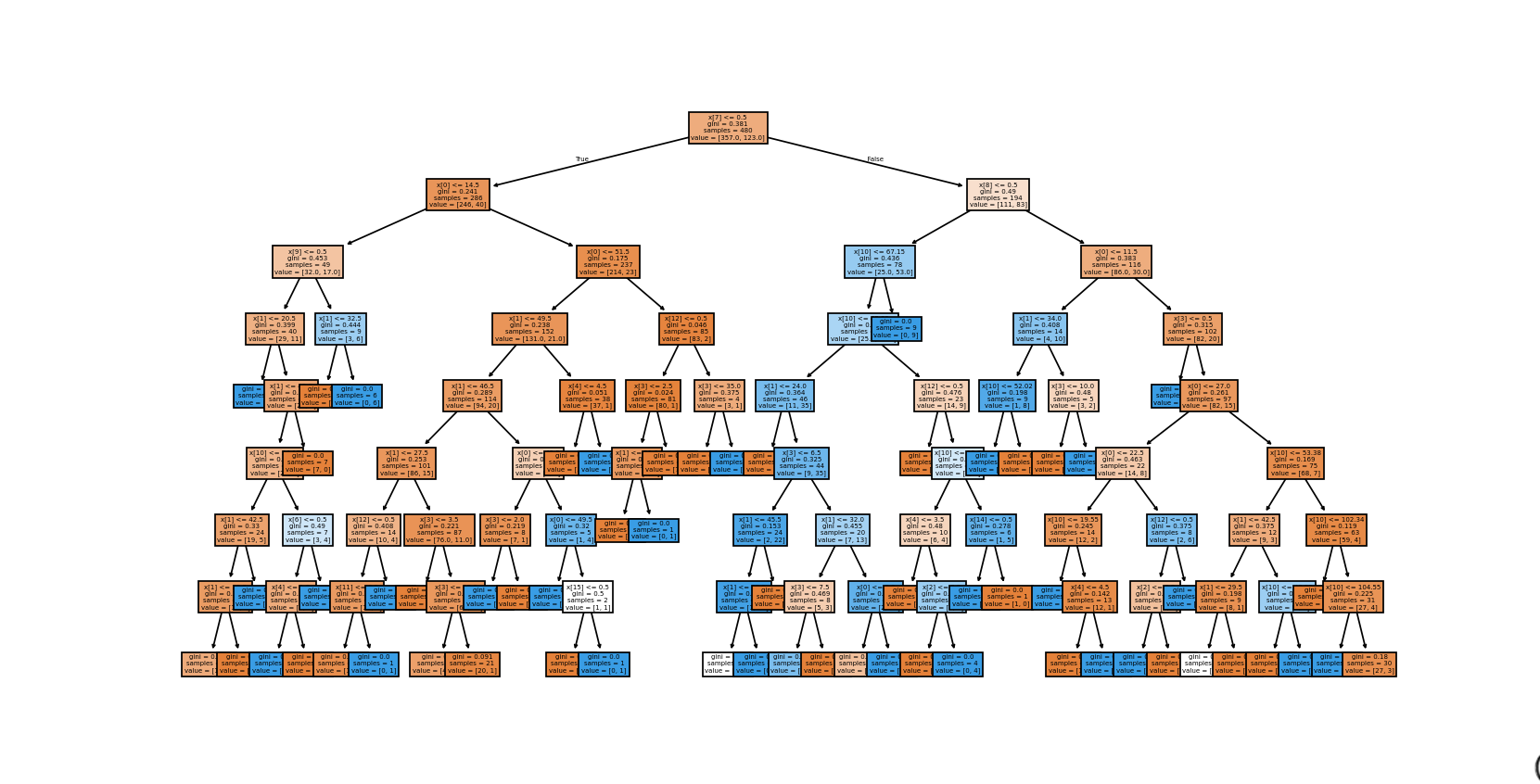
#绘制回归树
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
fig,ax = plt.subplots(figsize=(32,32))
plot_tree(dtr,filled=True,ax=ax)
plt.show()

演示结果：

训练集

测试集

回归树