算法——递归

目录

汉诺塔问题

合并两个有序链表

反转链表

两两交换链表中的节点

[Pow(x, n)](#Pow(x, n))

汉诺塔问题

思路：

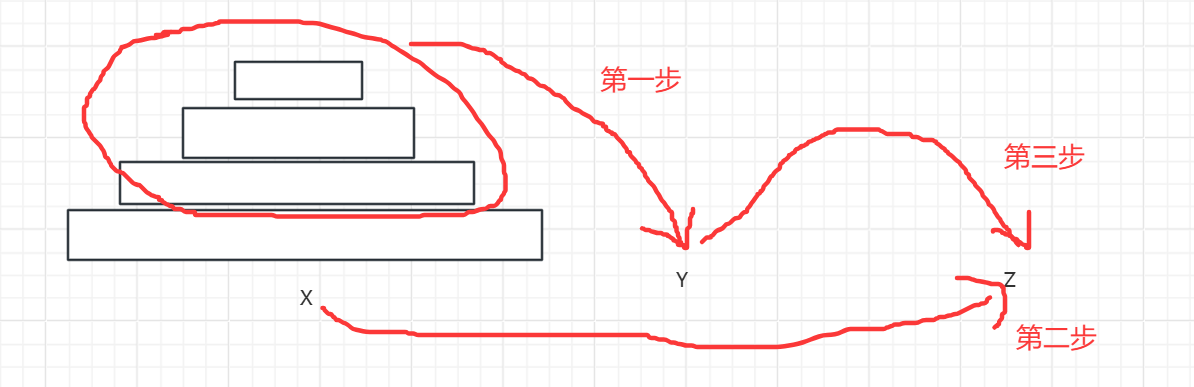
结合上图，我们可以定义一个函数，假设函数头为 dfs (x, y, z, n)，这个函数的作用是将 x 柱子上的 n 个盘子，借助 y 柱子，转移到 z 柱子上面，那么上图整个流程可以表示如下：（假设图中x柱子上一共 n 个盘子）

1. dfs (x, z, y, n - 1)：将 x 柱子上面的 n - 1 个盘子借助 z 柱子，移动到 y 柱子上。
2. x.back() --> z：将 x 柱子上最下面的那个盘子直接移动到 z 柱子上。
3. dfs (y, x, z, n - 1)：将 y 柱子上剩余的 n - 1 个盘子借助 x 移动到 z 上。

递归出口：当只剩下一个盘子（即 n = 1）时，就无需再借助其他柱子移动了，直接移动到目标柱子上即可。

代码：

class Solution {
public:
    void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {
        dfs(A, B, C, A.size());
    }
    void dfs(vector<int>& A, vector<int>& B, vector<int>& C, int n){
        if(n == 1){
            C.push_back(A.back());
            A.pop_back();
            return;
        }

        dfs(A, C, B, n - 1);
        C.push_back(A.back());
        A.pop_back();
        dfs(B, A, C, n - 1);
    }
};

合并两个有序链表

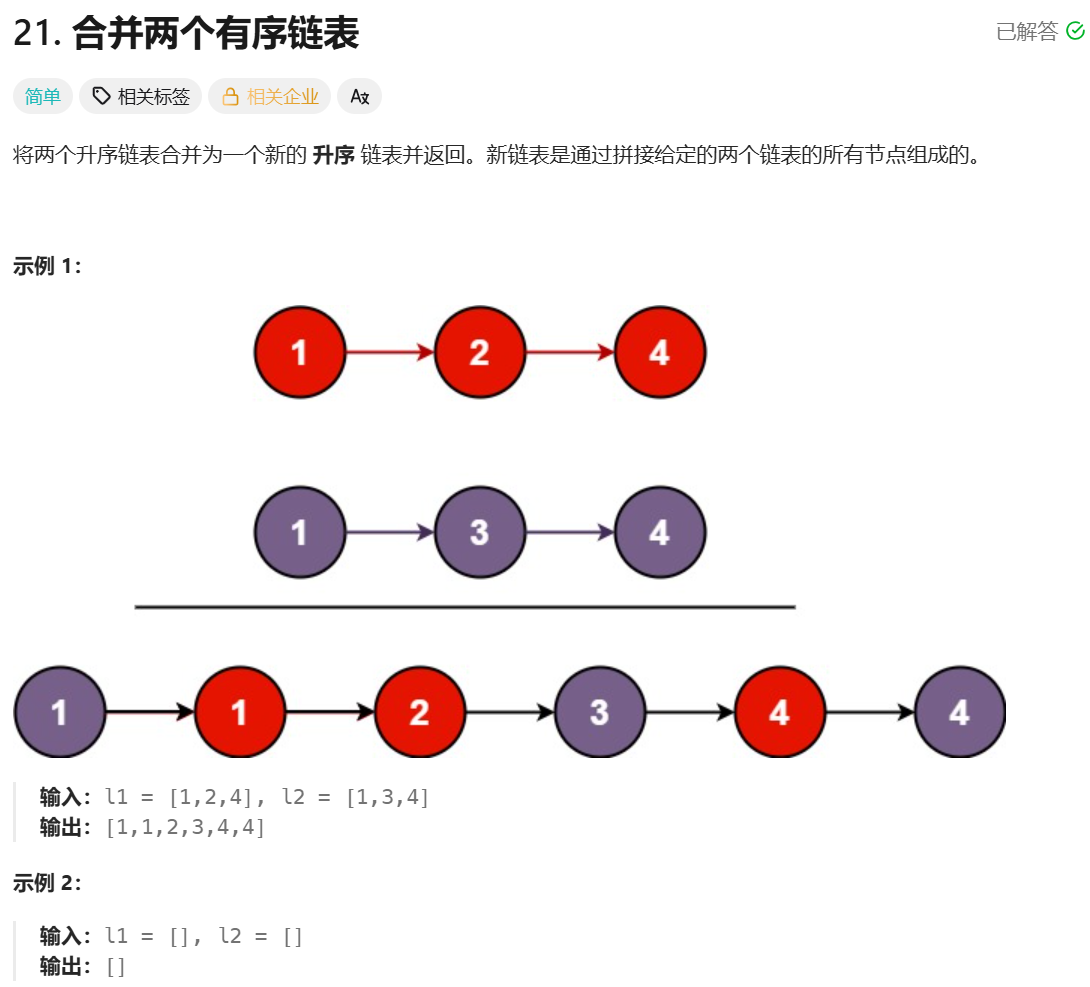
**思路：**合并两个有序链表，本质上就是每次只选当前两个链表头中更小的那个节点，然后让这个节点的next指向 "剩下的两个子链表合并后的结果"。

我们写一个递归函数，作用是合并两个链表，然后模拟上述说的过程即可，先找到小的节点，然后让这个节点的next指向 "剩下的两个子链表合并后的结果"，因为递归函数的作用就是合并链表，所以剩下两个子链表合并的结果只需要去调用一下这个递归函数就可以得到了。

递归函数的出口就是当其中一个链表为空时，直接返回另一个链表，两个都为空时，返回谁都一样。

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution 
{
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) 
    {
        return dfs(list1, list2);    
    }

    ListNode* dfs(ListNode* list1, ListNode* list2)
    {
        if(list1 == NULL)
            return list2;
        if(list2 == NULL)
            return list1;

        if(list1->val < list2->val)
        {
            list1->next = dfs(list1->next, list2);
            return list1;
        }
        else
        {
            list2->next = dfs(list1, list2->next);
            return list2;
        }
    }
};

反转链表

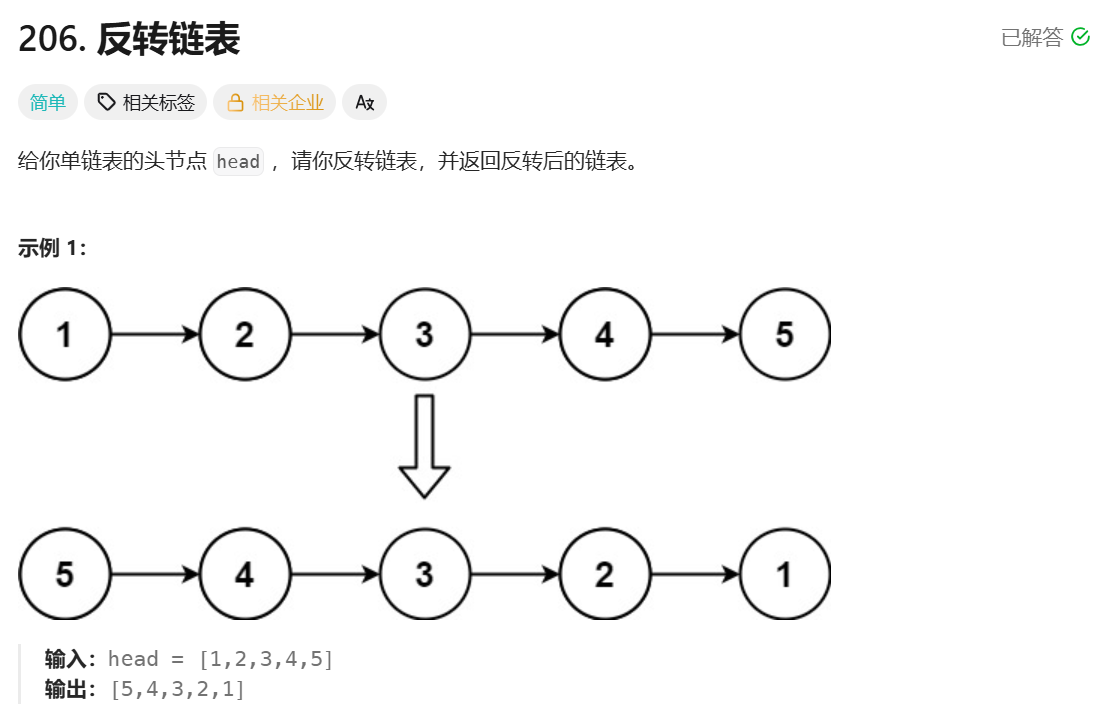
**思路：**要逆序第一个节点，我们可以先逆序第一个节点后面的子链表，逆序好后第一个节点尾插到这个子链表中即可，而逆序第一个节点后面的子链表，又可以先逆序第二个节点后面的子链表，然后把第二个节点尾插到逆序好的链表中，以此类推，这个过程就是递归的过程。

递归出口就是当遇到最后一个节点的时候没有必要逆序了，因为只有这一个节点了，直接返回就行。

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        return dfs(head);
    }

    ListNode* dfs(ListNode* list){
        if(list == NULL || list->next == NULL)
            return list;

        ListNode* node = dfs(list->next);
        ListNode* cur = node;
        while(cur->next){
            cur = cur->next;
        }
        cur->next = list;
        list->next = NULL;

        return node;
    }
};

两两交换链表中的节点

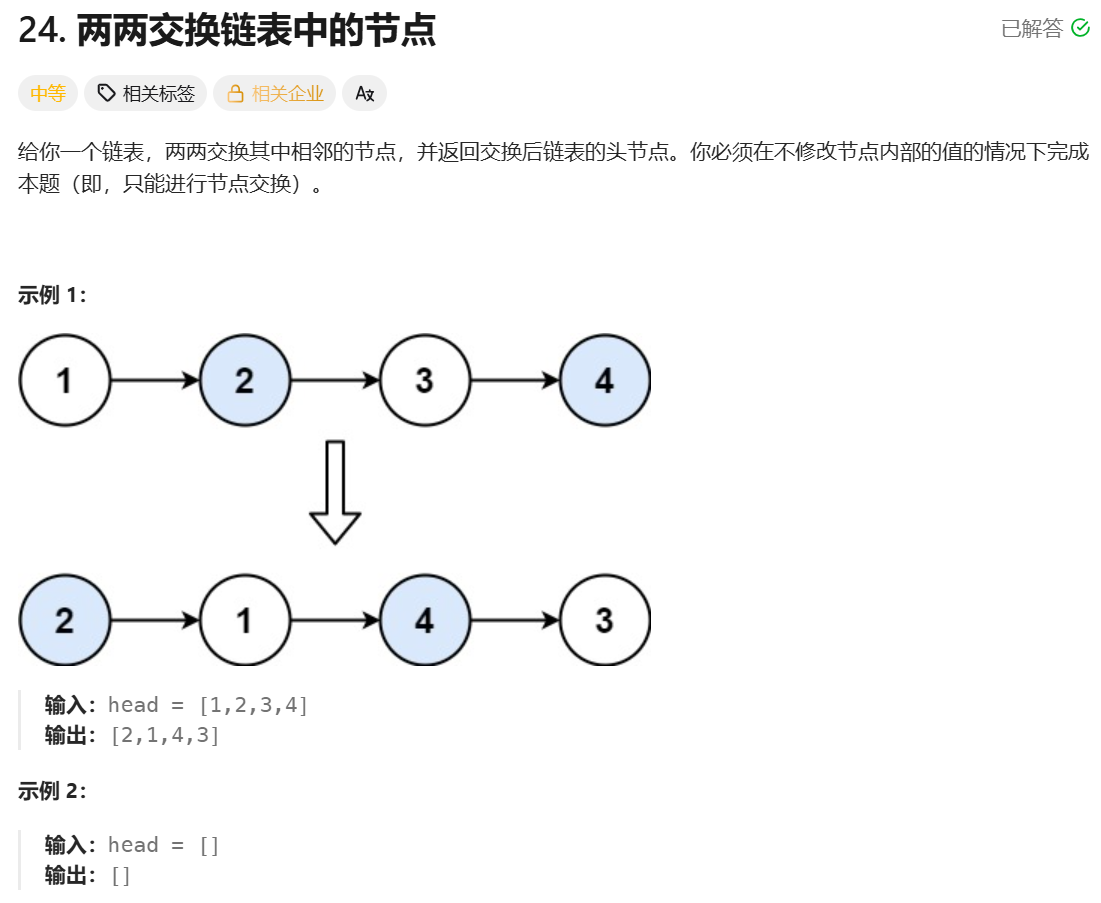
**思路：**要交换前两个节点，我们可以先将后续的链表两两交换好后，再和前两个节点按照题目要求的顺序相连接，后面的节点同理，依次类推，这就是递归的过程。

递归出口就是当只剩下一个节点的时候直接返回，只剩下两个节点的时候交换一下节点的位置然后返回。

代码：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        return dfs(head);
    }

    ListNode* dfs(ListNode* list){
        if(list == NULL || list->next == NULL){
            return list;
        }
        if(list->next->next == NULL){
            ListNode* head = list->next;
            list->next->next = list;
            list->next = NULL;
            return head;
        }

        ListNode* node = dfs(list->next->next);
        ListNode* head = list->next;
        list->next->next = list;
        list->next = node;

        return head;
    }
};

Pow(x, n)

**思路：**计算过程如下图：

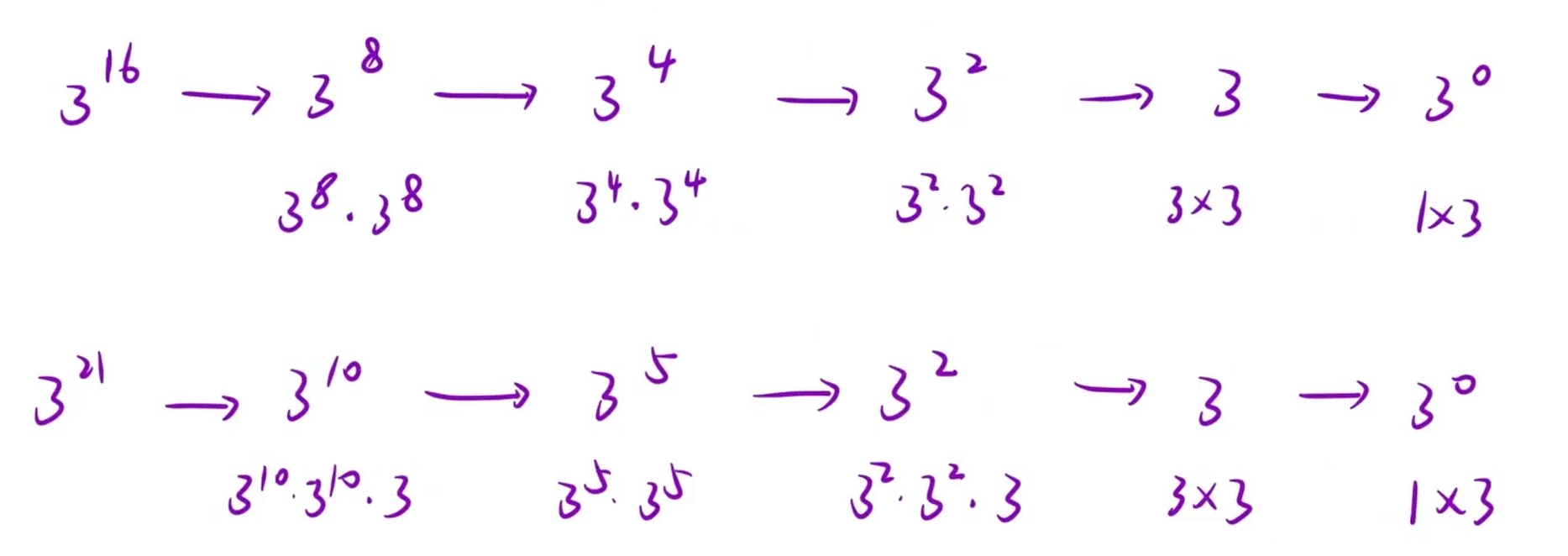
细节问题：

• 这道题 n 可能是负数，如果是负数可以先按正数算，然后再然 1 除以这个数就可以了。
• 当 n 是负数最小值，转换成正数会溢出，所以要强转成 long long。

代码：

class Solution 
{
public:
    double myPow(double x, int n) 
    {
        return n < 0 ? 1.0 / mypow(x, -(long long)n) : mypow(x, n);
    }

    double mypow(double x, long long n)
    {
        if(n == 0)
            return 1.0;

        double ret = mypow(x, n / 2);

        return n % 2 == 0 ? ret * ret : ret * ret * x;
    }
};