例1
cpp
#include<iostream>
#include<vector>
using namespace std;
int n, m;
vector< vector<char>>grid;
int dx[8] = { -1,-1,-1,0,0,1,1,1 };
int dy[8] = { -1,0,1,-1,1,-1,0,1 };
int ans = 0;
void dfs(int x, int y)
{
grid[x][y] = '.';
for (int i = 0; i < 8; i++)
{
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && nx < n && ny >= 0 && ny < m && grid[nx][ny] == 'W')
{
dfs(nx, ny);
}
}
}
int main()
{
cin >> n >> m;
grid.resize(n, vector<char>(m));
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
cin >> grid[i][j];
}
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
if (grid[i][j] == 'W')
{
dfs(i, j);
ans++;
}
}
}
cout << ans;
return 0;
}解析:
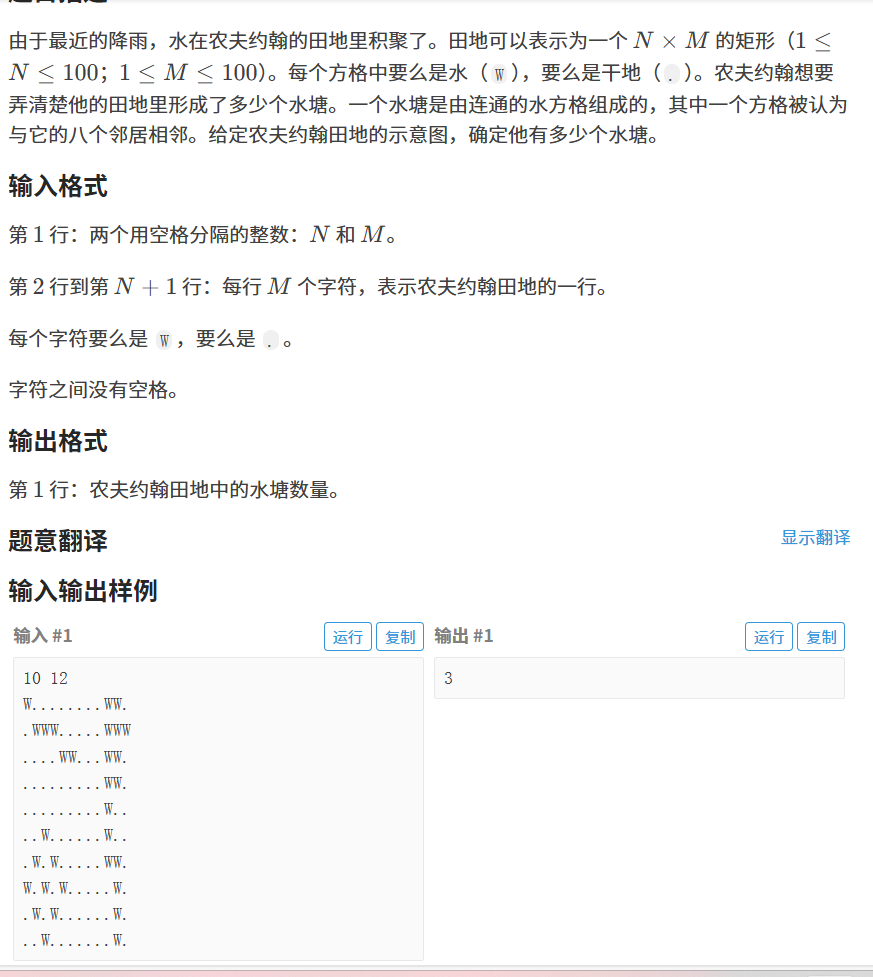
大致思路就是先最开始遍历二维数组(矩形),定义ans记录答案,找到第一个W时,用搜索(广搜或者深搜),将这个W周围所有能到达的W标记为'.',ans++;此时这个W周围所有的湖泊W都被填平了,继续循环,找到第二个W,此时这个W一定和之前那个W是不同的湖泊,因为第一个W周围的湖泊已经被填平了,以此类推,填平第二个W周围湖泊,ans++;
最后输出ans;
-
遍历整个二维数组(田地)
-
找到第一个
W(水) -
用搜索(DFS/BFS) 把这个
W连通的所有W都标记为.(相当于"填平"这个水塘) -
ans++(发现一个完整的水塘)
-
继续遍历 ,因为之前的
W都被填平了,所以新找到的W一定是另一个水塘的 -
重复步骤3-5,直到遍历完整个田地
-
输出 ans
-
你有一个有很多水坑的地面
-
看到一个水坑(第一个
W) -
用一桶水把这个水坑和所有相连的小水坑都填平(标记为
.) -
数:啊,这是一个水塘
-
往前走,又看到一个水坑(肯定和之前那个不相连,不然已经被填平了)
-
再填平,再计数
-
最后数出一共有多少个独立的水塘
例2:
cpp
#include<iostream>
#include<vector>
using namespace std;
int n, m, t;
int sx, sy, fx, fy;
int dx[4] = { -1,0,0,1 };
int dy[4] = { 0,-1,1,0 };
vector<vector<bool>>visited;
vector<vector<int>>maze;
int ans = 0;
void dfs(int x, int y)
{
if (x == fx && y == fy)
{
ans++;
return;
}
for (int i = 0; i < 4; i++)
{
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && nx < n && ny >= 0 && ny < m && !visited[nx][ny])
{
visited[nx][ny] = true;
dfs(nx, ny);
visited[nx][ny] = false;
}
}
}
int main()
{
cin >> n >> m >> t;
cin >> sx >> sy >> fx >> fy;
sx--; sy--; fx--; fy--;
visited.resize(n, vector<bool>(m, false));
maze.resize(n, vector<int>(m));
for (int i = 0; i < t; i++)
{
int x, y;
cin >> x >> y;
x--; y--;
visited[x][y] = true;
}
visited[sx][sy] = true;
dfs(sx, sy);
cout << ans;
return 0;
}解析:
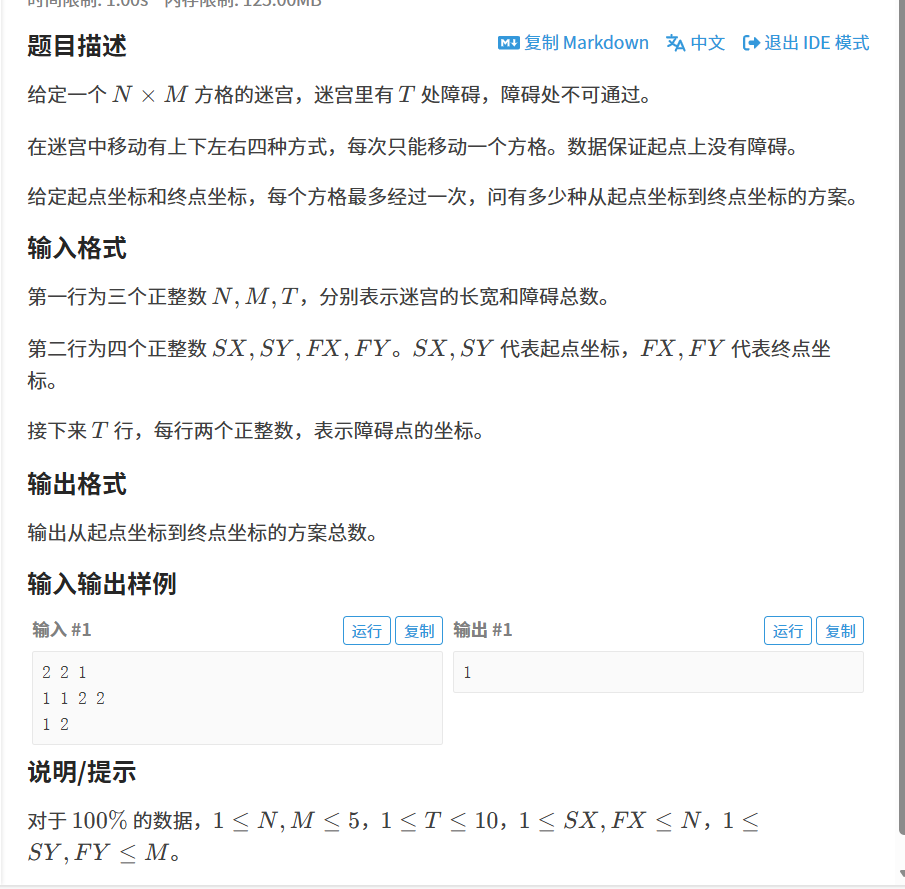
深度优先搜索,从起点开始搜索,起点开始的四个方向,先走一个方向,这个方向再继续向下走,走过的记得标记visited=true,表示已经走过,这次这个路径不会再次走这条路,避免重复,走完之后或者走不通时记得退出来,标记false;
要注意的是这个索引是从1开始的,要是用0开始要给初始值全部减减;
例3:
cpp
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
struct point {
int x, y;
};
int main() {
int n, m, x0, y0, ans[402][402];
int dx[8] = { -1, -2, -2, -1, 1, 2, 2, 1 };
int dy[8] = { -2, -1, 1, 2, -2, -1, 1, 2 };
queue<point> q;
memset(ans, -1, sizeof(ans));
cin >> n >> m >> x0 >> y0;
ans[x0][y0] = 0;
point tp = { x0, y0 }, p;
q.push(tp);
while (!q.empty()) {
tp = q.front();
q.pop();
for (int i = 0; i < 8; i++) {
int x = dx[i] + tp.x, y = dy[i] + tp.y;
if (x < 1 || x > n || y < 1 || y > m || ans[x][y] != -1)
continue;
ans[x][y] = ans[tp.x][tp.y] + 1;
p = { x, y };
q.push(p);
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
cout << ans[i][j] << " ";
}
cout << endl;
}
return 0;
}
cpp
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
int n, m, x, y;
int dx[8] = { -2,-2,2,2,-1,-1,1,1 };
int dy[8] = { -1,1,-1,1,-2,2,-2,2 };
int main()
{
cin >> n >> m >> x >> y;
x--; y--;
vector<vector<int>>arr(n, vector<int>(m, -1));
vector<vector<bool>>visited(n, vector<bool>(m, false));
queue<pair<int, int>>q;
visited[x][y] = true;
arr[x][y] = 0;
q.push({ x,y });
while (!q.empty())
{
int x = q.front().first;
int y = q.front().second;
q.pop();
for (int i = 0; i < 8; i++)
{
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && nx < n && ny >= 0 && ny < m && !visited[nx][ny])
{
arr[nx][ny] = arr[x][y] + 1;
q.push({ nx,ny });
visited[nx][ny] = true;
}
}
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < m; j++)
{
cout << arr[i][j] << " ";
}
cout << endl;
}
return 0;
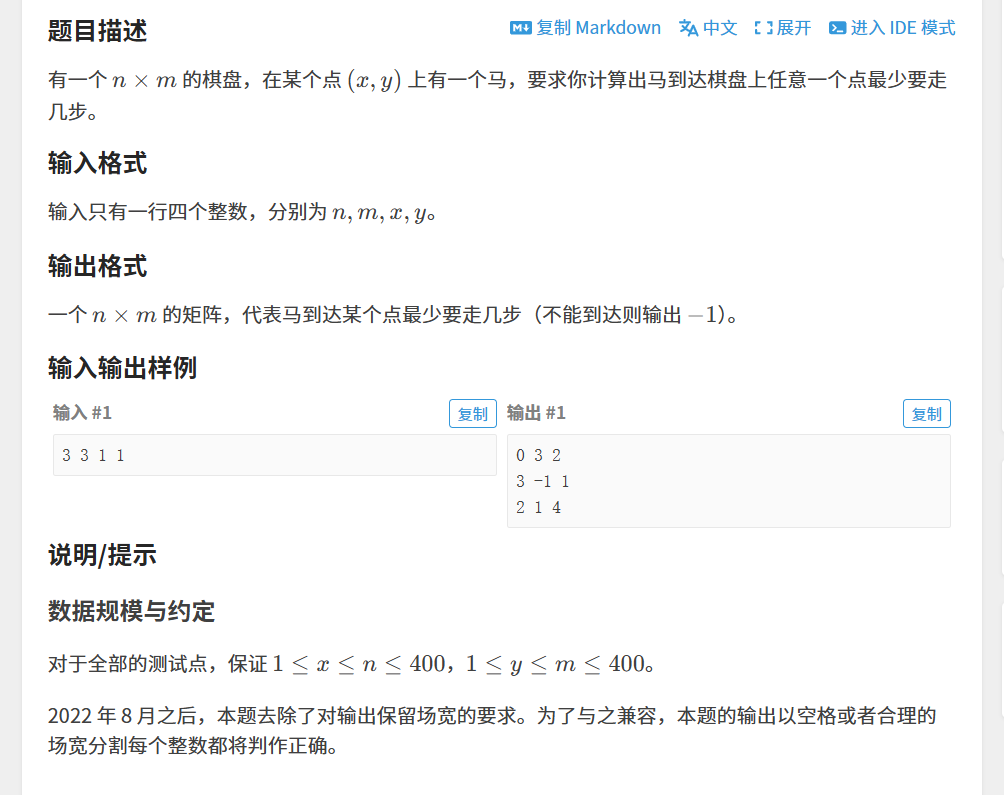
}解析:
广度优先搜索,求最短路径这种用广度优先搜索,本题从x,y开始,广度搜索区别于深度的就是,广度是像水波一样,不断往外蔓延,先走这一圈,这个点能到达的所有点,储存在队列中,然后等把这个点能到达的所有点经历完之后,开始走这个点周围的点,也就是队列里面储存的,所以还要记得走完这个点要删除