1 题目
给你二叉树的根结点 root ,请你将它展开为一个单链表:
- 展开后的单链表应该同样使用
TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null。 - 展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例 1:
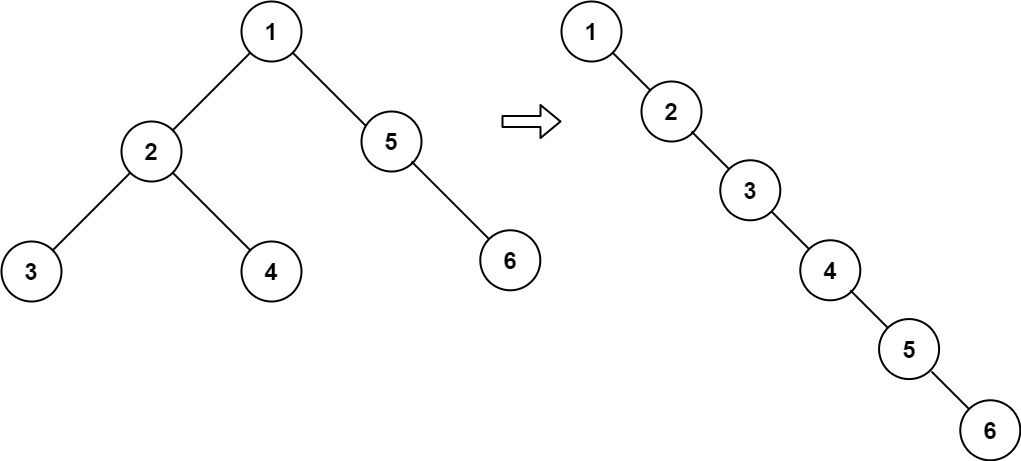
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]示例 2:
输入:root = []
输出:[]示例 3:
输入:root = [0]
输出:[0]提示:
- 树中结点数在范围
[0, 2000]内 -100 <= Node.val <= 100
进阶: 你可以使用原地算法(O(1) 额外空间)展开这棵树吗?
2 代码实现
c++
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void flatten(TreeNode* root) {
if (root == nullptr){
return ;
}
TreeNode* temp = root -> right ;
root -> right = root -> left ;
root -> left = nullptr ;
TreeNode* cur = root ;
while (cur-> right != nullptr){
cur = cur -> right ;
}
cur -> right = temp ;
flatten(root -> left );
flatten(root -> right );
}
};js
javascript
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {void} Do not return anything, modify root in-place instead.
*/
var flatten = function(root) {
if (root == null){
return ;
}
flatten (root.left);
flatten (root.right);
let temp = root.right ;
root.right = root.left ;
root.left = null ;
let cur = root ;
while(cur.right != null){
cur = cur.right;
}
cur.right = temp ;
};思考
递归,怎么做?主要是null要怎么连起来?
自己乱写又出错
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void flatten(TreeNode* root) {
if (root == nullptr){
return ;
}
flatten(root -> left );
flatten(root -> right );
}
};题解
你想要用递归的方式解决二叉树展开为链表的问题,核心是要把二叉树按照先序遍历的顺序,将所有节点通过 right 指针串联起来,同时把 left 指针置为空。你现在的递归框架只做了遍历,但还没有处理节点的指针指向,这就是代码没有实现功能的原因。
递归解法思路
递归解决这个问题的核心思路是后序处理(先处理左子树、再处理右子树、最后处理当前节点):
- 递归展开左子树和右子树;
- 把当前节点的右子树暂存起来,将展开后的左子树接到当前节点的右指针上;
- 将当前节点的左指针置为空;
- 找到当前节点右子树的最后一个节点,把暂存的右子树接到这个最后节点的右指针上。
完整的递归实现代码
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void flatten(TreeNode* root) {
// 递归终止条件:空节点直接返回
if (root == nullptr) {
return;
}
// 1. 递归展开左子树和右子树
flatten(root->left);
flatten(root->right);
// 2. 暂存原来的右子树
TreeNode* temp_right = root->right;
// 3. 将展开后的左子树移到右子树位置,左子树置空
root->right = root->left;
root->left = nullptr;
// 4. 找到当前右子树(原左子树)的最后一个节点
TreeNode* curr = root;
while (curr->right != nullptr) {
curr = curr->right;
}
// 5. 将暂存的右子树接到最后一个节点的右指针上
curr->right = temp_right;
}
};代码关键部分解释
- 递归终止条件 :当节点为
nullptr时,无需处理,直接返回,这是递归的基础。 - 递归处理子树:先递归展开左、右子树,保证子树已经是符合要求的单链表结构。
- 暂存右子树:因为要把左子树移到右子树位置,必须先保存原来的右子树,否则会丢失。
- 左子树迁移与置空 :把展开后的左子树赋值给
root->right,同时将root->left置为null,满足题目 "左子指针始终为 null" 的要求。 - 拼接原右子树 :遍历当前的右子树(原左子树)找到最后一个节点,把暂存的原右子树接到这个节点的
right上,完成整个链表的拼接。
测试示例(以示例 1 为例)
输入:root = [1,2,5,3,4,null,6]执行过程关键步骤:
- 先递归处理节点 2 的左子树 3、右子树 4,将 2 的左子树移到右,左置空,此时 2 的结构是
2->3->4(左为 null); - 处理节点 5 的右子树 6,5 的左为 null,直接拼接 6,结构是
5->6; - 回到根节点 1,将左子树(2->3->4)移到右,左置空,再找到 4(当前右子树最后节点),拼接 5->6,最终得到
1->2->3->4->5->6(所有左指针为 null)。
进阶:原地算法(O (1) 空间)
如果想实现进阶要求的 O (1) 额外空间(递归会用到栈空间,空间复杂度 O (n)),可以用莫里斯遍历(Morris Traversal),核心思路是利用二叉树的空闲右指针记录遍历的前驱节点,避免递归栈:
cpp
class Solution {
public:
void flatten(TreeNode* root) {
TreeNode* curr = root;
while (curr != nullptr) {
if (curr->left != nullptr) {
// 找到左子树的最右节点(前驱节点)
TreeNode* predecessor = curr->left;
while (predecessor->right != nullptr) {
predecessor = predecessor->right;
}
// 将当前节点的右子树接到前驱节点的右指针
predecessor->right = curr->right;
// 将左子树移到右子树位置,左置空
curr->right = curr->left;
curr->left = nullptr;
}
// 处理下一个节点
curr = curr->right;
}
}
};总结
- 递归解法的核心是后序处理:先展开子树,再调整当前节点的指针,把左子树移到右、拼接原右子树;
- 必须将所有节点的
left指针置为null,这是题目明确要求; - 进阶的莫里斯遍历可以实现 O (1) 额外空间,核心是利用左子树的最右节点作为前驱,提前拼接右子树。
3 题目
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。
判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
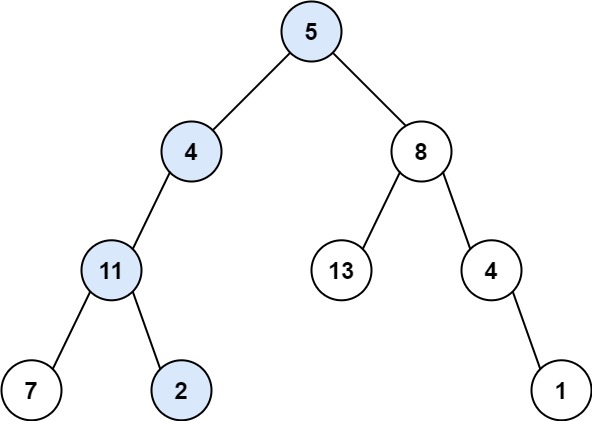
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。示例 2:
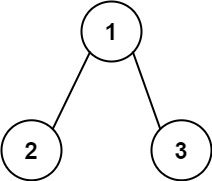
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。提示:
- 树中节点的数目在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
4 代码实现
c++
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == nullptr){
return false ;
}
if (root -> left == nullptr && root -> right == nullptr){
return targetSum == root-> val ;
}
bool left_ok = hasPathSum (root -> left , targetSum - root -> val );
bool right_ok = hasPathSum (root -> right ,targetSum - root -> val );
return left_ok || right_ok ;
}
};js
javascript
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {boolean}
*/
var hasPathSum = function(root, targetSum) {
if (root == null){
return false ;
}
if (root.left == null && root.right == null){
return root.val == targetSum ;
}
let left_ok = hasPathSum (root.left , targetSum - root.val);
let right_ok = hasPathSum (root.right , targetSum - root.val );
return left_ok || right_ok ;
};思考
深度优先搜索,counter计数写一个循环,比较。但是难点在于我不知道深度优先搜索怎么写......
题解
你想要用深度优先搜索(DFS)来解决二叉树的路径总和问题,核心是判断是否存在从根节点到叶子节点的路径,其节点值之和等于目标值 targetSum。DFS 是解决这类路径遍历问题的经典方法,我会先帮你理解 DFS 的核心思路,再给出清晰的代码实现。
DFS 解题思路
深度优先搜索的核心是递归遍历二叉树的每一条从根到叶子的路径,在遍历过程中累加节点值:
- 递归终止条件 :
- 如果当前节点是
nullptr,直接返回false(空路径不可能满足条件); - 如果当前节点是叶子节点(左右子节点都为
nullptr),判断当前累加和是否等于targetSum。
- 如果当前节点是
- 递归过程 :
- 从根节点开始,每访问一个节点,就用
targetSum减去当前节点的值(等价于累加路径和,这样可以避免额外的变量); - 递归检查左子树和右子树,只要其中一条路径满足条件,就返回
true。
- 从根节点开始,每访问一个节点,就用
完整的 DFS 实现代码
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
// 终止条件1:空树,直接返回false
if (root == nullptr) {
return false;
}
// 终止条件2:当前是叶子节点,判断剩余目标和是否等于当前节点值
if (root->left == nullptr && root->right == nullptr) {
return targetSum == root->val;
}
// 递归处理左子树和右子树:
// 把targetSum减去当前节点值,传递给子节点
// 只要左/右子树有一个满足条件,就返回true
bool left_ok = hasPathSum(root->left, targetSum - root->val);
bool right_ok = hasPathSum(root->right, targetSum - root->val);
return left_ok || right_ok;
}
};代码关键部分解释
- 空节点处理 :如果传入的节点是
nullptr,说明这条路径走不通,直接返回false,这是递归的基础终止条件。 - 叶子节点判断 :叶子节点的定义是 "没有子节点"(
left和right都为nullptr),此时只需判断 "剩余的目标和" 是否等于当前节点值(因为前面的路径和已经用targetSum - 父节点值抵消了)。 - 递归传递剩余目标和 :每往下走一层,就用
targetSum减去当前节点的值,相当于 "累计路径和" 的反向操作(比如目标和是 22,根节点是 5,那么子节点需要凑的和就是 17)。 - 逻辑或判断 :左子树或右子树只要有一条路径满足条件,整体就满足,因此返回
left_ok || right_ok。
测试示例(以示例 1 为例)
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1],targetSum = 22执行过程关键步骤:
- 根节点 5:剩余目标和 = 22 - 5 = 17,递归检查左子树(4);
- 节点 4:剩余目标和 = 17 - 4 = 13,递归检查左子树(11);
- 节点 11:剩余目标和 = 13 - 11 = 2,递归检查左子树(7)→ 7 是叶子,2≠7 → false;检查右子树(2)→ 2 是叶子,2=2 → true;
- 最终返回
true,符合示例 1 的结果。
非递归 DFS 实现(栈模拟,可选)
如果你想理解 DFS 的非递归写法(避免递归栈溢出),可以用栈来模拟递归过程,思路是同时保存 "当前节点" 和 "到当前节点的路径和":
cpp
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if (root == nullptr) return false;
// 栈中保存<当前节点, 到当前节点的路径和>
stack<pair<TreeNode*, int>> st;
st.push({root, root->val});
while (!st.empty()) {
auto [curr, sum] = st.top();
st.pop();
// 叶子节点,判断路径和是否等于目标
if (curr->left == nullptr && curr->right == nullptr) {
if (sum == targetSum) return true;
continue;
}
// 先压右子树(栈是后进先出,保证先遍历左子树)
if (curr->right != nullptr) {
st.push({curr->right, sum + curr->right->val});
}
// 再压左子树
if (curr->left != nullptr) {
st.push({curr->left, sum + curr->left->val});
}
}
return false;
}
};总结
- 递归 DFS 解决路径总和的核心是减治思想:每访问一个节点就用目标和减去节点值,直到叶子节点判断是否匹配;(这个我没想到,我以为要顺着思路拿来加,其实减更巧妙)
- 必须严格判断 "叶子节点"(左右子节点都为空),不能只判断单个子节点为空,否则会误判非叶子节点;
- 递归写法简洁易懂,是解决二叉树路径问题的首选,非递归写法(栈)则更适合处理节点数极多的情况。
js写为什么错
javascript
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {boolean}
*/
var hasPathSum = function(root, targetSum) {
if (root == null){
return false ;
}
if (root.left == null && root.right == null){
return root == targetSum ;
}
let left_ok = hasPathSum (root.left , targetSum - root.val);
let right_ok = hasPathSum (root.right , targetSum - root.val );
return left_ok || right_ok ;
};错误原因分析
你代码中最关键的错误在叶子节点的判断行:
return root == targetSum ; // 错误!这里你把整个节点对象 root 和目标值 targetSum 做比较,而正确的应该是比较节点的值 root.val 和剩余的目标和。
5 小结
学习到了新知识: DFS减治思想,还有感受下递归,二叉树这块很重要。