【C++】深入浅出“图”——最短路径算法

文章目录

一、Dijkstra算法
二、Bellman_Ford算法
三、Floyd_Warshall算法

一、Dijkstra算法

最短路径问题是指，从在带权的有向图中从某一顶点出发，找到通往另一顶点的最短路径，"最短"指的是沿路径各边的权值总和最小。

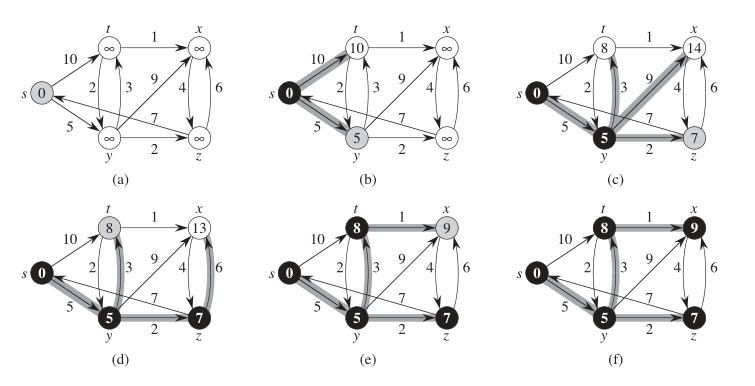
Dijkstra算法是单源最短路径的经典贪心算法，只能用于没有负权的图 。它从起点出发，每次选当前距离最小且未确定最短路径的节点，用它去松弛（更新）所有邻接点的最短路径估计值，标记该节点为 "已确定"，重复此过程直到所有节点处理完毕，最终得到起点到图中所有节点的最短路径。

cpp 复制代码

// src是选定的起点，dist记录起点到各点的最短路径，pPath记录到每个点的最短路径的前驱顶点下标
void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{
		size_t srci = GetVertexIndex(src);
		size_t n = _vertexs.size();
		dist.resize(n, MAX_W);
		pPath.resize(n, -1);

		dist[srci] = 0;
		pPath[srci] = srci;

		// 已经确定最短路径的顶点集合
		vector<bool> S(n, false);

		for (size_t j = 0; j < n; ++j)
		{
			// 选最短路径顶点且不在S更新其他路径
			int u = 0;
			W min = MAX_W;
			for (size_t i = 0; i < n; ++i)
			{
				if (S[i] == false && dist[i] < min)
				{
					u = i;
					min = dist[i];
				}
			}

			S[u] = true;
			// 松弛更新u连接顶点v  srci->u + u->v <  srci->v  更新
			for (size_t v = 0; v < n; ++v)
			{
				if (S[v] == false && _matrix[u][v] != MAX_W
					&& dist[u] + _matrix[u][v] < dist[v])
				{
					dist[v] = dist[u] + _matrix[u][v];
					pPath[v] = u;
				}
			}
		}
}

二、Bellman_Ford算法

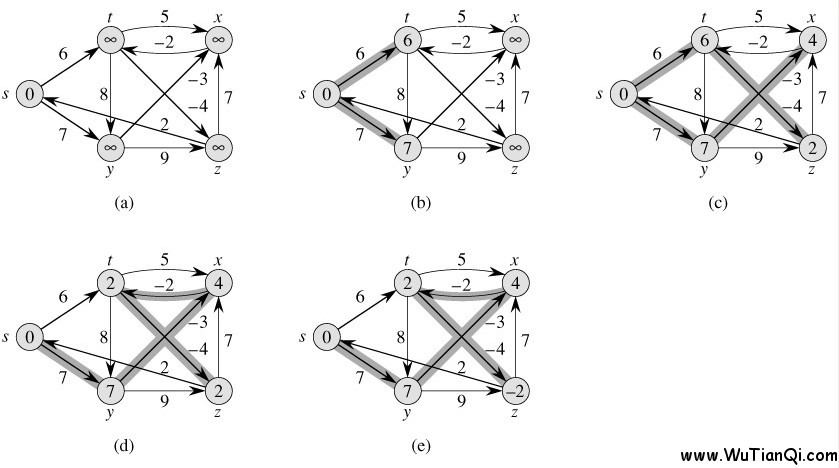
Bellman_Ford算法能用来解决负权图的单源最短路径问题，但是它的时间复杂度高于Dijkstra算法，本质是暴力求解。从起点出发，把图里所有边从头到尾松弛一遍，重复n次，就能算出起点到所有点的最短路径；因为任何最短路径最多只经过n‑1条边。跑完之后再扫一遍所有边，如果还能更新距离，就说明图里有负权回路，最短路径不存在。

cpp 复制代码

bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath)
{
		size_t n = _vertexs.size();
		size_t srci = GetVertexIndex(src);

		// vector<W> dist,记录srci-其他顶点最短路径权值数组
		dist.resize(n, MAX_W);

		// vector<int> pPath 记录srci-其他顶点最短路径父顶点数组
		pPath.resize(n, -1);

		// 先更新srci->srci为缺省值
		dist[srci] = W();

		// 总体最多更新n轮
		for (size_t k = 0; k < n; ++k)
		{
			// i->j 更新松弛
			bool update = false;
			cout << "更新第:" << k << "轮" << endl;
			for (size_t i = 0; i < n; ++i)
			{
				for (size_t j = 0; j < n; ++j)
				{
					// srci -> i + i ->j
					if (_matrix[i][j] != MAX_W && dist[i] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
	 			    {
						update = true;
						//cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << endl;
						dist[j] = dist[i] + _matrix[i][j];
						pPath[j] = i;
					}
				}
			}

			// 如果这个轮次中没有更新出更短路径，那么后续轮次就不需要再走了
			if (update == false)
			{
				break;
			}
		}

		// 还能更新就是带负权回路
		for (size_t i = 0; i < n; ++i)
		{
			for (size_t j = 0; j < n; ++j)
			{
				// srci -> i + i ->j
				if (_matrix[i][j] != MAX_W && dist[i] + _matrix[i][j] < dist[j])
				{
					return false;
				}
			}
		}

		return true;
}

三、Floyd_Warshall算法

Floyd-Warshall算法是求任意两点之间最短路径的算法，依次把每个点当作中转点，判断从 i 到 j 是直接走更近，还是经过这个中转点 k 再走更近，不断更新所有点对的最短距离，三层循环跑完就得到全图最短路径。

cpp 复制代码

void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
{
		size_t n = _vertexs.size();
		vvDist.resize(n);
		vvpPath.resize(n);

		// 初始化权值和路径矩阵
		for (size_t i = 0; i < n; ++i)
		{
			vvDist[i].resize(n, MAX_W);
			vvpPath[i].resize(n, -1);
		}

		// 直接相连的边更新一下
		for (size_t i = 0; i < n; ++i)
		{
			for (size_t j = 0; j < n; ++j)
			{
				if (_matrix[i][j] != MAX_W)
				{
					vvDist[i][j] = _matrix[i][j];
					vvpPath[i][j] = i;
				}
				if (i == j)
				{
					vvDist[i][j] = W();
				}
			}
		}

		// 最短路径的更新i-> {其他顶点} ->j
		for (size_t k = 0; k < n; ++k)
		{
			for (size_t i = 0; i < n; ++i)
			{
				for (size_t j = 0; j < n; ++j)
				{
					// k 作为的中间点尝试去更新i->j的路径
					if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W
							&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j])
					{
						vvDist[i][j] = vvDist[i][k] + vvDist[k][j];
							// 找跟j相连的上一个邻接顶点
							// 如果k->j 直接相连，上一个点就k，vvpPath[k][j]存就是k
							// 如果k->j 没有直接相连，k->...->x->j，vvpPath[k][j]存就是x
						vvpPath[i][j] = vvpPath[k][j];
					}
				}
			}

		}	
}