基于分解的多目标进化算法（MOEA/D）求解46个多目标函数及一个工程应用，包含四种评价指标，MATLAB代码

基于分解的多目标进化算法（Multiobjective Evolutionary Algorithm Based on Decomposition，MOEA/D）是2007年 提出的经典多目标进化算法。它的核心是将多目标优化问题（MOP）分解为一组单目标子问题，通过进化算法协同优化这些子问题，最终逼近Pareto最优前沿 。相比NSGA‑II等基于Pareto支配的算法，MOEA/D在高维多目标优化、解的分布性、计算效率上优势显著。

---

一、核心背景与问题定义

1. 多目标优化问题（MOP）

一般形式：
minimize f ( x ) = ( f 1 ( x ) , f 2 ( x ) , ... , f m ( x ) ) T subject to x ∈ Ω \begin{align*} \text{minimize} \quad & \mathbf{f}(\mathbf{x}) = (f_1(\mathbf{x}), f_2(\mathbf{x}), \dots, f_m(\mathbf{x}))^T \\ \text{subject to} \quad & \mathbf{x} \in \Omega \end{align*} minimizesubject tof(x)=(f1(x),f2(x),...,fm(x))Tx∈Ω

• x \mathbf{x} x：决策向量， Ω \Omega Ω为决策空间；
• f 1 , ... , f m f_1,\dots,f_m f1,...,fm：m个相互冲突的目标函数；
• 目标：找到一组Pareto最优解（无法在不恶化至少一个目标的前提下改进其他目标）。

2. MOEA/D的核心思想

将MOP分解为N个单目标子问题 ，每个子问题对应一个权重向量 λ \lambda λ ，代表不同的偏好方向；通过邻域协作同时优化所有子问题，最终得到均匀覆盖Pareto前沿的解集。

---

二、关键技术模块

1. 分解策略（核心）

将多目标函数通过标量化函数转化为单目标子问题，常用3种方法：

（1）加权和法（Weighted Sum, WS）

g W S ( x ∣ λ ) = ∑ i = 1 m λ i f i ( x ) g^{WS}(\mathbf{x}|\lambda) = \sum_{i=1}^m \lambda_i f_i(\mathbf{x}) gWS(x∣λ)=i=1∑mλifi(x)

• λ i ≥ 0 \lambda_i \ge 0 λi≥0， ∑ i = 1 m λ i = 1 \sum_{i=1}^m \lambda_i=1 ∑i=1mλi=1；
• 优点：简单高效；缺点：无法处理非凸Pareto前沿。

（2）切比雪夫法（Tchebycheff, TCH）

g T C H ( x ∣ λ , z ∗ ) = max ⁡ 1 ≤ i ≤ m { λ i ∣ f i ( x ) − z i ∗ ∣ } g^{TCH}(\mathbf{x}|\lambda, \mathbf{z}^*) = \max_{1 \le i \le m} \left\{ \lambda_i |f_i(\mathbf{x}) - z_i^*| \right\} gTCH(x∣λ,z∗)=1≤i≤mmax{λi∣fi(x)−zi∗∣}

• z ∗ = ( z 1 ∗ , ... , z m ∗ ) \mathbf{z}^*=(z_1^*,\dots,z_m^*) z∗=(z1∗,...,zm∗)：理想点（各目标单独最优值）；
• 优点：可处理凸/非凸前沿，是MOEA/D最常用方法。

（3）边界交集法（Boundary Intersection, BI）

g B I ( x ∣ λ , z ∗ ) = d 1 + θ d 2 g^{BI}(\mathbf{x}|\lambda, \mathbf{z}^*) = d_1 + \theta d_2 gBI(x∣λ,z∗)=d1+θd2

• d 1 d_1 d1：解到权重方向的垂直距离； d 2 d_2 d2：沿权重方向到理想点的距离；
• 优点：对前沿形状适应性更强，计算稍复杂。

2. 权重向量生成

为N个子问题生成均匀分布 的权重向量 λ 1 , ... , λ N \lambda^1,\dots,\lambda^N λ1,...,λN，保证解在Pareto前沿均匀分布。

• 常用方法：均匀设计、单纯格点法；
• 例：m=2目标时， λ = ( t , 1 − t ) , t = 0 , 1 / N , 2 / N , ... , 1 \lambda=(t,1-t), t=0,1/N,2/N,\dots,1 λ=(t,1−t),t=0,1/N,2/N,...,1。

3. 邻域结构

每个子问题 i i i定义邻域 B ( i ) B(i) B(i)（包含T个最邻近的权重向量对应的子问题），仅在邻域内交换信息：

• 作用：控制搜索范围、保持种群多样性、降低计算复杂度；
• 邻域大小T：一般取10--30，T越大全局搜索越强，越小局部搜索越精细。

4. 进化操作（以DE为例）

（1）选择

从子问题 i i i的邻域 B ( i ) B(i) B(i)中随机选3个父代解 x r 1 , x r 2 , x r 3 \mathbf{x}{r1},\mathbf{x}{r2},\mathbf{x}_{r3} xr1,xr2,xr3。

（2）交叉（差分进化DE）

v = x r 1 + F ⋅ ( x r 2 − x r 3 ) \mathbf{v} = \mathbf{x}{r1} + F \cdot (\mathbf{x}{r2} - \mathbf{x}_{r3}) v=xr1+F⋅(xr2−xr3)

• F F F：缩放因子（0.5--1）； v \mathbf{v} v为试验向量。

（3）变异

对 v \mathbf{v} v执行多项式变异，生成子代 y \mathbf{y} y。

（4）更新

用子代 y \mathbf{y} y更新邻域内所有子问题的解 ：若 y \mathbf{y} y在子问题 j j j的标量化函数上更优，则替换 x j \mathbf{x}_j xj为 y \mathbf{y} y。

5. 目标归一化

处理目标量纲/尺度差异：
f i ′ ( x ) = f i ( x ) − z i ∗ z i n a d − z i ∗ f_i'(\mathbf{x}) = \frac{f_i(\mathbf{x}) - z_i^*}{z_i^{nad} - z_i^*} fi′(x)=zinad−zi∗fi(x)−zi∗

• z i n a d z_i^{nad} zinad：最低点（各目标在当前种群的最差值）；
• 归一化后所有目标映射到[0,1]，保证权重公平性。

6. 外部种群（EP）

可选：存储所有非支配解，用于输出最终解集，不参与进化过程。

---

三、MOEA/D完整算法流程

1. 初始化

   • 生成N个均匀权重向量 λ 1 , ... , λ N \lambda^1,\dots,\lambda^N λ1,...,λN；
   • 初始化种群 X = { x 1 , ... , x N } \mathbf{X}=\{\mathbf{x}_1,\dots,\mathbf{x}_N\} X={x1,...,xN}，计算目标值 f ( x i ) \mathbf{f}(\mathbf{x}_i) f(xi)；
   • 计算理想点 z ∗ \mathbf{z}^* z∗，构建每个子问题的邻域 B ( i ) B(i) B(i)；
   • 初始化外部种群EP（可选）。

2. 进化循环（直到满足终止条件）

   • 对每个子问题 i = 1 , ... , N i=1,\dots,N i=1,...,N：
     1. 从邻域 B ( i ) B(i) B(i)选父代，执行交叉、变异，生成子代 y \mathbf{y} y；
     2. 计算 f ( y ) \mathbf{f}(\mathbf{y}) f(y)，更新理想点 z ∗ \mathbf{z}^* z∗；
     3. 邻域更新 ：遍历 B ( i ) B(i) B(i)中所有子问题 j j j，若 g ( y ∣ λ j , z ∗ ) < g ( x j ∣ λ j , z ∗ ) g(\mathbf{y}|\lambda^j,\mathbf{z}^*) < g(\mathbf{x}_j|\lambda^j,\mathbf{z}^*) g(y∣λj,z∗)<g(xj∣λj,z∗)，则 x j = y \mathbf{x}_j = \mathbf{y} xj=y；
     4. 更新外部种群EP（可选）。

3. 输出

   • 输出种群 X \mathbf{X} X或外部种群EP中的非支配解。

---

四、核心优势与特点

1. 计算效率高
   • 适应度计算为标量比较，复杂度 O ( N ) O(N) O(N)；远低于NSGA‑II的 O ( N 2 ) O(N^2) O(N2)（N为种群规模）。
2. 高维适应性强
   • 避免"维度灾难"：高维下Pareto支配几乎失效，而标量化仍能提供有效选择压力。
3. 解分布均匀
   • 权重向量均匀设计+邻域协作，天然保证解集在Pareto前沿均匀分布。
4. 易并行化
   • 子问题间仅邻域交互，可分布式并行求解，大幅提速。
5. 灵活性高
   • 可嵌入任意单目标进化算子（DE、GA、PSO等）；适配多种分解策略。

---

五、与NSGA‑II的核心对比

对比维度	MOEA/D	NSGA‑II
核心思想	分解为单目标子问题，协同优化	基于Pareto支配排序+拥挤度
适应度计算	标量函数值（快速）	非支配排序+拥挤距离（ O ( N 2 ) O(N^2) O(N2)）
高维表现	优秀（选择压力稳定）	差（支配失效、拥挤度失效）
解分布	均匀（权重驱动）	依赖拥挤度，易不均匀
计算复杂度	O ( N ) O(N) O(N)	O ( N 2 ) O(N^2) O(N2)
并行性	易并行	难并行

---

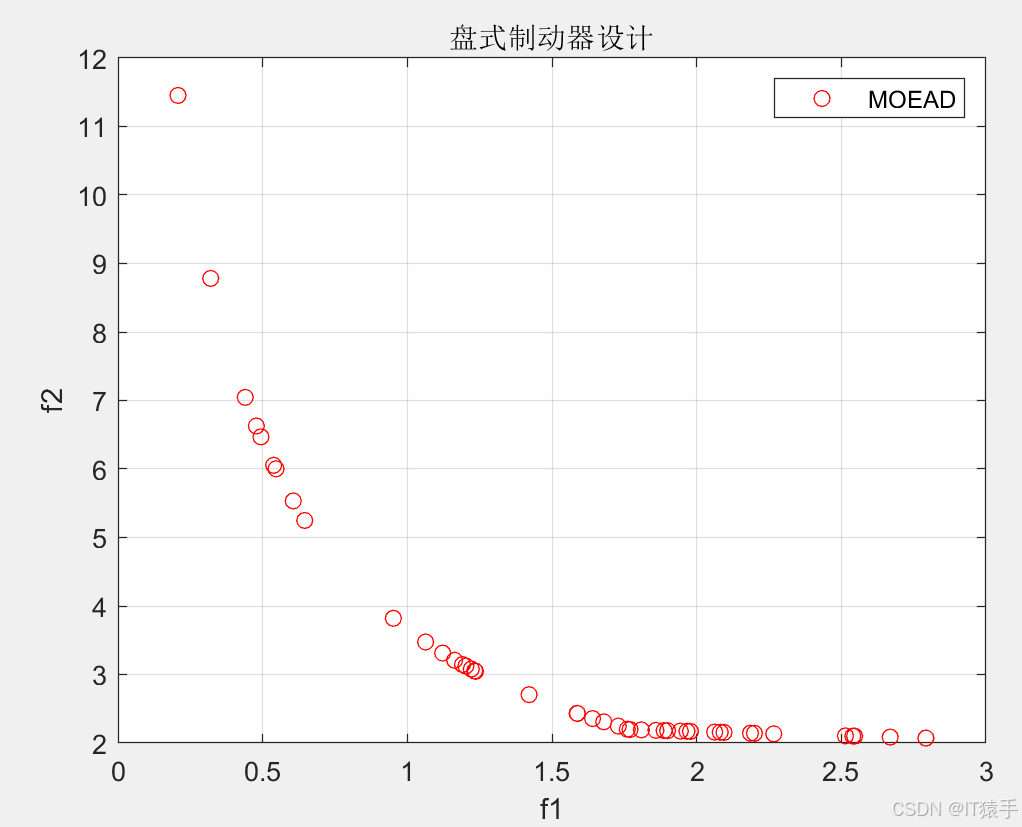
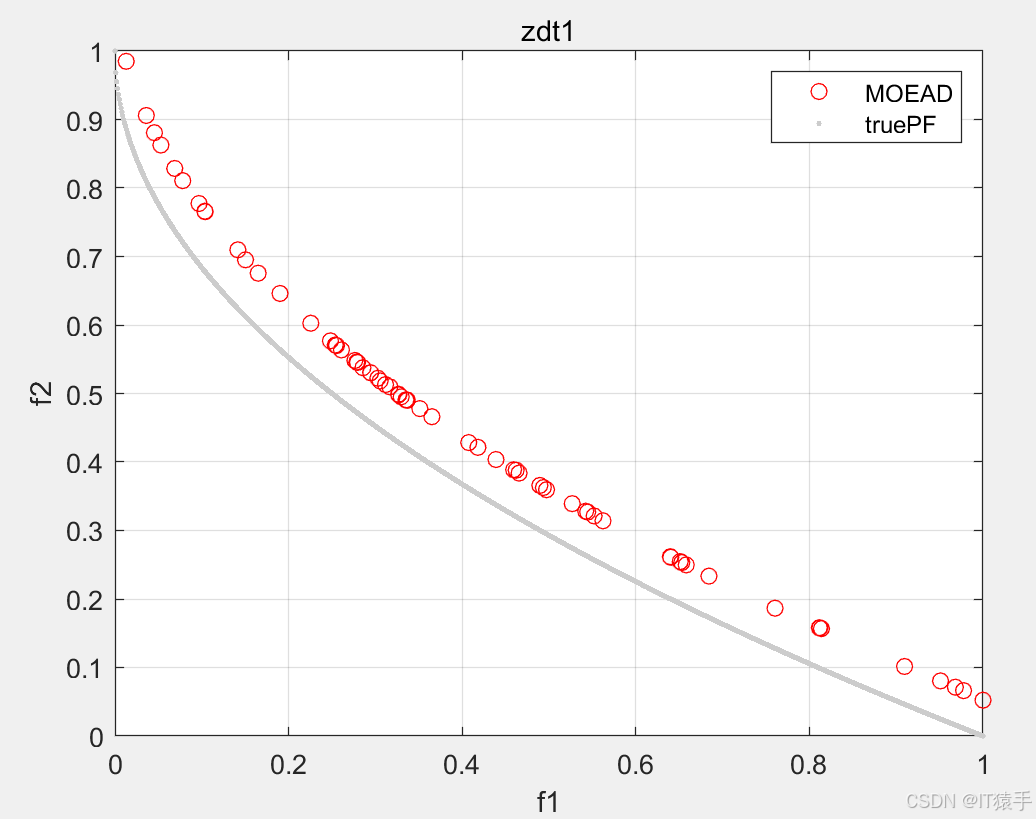
六、MOEA/D应用

MOEA/D用于求解46个多目标测试函数（ZDT1、ZDT2、ZDT3、ZDT4、ZDT6、DTLZ1-DTLZ7、WFG1-WFG10、UF1-UF10、CF1-CF10、Kursawe、Poloni、Viennet2、Viennet3）以及1个工程应用（盘式制动器设计）,并采用IGD、GD、HV、SP进行评价。

6.1部分代码

close all;
clear ; 
clc;
%%
% TestProblem测试问题说明：
%一共46个多目标测试函数，详情如下：
%1-5:ZDT1、ZDT2、ZDT3、ZDT4、ZDT6
%6-12：DZDT1-DZDT7
%13-22：wfg1-wfg10
%23-32：uf1-uf10
%33-42：cf1-cf10
%43-46:Kursawe、Poloni、Viennet2、Viennet3
%47 盘式制动器设计 温泽宇,谢珺,谢刚,续欣莹.基于新型拥挤度距离的多目标麻雀搜索算法[J].计算机工程与应用,2021,57(22):102-109.
%%
TestProblem=47;%1-47
MultiObj = GetFunInfo(TestProblem);
MultiObjFnc=MultiObj.name;%问题名
% Parameters
params.Np = 100;        % Population size
params.Nr = 100;        % Repository size
params.maxgen =100;    % Maximum number of generations
[x,f] = MOEAD(params,MultiObj);

6.2部分结果

八、完整MATLAB代码见下方名片