 🔥近津薪荼: [个人主页] 🎬个人专栏: 《近津薪荼的算法日迹》 《Linux操作系统及网络基础知识分享》 《c++基础知识详解》 《c语言基础知识详解》 ✨不要物化,矮化,弱化,钝化自己,保持锋芒,不要停止学习 这个世界上只有两个人真正在注意着你 八岁的你,和八十岁的你, 他们此刻正在注视着你, 一个希望你 勇敢开始 ,一个希望你 不留遗憾
🔥近津薪荼: [个人主页] 🎬个人专栏: 《近津薪荼的算法日迹》 《Linux操作系统及网络基础知识分享》 《c++基础知识详解》 《c语言基础知识详解》 ✨不要物化,矮化,弱化,钝化自己,保持锋芒,不要停止学习 这个世界上只有两个人真正在注意着你 八岁的你,和八十岁的你, 他们此刻正在注视着你, 一个希望你 勇敢开始 ,一个希望你 不留遗憾
1.上期参考代码
全局变量
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
vector<string> ret;
string path;
public:
vector<string> binaryTreePaths(TreeNode* root) {
if(root==nullptr) return ret;
dfs(root);
return ret;
}
void dfs(TreeNode* root) {
if(root==nullptr) return ;
// 记录当前节点值的长度,后边回溯会用
int val_len = to_string(root->val).size();
path += to_string(root->val);
if(root->left==nullptr && root->right==nullptr) {
ret.push_back(path);
} else {
// 非叶子节点,才拼接"->"
if(root->left) {
path += "->";
dfs(root->left);
// 回溯:删除拼接的"->"(2个字符)
path.pop_back();
path.pop_back();
}
if(root->right) {
path += "->";
dfs(root->right);
path.pop_back();
path.pop_back();
}
}
// 回溯:删除当前节点的值(按长度删)
for(int i = 0; i < val_len; i++) {
path.pop_back();
}
}
};传值传参
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
vector<string> ret;
public:
vector<string> binaryTreePaths(TreeNode* root) {
string path;
if(root==nullptr) return ret;
dfs(root,path);
return ret;
}
void dfs(TreeNode* root,string path)
{
if(root==nullptr)return ;
///////////////////////////////////////////////////////////////////出口
path += to_string(root->val);
if(root->left==nullptr&&root->right==nullptr)
{
ret.push_back(path);
}
path +="->";
dfs(root->left,path);
dfs(root->right,path);
/////////////////////////////////////////////////////////////////每一层子问题要做的事
}
};2.本期知识点导图
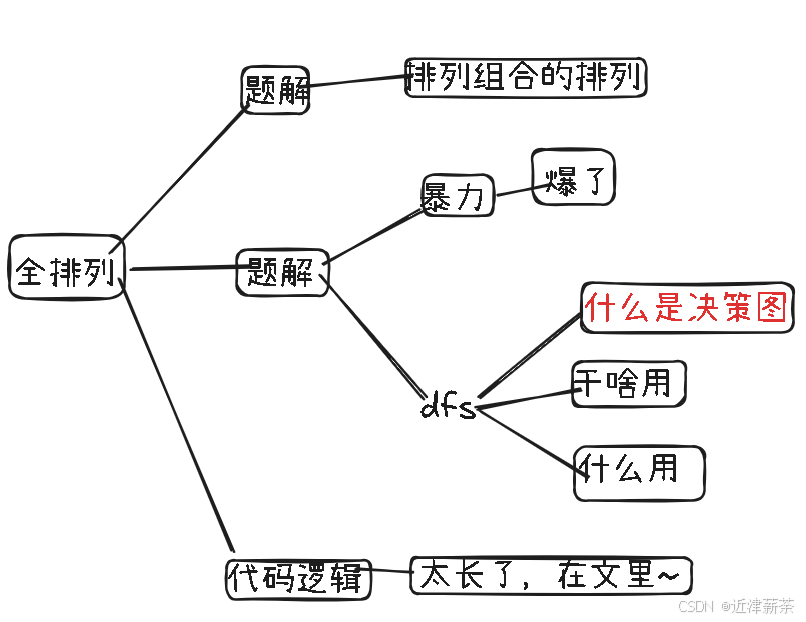
3.本期要讲解的题目是
全排列

要点:
- 就是高中学的排列
4.解题
4.1 暴力解法:枚举
嵌套循环,一 一枚举,有几个数就套几层循环,第一层循环做第一个数,以此类推,时间复杂度爆大
4.2优解
我们上过初高中吧,那肯定也画过树状图来解决简单的排列组合吧
我们来画一个:
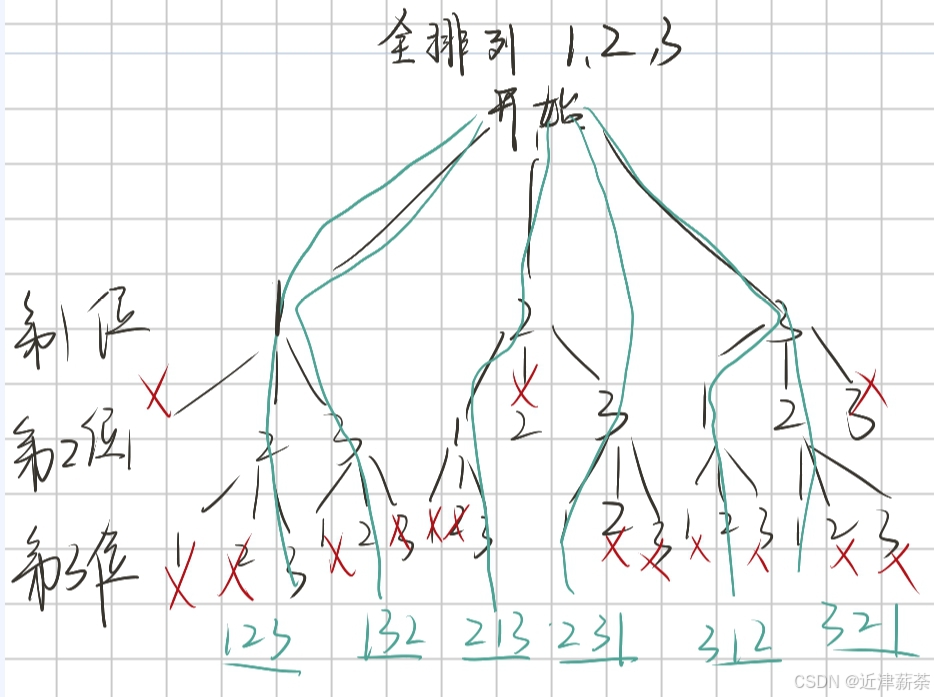
在我们的算法思想中,上边画的树状图是一个决策树
什么是决策树?
- 决策树就是像问问题一样层层分叉、根据特征一步步筛选,最终得到分类或预测结果的树形判断模型。
听上去高大上,说白了就是画树状图分析问题
我们后续学习难一点的dfs,都要开始画决策图啦
我们的回溯和剪枝思想离不开决策图 ,画图能帮助我们快速决策 在什么地方剪枝,回溯应该怎么操作
比如这题:
- 全排列,没有重复的元素(所以对使用过的元素,我们应该加上标记),我画红叉的地方就是该剪枝的地方。
- 回溯时的操作应该是将使用标记改成未使用,将放入数组的元素删去(结合代码逻辑理解)
为什么一定要有回溯操作?
以后做dfs的题,我们可以先画决策图,不是递归图,是决策图,看图写代码会顺畅很多。
代码逻辑
- 先画图:
通过分析我们发现需要做三个核心操作
- 用一维数组path记录元素形成排列
- 用二维数组ret记录排列,作为返回值
- 用一个bool类型的数组记录元素是否被使用过
-
重复子问题:求一组元素的排列(每次求得排列不得重复)
看看上边用到的数组,如果全部设置成函数参数,那会变得很麻烦。
那就意味着我们得使用全局变量,使用全局变量的话,回溯操作不可避免的~~
-
子问题干什么:
- 将未使用过的元素放入path(剪枝)
- 将元素标记成已使用
- 排列剩下的元素
- 回溯:将刚才的元素置为未使用,并移出path
- 出口:当path放满nums.size( )个元素时,将path放如ret,返回
提示:数组递归,经常使用for循环来建立框架
5.下期要讲解的题目是:
子集
6.嗟食
如果小编写的内容对佬有帮助,还请大佬点点三连加关注哦 
佬的支持就是我前进的最大动力  ~
~
期待与佬的再次相遇~