单链表算法题思路详解（上）

目录

一、移除链表元素

（一）题目描述

（二）解题思路（新建链表法）

（三）代码实现

二、反转链表

（一）题目描述

（二）解题思路（三指针原地修改法）

（三）代码实现

三、链表的中间结点

（一）题目描述

（二）解题思路（快慢指针法）

（三）代码实现

四、合并两个有序链表

（一）题目描述

Tip：归并排序里面，合并两个链表，并进行排序，就可以使用这个算法。

（二）解题思路

（三）代码实现

五、链表分割

（一）题目描述

（二）算法核心思想

（三）代码实现

（四）易错点与注意事项

（五）算法复杂度分析

六、链表的回文结构

（一）题目描述

（二）解题思路

（三）代码实现

---

一、移除链表元素

（一）题目描述

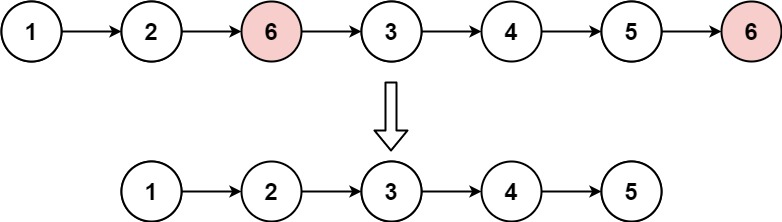
**1、题目简述：**给你一个链表的头结点 head 和一个整数 val，删除链表中所有值为 val 的结点，返回新的头节点。

2、题目链接： https://leetcode.cn/problems/remove-linked-list-elements/description/

（二）解题思路（新建链表法）

1、创建 "虚拟头尾指针"（newHead、newTail），初始为空，用于构建新链表（只包含值不为val的节点）。

2、遍历原链表，若当前节点值不为val，则将其尾插至新链表。

3、 尾插后需将新链表尾节点的next置空，避免指向原链表的冗余节点，导致输出错误。

这里并不是说我创建了一个全新的链表，而是说再原来链表结点的基础上，重构了连接逻辑。最后得到了这一个 "新" 的链表。

（三）代码实现

// 注：LeetCode中节点结构体名为ListNode，需适配
typedef struct ListNode ListNode;
struct ListNode* removeElements(struct ListNode* head, int val) 
{
    // 1. 定义虚拟头尾指针（初始为空）
    ListNode* newHead = NULL;
    ListNode* newTail = NULL;
    ListNode* pcur = head;  // 遍历原链表的临时指针

    // 2. 遍历原链表，筛选值不为val的结点
    while (pcur) {
        if (pcur->val != val) {
            if (newHead == NULL) {
                // 新链表为空，当前节点作为首结点
                newHead = newTail = pcur;
            } else {
                // 新链表非空，尾插至末尾并更新尾指针
                newTail->next = pcur; //插入结点
                newTail = newTail->next; //更新尾结点
            }
        }
        pcur = pcur->next;  // 移动到下一个结点
    }

    // 3. 确保新链表尾结点next置空（避免野指针）
    if (newTail) {
        newTail->next = NULL;
    }

    return newHead;  // 返回新链表头结点
}

二、反转链表

（一）题目描述

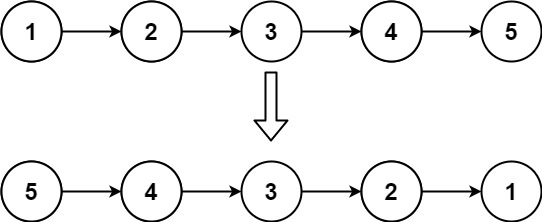
**1、题目简述：**给你单链表的头节点head，请你反转链表，并返回反转后的链表的头节点（如输入1→2→3→4→5，输出5→4→3→2→1。

2、题目链接： https://leetcode.cn/problems/reverse-linked-list/description/

（二）解题思路（三指针原地修改法）

1、定义三个指针

**（1）n1：**前驱指针，初始为NULL（反转后第一个结点的next为NULL）。

**（2）n2：**当前结点指针，初始为head（从首结点开始修改）。

**（3）n3：**后继指针，初始为head->next（保存n2的下一个结点，避免修改后丢失）。

**2、**循环修改 n2 的 next 指向 n1，依次移动三个指针，直至 n2 为空（遍历结束）。

**3、**最终 n1 即为反转后的头节点（ n2 为空时，n1 指向原尾节点）。

就是说我们从头开始，依次向后断开链接，然后再向前链接。**即断开后面的牵手，然后向前面牵手。**以下为具体的演示图：

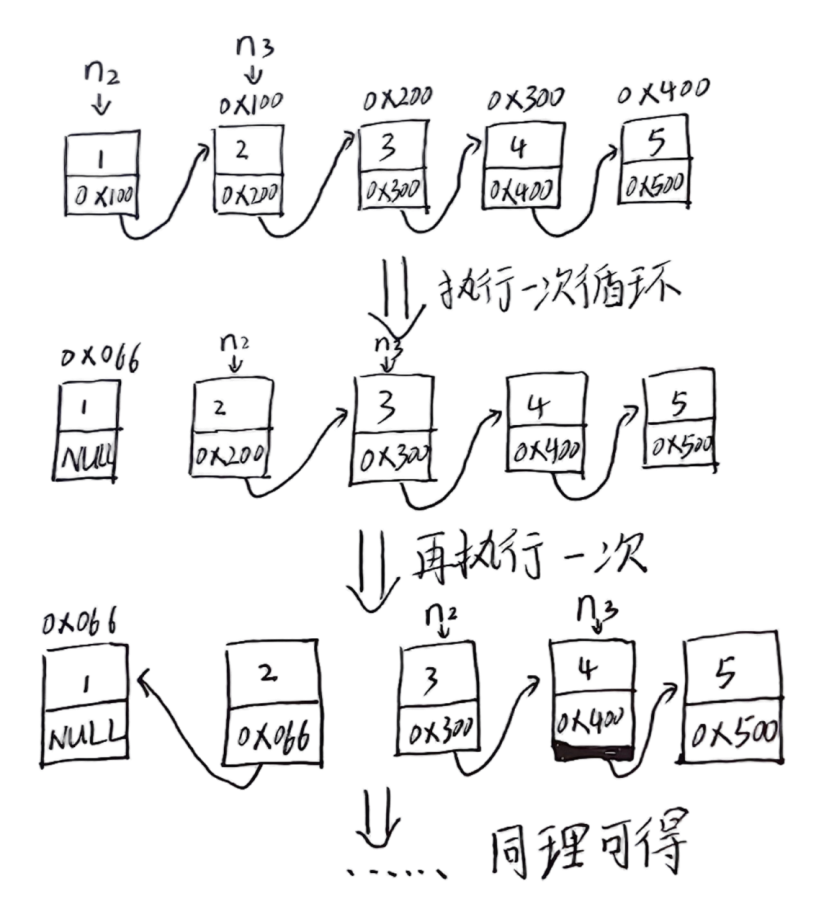
（三）代码实现

typedef struct ListNode ListNode;
struct ListNode* reverseList(struct ListNode* head) 
{
    // 空链表直接返回
    if (head == NULL) {
        return head;
    }

    ListNode* n1 = NULL;
    ListNode* n2 = head;
    ListNode* n3 = n2->next;

    while (n2) {
        // 1. 反转当前节点的指针指向
        n2->next = n1;

        // 2. 移动三个指针
        n1 = n2;
        n2 = n3;

        // 3. 避免n3为空时解引用（最后一次循环n3为NULL）
        if (n3) {
            n3 = n3->next;
        }
    }

    return n1;  // n1为反转后的头节点
}

三、链表的中间结点

（一）题目描述

**1、题目简述：**给定一个头节点为 head 的非空单链表，返回链表的中间节点。如果有两个中间节点，则返回第二个中间节点（如输入1→2→3→4→5，输出3；输入1→2→3→4，输出3）。

**2、题目链接：**https://leetcode.cn/problems/middle-of-the-linked-list/description/

（二）解题思路（快慢指针法）

1、定义 "快慢指针"

**（1）slow（慢指针）：**每次移动 1 步。

**（2）fast（快指针）：**每次移动 2 步。

**2、循环条件：**fast && fast->next（确保快指针不会空指针解引用，比如NULL->next）。

**3、逻辑推导：**当快指针到达链表末尾时，慢指针恰好走了快指针路程的一半，即指向中间结点（偶数节点时指向第二个中间结点）。

（三）代码实现

typedef struct ListNode ListNode;
struct ListNode* middleNode(struct ListNode* head) 
{
    ListNode* slow = head;
    ListNode* fast = head;

    // 循环条件：fast非空且fast的下一个节点非空（避免快指针越界）
    while (fast && fast->next) {
        slow = slow->next;          // 慢指针走1步
        fast = fast->next->next;    // 快指针走2步
    }

    return slow;  // slow指向中间节点
}

**四、**合并两个有序链表

（一）题目描述

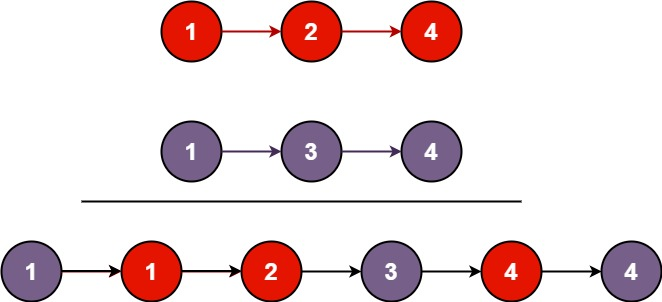
**1、题目简述：**将两个升序单链表list1和list2合并为一个新的升序单链表，新链表由原两个链表的所有结点组成，返回新链表头结点。

**2、题目链接：**https://leetcode.cn/problems/merge-two-sorted-lists/description/

**Tip：**归并排序里面，合并两个链表，并进行排序，就可以使用这个算法。

（二）解题思路

解题思路一：基础尾插法

1、核心逻辑：创建空链表，双指针遍历两个原链表，比较结点值，将较小值结点尾插至新链表，剩余结点直接链接。

2、步骤拆解

**（1）边界处理：**若 list1 为空，返回 list2；若 list2 为空，返回list1（覆盖两者均为空的情况）。

（2）初始化

①新链表头尾指针newHead = NULL，newTail = NULL。

②定义遍历指针 l1 = list1，l2 = list2。

**（3）**循环遍历（ l1 和 l2 均非空）

若 l1->val < l2->val：将 l1 尾插至新链表，l1 = l1->next；否则：将l2尾插至新链表，l2 = l2->next。

尾插逻辑：新链表为空时，newHead = newTail = 当前结点；新链表非空时，newTail->next = 当前节点，newTail = newTail->next，即让新结点变成newtail。

**（4）处理剩余结点：**若l1非空：newTail->next = l1；若l2非空：newTail->next = l2。

**（5）返回结果：**返回newHead。

3、复杂度分析

**（1）时间复杂度：**O (n+m)（n、m为两链表长度，仅一次遍历）。

**（2）空间复杂度：**O (1)。

4、缺陷：空链表判断导致代码冗余（尾插时需反复判断newHead是否为空）。

解题思路二：哨兵节点优化法（最优）

1、核心逻辑：创建一个 "哨兵节点"（不存储有效数据，仅占位），使新链表初始非空，消除空链表判断，简化代码。

2、步骤拆解

**（1）边界处理：**同思路 1（list1或list2为空时直接返回）。

（2）初始化

**① 申请哨兵节点：**newHead = (ListNode*)malloc(sizeof(ListNode))，newTail = newHead。即新链表初始非空。

② 定义遍历指针 l1 = list1，l2 = list2。

③ 循环遍历（l1和l2均非空）：

比较结点值，将较小结点尾插至 newTail 后；

尾插逻辑： newTail->next = 较小结点，newTail = newTail->next，对应遍历指针后移。

**（3）处理剩余结点：**newTail->next = l1 != NULL ? l1 : l2。

（4）释放哨兵结点

保存实际头结点：ListNode* ret = newHead->next；释放哨兵结点内存：free(newHead)，newHead = NULL，newTail = NULL。

**（5）返回结果：**返回 ret。

**3、核心优势：**消除所有空链表判断，代码简洁（尾插时无需判断newHead是否为空）。内存可回收，避免内存泄漏。

（三）代码实现

typedef struct ListNode ListNode;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) 
{
    // 边界处理：任一链表为空，返回另一链表
    if (list1 == NULL) 
        return list2;
    if (list2 == NULL) 
        return list1;
    
    // 创建哨兵结点，新链表初始非空
    ListNode* newHead = (ListNode*)malloc(sizeof(ListNode));
    ListNode* newTail = newHead;
    ListNode* l1 = list1;
    ListNode* l2 = list2;
    
    // 遍历两链表，尾插较小结点
    while (l1 != NULL && l2 != NULL) {
        if (l1->val < l2->val) {
            newTail->next = l1;
            l1 = l1->next;
        } else {
            newTail->next = l2;
            l2 = l2->next;
        }
        newTail = newTail->next;
    }
    
    // 链接剩余结点
    if (l1 != NULL) {
        newTail->next = l1;
    } else {
        newTail->next = l2;
    }
    
    // 释放哨兵结点，返回实际头结点
    ListNode* ret = newHead->next;
    free(newHead);
    newHead = NULL;
    newTail = NULL;
    
    return ret;
}

五、链表分割

（一）题目描述

1、题目简述

现有一链表的头指针 ListNode* pHead，给一定值x，编写一段代码将所有小于x的结点排在其余结点之前，且不能改变原来的数据顺序，即数据具有稳定性，返回重新排列后的链表的头指针。

**2、题目链接：**https://www.nowcoder.com/practice/0e27e0b064de4eacac178676ef9c9d70

3、数据结构定义（C++）

struct ListNode {
    int val;
    ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};

（二）算法核心思想

1、核心思路

通过 **"拆分 - 合并"**实现，避免在原链表上直接修改（减少复杂度）：

（1）创建两个带头空链表（哨兵结点），分别存储两类结点。

**（2）**遍历原链表，按结点值与 x 的大小关系，尾插至对应链表。

**（3）**合并两个链表，处理边界避免循环引用。

**（4）**释放临时哨兵结点，返回有效头指针。

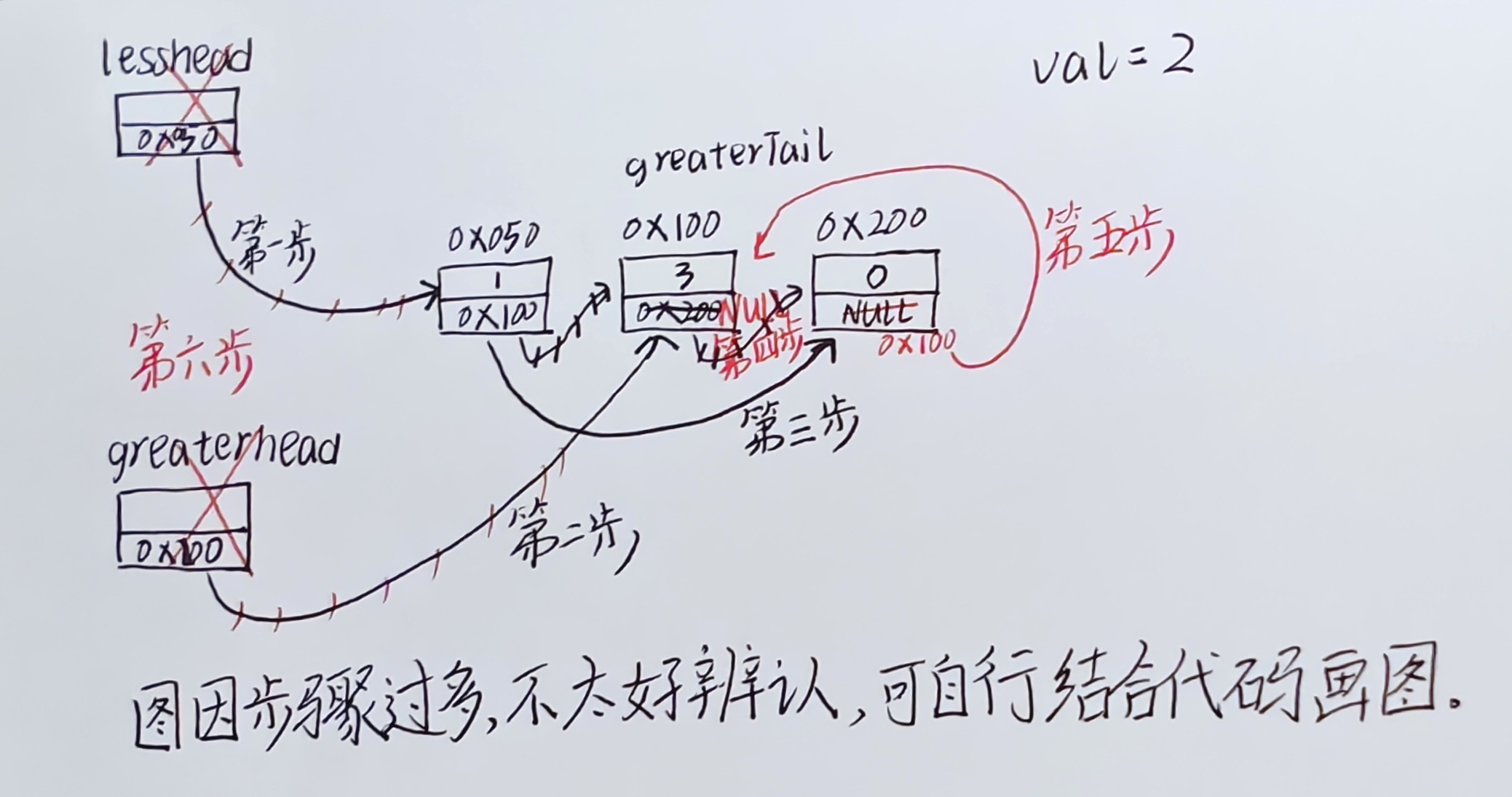
2、关键设计

**（1）**小链表（lessHead / lessTail）：存储所有小于 x 的结点。

**（2）**大链表（greaterHead / greaterTail）：存储所有大于或等于 x 的结点。

**（3）哨兵节点作用：**无需判断链表是否为空，简化尾插操作。

**其实本质上就是：**有两个头结点，然后不断地去连接链表上的结点，改变它们的连接顺序。最后遇到原链表两个结点分不开，将大链表的指针域置为nullptr（C++中空指针的表示），再将小链表与大链表连接，实现了完美的断开，同时处理了大链表的头结点。

（三）代码实现

class Partition {
public:
    ListNode* partition(ListNode* pHead, int x) 
    {
        // 1. 初始化两个带头空链表
        ListNode* lessHead = (ListNode*)malloc(sizeof(ListNode));
        ListNode* lessTail = lessHead;
        ListNode* greaterHead = (ListNode*)malloc(sizeof(ListNode));
        ListNode* greaterTail = greaterHead;
        
        // 2. 遍历原链表分类尾插
        ListNode* pcur = pHead;
        while (pcur) {
            if (pcur->val < x) {
                lessTail->next = pcur;
                lessTail = lessTail->next;
            } else {
                greaterTail->next = pcur;
                greaterTail = greaterTail->next;
            }
            pcur = pcur->next;
        }
        
        // 3. 处理边界并合并
        // 这样完美处理了原链表有两个结点没有分开的问题
        // 同时也完美处理了大链表的空头结点
        greaterTail->next = nullptr;
        lessTail->next = greaterHead->next;
        
        // 4. 释放内存并返回
        ListNode* ret = lessHead->next;
        free(lessHead);
        free(greaterHead);
        return ret;
    }
};

（四）易错点与注意事项

1、必须处理大链表尾节点

未置空 greaterTail->next 会导致链表成环（如原链表 6→2，合并后 6 仍指向 2，遍历无限循环）；一旦后续进行遍历操作，就会造成内存超限、程序卡死。

2、内存泄漏问题

动态申请的哨兵结点（lessHead/greaterHead）使用后必须释放；释放前需先保存结果头指针（ret = lessHead->next），否则会丢失链表起始位置。

3、保持相对顺序

采用 "尾插" 方式确保结点原始顺序不变，若使用头插会反转顺序，违反题目要求。

4、空链表处理

若原链表为空（pHead = nullptr），最终返回lessHead->next（仍为nullptr），逻辑自洽无需额外判断。

（五）算法复杂度分析

**1、时间复杂度：**O (n)，仅遍历原链表一次，每个结点操作均为 O (1)。

**2、空间复杂度：**O (1)，仅额外申请两个哨兵结点，不随输入规模变化。

六、链表的回文结构

（一）题目描述

1、题目简述

给定单链表的头结点 A，设计时间复杂度 O (n)、空间复杂度 O (1) 的算法，判断链表是否为回文结构（链表长度≤900）。

回文结构定义：以中心点为对称轴，左右两部分节点值完全对称（示例：1->2->2->1为回文，1->2->3->1非回文）。

**2、题目链接：**https://www.nowcoder.com/practice/d281619e4b3e4a60a2cc66ea32855bfa

（二）解题思路

解题思路 1：链表转数组法（投机取巧）

**1、核心逻辑：**利用题目 "链表长度≤900" 的限制，创建固定大小数组存储结点值，再用双指针判断数组是否为回文。

2、步骤拆解

**（1）初始化数组：**int arr[900] = {0}，计数器i = 0。

**（2）遍历链表：**pcur = A，将pcur->val依次存入arr[i]，i++，pcur = pcur->next。

（3）双指针判断回文

left = 0（数组起始），right = i - 1（数组末尾，有效数据最后一位）；循环条件：left < right。若 arr[left] != arr[right]，返回 false；否则 left++，right--。

**（4）****返回结果：**循环结束返回true。

3、复杂度分析

**（1）时间复杂度：**O (n)（一次遍历链表，一次遍历数组）。

**（2）空间复杂度：**O (1)（数组大小固定为 900，视为常数空间）。

**4、缺陷：**不通用，若题目无长度限制则失效。

思路 2：快慢指针 + 反转法（通用最优）

**1、核心逻辑：**分三步实现 → ①找中间节点；②反转后半链表；③比较前后两部分节点值。

2、步骤拆解

（1）步骤 1：找中间节点（复用 "链表的中间结点" 逻辑）

用快慢指针法，偶数节点最终取到靠右结点（如1->2->3->4取3），奇数结点最终取到正中结点（如1->2->3->4->5取3）。

（2）步骤 2：反转后半链表（复用 "反转链表" 逻辑）

以中间结点为头，调用反转函数，得到反转后的后半链表头结点rightHead。

（3）步骤 3：比较前后两部分

①初始化指针：left = A（原链表头），right = rightHead（反转后后半链表头）。

②循环条件：right != NULL（后半链表长度≤前半链表，先遍历完）。

③若 left->val != right->val，返回 false；否则 left = left->next，right = right->next。

**（4）返回结果：**循环结束返回 true。

3、关键原理：反转后半链表后，后半链表的遍历顺序与前半链表 "对称"，可通过同步遍历比较值是否一致。

（三）代码实现

typedef struct ListNode ListNode;

// 子函数1：找中间结点
ListNode* findMiddle(ListNode* head) 
{
    ListNode* slow = head;
    ListNode* fast = head;
    while (fast != NULL && fast->next != NULL) {
        slow = slow->next;
        fast = fast->next->next;
    }
    return slow;
}

// 子函数2：反转链表
ListNode* reverseList(ListNode* head) {
    if (head == NULL) {
        return head;
    }
    ListNode* n1 = NULL;
    ListNode* n2 = head;
    ListNode* n3 = head->next;
    while (n2 != NULL) {
        n2->next = n1;
        n1 = n2;
        n2 = n3;
        if (n3 != NULL) 
            n3 = n3->next;
    }
    return n1;
}

// 主函数：判断回文结构
bool chkPalindrome(ListNode* A) {
    // 步骤1：找中间结点
    ListNode* mid = findMiddle(A);
    
    // 步骤2：反转后半链表
    ListNode* rightHead = reverseList(mid);
    
     步骤3：比较前后两部分
    ListNode* left = A;
    ListNode* right = rightHead;
    while (right != NULL) {
        if (left->val != right->val) {
            return false;
        }
        left = left->next;
        right = right->next;
    }
    return true;
}