【强化学习教程——01_强化学习基石】第01章_MDP马尔可夫决策过程

第 1 章：MDP 马尔可夫决策过程

本章目标：理解强化学习的基本框架，掌握 MDP 五元组的数学定义，区分回报与奖励，并学会使用 OpenAI Gym 风格接口定义环境。

📖 目录 (Table of Contents)

什么是强化学习？
[MDP 五元组详解](#MDP 五元组详解)
案例研究：回收机器人
[价值体系：回报 vs 奖励](#价值体系：回报 vs 奖励)
马尔可夫性质
策略 (Policy)
[实战：定义 Gym 风格 MDP](#实战：定义 Gym 风格 MDP)
总结与预告

1. 什么是强化学习？

强化学习 (Reinforcement Learning) 是机器学习的第三范式，关注智能体 (Agent) 如何在环境 (Environment) 中通过试错 (Trial-and-Error) 来最大化累积奖励。

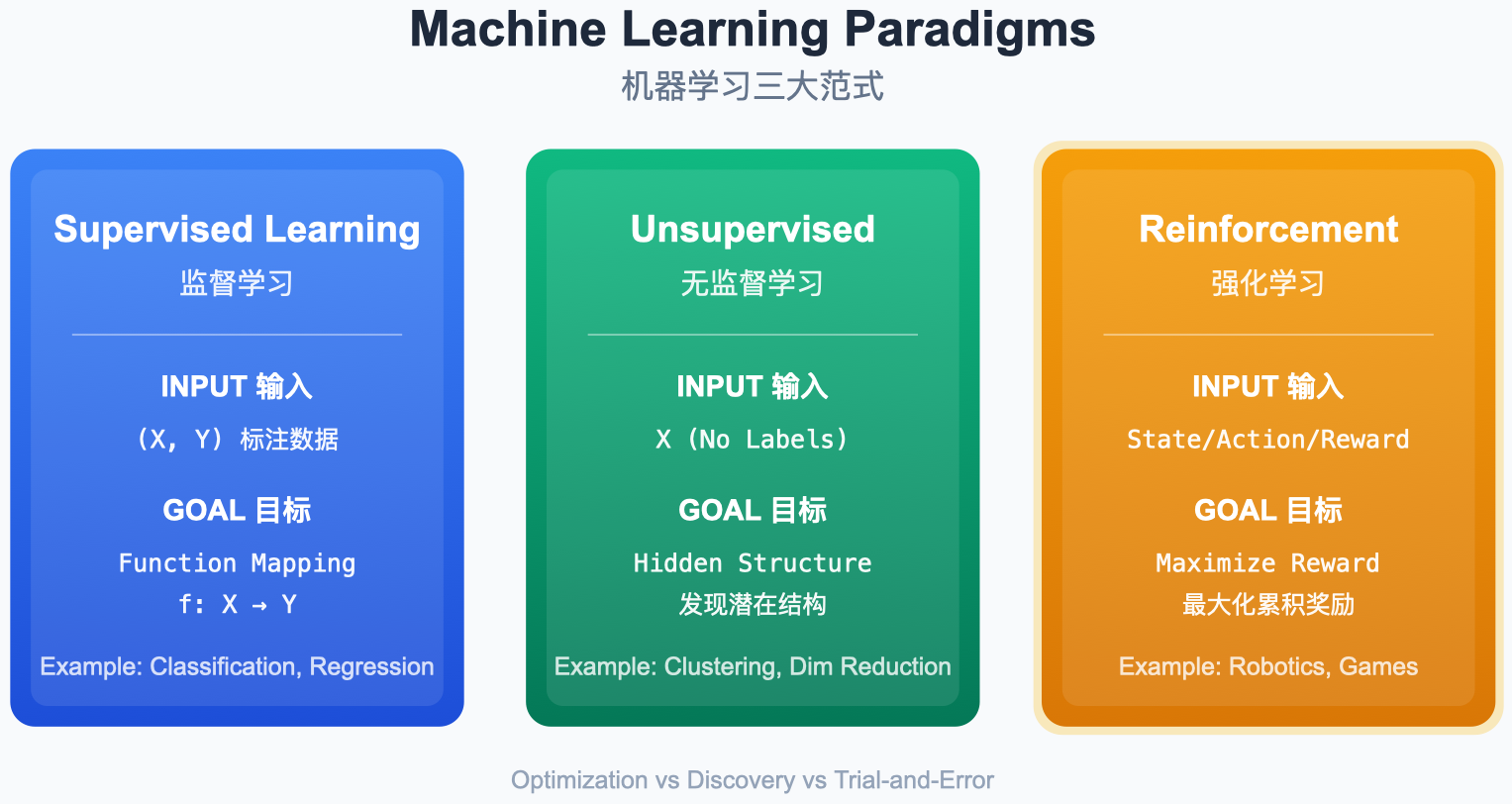
图解说明：

Supervised Learning：有标签数据，学习输入到输出的映射。

Unsupervised Learning：无标签数据，寻找数据内部结构。

Reinforcement Learning：通过与环境交互获得的奖励信号进行学习。

核心循环

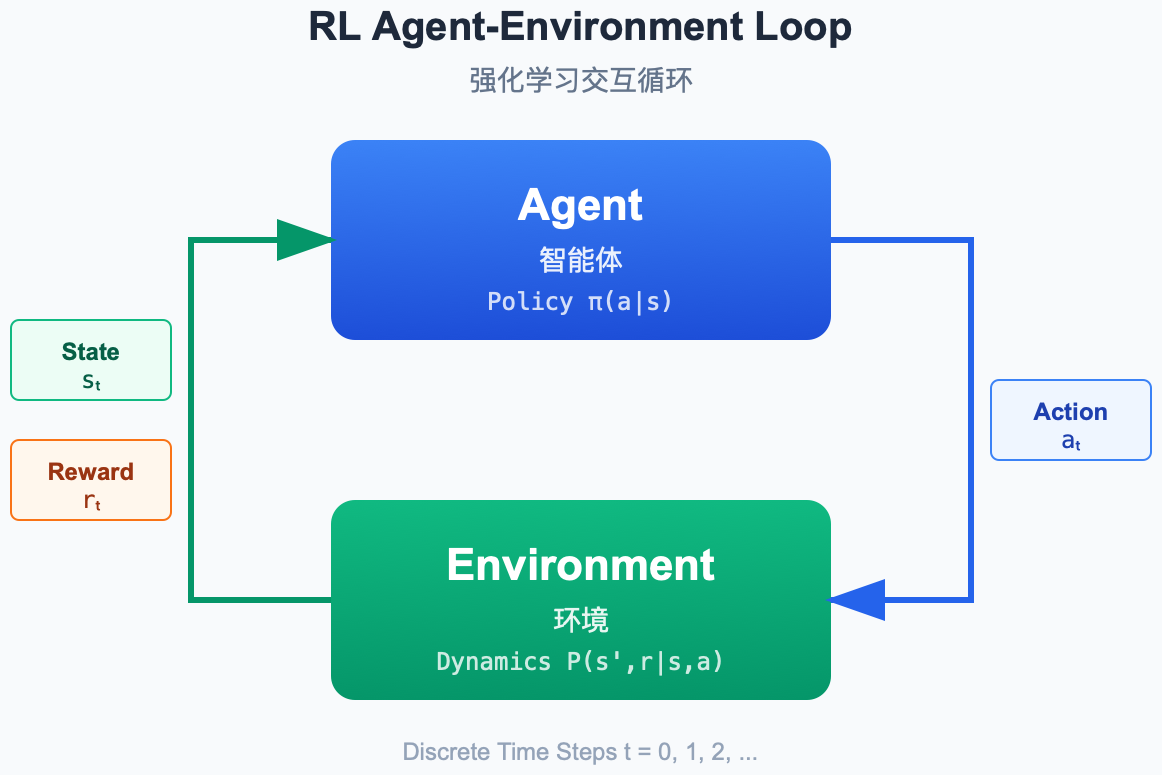
图解说明：

Agent (大脑) ：感知状态 S t S_t St，决策动作 A t A_t At。

Environment (世界) ：接收动作，反馈新状态 S t + 1 S_{t+1} St+1 和奖励 R t + 1 R_{t+1} Rt+1。

交互通道：状态、奖励（出），动作（入）。

2. MDP 五元组详解

马尔可夫决策过程 (Markov Decision Process) 是强化学习的数学基础，由五元组 ⟨ S , A , P , R , γ ⟩ \langle \mathcal{S}, \mathcal{A}, P, R, \gamma \rangle ⟨S,A,P,R,γ⟩ 正式定义：

符号	名称	英文	说明
S \mathcal{S} S	状态空间	State Space	所有可能状态的集合（有限或无限）
A \mathcal{A} A	动作空间	Action Space	智能体可执行的所有动作集合
P P P	动态模型	Transition Prob.	$P(s'
R R R	奖励函数	Reward Function	$R(s,a) = \mathbb{E}[R_{t+1}
γ \gamma γ	衰减系数	Discount Factor	γ ∈ [ 0 , 1 ] \gamma \in [0,1] γ∈[0,1]，权衡即时奖励与长期回报

状态转移矩阵

对于有限状态 MDP，动态模型 P P P 可表示为矩阵。对于每个动作 a a a，矩阵 P a \mathcal{P}^a Pa 为：

P a = [ P ( s 1 ∣ s 1 , a ) ... P ( s n ∣ s 1 , a ) ⋮ ⋱ ⋮ P ( s 1 ∣ s n , a ) ... P ( s n ∣ s n , a ) ] \mathcal{P}^a = \begin{bmatrix} P(s_1|s_1, a) & \dots & P(s_n|s_1, a) \\ \vdots & \ddots & \vdots \\ P(s_1|s_n, a) & \dots & P(s_n|s_n, a) \end{bmatrix} Pa= P(s1∣s1,a)⋮P(s1∣sn,a)...⋱...P(sn∣s1,a)⋮P(sn∣sn,a)

每一行的概率之和必须为 1。

3. 案例研究：回收机器人

引用 Sutton 书中的经典案例：一个负责收集空罐子的移动机器人。

3.1 定义五元组

状态空间 S \mathcal{S} S : 电量状态 { High , Low } \{\text{High}, \text{Low}\} {High,Low}
动作空间 A \mathcal{A} A :
- High \text{High} High: { Search , Wait } \{\text{Search}, \text{Wait}\} {Search,Wait}
- Low \text{Low} Low: { Search , Wait , Recharge } \{\text{Search}, \text{Wait}, \text{Recharge}\} {Search,Wait,Recharge}
参数 : α \alpha α (保持 High 概率), β \beta β (不耗尽概率), r s e a r c h r_{search} rsearch, r w a i t r_{wait} rwait。

3.2 状态转移图 (Transition Graph)

Wait, r_w
Search, r_s, 1-α
Wait, r_w
Search, -3, 1-β
Recharge, 0
High
Low

图解说明：

节点：代表状态 (High/Low)。

边：代表动作及转移概率。

标签：格式为 Action, Reward, Probability。

3.3 数学形式化

设 α = 0.7 , β = 0.5 , r s e a r c h = 5 , r w a i t = 1 \alpha=0.7, \beta=0.5, r_{search}=5, r_{wait}=1 α=0.7,β=0.5,rsearch=5,rwait=1：

P ( s ′ ∣ s = High , a = Search ) = { 0.7 s ′ = High 0.3 s ′ = Low P(s' | s=\text{High}, a=\text{Search}) = \begin{cases} 0.7 & s'=\text{High} \\ 0.3 & s'=\text{Low} \end{cases} P(s′∣s=High,a=Search)={0.70.3s′=Highs′=Low

R ( s = Low , a = Search ) = β ⋅ r s e a r c h + ( 1 − β ) ⋅ ( − 3 ) = 1.0 R(s=\text{Low}, a=\text{Search}) = \beta \cdot r_{search} + (1-\beta) \cdot (-3) = 1.0 R(s=Low,a=Search)=β⋅rsearch+(1−β)⋅(−3)=1.0

4. 价值体系：回报 vs 奖励

初学者容易混淆 R t R_t Rt 和 G t G_t Gt：

奖励 ( R t R_t Rt) : 即时反馈 。环境在 t t t 时刻给出的标量信号。
回报 ( G t G_t Gt) : 长期目标 。从 t t t 时刻开始，未来所有奖励的折现总和。

G t ≐ R t + 1 + γ R t + 2 + γ 2 R t + 3 + ... = ∑ k = 0 ∞ γ k R t + k + 1 G_t \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \ldots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} Gt≐Rt+1+γRt+2+γ2Rt+3+...=k=0∑∞γkRt+k+1

递归形式 ：
G t = R t + 1 + γ G t + 1 G_t = R_{t+1} + \gamma G_{t+1} Gt=Rt+1+γGt+1

折扣因子 γ \gamma γ 的作用：

数学收敛性：防止无限回报。
不确定性：未来不如当前可靠。
金融逻辑：即时满足优于延迟满足。

5. 马尔可夫性质

核心定义 ：未来的状态 S t + 1 S_{t+1} St+1 仅取决于当前状态 S t S_t St 和当前动作 A t A_t At，与历史无关。

P ( S t + 1 ∣ S t , A t ) = P ( S t + 1 ∣ S t , A t , S t − 1 , A t − 1 , ... ) P(S_{t+1} | S_t, A_t) = P(S_{t+1} | S_t, A_t, S_{t-1}, A_{t-1}, \dots) P(St+1∣St,At)=P(St+1∣St,At,St−1,At−1,...)

什么时候假设失效？

部分可观测 (POMDP): 如扑克牌，只看当前手牌不够，需记忆出牌历史。
非平稳环境: 环境规则随时间改变（如机械磨损）。
状态定义不完整: 如自动驾驶单张图片无法判断速度。

6. 策略 (Policy)

策略 π \pi π 是从状态到动作的映射，是 RL 的学习目标。

确定性策略 : a = π ( s ) a = \pi(s) a=π(s)
随机策略 : π ( a ∣ s ) = P ( A t = a ∣ S t = s ) \pi(a|s) = P(A_t=a | S_t=s) π(a∣s)=P(At=a∣St=s)

代码实现 (策略类型)

python 复制代码

import numpy as np

# 1. 确定性策略示例
def deterministic_policy(state, Q_table):
    # 直接选择价值最大的动作
    return np.argmax(Q_table[state])

# 2. 随机策略示例 (Softmax)
def softmax_policy(state, Q_table, temperature=1.0):
    preferences = Q_table[state] / temperature
    exp_p = np.exp(preferences - np.max(preferences)) # 防止溢出
    probs = exp_p / np.sum(exp_p)
    return np.random.choice(len(probs), p=probs)

7. 实战：定义 Gym 风格 MDP

OpenAI Gym (现 Gymnasium) 定义了标准接口。

代码实现 (SimpleWalkEnv)

python 复制代码

from abc import ABC, abstractmethod
from typing import Tuple, Dict, Any

class Environment(ABC):
    """标准的 RL 环境接口"""
    @abstractmethod
    def reset(self) -> Tuple[Any, Dict]: pass
    @abstractmethod
    def step(self, action: Any) -> Tuple[Any, float, bool, bool, Dict]: pass

# 极简 MDP：一维行走
class SimpleWalkEnv(Environment):
    def __init__(self):
        self.state = 0
        self.target = 3

    def reset(self):
        self.state = 0
        return self.state, {}

    def step(self, action):
        # Action: 0=Left, 1=Right
        move = -1 if action == 0 else 1
        self.state += move

        # 限制范围 [-1, 4]
        self.state = max(-1, min(4, self.state))

        # 奖励设定
        if self.state == self.target:
            return self.state, 1.0, True, False, {}
        else:
            return self.state, -0.1, False, False, {} # 每步微小惩罚

8. 总结与预告

本章核心：

MDP 是 RL 的数学建模，包含 S , A , P , R , γ S, A, P, R, \gamma S,A,P,R,γ。
马尔可夫性质 意味着"历史无关性"，是简化的关键。
Return ( G t G_t Gt) 是目标，Reward ( R t R_t Rt) 是手段。
策略 ( π \pi π) 是解，告诉我们在每个状态下该做什么。

下一章预告 ：

我们将深入探讨如何通过贝尔曼方程 (Bellman Equation) 来评估一个策略的好坏，并以此寻找最优策略。

➡️ 下一章：第 2 章：贝尔曼方程与价值函数