【强化学习教程——01_强化学习基石】第05章_时序差分学习

第 5 章：时序差分学习

本章目标 ：理解时序差分 (TD) 学习如何结合蒙特卡洛 (MC) 和动态规划 (DP) 的优点，掌握 TD(0) 算法、n-step TD 以及 TD( λ \lambda λ) 与资格迹的概念，深入理解偏差-方差权衡。

📖 目录 (Table of Contents)

[TD 的核心思想](#TD 的核心思想)
[TD vs MC 对比](#TD vs MC 对比)
[TD(0) 预测](#TD(0) 预测)
[n-step TD](#n-step TD)
[TD(λ) 与资格迹](#TD(λ) 与资格迹)
回溯更新图解 (Backup Diagram)
偏差-方差权衡
[TD 学习的收敛性](#TD 学习的收敛性)
总结与预告

1. TD 的核心思想

时序差分 (Temporal-Difference, TD) 学习是强化学习中最核心的思想之一。它的创新在于：不需要等到一个 Episode 结束，每走一步就可以更新价值估计。

TD 融合了两种方法的优点：

从 蒙特卡洛 (MC) 继承了从真实经验中采样的能力，不需要环境模型。
从 动态规划 (DP) 继承了自举 (Bootstrapping) 的思想，用当前的估计值来更新估计值。

直觉理解：考试后不用等公布成绩（MC），也不用知道标准答案（DP），做完每道题立马根据感觉调整策略。

2. TD vs MC 对比

特性	蒙特卡洛 (MC)	时序差分 (TD)
更新时机	Episode 结束后	每一步 (Step-by-step)
自举 (Bootstrapping)	否 (使用真实回报 G t G_t Gt)	是 (使用估计值 V ( S t + 1 ) V(S_{t+1}) V(St+1))
方差	高 (受整条轨迹随机性影响)	低 (仅受一步随机性影响)
偏差	无 (无偏估计)	有 (初始估计偏差，渐近无偏)
是否需要完整 Episode	是	否
适用场景	仅限 Episodic 任务	Episodic 或 Continuing 任务
对初值敏感	否	是

经典案例：Driving Home（回家路上的预估）

假设你从公司开车回家，经过若干地点，每个地点都有一个"到家时间"的预估：

地点	已用时间	当时预估总时间
出发（公司）	0 min	30 min
上高速	5 min	35 min
高速出口	20 min	35 min
小区门口	30 min	40 min
到家	43 min	43 min

MC 更新 ：到家后（43分钟），回头把所有地点的预估都更新为 43 分钟。信息利用效率低，但无偏。
TD 更新 ：离开公司（预估30）到了堵车点（预估35，已过5分钟），新预估 = 5 + 35 = 40。发现比原来多了 10 分钟，立刻更新公司处的预估： V ( 公司 ) ← 30 + α ( 40 − 30 ) V(\text{公司}) \leftarrow 30 + \alpha(40 - 30) V(公司)←30+α(40−30)。不需要等到家。

3. TD(0) 预测

TD(0) 是最基本的 TD 算法，只向前看一步。

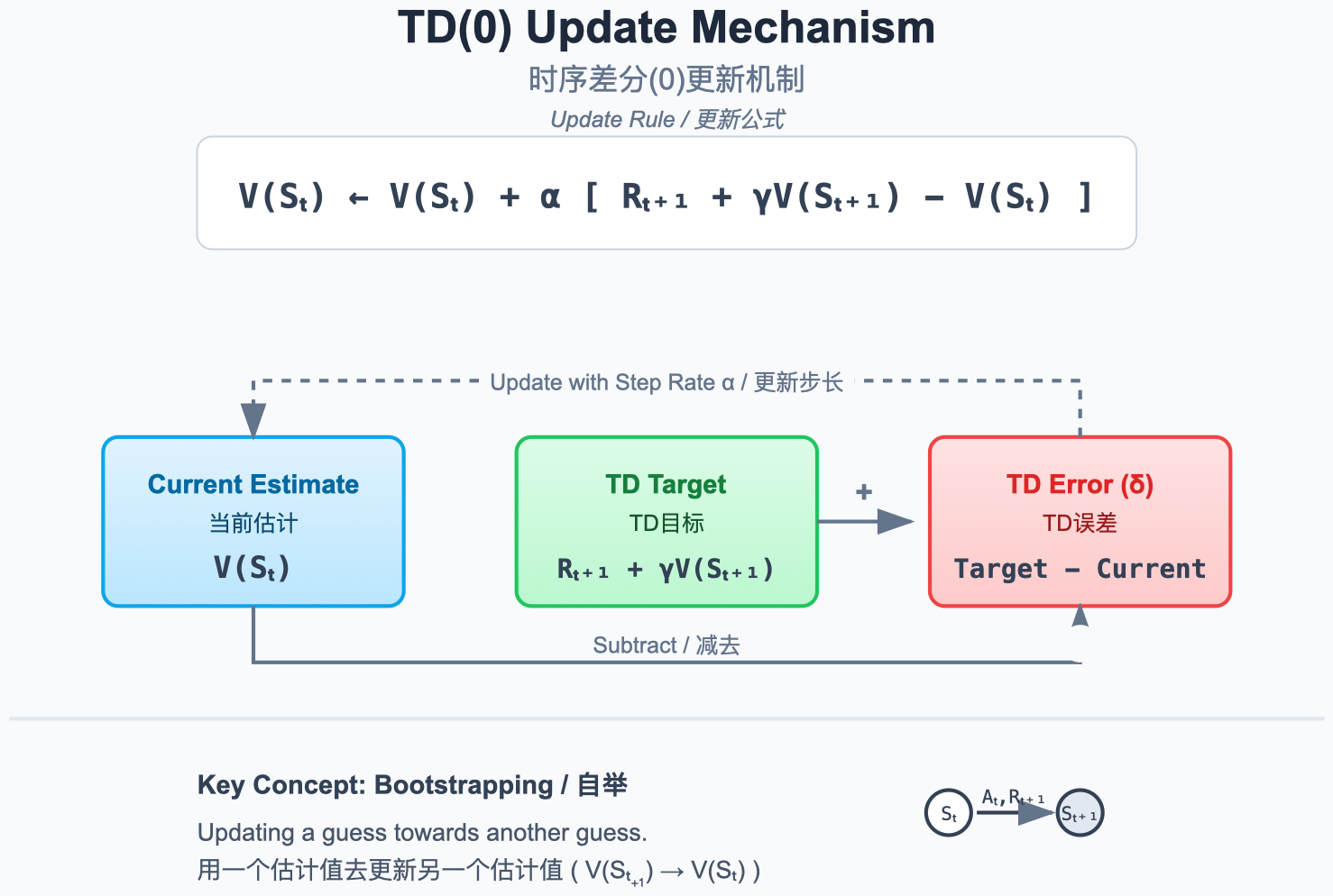
图解说明：

在状态 S t S_t St 执行动作后，观察到奖励 r t + 1 r_{t+1} rt+1 和下一状态 S t + 1 S_{t+1} St+1。

用 r t + 1 + γ V ( S t + 1 ) r_{t+1} + \gamma V(S_{t+1}) rt+1+γV(St+1) 作为目标值（TD Target），更新 V ( S t ) V(S_t) V(St)。

这就是 Bootstrapping（自举）：用估计值更新估计值。

更新公式：

V ( S t ) ← V ( S t ) + α [ r t + 1 + γ V ( S t + 1 ) ⏞ TD Target（TD 目标） − V ( S t ) ] ⏟ TD Error（TD 误差） δ t V(S_t) \leftarrow V(S_t) + \alpha \underbrace{\left[ \overbrace{r_{t+1} + \gamma V(S_{t+1})}^{\text{TD Target（TD 目标）}} - V(S_t) \right]}_{\text{TD Error（TD 误差）} \delta_t} V(St)←V(St)+αTD Error（TD 误差）δt rt+1+γV(St+1) TD Target（TD 目标）−V(St)

三个关键概念：

TD Target（TD 目标） ： r t + 1 + γ V ( S t + 1 ) r_{t+1} + \gamma V(S_{t+1}) rt+1+γV(St+1)，是对真实回报 G t G_t Gt 的一步近似。
TD Error（TD 误差） ： δ t = r t + 1 + γ V ( S t + 1 ) − V ( S t ) \delta_t = r_{t+1} + \gamma V(S_{t+1}) - V(S_t) δt=rt+1+γV(St+1)−V(St)，衡量"预期"与"现实"的差距。
学习率 α \alpha α ：控制更新步长。 α \alpha α 越大更新越激进，越小越保守。

代码实现 (TD(0) 预测)

python 复制代码

from collections import defaultdict

def td_0_prediction(env, policy, num_episodes=1000, alpha=0.1, gamma=0.99):
    """TD(0) 策略评估

    Args:
        env: 环境对象
        policy: 策略字典 {state: action}
        num_episodes: 训练轮数
        alpha: 学习率
        gamma: 折扣因子
    """
    V = defaultdict(float)

    for episode in range(num_episodes):
        state = env.reset()
        while True:
            action = policy[state]
            next_state, reward, done = env.step(state, action)

            # TD 更新：核心一行代码
            td_target = reward + gamma * V[next_state] * (1 - done)
            td_error = td_target - V[state]
            V[state] += alpha * td_error

            state = next_state
            if done:
                break
    return V

与 MC 的代码对比 ：MC 需要先收集完整轨迹，再反向计算回报；TD(0) 在 while 循环内部就完成了更新，无需存储轨迹。

4. n-step TD

TD(0) 只看一步就更新，MC 要看完全部。n-step TD 是介于两者之间的折中------向前看 n 步。

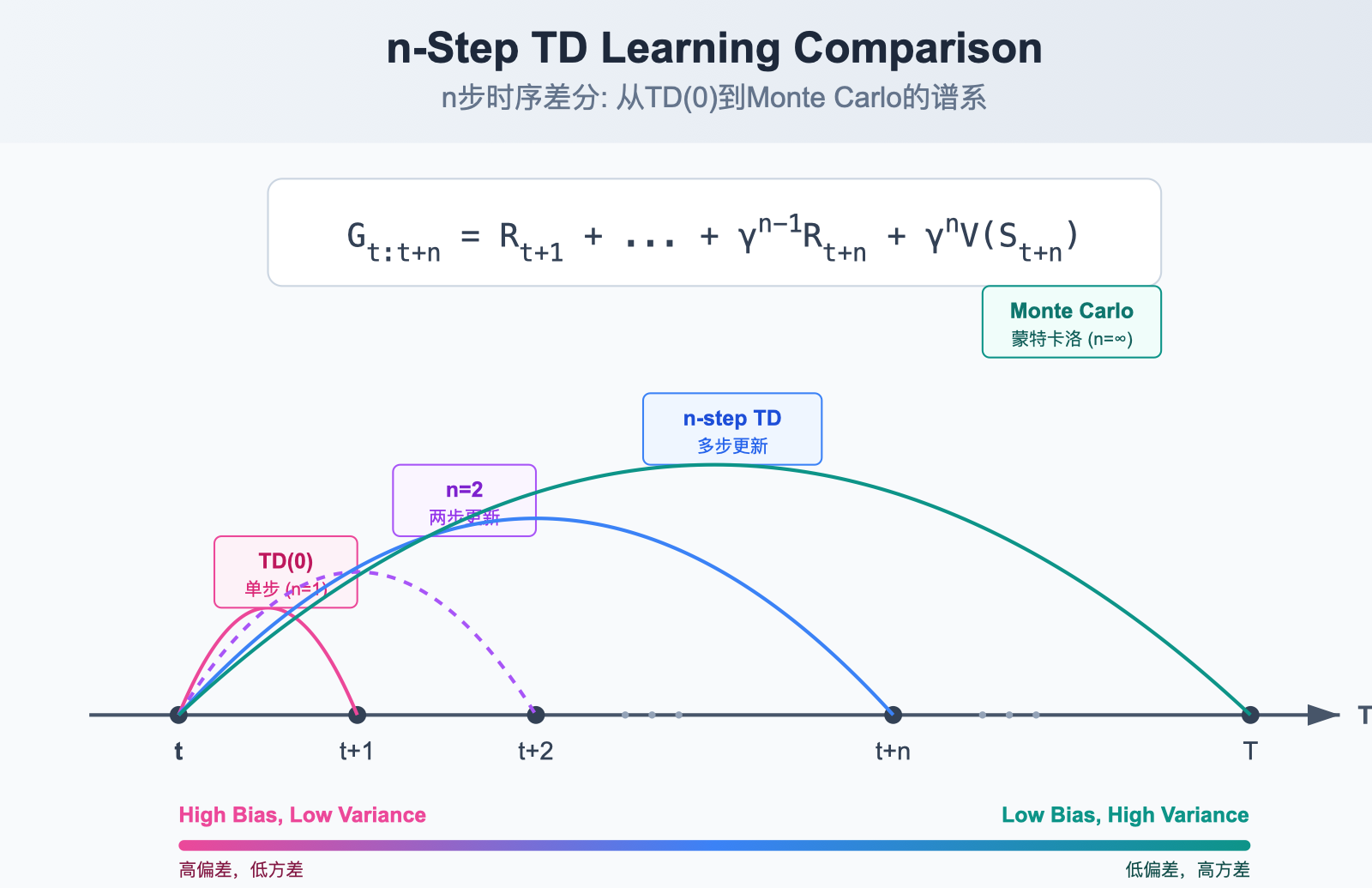
图解说明：

n=1 (TD(0))：只看一步奖励，剩余用估计值补全。偏差大，方差小。

n=中间值：平衡偏差与方差。

n=∞ (MC)：看完整条轨迹，无偏但方差大。

n-step 回报 (n-step Return)：

G t ( n ) = r t + 1 + γ r t + 2 + γ 2 r t + 3 + ⋯ + γ n − 1 r t + n + γ n V ( S t + n ) G_t^{(n)} = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \dots + \gamma^{n-1} r_{t+n} + \gamma^n V(S_{t+n}) Gt(n)=rt+1+γrt+2+γ2rt+3+⋯+γn−1rt+n+γnV(St+n)

各 n 值对应的回报公式：

n	回报公式	特点
1	G t ( 1 ) = r t + 1 + γ V ( S t + 1 ) G_t^{(1)} = r_{t+1} + \gamma V(S_{t+1}) Gt(1)=rt+1+γV(St+1)	TD(0)，偏差最大
2	G t ( 2 ) = r t + 1 + γ r t + 2 + γ 2 V ( S t + 2 ) G_t^{(2)} = r_{t+1} + \gamma r_{t+2} + \gamma^2 V(S_{t+2}) Gt(2)=rt+1+γrt+2+γ2V(St+2)	稍低偏差
n	G t ( n ) = ∑ k = 1 n γ k − 1 r t + k + γ n V ( S t + n ) G_t^{(n)} = \sum_{k=1}^{n} \gamma^{k-1} r_{t+k} + \gamma^n V(S_{t+n}) Gt(n)=∑k=1nγk−1rt+k+γnV(St+n)	通用形式
∞	G t ( ∞ ) = ∑ k = 1 T − t γ k − 1 r t + k G_t^{(\infty)} = \sum_{k=1}^{T-t} \gamma^{k-1} r_{t+k} Gt(∞)=∑k=1T−tγk−1rt+k	MC，无偏

更新规则：

V ( S t ) ← V ( S t ) + α [ G t ( n ) − V ( S t ) ] V(S_t) \leftarrow V(S_t) + \alpha \left[ G_t^{(n)} - V(S_t) \right] V(St)←V(St)+α[Gt(n)−V(St)]

代码实现 (n-step TD)

python 复制代码

def n_step_td(env, policy, n=4, num_episodes=1000, alpha=0.1, gamma=0.99):
    """n-step TD 预测"""
    V = defaultdict(float)

    for _ in range(num_episodes):
        state = env.reset()
        states = [state]
        rewards = [0]  # rewards[0] 占位

        T = float('inf')  # Episode 终止时间
        t = 0

        while True:
            if t < T:
                action = policy[states[t]]
                next_state, reward, done = env.step(states[t], action)
                states.append(next_state)
                rewards.append(reward)
                if done:
                    T = t + 1

            tau = t - n + 1  # 被更新的状态时刻
            if tau >= 0:
                # 计算 n-step 回报
                G = sum(gamma**(i - tau - 1) * rewards[i]
                        for i in range(tau + 1, min(tau + n, T) + 1))
                if tau + n < T:
                    G += gamma**n * V[states[tau + n]]

                V[states[tau]] += alpha * (G - V[states[tau]])

            if tau == T - 1:
                break
            t += 1

    return V

实验结论 (Sutton & Barto)：在 19-state Random Walk 任务上，n 取中间值（如 n=4）时误差最小，说明折中方案优于极端的 TD(0) 或 MC。

5. TD(λ) 与资格迹

n-step TD 需要选定一个 n，不同任务的最优 n 不同。TD(λ) 巧妙地将所有 n-step 回报按指数衰减权重进行加权平均，一次性涵盖所有 n。

5.1 λ-回报 (Forward View / 前向视角)

G t λ = ( 1 − λ ) ∑ n = 1 T − t − 1 λ n − 1 G t ( n ) + λ T − t − 1 G t G_t^\lambda = (1-\lambda) \sum_{n=1}^{T-t-1} \lambda^{n-1} G_t^{(n)} + \lambda^{T-t-1} G_t Gtλ=(1−λ)n=1∑T−t−1λn−1Gt(n)+λT−t−1Gt

λ = 0 \lambda = 0 λ=0 时，退化为 TD(0)
λ = 1 \lambda = 1 λ=1 时，退化为 MC

直觉：对每种"看几步"的方案都投一票，但更信任"看得少"的方案（因为方差小）。 λ \lambda λ 控制衰减速度。

5.2 资格迹 (Backward View / 后向视角)

前向视角需要等到 Episode 结束才能计算。后向视角引入资格迹 (Eligibility Traces) 实现在线更新。

资格迹回答一个关键问题："谁该为当前的 TD Error 负责？"

E t ( s ) = γ λ E t − 1 ( s ) + 1 ( S t = s ) E_t(s) = \gamma \lambda E_{t-1}(s) + \mathbb{1}(S_t=s) Et(s)=γλEt−1(s)+1(St=s)

两个启发式原则：

频率启发 (Frequency Heuristic) ：访问越频繁的状态，责任越大 → 1 ( S t = s ) \mathbb{1}(S_t=s) 1(St=s) 累加。
时近启发 (Recency Heuristic) ：越近访问的状态，责任越大 → γ λ \gamma \lambda γλ 衰减。

5.3 前向视角 vs 后向视角

特性	前向视角 (Forward View)	后向视角 (Backward View)
核心概念	λ-回报 G t λ G_t^\lambda Gtλ	资格迹 E t ( s ) E_t(s) Et(s)
更新方向	向前看：加权所有 n-step 回报	向后看：TD Error 传播给所有"有责"状态
在线性	否，需等 Episode 结束	是，每步可更新
等价关系	离线更新时二者严格等价
实际使用	概念理解用	实际实现用

代码实现 (TD(λ) 资格迹)

python 复制代码

def td_lambda(env, policy, num_episodes=1000, alpha=0.1, gamma=0.99, lambd=0.8):
    """TD(λ) with Eligibility Traces (后向视角实现)"""
    V = defaultdict(float)

    for _ in range(num_episodes):
        state = env.reset()
        E = defaultdict(float)  # 资格迹，每 Episode 重置

        while True:
            action = policy[state]
            next_state, reward, done = env.step(state, action)

            # 1. 计算 TD Error
            td_error = reward + gamma * V[next_state] * (1 - done) - V[state]

            # 2. 累积当前状态的资格 (Accumulating Traces)
            E[state] += 1

            # 3. 更新所有"有责"状态（后向传播 TD Error）
            for s in list(E.keys()):
                V[s] += alpha * td_error * E[s]
                E[s] *= gamma * lambd   # 资格衰减
                if E[s] < 1e-5:
                    del E[s]  # 清除微小资格，提升效率

            state = next_state
            if done:
                break

    return V

资格迹的三种变体：

累积迹 (Accumulating) ： E t ( s ) = γ λ E t − 1 ( s ) + 1 E_t(s) = \gamma \lambda E_{t-1}(s) + 1 Et(s)=γλEt−1(s)+1，多次访问会叠加。
替换迹 (Replacing) ： E t ( s ) = 1 E_t(s) = 1 Et(s)=1（访问时直接置 1），避免过度累积。
Dutch 迹 ： E t ( s ) = ( 1 − α ) γ λ E t − 1 ( s ) + 1 E_t(s) = (1-\alpha) \gamma \lambda E_{t-1}(s) + 1 Et(s)=(1−α)γλEt−1(s)+1，考虑学习率影响。

6. 回溯更新图解 (Backup Diagram)

"Backup"在 RL 中是专业术语，意为回溯更新------用未来状态的信息回溯更新当前状态的价值。

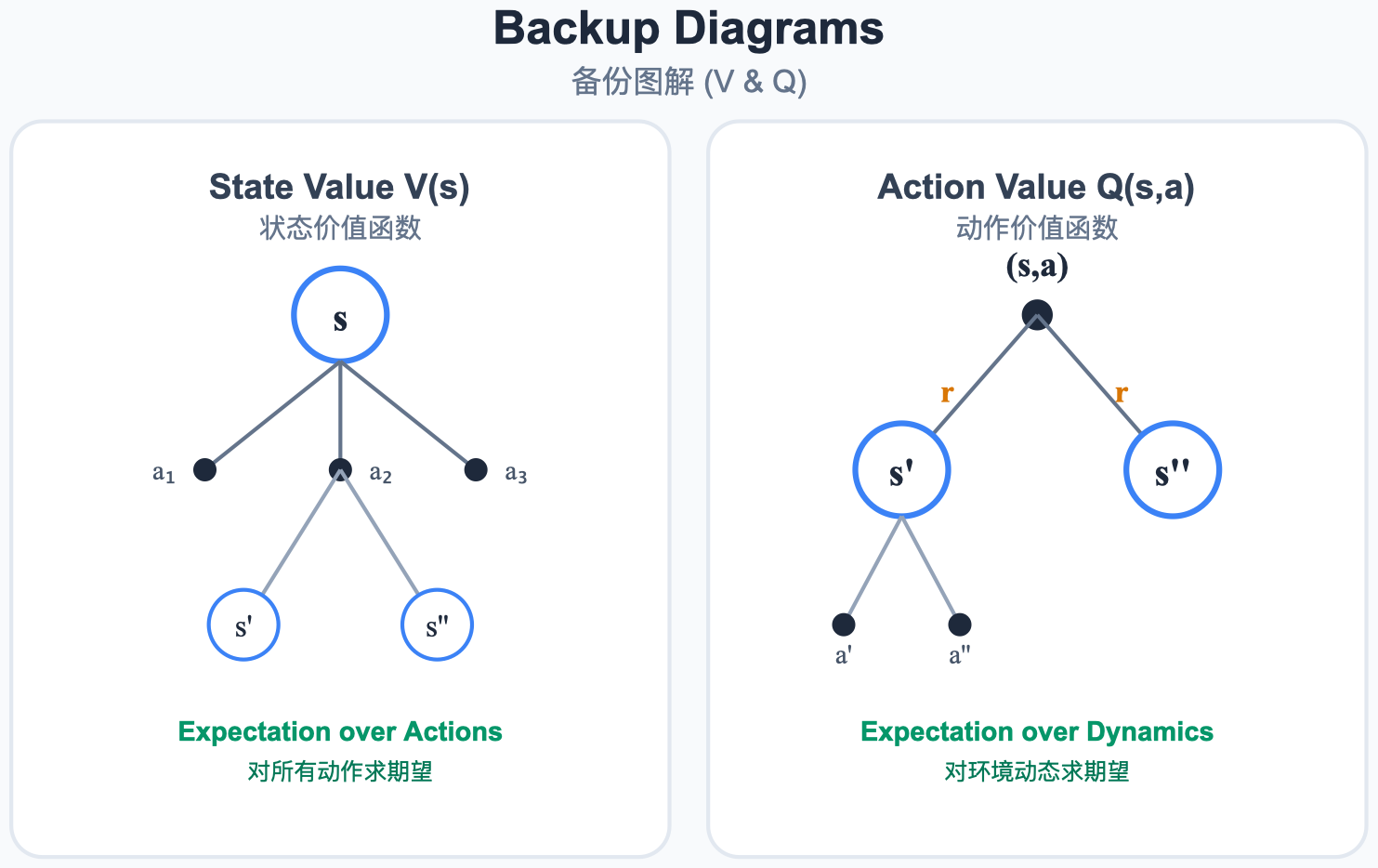
图解说明：

MC 回溯更新：必须走到 Episode 终点，采样整条轨迹，然后用真实回报更新起点。

TD 回溯更新 ：只向前走一步，用 r + γ V ( S ′ ) r + \gamma V(S') r+γV(S′) 来近似未来价值，立即更新。

DP 回溯更新 (Full Backup)：不需要采样，利用已知的环境模型计算所有可能后继状态的期望值。

三种方法的回溯更新对比：

方法	采样	自举	回溯深度	需要模型
DP	否 (Full Backup)	是	1 步	是
MC	是 (Sample Backup)	否	完整轨迹	否
TD	是 (Sample Backup)	是	1~n 步	否

7. 偏差-方差权衡

这是 TD 学习中最重要的理论问题之一。

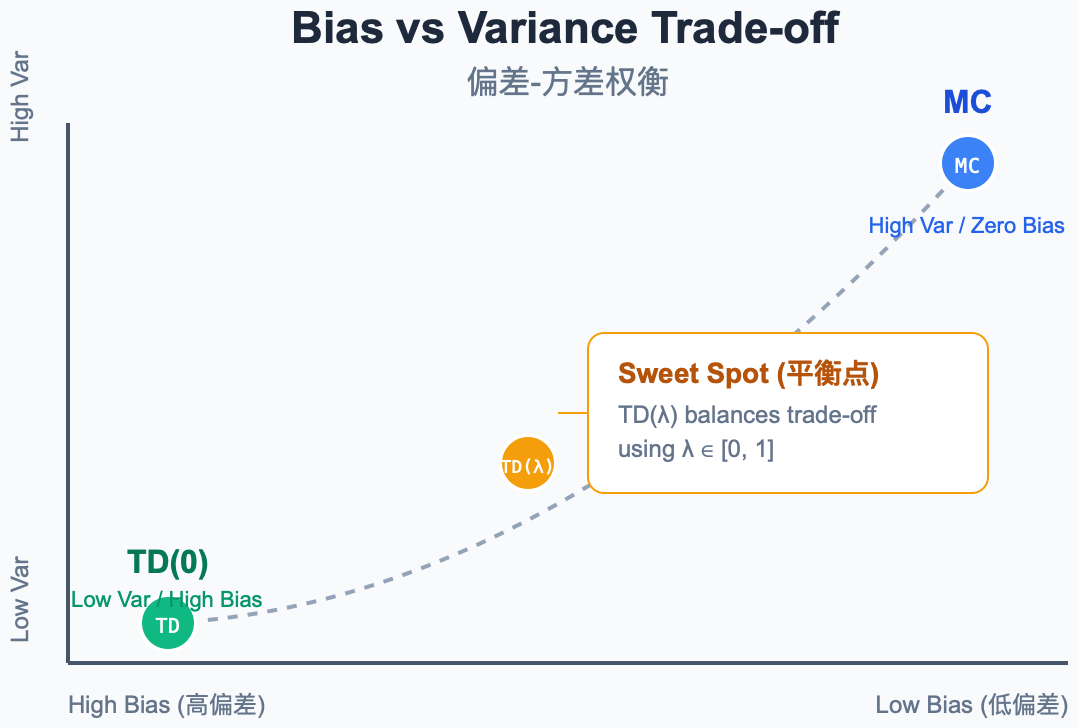
图解说明：

MC 端 (高方差，零偏差)：使用真实回报，无偏但受轨迹随机性影响大。

TD 端 (低方差，有偏差)：使用估计值自举，方差小但引入偏差。

TD(λ) ：通过 λ \lambda λ 在两端之间平滑过渡。

7.1 为什么 MC 方差高？

MC 的目标是 G t = r t + 1 + γ r t + 2 + ⋯ + γ T − t − 1 r T G_t = r_{t+1} + \gamma r_{t+2} + \dots + \gamma^{T-t-1} r_T Gt=rt+1+γrt+2+⋯+γT−t−1rT。

回报 G t G_t Gt 受 ( T − t ) (T-t) (T−t) 步随机性影响：每一步的状态转移、动作选择、奖励都是随机的。步数越多，累积方差越大。

7.2 为什么 TD 偏差大？

TD Target = r t + 1 + γ V ( S t + 1 ) = r_{t+1} + \gamma V(S_{t+1}) =rt+1+γV(St+1)，其中 V ( S t + 1 ) V(S_{t+1}) V(St+1) 是估计值。

如果估计不准确，TD Target 就是有偏的。但好消息是：随着学习的进行， V V V 逐渐趋于准确，偏差逐渐消失（渐近无偏）。

7.3 实际选择建议

场景	推荐方法	原因
数据稀缺	TD	方差低，数据效率高
非终止任务	TD	MC 无法处理
需要无偏估计	MC	理论保证
折中方案	TD(λ)	灵活调节

8. TD 学习的收敛性

TD(0) 的收敛保证：

在满足以下条件时，TD(0) 收敛到真实价值 V π V^\pi Vπ：

所有状态被无限次访问
学习率满足 Robbins-Monro 条件： ∑ t α t = ∞ \sum_t \alpha_t = \infty ∑tαt=∞， ∑ t α t 2 < ∞ \sum_t \alpha_t^2 < \infty ∑tαt2<∞

TD 与 MC 的收敛行为差异：

MC ：最小化均方误差 (MSE)， min ⁡ V ∑ s [ V ( s ) − E [ G t ∣ S t = s ] ] 2 \min_V \sum_s \left[ V(s) - \mathbb{E}[G_t | S_t=s] \right]^2 minV∑s[V(s)−E[Gt∣St=s]]2
TD(0)：收敛到最大似然马尔可夫模型的精确解，在有限数据下通常更好

TD 的确定性等价估计 (Certainty Equivalence)：TD(0) 实际上隐含地构建了一个 MDP 模型，然后求解该模型。这意味着 TD 能更好地利用马尔可夫性质。

9. 总结与预告

本章核心：

TD Learning：结合 MC 的采样与 DP 的自举，不用等到终止就能每步更新。
TD Error ( δ t \delta_t δt) ： r + γ V ( S ′ ) − V ( S ) r + \gamma V(S') - V(S) r+γV(S′)−V(S)，衡量"预期与现实的差距"，贯穿整个 RL。
n-step TD：看 n 步再更新，在偏差与方差之间灵活折中。
TD( λ \lambda λ) 与资格迹：加权所有 n-step 回报，用资格迹高效回答"谁该为这次惊喜负责"。

TD Error 在现代 RL 中的地位

TD Error δ t \delta_t δt 不仅是本章的核心，更贯穿整个强化学习：

Actor-Critic：TD Error 作为 Critic 给 Actor 的"打分"
GAE：对 TD Error 做指数加权平均来估计优势函数
神经科学：大脑多巴胺信号与 TD Error 高度相似（2024 年 Barto 综述）

下一章预告 ：

目前我们只讨论了预测 (Prediction) ，即评估一个给定的策略。如何进行控制 (Control) ，即找到最优策略？下一章将介绍 Q-Learning 和 SARSA------两种经典的 TD 控制算法。

➡️ 下一章：第 6 章 Q-Learning 与 SARSA