抗量子 Winternitz One Time Signature（OTS）算法学习

参考blog

bash 复制代码

https://accu.cc/content/cryptography/winternitz/

原理

Winternitz OTS 算法也是一种基于hash的具有抗量子性能的算法。

其数学上的核心原理也非常简单：假设我们使用的hash是sha256，对某一段数据hash c次的结果等价于先对这段数据hash a 次，再hash b 次。其中 a + b = c

bash 复制代码

M：message
# a + b = c
rslt = hash(M)^c
temp_a = hash(M) ^a
temp_rslt = hash(temp_a)^b
rslt == temp_rslt

更具体来说，将我们需要签名的消息（M）以N （N = 2,4,8,...,256,...）为单位，划分出若干个chunk，这个chunk 被视作一个数字 number。比如我们的M一共有256 bit，取N = 8，则我们可以得到32 个number，每个number 大小在0 - 255 之间。后续的操作跟数学原理相结合会更好解释，因此直接进入到算法流程。

算法流程

假设：M一共有256 bit，取N = 8，则我们可以得到32 个chunk，取c = 256。我们总是对原文进行操作

密钥生成

先生成32 个 256 bit 的随机数，将这32个随机数作为我们的私钥（sk）
将这32把私钥，反复做256/c 次 hash，计算出来的结果作为我们的公钥（pk）

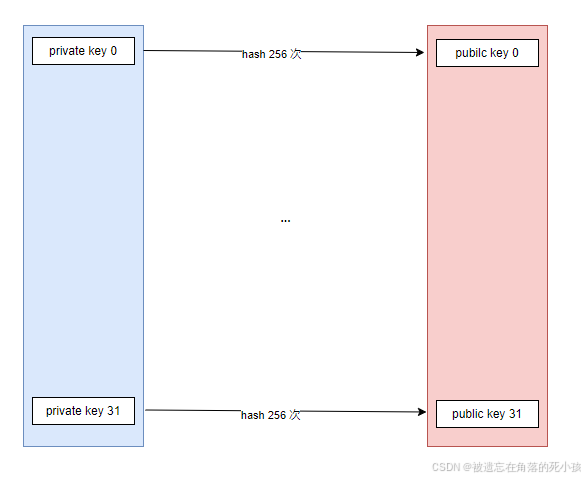
至此，W-OTS 算法的密钥生成部分结束

签名生成

将M hash一次，得到对应的结果Hash
将Hash 拆成32个 chunk，每个chunk表示一个数字，number
对chunk hash （256 - number） 次，得到的结果作为签名的一部分。例如：chunk0 是 0110_1111，则number 是十进制的111，所以我们对chunk0 hash 256 - 111 = 145 次
对所有chunk 做完上述两步操作后，将其结果拼接起来，最后就得到了我们的签名

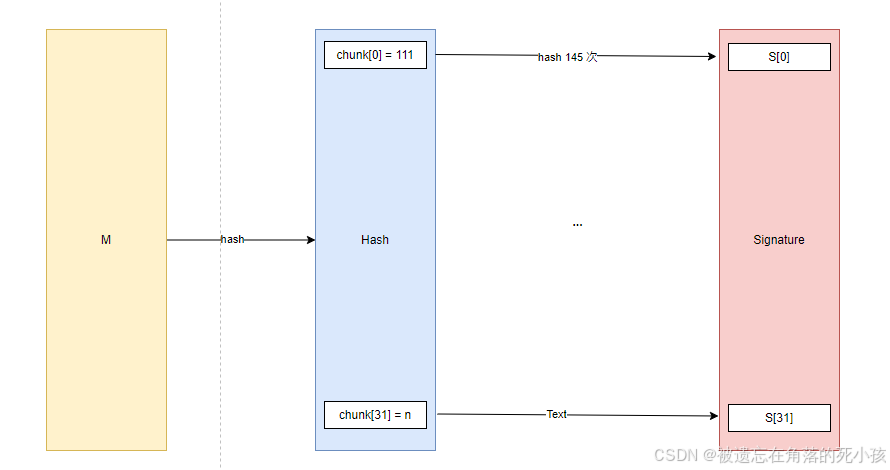
签名验证

将M进行一次hash操作，得到的结果为：Hash，大小为256 bit
将Hash 拆成32 个chunk，chunk的值为number
对签名S 以256 bit（只是sha 256的运算结果为256bit）的大小进行划分，这样划分出来的item有32个，对这些item hash number 次，得到的结果为 rslt_set
判断rslt_set 是否与公钥pk 相等，如果都相等，代表验签无误。否则验签失败

弊端

与Lamport OTS 不同，Winternitz OTS 不会暴露出私钥，而且签名的大小会有所减少，但是会需要更多的hash 次数。而且hash 次数越多，并不会提升安全性，真正的安全性还是与hash 本身有关

抗量子 Winternitz One Time Signature（OTS） 算法学习