FA:formulas and algorithm,PC:planning and control
一、A * 算法核心概念
A * 是一种启发式搜索算法,结合了 Dijkstra 算法(保证最优)和贪心算法(搜索高效)的优点,核心思想是:
- 对每个待探索的节点,计算一个评估函数 f(n)f(n)f(n),以此决定搜索优先级;
- 优先搜索f(n)f(n)f(n)最小的节点,最终以最小代价找到从起点到终点的最优路径。
1. 核心评估函数
f(n)=g(n)+h(n)f(n)=g(n)+h(n)f(n)=g(n)+h(n)
- g(n)g(n)g(n):从起点 到当前节点nnn的实际代价(已走路径的真实长度);
- h(n)h(n)h(n):从当前节点n到终点 的估计代价(启发函数,关键!);
- f(n)f(n)f(n):从起点经过节点n到终点的总估计代价。
2. 启发函数(h(n)h (n)h(n))的选择
启发函数的设计直接决定 A * 的性能:
表格
| 启发函数类型 | 公式(二维网络) | 特点 |
|---|---|---|
| 曼哈顿距离 | h(n)=xn−xgoal+yn−ygoalh(n)=x_n-x_{goal}+y_n-y_{goal}h(n)=xn−xgoal+yn−ygoal | 适用于只能上下左右移动的网格(无对角线) |
| 欧几里得距离 | h(n)=(xn−xgoal2+(yn−ygoal)2)h(n)=\sqrt{(x_n-x_{goal}^2+(y_n−y_{goal})^2)}h(n)=(xn−xgoal2+(yn−ygoal)2) | 适用于可任意方向移动的场景(如机器人路径规划) |
| 切比雪夫距离 | h(n)=max(xn−xgoal,yn−ygoal)h(n)=max(x_n-x_{goal},y_n-y_{goal})h(n)=max(xn−xgoal,yn−ygoal) | 适用于可对角线移动的网格 |
关键规则:
- h(n)h(n)h(n)必须是可采纳的(admissible):即h(n)≤h(n)≤h(n)≤ 节点n到终点的真实代价,这样才能保证 A * 找到最优路径;
若h(n)=0h(n)=0h(n)=0,A * 退化为 Dijkstra 算法(搜索全图,效率低);
若h(n)h(n)h(n)过大(超过真实代价),A * 可能找不到最优路径,但搜索速度更快。
3. 核心数据结构
- 开放列表(Open List):存储待探索的节点,按f(n)从小到大排序;
- 关闭列表(Closed List):存储已探索完成的节点,避免重复搜索。
二、A * 算法的使用场景
A * 因 "最优 + 高效" 的特性,是路径规划领域的首选算法,主要应用场景:
- 游戏开发:游戏角色 / NPC 的路径寻路(如《王者荣耀》《我的世界》的角色移动);
- 移动机器人:AGV、扫地机器人、无人机的全局路径规划(已知环境地图);
- 自动驾驶:高精度地图下的全局路径规划(如从 A 点到 B 点的最优道路选择);
- 物流 / 仓储:无人叉车、分拣机器人的路径规划;
- 地图导航:高德 / 百度地图的步行 / 驾车路径规划(底层核心算法之一)。
优势:
- 保证找到最优路径(当h(n)h(n)h(n)可采纳时);
- 搜索效率远高于 Dijkstra 算法(启发函数减少无效搜索);
- 逻辑清晰,易于实现和扩展。
局限性:
- 依赖完整的环境地图(无法处理未知环境);
- 内存消耗较大(需存储开放 / 关闭列表);
- 对动态障碍物适配性差(需重新规划)。
三、A * 算法的具体操作步骤
以二维平面(连续空间)的机器人路径规划为例,核心步骤如下:
步骤 1:初始化
- 定义起点SSS、终点GGG、障碍物区域;
- 初始化开放列表(仅加入起点SSS,计算f(S)=g(S)+h(S)f(S)=g(S)+h(S)f(S)=g(S)+h(S),其中g(S)=0g(S)=0g(S)=0);
- 初始化关闭列表(空);
- 为每个节点记录父节点(用于回溯路径)。
步骤 2:循环搜索
- 从开放列表中取出f(n)最小的节点n(当前节点);
- 将节点n从开放列表移至关闭列表;
- 若节点n是终点G,回溯父节点得到完整路径,结束算法;
- 生成节点n的相邻节点(如上下左右 / 周围采样点);
- 对每个相邻节点m:
- 若m在障碍物区域 / 关闭列表中,跳过;
- 计算g(m)=g(n)+节点n到mg(m) = g(n) +节点n到mg(m)=g(n)+节点n到m的实际距离;
- 若m不在开放列表中:
- 计算h(m)h(m)h(m)(如欧几里得距离),f(m)=g(m)+h(m)f(m)=g(m)+h(m)f(m)=g(m)+h(m);
- 将m加入开放列表,记录父节点为n;
若m已在开放列表中: - 若新的g(m)更小(说明有更优路径到达m),更新g(m)、f(m),并将m的父节点改为n;
- 重复步骤 2,直到开放列表为空(无路径)或找到终点。
步骤 3:路径回溯
从终点GGG开始,依次回溯父节点,直到起点SSS,反转后得到完整路径。
四、A * 算法代码实现(二维连续空间)
以下是适配机器人路径规划的 A * 代码(连续空间,非网格),包含可视化功能,可直接运行:
bash
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
import math
# 定义节点类(存储位置、代价、父节点)
class Node:
def __init__(self, x, y):
self.x = x # 节点x坐标
self.y = y # 节点y坐标
self.g = 0.0 # 起点到当前节点的实际代价
self.h = 0.0 # 当前节点到终点的估计代价
self.f = 0.0 # 总代价 f = g + h
self.parent = None # 父节点(用于回溯路径)
def __eq__(self, other):
# 重载相等判断,用于检查节点是否已存在
if isinstance(other, Node):
return (self.x == other.x) and (self.y == other.y)
return False
# 定义A*规划器类
class AStarPlanner:
def __init__(self):
self.step_size = 0.5 # 相邻节点的步长(控制搜索精度)
self.obstacle_radius = 1.0 # 障碍物影响半径
self.max_iter = 5000 # 最大迭代次数(防止死循环)
# 启发函数:欧几里得距离(可采纳,保证最优)
def heuristic(self, node, goal_node):
return math.hypot(node.x - goal_node.x, node.y - goal_node.y)
# 检查节点是否在障碍物区域内
def is_collision(self, node, obstacles):
for (ox, oy) in obstacles:
if math.hypot(node.x - ox, node.y - oy) < self.obstacle_radius:
return True
return False
# 生成当前节点的相邻节点(8方向采样)
def generate_neighbors(self, current_node):
neighbors = []
# 8个方向的偏移量(上下左右+对角线)
directions = [
(self.step_size, 0), (-self.step_size, 0),
(0, self.step_size), (0, -self.step_size),
(self.step_size, self.step_size), (-self.step_size, -self.step_size),
(self.step_size, -self.step_size), (-self.step_size, self.step_size)
]
for dx, dy in directions:
x = current_node.x + dx
y = current_node.y + dy
# 限制坐标范围(可选,防止节点超出地图)
if 0 <= x <= 10 and 0 <= y <= 10:
neighbors.append(Node(x, y))
return neighbors
# 从开放列表中找到f值最小的节点
def find_min_f_node(self, open_list):
min_node = open_list[0]
for node in open_list:
if node.f < min_node.f:
min_node = node
return min_node
# 规划路径
def plan(self, start_pos, goal_pos, obstacles):
# 初始化起点和终点节点
start_node = Node(start_pos[0], start_pos[1])
goal_node = Node(goal_pos[0], goal_pos[1])
# 初始化开放列表和关闭列表
open_list = [start_node]
closed_list = []
iter_count = 0
while open_list and iter_count < self.max_iter:
iter_count += 1
# 步骤1:取出f值最小的节点
current_node = self.find_min_f_node(open_list)
open_list.remove(current_node)
closed_list.append(current_node)
# 步骤2:检查是否到达终点
if current_node == goal_node:
# 回溯路径
path = []
while current_node is not None:
path.append((current_node.x, current_node.y))
current_node = current_node.parent
# 反转路径(从起点到终点)
return path[::-1]
# 步骤3:生成相邻节点
neighbors = self.generate_neighbors(current_node)
for neighbor in neighbors:
# 跳过碰撞节点和已探索节点
if self.is_collision(neighbor, obstacles) or neighbor in closed_list:
continue
# 计算g值(当前节点到相邻节点的实际距离)
tentative_g = current_node.g + math.hypot(
neighbor.x - current_node.x, neighbor.y - current_node.y
)
# 情况1:相邻节点不在开放列表中
if neighbor not in open_list:
neighbor.g = tentative_g
neighbor.h = self.heuristic(neighbor, goal_node)
neighbor.f = neighbor.g + neighbor.h
neighbor.parent = current_node
open_list.append(neighbor)
# 情况2:相邻节点已在开放列表中,检查是否有更优路径
else:
# 找到开放列表中的对应节点
for open_node in open_list:
if open_node == neighbor:
if tentative_g < open_node.g:
open_node.g = tentative_g
open_node.f = open_node.g + open_node.h
open_node.parent = current_node
break
# 若迭代结束仍未找到路径
print("警告:未找到有效路径!")
return []
# -------------------------- 测试代码 --------------------------
if __name__ == "__main__":
# 1. 初始化A*规划器
a_star = AStarPlanner()
# 2. 设置起点、终点、障碍物
start = (0.0, 0.0) # 起点
goal = (8.0, 8.0) # 终点
obstacles = [ # 障碍物列表
(3.0, 3.0),
(5.0, 5.0),
(7.0, 3.0)
]
# 3. 规划路径
path = a_star.plan(start, goal, obstacles)
# 4. 可视化结果
plt.figure(figsize=(8, 8))
# 绘制障碍物
for (ox, oy) in obstacles:
circle = Circle((ox, oy), a_star.obstacle_radius, color='r', alpha=0.3, label='Obstacle' if (ox, oy) == obstacles[0] else "")
plt.gca().add_patch(circle)
# 绘制路径
if path:
path_x = [p[0] for p in path]
path_y = [p[1] for p in path]
plt.plot(path_x, path_y, 'b-', linewidth=2, label='A* Path')
# 绘制起点和终点
plt.scatter(start[0], start[1], color='green', s=100, label='Start')
plt.scatter(goal[0], goal[1], color='red', s=100, label='Goal')
# 图表设置
plt.xlabel('X (m)')
plt.ylabel('Y (m)')
plt.title('A* Path Planning')
plt.legend(loc='upper left') # 图例放左上角
plt.grid(True)
plt.axis('equal')
plt.xlim(0, 10)
plt.ylim(0, 10)
plt.show()五、代码关键部分解释
1. 节点类(Node)
存储节点的核心信息:坐标(x,y)、代价(g/h/f)、父节点(用于路径回溯),重载__eq__方法方便判断节点是否重复。
2. 核心方法
- heuristic:计算欧几里得距离作为启发函数(可采纳,保证最优);
- is_collision:检查节点是否在障碍物范围内(避免碰撞);
- generate_neighbors:生成当前节点的 8 方向相邻节点(控制搜索范围);
- find_min_f_node:从开放列表中找到f(n)最小的节点(核心搜索逻辑);
- plan:主规划函数,实现 A * 的完整搜索流程。
3. 运行前置条件
安装依赖:
bash
pip install numpy matplotlib4. 运行效果
- 代码会绘制出从(0,0)到(8,8)的最优路径,绕过(3,3)、(5,5)、(7,3)三个障碍物;
- 路径是连续的坐标点,可直接用于机器人的运动控制;
- 图例默认放在左上角(符合你之前的要求)。
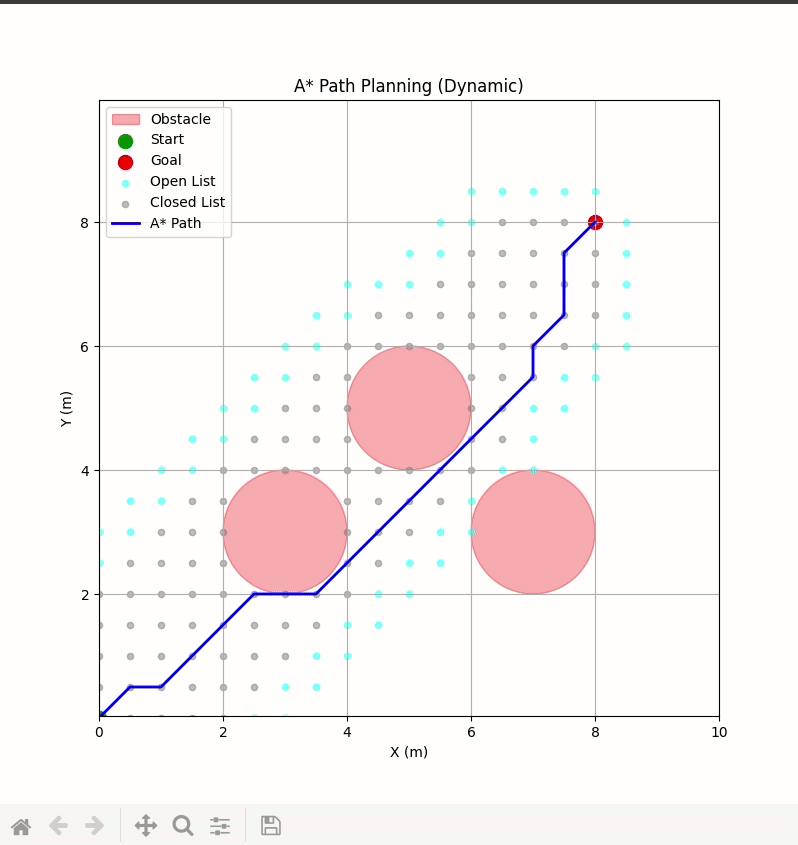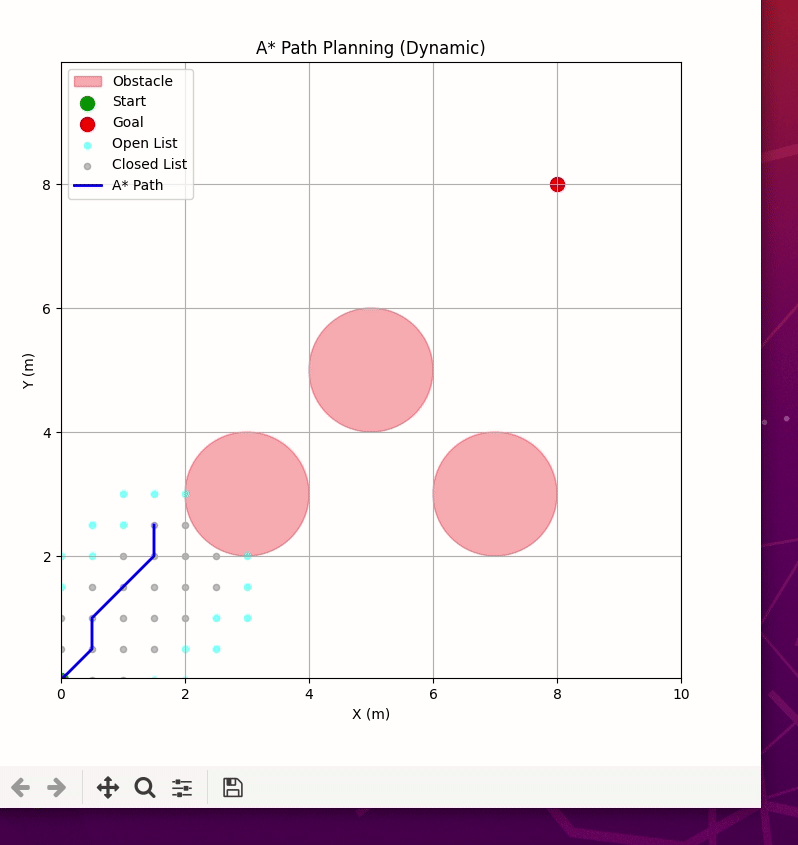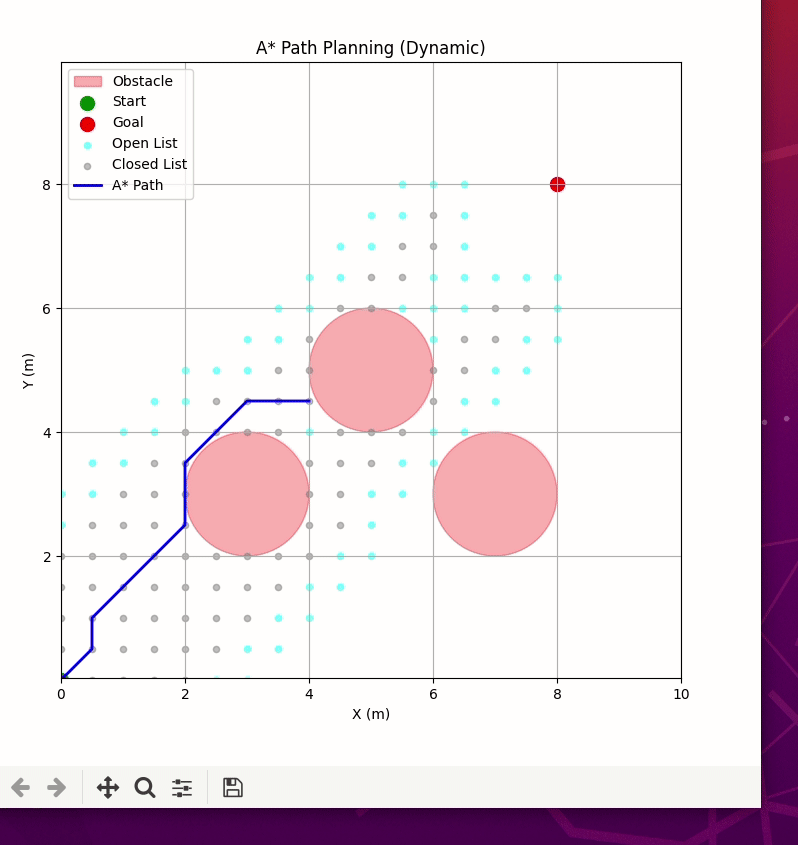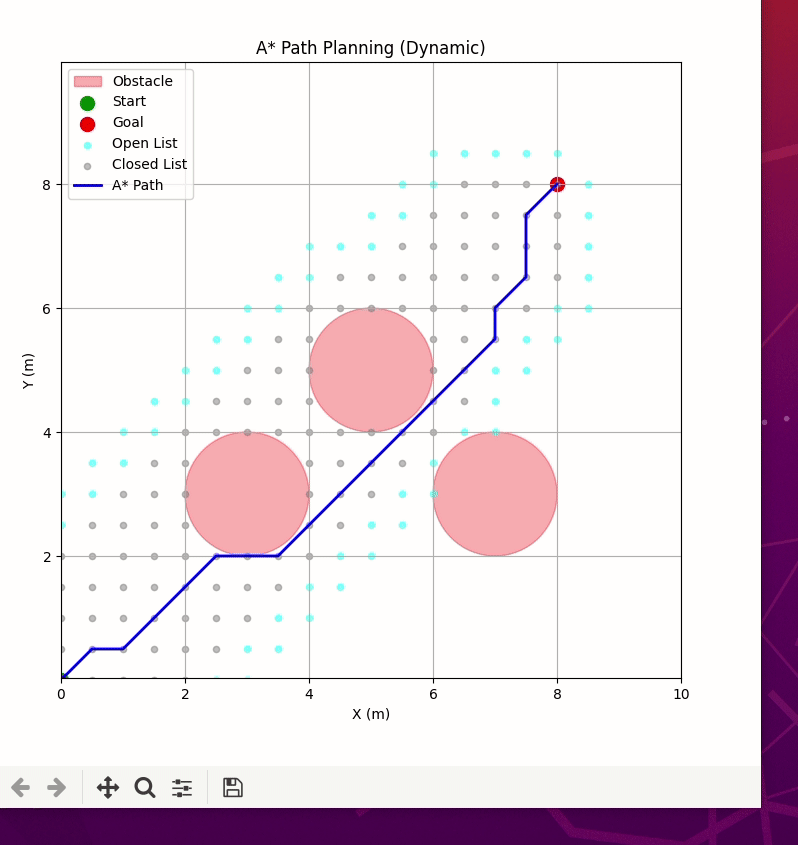
六、A* vs APF(人工势场法)
表格
| 特性 | A * 算法 | APF 算法 |
|---|---|---|
| 路径最优性 | 保证最优(h (n) 可采纳时) | 不一定最优,易陷入局部最小值 |
| 环境要求 | 需完整地图(全局规划) | 可局部感知(局部规划) |
| 实时性 | 中等(需搜索) | 高(实时计算受力) |
| 障碍物适配 | 静态障碍物最优 | 动态障碍物适配性好 |
| 实现复杂度 | 中等(需管理开放 / 关闭列表) | 简单(仅计算受力) |
七、结束语
- 核心原理:A * 通过评估函数f(n)=g(n)+h(n)优先搜索最优路径,启发函数h(n)是关键(需可采纳以保证最优);
- 关键步骤:初始化→循环搜索(取最小f节点→生成邻居→更新代价)→路径回溯;
- 使用要点:
- 启发函数优先选欧几里得 / 曼哈顿距离(保证可采纳);
- 步长(step_size)越小,路径越精准,但搜索效率越低;
- 适用于已知静态环境的全局最优路径规划;
- 核心优势:相比 APF,A * 不会陷入局部最小值,能保证找到最优路径。