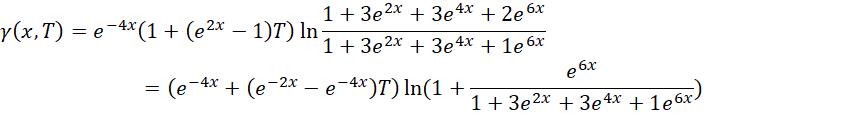
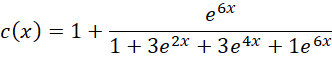
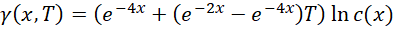
重新定义关于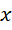
的函数，
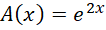
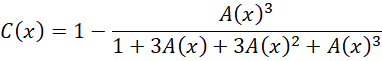
代换得到，
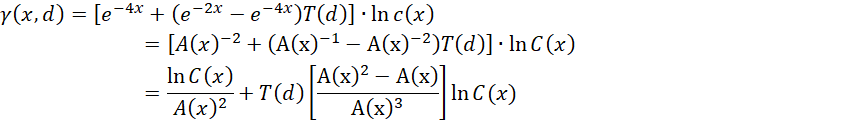
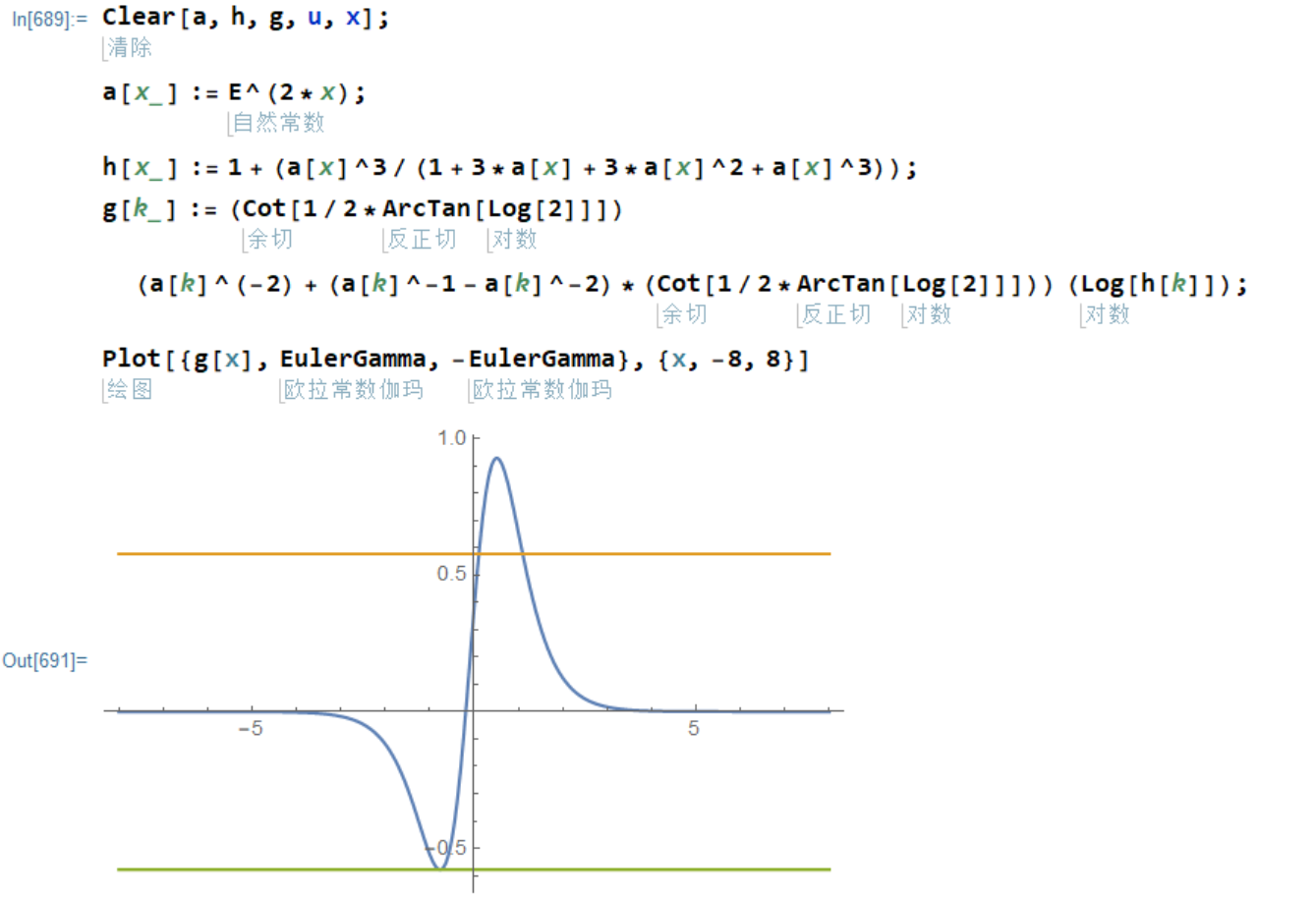
观察这个函数颠倒的图像，
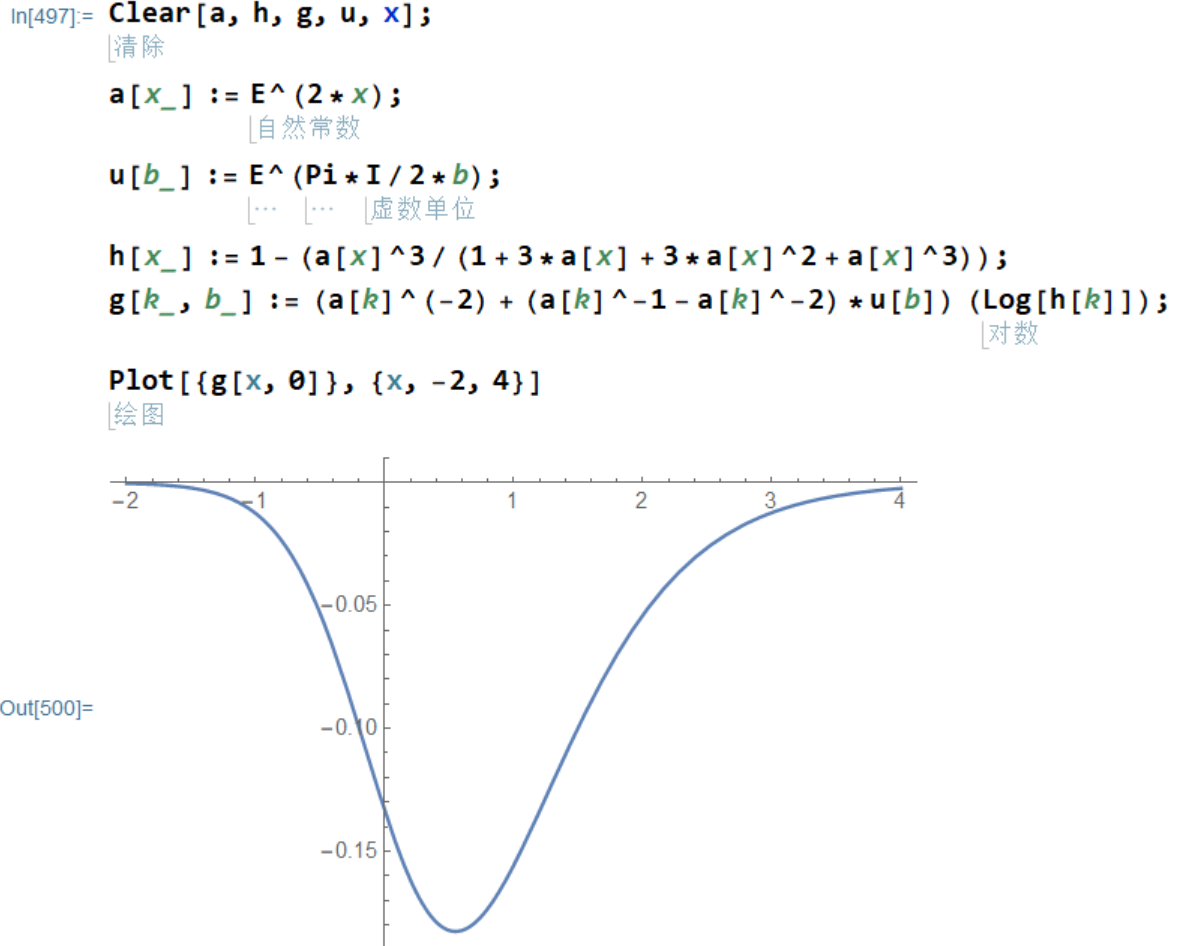
图像基本上是对称的，但也是倾斜的。
因为当前求出的极值对应的对称轴是倾斜的，所以只能旋转整个函数的图像，而且在旋转之前不知道旋转中心在哪里，所以只能基于原点做全局旋转。观察方程，
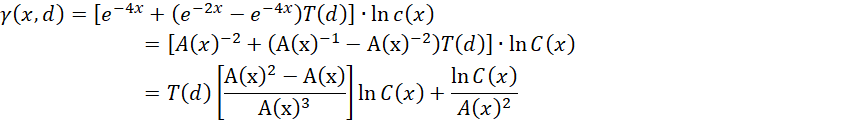
它在最宏观的层面上，具有，
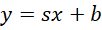
的形式，因为具体大小未知，所以暂时不考虑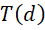
，曲线的斜率为，
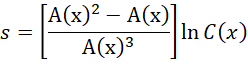
观察向着正无穷方向的斜率，
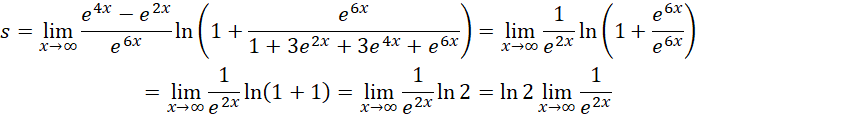
向着负无穷方向的斜率为，
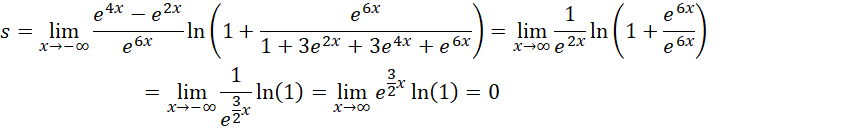
其中，
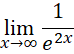
使得曲线被拉平，所以不是宏观上的斜率，宏观上的斜率为，
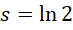
这个斜率对应的角度为，
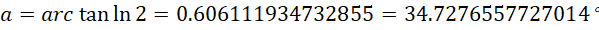
大约34°。由于负向的斜率为0，正负无穷两端造成的角度增量是一样的。因为函数图像是一个中心对称图形，所以角度要减小一半，
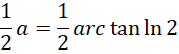
对应的正切值为，
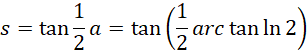
为了平衡这个斜率，需要这个正切值的倒数。这是因为这个系数是对数函数的系数，相当于对数函数自变量的指数，这个自变量的指数为1，则可以保持这个自变量本身不变，以及其对数不变，也就是使得函数值始终保持一致，函数上各点斜率为0。
在一个周期里面，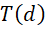
作为这个数值的倒数，就可以用于实现斜率趋向于0的平衡，
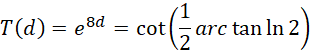
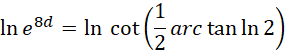
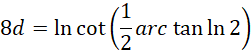
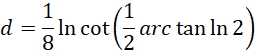
虚数单位平方之间的比率，也就是它和自身的比率为，
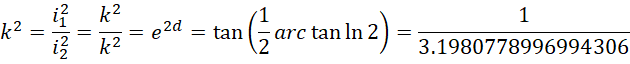
意思是，整数系统的虚数单位的平方的大小约为实数系统的虚数单位平方的大小的
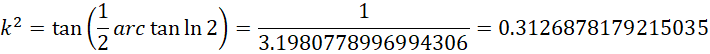
整数系统的虚数单位的大小约为实数系统的虚数单位的大小的。
整数系统的单位1的大小约为实数系统的单位1的大小的。
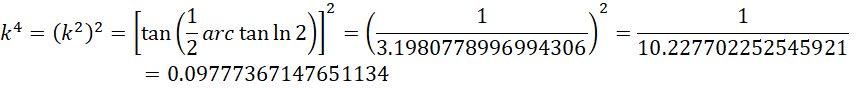
也就是说，整数系统的单位1不足实数系统单位1的十分之一。
由此，原函数化为，
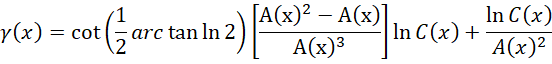
修正之后的图像为，
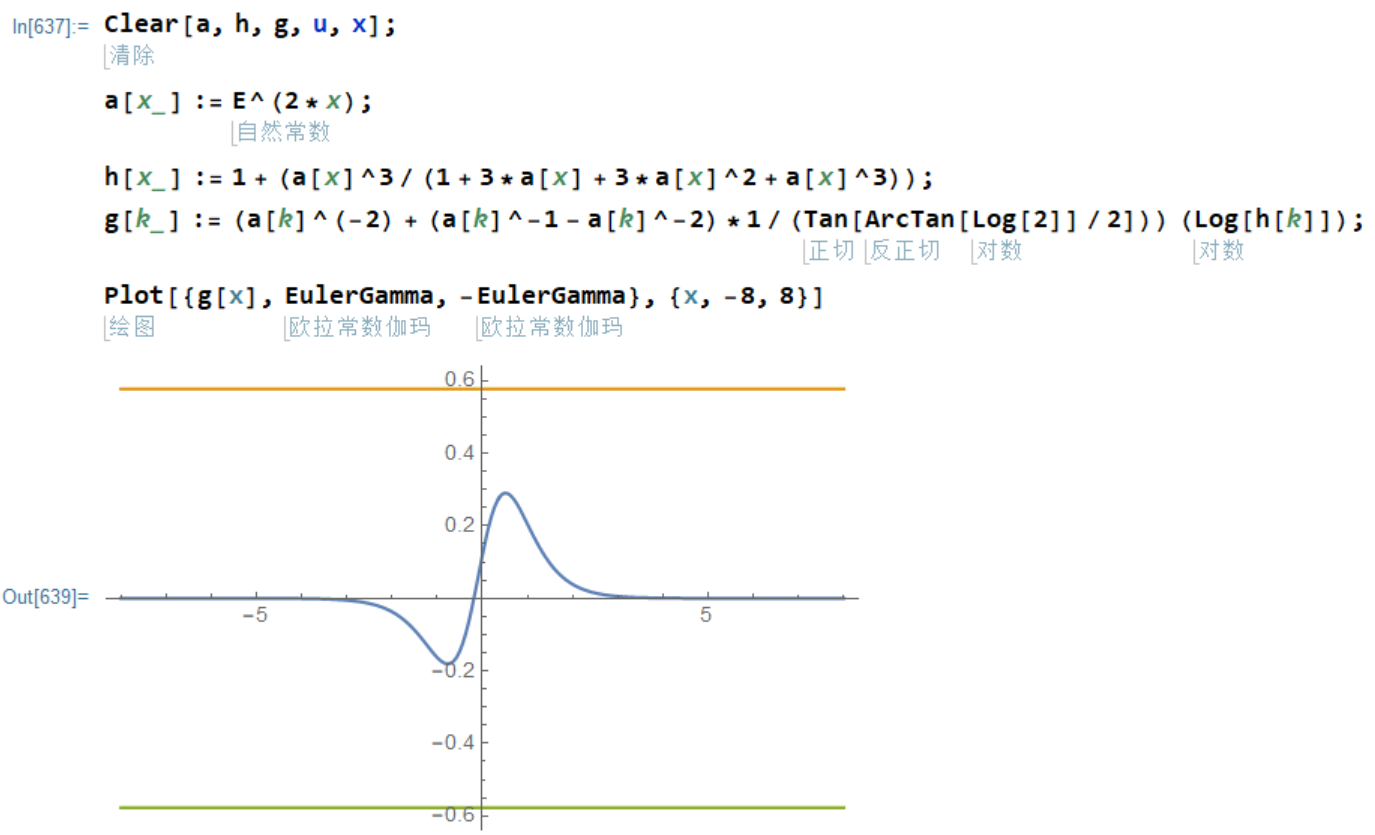
仔细考虑，我们用的积分方法，来自于二重求和，自然数倒数的无限项和，正如自然数的无限项和，应为一个负数（虚数单位的平方），所以这个结果，应开看曲线的最小值，这个值约为，
但是这个值的绝对值却小于欧拉常数的绝对值。考虑各种可能的原因，最有可能的原因就是整数系统的单位和实数系统的单位的比率不为1，而这个比率我们已经算出来了，它就是用于补偿斜率的，
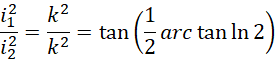
它的倒数，
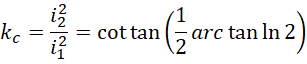
所以原函数整体上乘以这个比率的倒数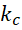
，
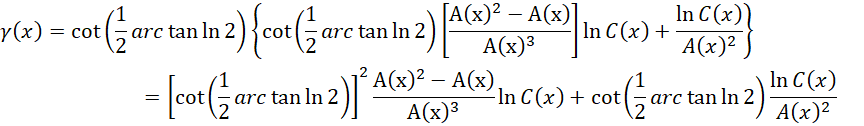
抽出常数，
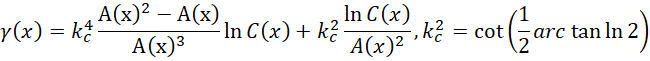
然后再求0点附近的最小值，就是欧拉伽马常数的数值的相反数，
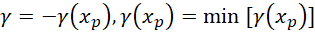
也就是方程，
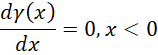
的时候函数值的相反数，
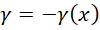
具体情况如图所示，
