回到整数单位，能够符合作为单位并保证，
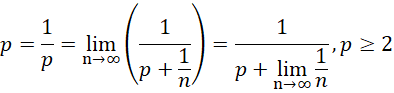
实际上只有质数，这里的范围修改为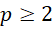
，是因为对于1来说这种形式会导致发散。
这里的函数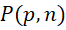
就是用
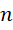决定精度的质数
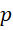的实数形式，且，
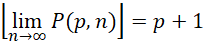
而黎曼泽塔函数，
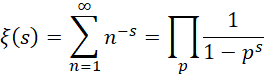
在存在无限观察者的前提下，这些质数作为单位，就符合，
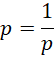
于是可以得到，
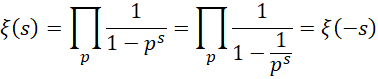
具体对于
来说，就是，
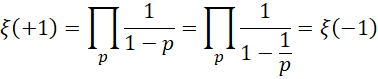
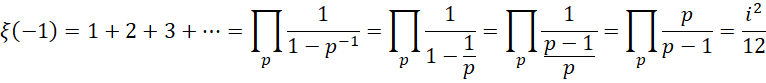
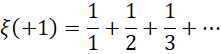
两者相加，就是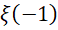
数量的两倍，
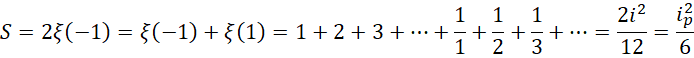
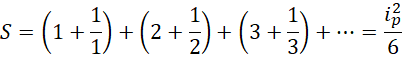
如果把每个自然数当作单位，尤其是虚数单位来理解，
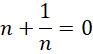
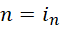
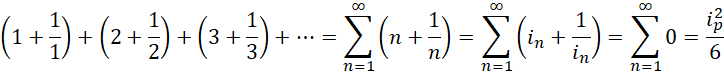
将这些虚数单位表达的半周期提升到完整周期（周期0的变换），
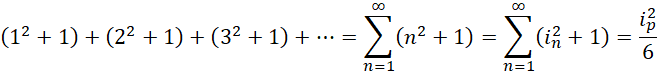
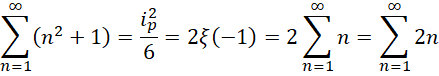
这个假设可以用如下方式验证，
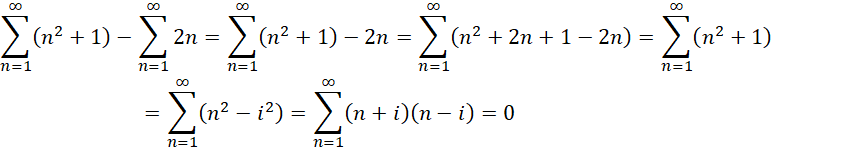
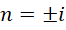
也就是说，此时每个自然数都是一个虚数单位。回到，
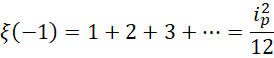
由于这个数完全是由整数累加而成，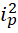
也必为整数，
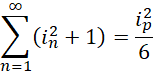
要求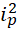
为6的倍数，由于奇质数的数量有偶数个，所以，
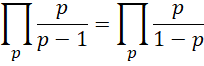
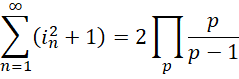
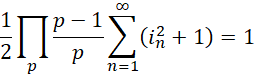
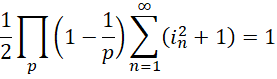
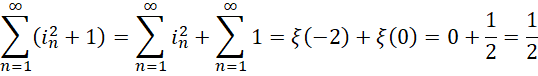
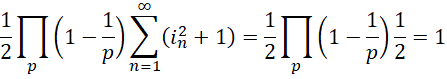
解出，
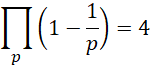
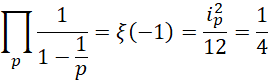
解出，
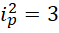
于是，
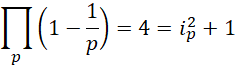
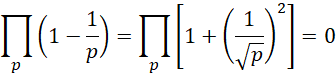
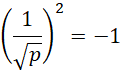
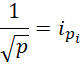
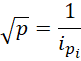
所以，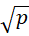
也就是每一个质数的平方根都应当被认为是虚数单位的相反数。
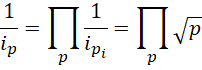
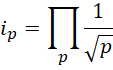
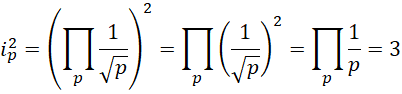
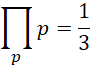
所有质数的乘积等于1/3。
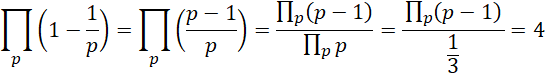
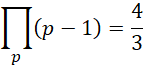
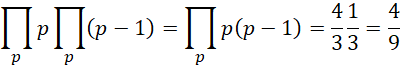
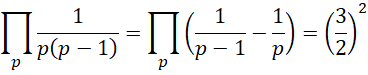
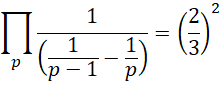
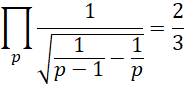
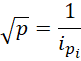
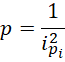
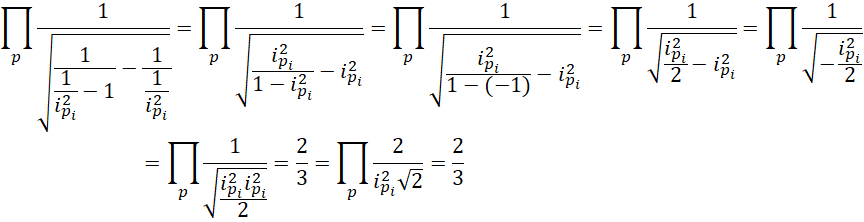
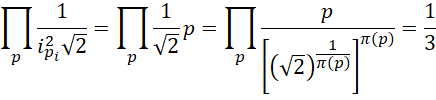
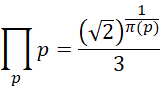
其中，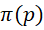
为小于或者等于质数
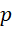的质数的个数。
先前计算得到，
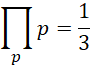
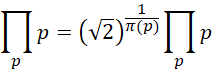
由此得到迭代方程，
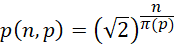
这相当于，在全乘积的过程中，如果每个新加入的数值都相等，那么这个数值就是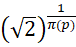
。
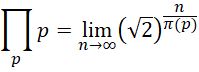
代回，
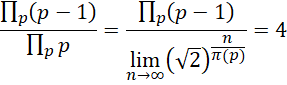
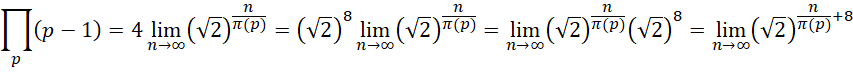
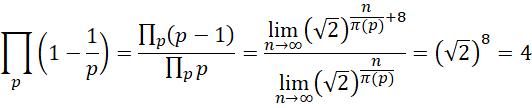
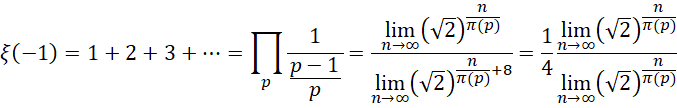
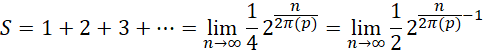
这才是自然数全加和的自然增长方式，它和有限项和，
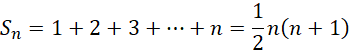
具有类似的形式，只是其中平方项被换成了2的指数形式，
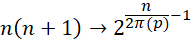
而反观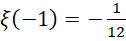
之所以能得到分数，却是是因为相对于某个基准的比例缩放结果，而这个比例涉及到虚数单位的大小数值增长的方式。
从总的虚数单位就是每个质数平方根的乘积这一点可以认识到，总的虚数单位的平方也就是"-1"也是所有质数的乘积的结果，
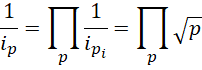
也就是说，
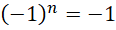
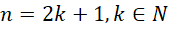
所以质数的个数虽然是无限多的，但是质数的总数是奇数，这是确定的。除了2这个偶数之外，还有偶数多个奇质数。偶数多个奇质数任选两两配对，就可以构成各种其它偶数，这符符合充分大的偶数总可以写成两个质数之和的要求。
虽然每一个质数的大小和位置并不清楚，但是所有质数的乘积是确定的1/3，而这个1/3就像-1/12一样，代表的也是某种基础上的相对量。巨大且不断变化的数值，若能得到确定不变的结果，必定是和一个相关的巨大且不断变化的数值之间构成稳定的相对关系。对于质数来说，这个结果表达为，
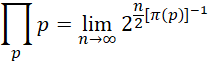
其中，
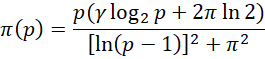
其迭代形式为，
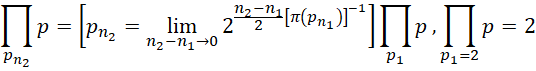
从，
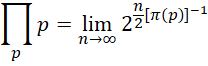
可以看出，质数都分布在，
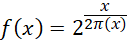
这条曲线上，其中指数中的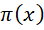
会随着x的增大而增大，它和x自身增大的速率比就决定了以2为底的指数增长的快慢。由于x的增长速率确定，就只剩下
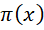的增长速率的变化造成的影响。