【算法竞赛】堆和 priority_queue

散峰而望2026-02-21 15:33
🔭 个人主页： 散峰而望

《C语言：从基础到进阶》《编程工具的下载和使用》《C语言刷题》《算法竞赛从入门到获奖》《人工智能》《AI Agent》
愿为出海月，不做归山云

🎬博主简介

【算法竞赛】堆和 priority_queue

  • 前言
  • [1. 堆的定义](#1. 堆的定义)
  • [2. 堆的存储](#2. 堆的存储)
  • [3. 核心操作](#3. 核心操作)
    • [3.1 向上调整法](#3.1 向上调整法)
    • [3.2 向下调整法](#3.2 向下调整法)
  • [4. 堆的模拟实现](#4. 堆的模拟实现)
    • [4.1 创建](#4.1 创建)
    • [4.2 插入](#4.2 插入)
    • [4.3 删除堆顶元素](#4.3 删除堆顶元素)
    • [4.4 堆顶元素](#4.4 堆顶元素)
    • [4.5 堆的大小](#4.5 堆的大小)
    • [4.6 所有测试代码](#4.6 所有测试代码)
  • [5. priority_queue](#5. priority_queue)
    • [5.1 优先级队列](#5.1 优先级队列)
    • [5.2 创建 priority_queue - 初阶](#5.2 创建 priority_queue - 初阶)
    • [5.3 size / empty](#5.3 size / empty)
    • [5.4 push](#5.4 push)
    • [5.5 pop](#5.5 pop)
    • [5.6 top](#5.6 top)
    • [5.7 初阶测试代码](#5.7 初阶测试代码)
    • [5.8 创建 priority_queue - 进阶](#5.8 创建 priority_queue - 进阶)
      • [5.8.1 内置类型](#5.8.1 内置类型)
      • [5.8.2 结构体类型](#5.8.2 结构体类型)
  • 结语

前言

堆（Heap）是一种高效的数据结构，广泛应用于算法竞赛和实际开发中，尤其在需要动态维护极值或优先级处理的场景下表现突出。其核心特性在于能够以对数时间复杂度完成插入、删除极值等操作，为贪心算法、最短路径算法（如 Dijkstra）等提供了关键支持。

优先级队列（priority_queue）是 C++ STL 对堆的封装实现，通过模板类和比较器灵活适配不同需求。理解其底层原理与使用方法，不仅能提升手动实现堆的能力，还能高效利用标准库工具解决复杂问题。

本文将从堆的存储与核心操作（如向上/向下调整）切入，逐步实现堆的完整功能，并深入解析 priority_queue 的初阶与进阶用法，包括自定义结构体的优先级规则。代码示例与测试案例贯穿全文，帮助理论与实践结合。

1. 堆的定义

堆（heap），是一棵有着特殊性质的完全二叉树，可以用来实现优先级队列（priority queue）。

堆需要满足以下性质：

  1. 是一棵完全二叉树；
  2. 对于树中每个结点，如果存在子树，那么该结点的权值大于等于（或小于等于）子树中所有结点的权值。

如果根结点大于等于子树结点的权值，称为大根堆；反之，称为小根堆。

  • 小顶堆（min heap）：任意节点的值 <= 其子节点的值。
  • 大顶堆（max heap）：任意节点的值 >= 其子节点的值。

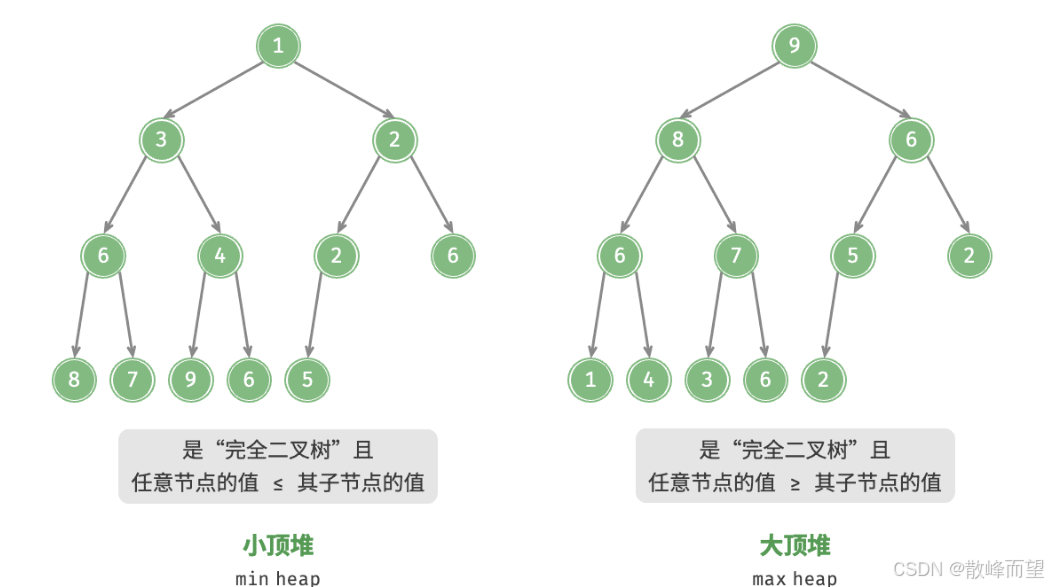
堆作为完全二叉树的一个特例，具有以下特性。

  • 最底层节点靠左填充，其他层的节点都被填满。
  • 我们将二叉树的根节点称为"堆顶"，将底层最靠右的节点称为"堆底"。
  • 对于大顶堆（小顶堆），堆顶元素（根节点）的值是最大（最小）的。

判断： 以下哪些是堆

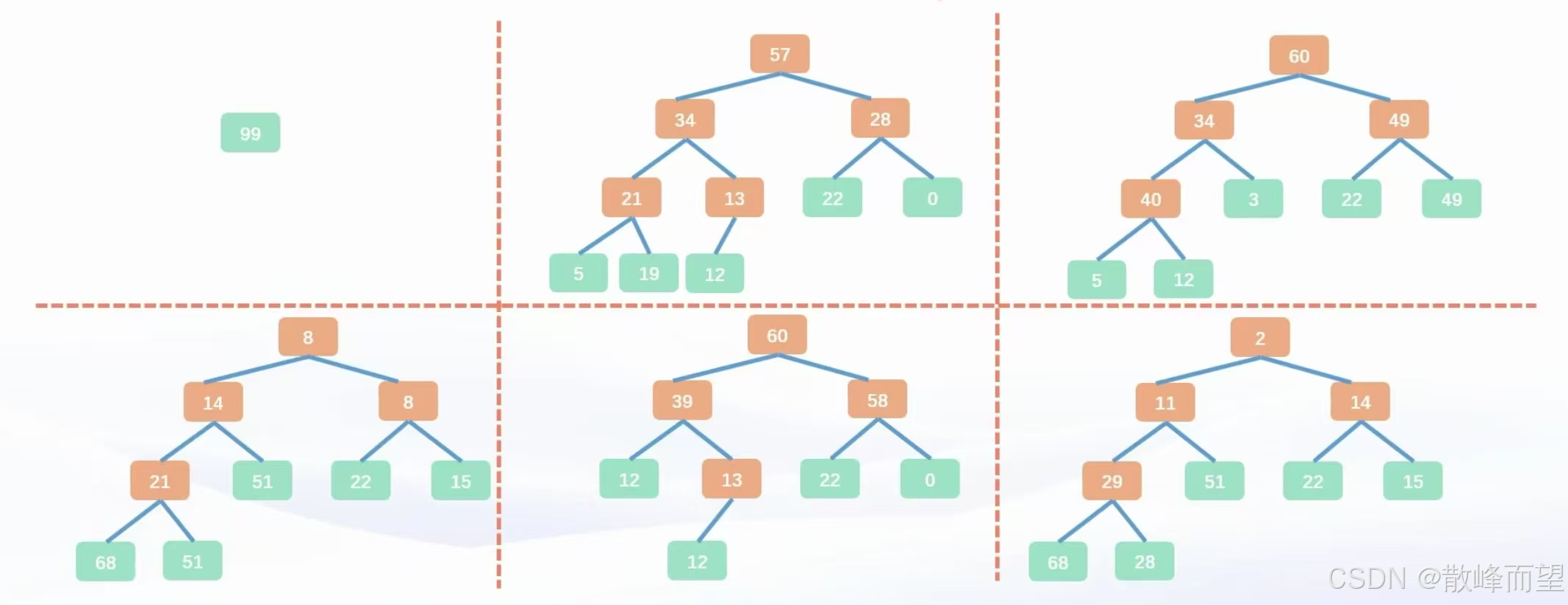
  1. 是堆，且可以是大根堆也是小根堆
  2. 是堆，是大根堆
  3. 不是堆
  4. 是堆，是小根堆
  5. 不是完全二叉树，不是堆
  6. 是堆

2. 堆的存储

由于堆是一个完全二叉树，因此可以用一个数组来存储。（如果不清楚的，可以回顾 【算法竞赛】二叉树 中的顺序存储部分）

结点下标为 i ：

  • 如果父存在，父下标为 i / 2 ；
  • 如果左孩子存在，左孩子下标为 i * 2；
  • 如果右孩子存在，右孩子下标为 i×2+1 。

题目一般给我们的是一组数，这组数按照给出的顺序还原成二叉树之后，并不是一个堆结构。此时如果想将这组数变成堆的话，有两种操作：

  1. 用数组存下来这组数，然后把数组调整成一个堆；
  2. 创建一个堆，然后将这组数依次插入到堆中。

3. 核心操作

堆中的所有运算，比如建堆，向堆中插入元素以及删除元素等，都是基于堆中的两个核心操作实现的 --- 向上调整算法以及向下调整算法。

因此，在实现堆之前，先来掌握两种核心操作。

以下所有操作都默认堆是一个大根堆，小根堆的原理反着来即可。

3.1 向上调整法

用于向堆中插入元素，就是当堆中新来一个元素。放在队尾时，从这个节点开始，逐渐向上调整。

算法流程：

  1. 与父结点的权值作比较，如果比它大，就与父亲交换；
  2. 交换完之后，重复 1. 操作，直到比父亲小，或者换到根节点的位置。

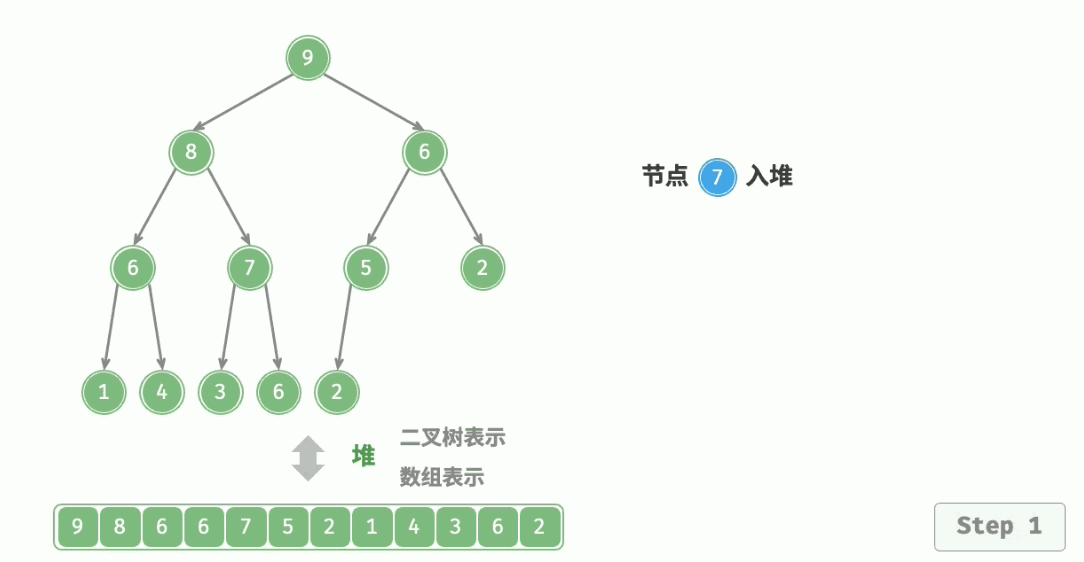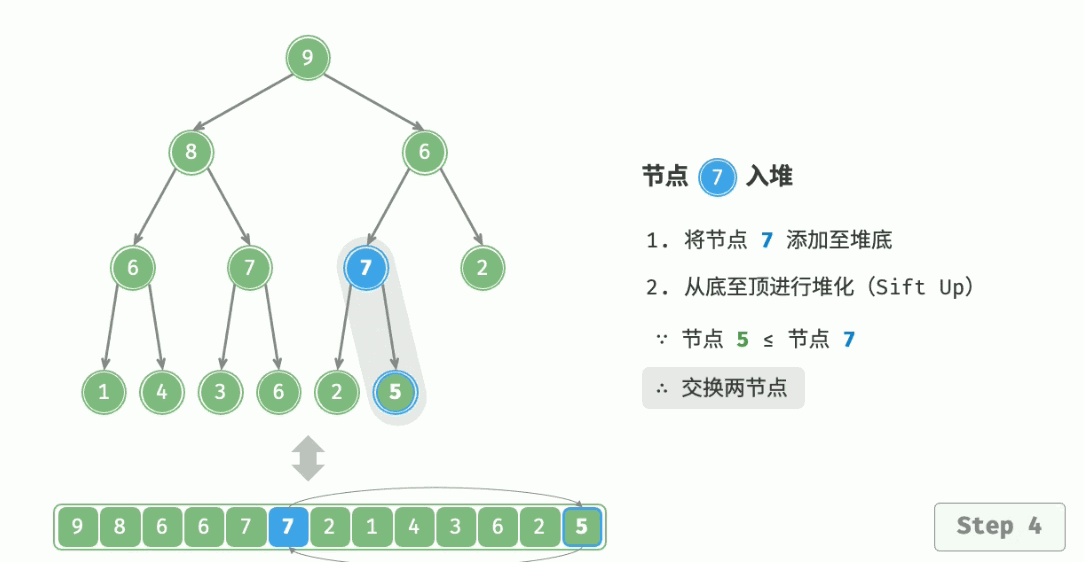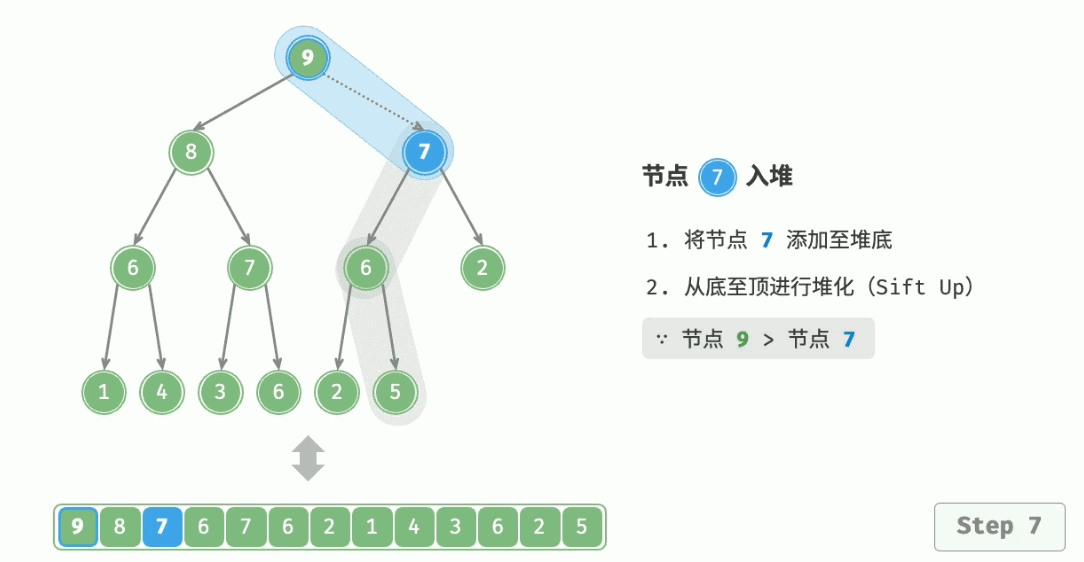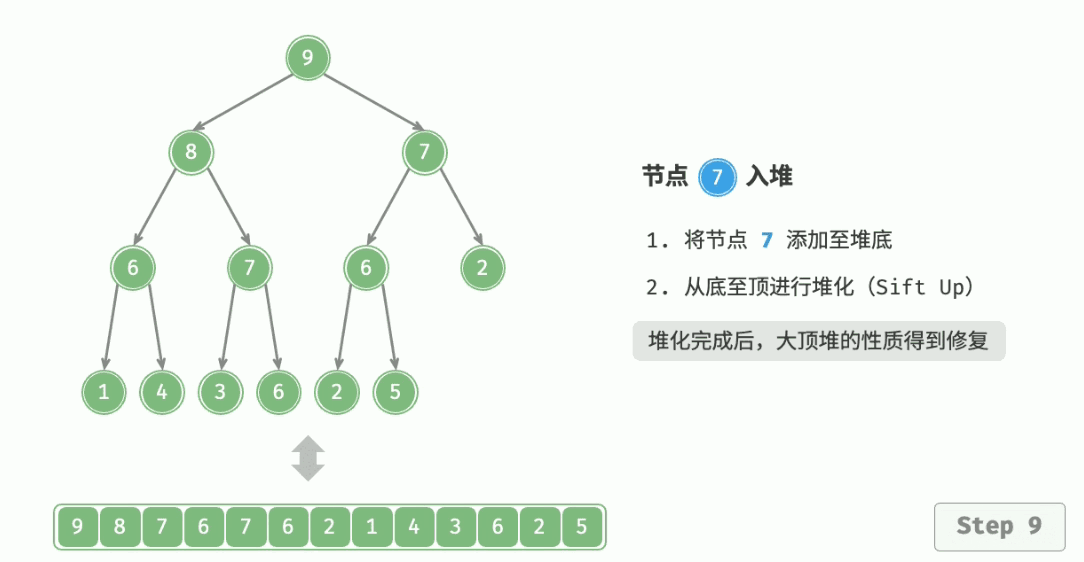
代码实现：

cpp 复制代码 
//向上调整
void up(int child)
{
	int parent = child / 2;
	
	//父亲节点存在，并且大于父节点的权值
	while(parent >= 1 && heap[child] > heap[parent])
	{
		swap(heap[child], heap[parent]);
		//交换后，修改下次调整的父子关系
		child = parent;
		parent = child / 2;
	 } 
 }

小根堆的调整只需要改成 heap[child] < heap[parent]

时间复杂度：

最差情况需要走一个树高，因此时间复杂度为 O(logN)

3.2 向下调整法

用于删除堆顶元素，或者堆排序中的建堆操作。从这个节点开始逐渐向下调整。

算法流程：

  1. 找出左右儿子中权值最大的那个，如果比它小，就与其交换；
  2. 交换完之后，重复 1. 操作，直到比儿子结点的权值都大，或者换到叶节点的位置。

代码实现：

cpp 复制代码 
//向下调整
void down(int parent)
{
	int child = parent * 2;//左孩子
	
	while(child <= n)//如果还有孩子，因为是完全二叉树，所以没有左孩子一定没有右孩子
	{
		//找出两个孩子哪个最大
		if(child + 1 <= n && heap[child + 1] > heap[heap]) child++;
		//最大孩子都比我小，说明是合法堆
		if(heap[child] < heap[parent]) return;
		
		swap(heap[child], heap[parent]);
		//交换后，修改下次调整的父子关系
		parent = child;
		child = parent * 2; 
	 } 
 }

小根堆只需要把判断大的改成小的即可 heap[parent] < heap[child]

时间复杂度：

最差情况需要走一个树高，因此时间复杂度为 O(logN)

4. 堆的模拟实现

4.1 创建

"二叉树"章节讲过，完全二叉树非常适合用数组来表示。由于堆正是一种完全二叉树，因此我们将采用数组来存储堆。

  • 创建一个足够大的数组充当堆；
  • 创建一个变量 n，用来标记堆中元素的个数。
cpp 复制代码 
const int N = 1e6 + 10;

int n;//标记堆的大小，即有多少元素
int heap[N];//存堆-大根堆

4.2 插入

把新来的元素放在最后一个位置，然后从最后一个位置开始执行一次向上调整算法即可。

cpp 复制代码 
//向上调整
void up(int child)
{
	int parent = child / 2;
	
	//父亲节点存在，并且大于父节点的权值
	while(parent >= 1 && heap[child] > heap[parent])
	{
		swap(heap[child], heap[parent]);
		//交换后，修改下次调整的父子关系
		child = parent;
		parent = child / 2;
	 } 
 } 
 
//插入
void push(int x)
{
	heap[++n] = x;
	
	up(n);
 }

时间复杂度：

时间开销在向上调整算法上，时间复杂度为 O(logN)

4.3 删除堆顶元素

  1. 将栈顶元素和最后一个元素交换，然后 n--，删除最后一个元素；
  2. 从根节点开始执行一次向下调整算法即可。


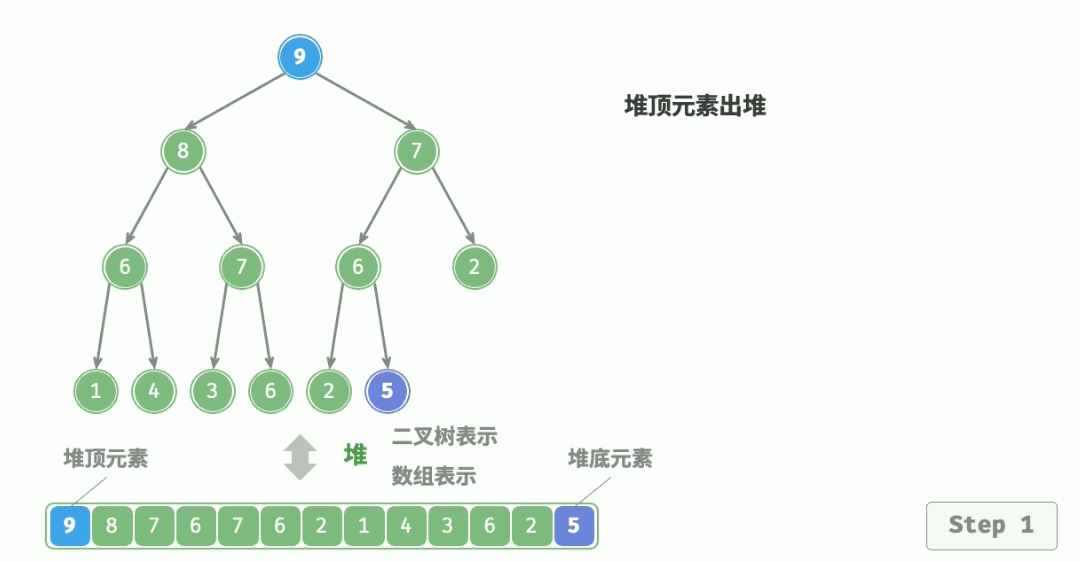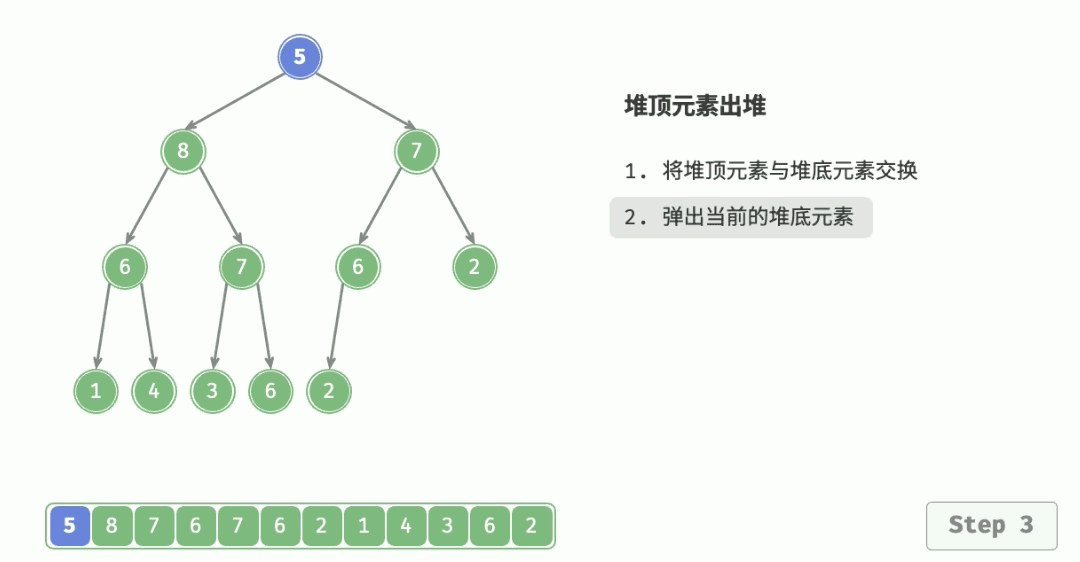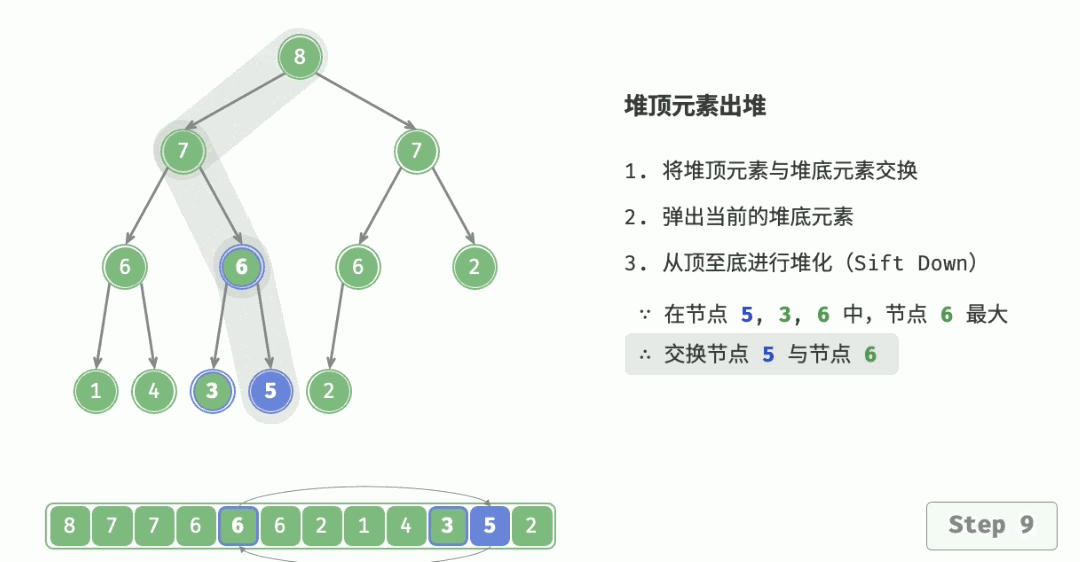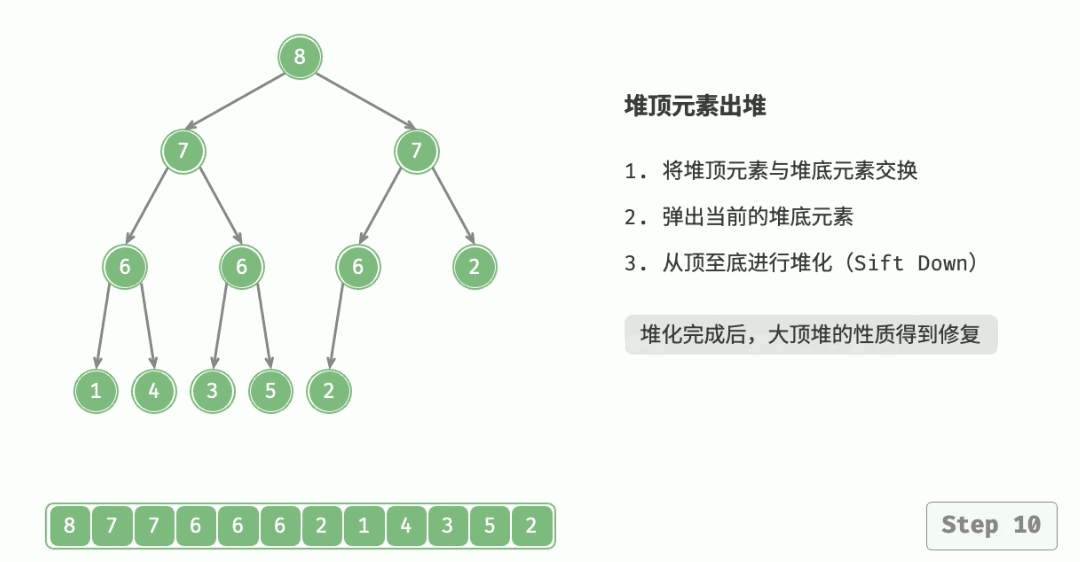
代码实现：

cpp 复制代码 
//向下调整
void down(int parent)
{
	int child = parent * 2;//左孩子
	
	while(child <= n)//如果还有孩子，因为是完全二叉树，所以没有左孩子一定没有右孩子
	{
		//找出两个孩子哪个最大
		if(child + 1 <= n && heap[child + 1] > heap[parent]) child++;
		//最大孩子都比我小，说明是合法堆
		if(heap[child] < heap[parent]) return;
		
		swap(heap[child], heap[parent]);
		//交换后，修改下次调整的父子关系
		parent = child;
		child = parent * 2; 
	 } 
 } 

//删除堆顶元素
void pop()
{
	//把第一个元素与最后一个元素交换
	swap(heap[1], heap[n]);
	n--;
	 
	down(1); 
 }

时间复杂度：

时间开销在向下调整算法上，时间复杂度为 O(logN)

4.4 堆顶元素

下标为 1 位置的元素，就是堆顶元素。

代码实现：

cpp 复制代码 
// 堆顶元素 
int top()
{
    return heap[1];
}

时间复杂度：

O(1)

4.5 堆的大小

n 的值。

cpp 复制代码 
// 堆的大小 
int size()
{
    return n;
}

时间复杂度：

O(1)

4.6 所有测试代码

cpp 复制代码 
//堆
#include <iostream>

using namespace std;

const int N = 1e6 + 10;

int n;//标记堆的大小，即有多少元素
int heap[N];//存堆-大根堆 

//向上调整
void up(int child)
{
	int parent = child / 2;
	
	//父亲节点存在，并且大于父节点的权值
	while(parent >= 1 && heap[child] > heap[parent])
	{
		swap(heap[child], heap[parent]);
		//交换后，修改下次调整的父子关系
		child = parent;
		parent = child / 2;
	 } 
 } 
 
//插入
void push(int x)
{
	heap[++n] = x;
	
	up(n);
 }  

//向下调整
void down(int parent)
{
	int child = parent * 2;//左孩子
	
	while(child <= n)//如果还有孩子，因为是完全二叉树，所以没有左孩子一定没有右孩子
	{
		//找出两个孩子哪个最大
		if(child + 1 <= n && heap[child + 1] > heap[parent]) child++;
		//最大孩子都比我小，说明是合法堆
		if(heap[child] < heap[parent]) return;
		
		swap(heap[child], heap[parent]);
		//交换后，修改下次调整的父子关系
		parent = child;
		child = parent * 2; 
	 } 
 } 

//删除堆顶元素
void pop()
{
	//把第一个元素与最后一个元素交换
	swap(heap[1], heap[n]);
	n--;
	 
	down(1); 
 } 

// 堆顶元素 
int top()
{
    return heap[1];
}

// 堆的大小 
int size()
{
    return n;
}

int main()
{
	//测试堆
	int a[10] = {1, 3, 42, 23, 11, 2, -1, 0, 99, 15}; 
	
	//入堆
	for(int i = 0; i < 10; i++)
	{
		push(a[i]);
	 } 
	
	while(size())
	{
		cout << top() << " ";
		pop();
	 } 
	 
	return 0; 
}

测试结果：

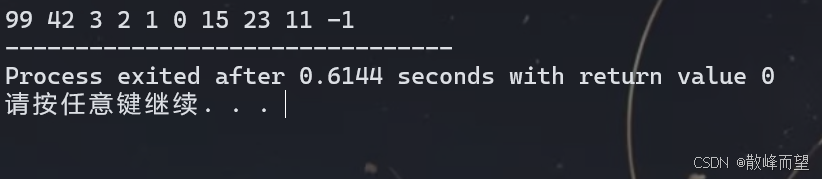
5. priority_queue

5.1 优先级队列

普通的队列是一种先进先出的数据结构，即元素插入在队尾，而元素删除在队头。

而在优先级队列 中，元素被赋予优先级，当插入元素时，同样是在队尾，但是会根据优先级进行位置调整，优先级越高，调整后的位置越靠近队头；同样的，删除元素也是根据优先级进行，优先级最高的元素（队头）最先被删除。

其实可以认为，优先级队列就是堆实现的一个数据结构。

priority_queue 就是 C++ 提供的，已经实现好的优先级队列，底层实现就是一个堆结构。在算法竞赛中，如果是需要使用堆的题目，一般就直接用现的 priority_queue，很少手写一个堆，因为省事。

5.2 创建 priority_queue - 初阶

优先级队列的创建结果有很多种，因为需要根据实际需求，可能会创建出来各种各样的堆：

  1. 简单内置类型的大根堆或小根堆：比如存储 int 类型的大根堆或小根堆；
  2. 存储字符串的大根堆或小根堆；
  3. 存储自定义类型的大根堆或小根堆：比如堆里面的数据是一个结构体。

关于每一种创建结果，都需要有与之对应的写法。在初阶阶段，先用简单的 int 类型建堆，重点学习 priority_queue 的用法。

注意：priority_queue 包含在 queue 这个头文件中。

cpp 复制代码 
#include <iostream>
#include <vector>
#include <queue> // 优先级队列的头文件在 queue 里面 
using namespace std;
// 优先级队列的使用 
void test1()
{
    int a[10] = {1, 41, 23, 10, 11, 2, -1, 99, 14, 0};
    priority_queue<int> heap; // 默认写法下，是一个大根堆 
}

5.3 size / empty

  1. size：返回元素的个数。
  2. empty：返回优先级队列是否为空。

时间复杂度：

O(1)

5.4 push

往优先级队列里面添加一个元素。

时间复杂度：

因为底层是一个堆结构，所以时间复杂度为 O(logN)

5.5 pop

删除优先级最高的元素。

时间复杂度：

因为底层是一个堆结构，所以时间复杂度为 O(logN)

5.6 top

获取优先级最高的元素。

时间复杂度：

O(1)

5.7 初阶测试代码

cpp 复制代码 
#include <iostream>
#include <vector>
#include <queue> // 优先级队列的头文件在 queue 里面 
using namespace std;
// 优先级队列的使用 

int a[10] = {1, 41, 23, 10, 11, 2, -1, 99, 14, 0};
    
int main()
{
	priority_queue<int> heap; // 默认写法下，是一个大根堆
	
	for(int i = 0; i < 10; i++)
	{
		heap.push(a[i]);
	 } 
	
	while(heap.size())
	{
		cout << heap.top() << " ";
		heap.pop();
	 } 
	
	return 0; 
}

测试结果：

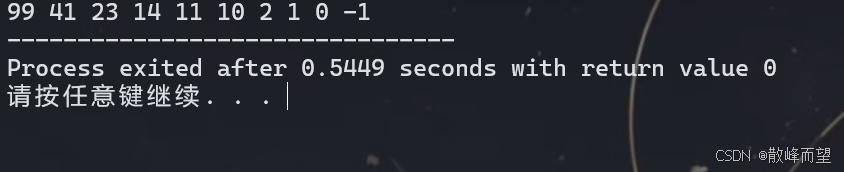
5.8 创建 priority_queue - 进阶

5.8.1 内置类型

内置类型就是 C++ 提供的数据类型，比如 int、double、long long 等。以 int 类型为例，分别创建大根堆和小根堆。

priority_queue<数据类型， 存数据的结构， 数据之间的比较方式>

cpp 复制代码 
#include <iostream>
#include <vector>
#include <queue>

using namespace std;

int a[10] = {1, 41, 23, 10, 11, 2, -1, 99, 14, 0};

//内置类型
void test()
{
	// 大根堆 
    priority_queue<int> heap1; // 默认就是大根堆 
    // priority_queue<数据类型， 存数据的结构， 数据之间的比较方式> 
    priority_queue<int, vector<int>, less<int>> heap2; // 也是大根堆 
    // 小根堆 
    priority_queue<int, vector<int>, greater<int>> heap3; // 小根堆 
    // 测试 
    for(auto x : a)
    {
        heap1.push(x);
        heap2.push(x);
        heap3.push(x);
    }
    while(heap1.size())
    {
        cout << heap1.top() << " "; // 获取堆顶元素的值 
        heap1.pop(); // 删除元素 
    }
    cout << endl;
    while(heap2.size())
    {
        cout << heap2.top() << " "; // 获取堆顶元素的值 
        heap2.pop(); // 删除元素 
    }
    cout << endl;
    while(heap3.size())
    {
        cout << heap3.top() << " "; // 获取堆顶元素的值 
        heap3.pop(); // 删除元素 
    }
    cout << endl;
}

int main()
{
    test();
    return 0;
}

测试结果：

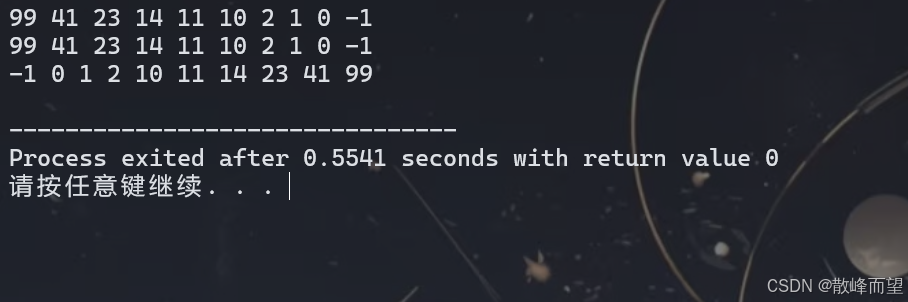
5.8.2 结构体类型

当优先级队列里面存的是结构体类型时，需要在结构体中重载 < 比较运算符，从而创建出大根堆或者小根堆。

cpp 复制代码 
#include <iostream>
#include <vector>
#include <queue>

using namespace std;
struct node
{
    int a, b, c;
     // 以 b 为基准，定义大根堆 
     bool operator < (const node& x) const
     {
         return b < x.b;
     }
//    // 以 b 为基准，定义小根堆 
//    bool operator < (const node& x) const
//    {
//        return b > x.b;
//    }
};
void test()
{
    priority_queue<node> heap;
    for(int i = 1; i <= 10; i++)
    {
        heap.push({i, i + 1, i + 2});
    }
    while(heap.size())
    {
        node t = heap.top();
        heap.pop();
        cout << t.a << " " << t.b << " " << t.c << endl;
    }
}
int main()
{
    test();
    return 0;
}

结语

堆作为一种高效维护动态极值的数据结构，在算法竞赛中广泛应用于排序、贪心、最短路径等场景。其核心操作（上浮与下沉）通过对数级时间复杂度保证了性能优势，而数组存储方式进一步提升了空间利用率。

优先队列（priority_queue）作为堆的标准库实现，封装了底层细节并支持自定义优先级，极大简化了开发流程。无论是处理内置类型还是结构体，通过重载比较函数或仿函数均可灵活调整排序规则。

掌握手动模拟堆的实现有助于深入理解其原理，而熟练使用 STL 的优先队列则能显著提升编码效率。两者结合，将为解决复杂算法问题提供强有力的工具支撑。

愿诸君能一起共渡重重浪，终见缛彩遥分地，繁光远缀天。

相关推荐
adore.9681 小时前
2.20 oj83+84+85
c++·复试上机
WarPigs1 小时前
UI显示任务目的地标记的方法
算法·ui
蚊子码农2 小时前
算法题解记录-560和为k的子数组
算法
alexwang2112 小时前
B2007 A + B 问题 题解
c++·算法·题解·洛谷
重生之后端学习2 小时前
46. 全排列
数据结构·算法·职场和发展·深度优先·图论
wostcdk2 小时前
数论学习1
数据结构·学习·算法
javaIsGood_2 小时前
Java基础面试题
java·开发语言
我是中国人哦(⊙o⊙)2 小时前
我的寒假作业
人工智能·算法·机器学习
Zik----2 小时前
Leetcode2 —— 链表两数相加
数据结构·c++·leetcode·链表·蓝桥杯
热门推荐
01GitHub 镜像站点02AI Agent 平台横评：ZeroClaw vs OpenClaw vs Nanobot03Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services04MIUI显示/隐藏5G开关的方法，信号弱时开启手机Wifi通话方法05从零搭建一个 PHP 登录注册系统（含完整源码）06如何解决 OpenClaw “Pairing required” 报错：两种官方解决方案详解07全面体验 Grok API 中转站（2025 · Grok 4 系列最新版）08配置 OpenClaw 使用 Ollama 本地模型09openClaw安装飞书插件｜核心踩坑：spawn EINVAL 错误终极解决指南10使用 1panel面板 部署 php网站