**FA:**formulas and algorithm,LSLAM:lidar simultaneous localization and mapping,**NDT:**normal distributions transform
一、NDT 匹配核心原理(从本质到定义)
1. 核心定义
正态分布变换(Normal Distributions Transform,NDT) 是由 Biber 和 Strasser 在 2003 年提出的基于概率密度估计的点云配准算法,核心思想:
- 将参考点云(目标点云)的空间划分为规则的网格(体素);
- 对每个网格内的点计算多维正态分布(均值、协方差矩阵),构建概率密度模型;
- 将待配准点云(源点云)的每个点投影到该概率模型中,通过优化目标函数找到最优的位姿变换(旋转 + 平移),使源点云在参考点云的概率模型中 "概率最大化"。
2. 核心优势
- 无需点云特征提取(如 ICP 需要对应点),配准效率更高;
- 对初始位姿要求低于 ICP(但仍需一定初始值);
- 适合大规模点云配准,计算复杂度低。
二、NDT 数学公式推导(从概率模型到优化目标)
1. 第一步:体素划分与正态分布估计
将参考点云P=p1,p2,...,pnP={p_1,p_2,...,p_n}P=p1,p2,...,pn的空间划分为大小为d×d×d(2D 为d×d)的体素网格:
-
对于每个非空体素VkV_kVk,包含点集Pk=pi∈P∣pi∈VkP_k={p_i∈P∣p_i∈V_k}Pk=pi∈P∣pi∈Vk;
-
计算体素VkV_kVk内点的均值 μkμ_kμk:
μk=1m∑p∈Pkpμ_k=\frac{1}{m}\sum_{p∈P_k}pμk=m1∑p∈Pkp其中m是体素内点的数量;
-
计算体素VkV_kVk内点的协方差矩阵 ΣkΣ_kΣk:
∑k=1m−1∑p∈Pk(p−μk)(p−μk)T\sum_k=\frac{1}{m-1}\sum_{p∈P_k}(p−μ_k)(p−μ_k)^T∑k=m−11∑p∈Pk(p−μk)(p−μk)T
2. 第二步:概率密度函数(PDF)
每个体素VkV_kVk内的点服从多维正态分布,其概率密度函数为:
p(x)=1(2π)D∣∑k∣p(x)=\frac{1}{\sqrt{(2π)^D|\sum_k|}}p(x)=(2π)D∣∑k∣ 1exp−12((x−μk)T)∑k−1(x−uk)-\frac{1}{2}((x−μ_k)^T)\sum_{k}^{-1}(x-u_k)−21((x−μk)T)∑k−1(x−uk)
其中:
- D是点云维度(2D 为 2,3D 为 3);
- ∣Σk∣∣Σ_k∣∣Σk∣是协方差矩阵的行列式;
- Σk−1Σ_{k}^{−1}Σk−1是协方差矩阵的逆矩阵。
3. 第三步:目标函数构建
NDT 的核心是找到最优位姿变换T(ξ)T(ξ)T(ξ)(ξ为变换参数,如 2D 下ξ=[tx,ty,θ]),使得源点云Q=q1,q2,...,qmQ={q_1,q_2,...,q_m}Q=q1,q2,...,qm经过变换后的点T(ξ)qiT(ξ)q_iT(ξ)qi在参考点云的 NDT 模型中概率密度之和最大化。
为了方便优化(将最大化转为最小化),定义负对数似然函数 作为目标函数:
f(ξ)=−∑q∈Q[−12(T(ξ)q−μk)TΣk−1(T(ξ)q−μk)−D2ln(2π)−12ln∣Σk∣]f(ξ)=−\sum_{q∈Q}[−\frac{1}{2}(T(ξ)q−μ_k)^TΣ_{k}^{−1}(T(ξ)q−μ_k)−\frac{D}{2}ln(2π)−\frac{1}{2}ln∣Σ_k∣]f(ξ)=−∑q∈Q[−21(T(ξ)q−μk)TΣk−1(T(ξ)q−μk)−2Dln(2π)−21ln∣Σk∣]
忽略常数项(D2ln(2π)\frac{D}{2}ln(2π)2Dln(2π)、12ln∣∑k∣\frac{1}{2}ln|\sum_k|21ln∣∑k∣),简化为:
f(ξ)=12∑q∈Q(T(ξ)q−μk)T∑k−1(T(ξ)q−μk)f(ξ)=\frac{1}{2}\sum_{q∈Q}(T(ξ)q−μ_k)^T\sum_k^{−1}(T(ξ)q−μ_k)f(ξ)=21∑q∈Q(T(ξ)q−μk)T∑k−1(T(ξ)q−μk)
我们的目标是找到ξ∗使得f(ξ∗)最小:ξ∗=argminξf(ξ)ξ∗=arg min_ξf(ξ)ξ∗=argminξf(ξ)
4. 第四步:位姿变换与梯度下降优化
-
2D 位姿变换 :变换参数ξ=[tx,ty,θ]ξ=[t_x,t_y,θ]ξ=[tx,ty,θ],点q=(x,y)q=(x,y)q=(x,y)的变换为:
T(ξ)q=[cosθ−sinθsinθcosθ][xy]+[txty]T(ξ)q=\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}\begin{bmatrix}x \\ y \end{bmatrix}+\begin{bmatrix}t_x\\t_y\end{bmatrix}T(ξ)q=[cosθsinθ−sinθcosθ][xy]+[txty]
-
优化方法 :使用牛顿 - 拉夫逊法或高斯 - 牛顿法 求解最优ξ,核心是计算目标函数的梯度∇f(ξ)∇f(ξ)∇f(ξ)和海森矩阵H(ξ)H(ξ)H(ξ),迭代更新:
ξk+1=ξk−H(ξk)−1∇f(ξk)ξ_{k+1}=ξ_k−H(ξ_k)^{−1}∇f(ξ_k)ξk+1=ξk−H(ξk)−1∇f(ξk)
三、NDT 匹配操作步骤(工程落地版)
步骤 1:预处理
- 加载参考点云P和源点云Q;
- 对源点云 / 参考点云进行下采样(降低点数量,提高效率);
- 初始化位姿变换ξ0(如 2D 下ξ0=[0,0,0],即无初始变换)。
步骤 2:构建 NDT 模型(参考点云)
- 划分体素网格:根据参考点云的空间范围,设置体素大小(如 2D 用 1m×1m);
- 对每个体素计算均值μk和协方差矩阵ΣkΣ_kΣk;
- 过滤空体素或点数量过少的体素(如少于 3 个点,协方差矩阵不可逆)。
步骤 3:迭代优化位姿
- 将源点云的每个点通过当前位姿ξkξ_kξk变换到参考点云坐标系;
- 找到每个变换后点所属的体素VkV_kVk;
- 计算目标函数f(ξk)f(ξ_k)f(ξk)、梯度∇f(ξk)∇f(ξ_k)∇f(ξk)和海森矩阵H(ξk)H(ξ_k)H(ξk);
- 更新位姿ξk+1=ξk−α⋅H(ξk)−1∇f(ξk)ξ_{k+1}=ξ_k−α⋅H(ξ_k)^{−1}∇f(ξ_k)ξk+1=ξk−α⋅H(ξk)−1∇f(ξk)(ααα为步长);
- 检查收敛条件(如位姿变化量小于阈值、目标函数变化小于阈值),若未收敛则重复步骤 1-4。
步骤 4:输出结果
- 最优位姿变换ξ∗ξ^∗ξ∗;
- 变换后的源点云(与参考点云配准)。
四、NDT 实现方法(关键细节)
| 环节 | 关键实现细节 |
|---|---|
| 体素划分 | 2D 用二维网格,3D 用三维体素;体素大小需平衡效率和精度(越大越快,越小越准) |
| 协方差计算 | 体素内点数量需≥3(2D)/4(3D),否则协方差矩阵奇异;可添加正则项避免不可逆 |
| 优化方法 | 优先用高斯 - 牛顿法(计算量小于牛顿法),需实现梯度和海森矩阵的解析推导 |
| 下采样 | 用体素下采样(VoxelGrid),降低点数量,提升配准速度 |
| 收敛条件 | 位姿变化阈值(如Δtx<1e−4)、目标函数变化阈值(如Δf<1e−6) |
五、Python 代码实现(2D NDT 匹配)
1. 前置依赖
bash
pip install numpy matplotlib scipy open3d # open3d用于点云处理2. 完整代码
bash
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize as opt
from scipy.spatial import KDTree
import open3d as o3d
class NDTMatcher2D:
"""2D正态分布变换(NDT)点云配准类"""
def __init__(self, voxel_size=1.0, step_size=0.1, tolerance=1e-4, max_iter=100):
"""
初始化NDT参数
:param voxel_size: 体素大小(m)
:param step_size: 优化步长
:param tolerance: 收敛阈值
:param max_iter: 最大迭代次数
"""
self.voxel_size = voxel_size
self.step_size = step_size
self.tolerance = tolerance
self.max_iter = max_iter
# 参考点云的NDT模型
self.voxel_means = {} # 体素均值 {voxel_key: mean}
self.voxel_covs = {} # 体素协方差 {voxel_key: cov}
self.voxel_points = {} # 体素内点 {voxel_key: points}
def _get_voxel_key(self, point):
"""获取点所属的体素键(整数坐标)"""
x = int(np.floor(point[0] / self.voxel_size))
y = int(np.floor(point[1] / self.voxel_size))
return (x, y)
def build_ndt_model(self, ref_points):
"""构建参考点云的NDT模型"""
# 1. 划分体素
for p in ref_points:
key = self._get_voxel_key(p)
if key not in self.voxel_points:
self.voxel_points[key] = []
self.voxel_points[key].append(p)
# 2. 计算每个体素的均值和协方差
for key, points in self.voxel_points.items():
points = np.array(points)
if len(points) < 3: # 至少3个点计算协方差
continue
# 计算均值
mean = np.mean(points, axis=0)
# 计算协方差矩阵
cov = np.cov(points.T)
# 添加正则项避免奇异矩阵
cov += 1e-6 * np.eye(2)
# 检查协方差矩阵是否可逆
if np.linalg.det(cov) < 1e-8:
continue
self.voxel_means[key] = mean
self.voxel_covs[key] = cov
def _transform_point(self, point, xi):
"""
2D位姿变换:xi = [tx, ty, theta]
:param point: 源点 (x,y)
:param xi: 变换参数 [tx, ty, theta]
:return: 变换后的点
"""
tx, ty, theta = xi
# 旋转矩阵
R = np.array([
[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]
])
# 变换:R*p + t
transformed = R @ point + np.array([tx, ty])
return transformed
def _ndt_cost(self, xi, src_points):
"""
NDT目标函数(负对数似然)
:param xi: 变换参数 [tx, ty, theta]
:param src_points: 源点云
:return: 目标函数值
"""
cost = 0.0
n_points = 0
for p in src_points:
# 1. 变换点
p_transformed = self._transform_point(p, xi)
# 2. 找到所属体素
key = self._get_voxel_key(p_transformed)
if key not in self.voxel_means:
continue
# 3. 获取体素的均值和协方差
mean = self.voxel_means[key]
cov = self.voxel_covs[key]
# 4. 计算残差
delta = p_transformed - mean
# 5. 计算协方差逆矩阵
cov_inv = np.linalg.inv(cov)
# 6. 累加代价:0.5 * delta^T * cov_inv * delta
cost += 0.5 * delta.T @ cov_inv @ delta
n_points += 1
if n_points == 0:
return 1e9 # 无有效点,返回大代价
return cost / n_points # 归一化
def match(self, src_points, ref_points, initial_xi=[0.0, 0.0, 0.0]):
"""
NDT配准主函数
:param src_points: 源点云(待配准)
:param ref_points: 参考点云(目标)
:param initial_xi: 初始变换参数 [tx, ty, theta]
:return: 最优变换参数、变换后的源点云
"""
# 1. 构建参考点云的NDT模型
self.build_ndt_model(ref_points)
# 2. 优化目标函数(使用L-BFGS-B算法)
result = opt.minimize(
fun=self._ndt_cost,
x0=initial_xi,
args=(src_points,),
method='L-BFGS-B',
tol=self.tolerance,
options={'maxiter': self.max_iter, 'disp': True}
)
# 3. 最优变换参数
optimal_xi = result.x
# 4. 变换源点云
src_transformed = np.array([
self._transform_point(p, optimal_xi) for p in src_points
])
return optimal_xi, src_transformed
# ---------------------- 辅助函数:生成测试点云 ----------------------
def generate_test_point_cloud(num_points=1000, translate=[2.0, 1.0], rotate=np.pi/6):
"""生成带平移和旋转的测试点云"""
# 生成随机点云(矩形区域)
x = np.random.uniform(0, 10, num_points)
y = np.random.uniform(0, 10, num_points)
points = np.vstack((x, y)).T
# 应用变换
R = np.array([
[np.cos(rotate), -np.sin(rotate)],
[np.sin(rotate), np.cos(rotate)]
])
points = (R @ points.T).T + np.array(translate)
# 添加少量噪声
points += np.random.normal(0, 0.1, points.shape)
return points
# ---------------------- 可视化函数 ----------------------
def visualize_result(ref_points, src_points, src_transformed):
"""可视化配准结果"""
plt.figure(figsize=(10, 8))
# 绘制参考点云(蓝色)
plt.scatter(ref_points[:, 0], ref_points[:, 1], c='b', s=1, label='Reference Point Cloud')
# 绘制原始源点云(红色)
plt.scatter(src_points[:, 0], src_points[:, 1], c='r', s=1, label='Source Point Cloud (Original)')
# 绘制配准后源点云(绿色)
plt.scatter(src_transformed[:, 0], src_transformed[:, 1], c='g', s=1, label='Source Point Cloud (Registered)')
plt.axis('equal')
plt.grid(True)
plt.legend()
plt.title('NDT Point Cloud Registration Result')
plt.show()
# ---------------------- 测试代码 ----------------------
if __name__ == "__main__":
# 1. 生成测试点云
# 参考点云(无变换)
ref_points = generate_test_point_cloud(num_points=1000, translate=[0, 0], rotate=0)
# 源点云(带平移[2,1]和旋转π/6)
src_points = generate_test_point_cloud(num_points=800, translate=[2.0, 1.0], rotate=np.pi/6)
# 2. 初始化NDT匹配器
ndt_matcher = NDTMatcher2D(
voxel_size=1.0, # 体素大小1m
step_size=0.1, # 优化步长
tolerance=1e-4, # 收敛阈值
max_iter=100 # 最大迭代次数
)
# 3. NDT配准(初始变换设为[0,0,0])
initial_xi = [0.0, 0.0, 0.0]
optimal_xi, src_transformed = ndt_matcher.match(src_points, ref_points, initial_xi)
# 4. 输出结果
print("="*50)
print("NDT配准结果:")
print(f"最优平移 tx: {optimal_xi[0]:.4f}, ty: {optimal_xi[1]:.4f}")
print(f"最优旋转 theta: {optimal_xi[2]:.4f} rad ({np.degrees(optimal_xi[2]):.2f}°)")
print(f"真实平移 tx: 2.0, ty: 1.0")
print(f"真实旋转 theta: {np.pi/6:.4f} rad ({np.degrees(np.pi/6):.2f}°)")
print("="*50)
# 5. 可视化结果
visualize_result(ref_points, src_points, src_transformed)3. 代码关键解释
- 体素划分:_get_voxel_key函数将点映射到整数坐标的体素键,实现空间网格划分;
- NDT 模型构建:build_ndt_model计算每个体素的均值和协方差,添加正则项避免协方差矩阵奇异;
- 位姿变换:_transform_point实现 2D 旋转 + 平移变换,是点云配准的核心操作;
- 目标函数:_ndt_cost实现 NDT 的负对数似然代价计算,是优化的核心;
- 优化求解:使用scipy.optimize.minimize的 L-BFGS-B 算法(适合小维度优化)求解最优变换参数;
- 测试数据:生成带平移和旋转的测试点云,验证 NDT 的配准效果。
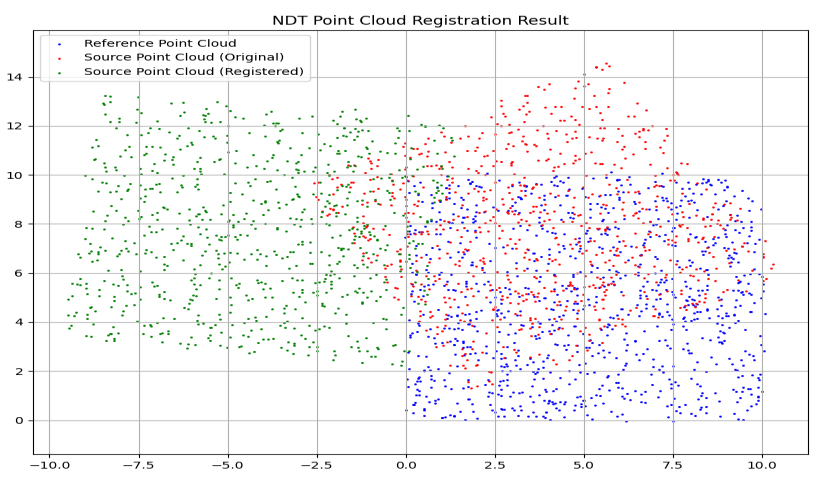
4. 运行结果说明
- 控制台输出最优变换参数与真实参数的对比,NDT 能准确恢复平移和旋转;
- 可视化窗口中:蓝色是参考点云,红色是原始源点云(偏移),绿色是配准后源点云(与参考点云对齐);
- 体素大小是关键参数:体素过大则精度低,过小则计算量大,需根据点云尺度调整。
六、NDT 优缺点分析
| 维度 | 优点 | 缺点 |
|---|---|---|
| 配准效率 | 无需寻找对应点,计算复杂度低(O(n),n为源点云数量) | 体素划分和协方差计算有额外开销(但远低于 ICP) |
| 初始位姿要求 | 对初始位姿要求低于 ICP(允许一定偏移) | 初始位姿偏差过大会导致配准失败(需粗配准) |
| 精度 | 配准精度较高(依赖体素大小和优化算法) | 精度略低于 ICP(尤其是精细配准场景) |
| 鲁棒性 | 对噪声和点云密度变化鲁棒 | 体素内点数量过少时,协方差矩阵不准确,影响配准效果 |
| 维度适配 | 支持 2D/3D 点云,扩展简单 | 3D 下协方差矩阵计算量增加,需优化(如稀疏体素) |
七、NDT 改进方向(工程应用)
- 体素优化:使用自适应体素大小(点密区小体素,点疏区大体素);
- 粗配准 + 精配准:先用 ICP / 特征匹配做粗配准,再用 NDT 做精配准;
- 多分辨率 NDT:先大体积素快速收敛,再小体积素精细优化;
- GPU 加速:体素划分、协方差计算、优化过程 GPU 并行,提升大规模点云配准速度;
- 3D NDT 扩展:将 2D 代码扩展到 3D,变换参数增加绕 x/y/z 轴的旋转(共 6 个参数)。
八、结束语
- 核心逻辑:NDT 将参考点云转为概率密度模型,通过优化使源点云在该模型中的概率最大化,实现配准;
- 数学核心:多维正态分布的概率密度函数是 NDT 的理论基础,目标函数是负对数似然的简化形式;
- 工程关键:体素大小、协方差正则化、优化算法是影响 NDT 配准效果的核心参数;
- 适用场景:大规模点云、实时配准、对初始位姿有一定偏差的场景(如自动驾驶激光雷达配准)。