【一百】【算法分析与设计】N皇后问题常规解法+位运算解法

N皇后问题

链接：登录---专业IT笔试面试备考平台_牛客网来源：牛客网

题目描述

给出一个n×nn\times nn×n的国际象棋棋盘，你需要在棋盘中摆放nnn个皇后，使得任意两个皇后之间不能互相攻击。具体来说，不能存在两个皇后位于同一行、同一列，或者同一对角线。请问共有多少种摆放方式满足条件。

输入描述:

一行，一个整数n(1≤n≤12)n(1\le n \le 12)n(1≤n≤12)，表示棋盘的大小。

输出描述:

输出一行一个整数，表示总共有多少种摆放皇后的方案，使得它们两两不能互相攻击。

示例1

输入

复制4

4

输出

复制2

2

常规解法

复制代码

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;

#define int long long
#define endl '\n'
#define Fast() ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);

#define p pair<int,int>
#define ff first
#define ss second 
#define pb push_back
#define ppb pop_back

#define ltu(i,a,b) for(int i=a;i<=b;i++) // 定义从a到b的循环
#define utl(i,a,b) for(int i=a;i>=b;i--) // 定义从a到b的倒序循环
#define tests() int t;cin>>t;while(t--) // 读取测试次数并循环

int n; // 棋盘的大小
int ret=0; // 解的数量
vector<bool> visited1; // 列的标记数组
vector<bool> visited2; // 左下到右上的斜线标记数组
vector<bool> visited3; // 右下到左上的斜线标记数组

void dfs(int i){ // 深度优先搜索函数，i表示当前行
    ltu(j,1,n){ // 遍历第i行的每一列
        if(!visited1[j]&&!visited2[j-i+n]&&!visited3[j+i]){ // 如果第j列和两条斜线都没有被占用
            if(i==n){ // 如果已经放到最后一行
                ret++; // 解的数量加一
                continue; // 继续下一次循环
            }
            visited1[j]=visited2[j-i+n]=visited3[j+i]=true; // 标记当前列和斜线
            dfs(i+1); // 递归调用下一行
            visited1[j]=visited2[j-i+n]=visited3[j+i]=false; // 回溯，取消标记
        }
    }
}

void solve(){ // 解决函数
    ret=0; // 重置解的数量
    visited1.assign(n+1,0); // 初始化列标记数组
    visited2.assign(2*n+1,0); // 初始化左下到右上的斜线标记数组
    visited3.assign(2*n+1,0); // 初始化右下到左上的斜线标记数组
    dfs(1); // 从第一行开始搜索
    cout<<ret<<endl; // 输出解的数量
}

signed main(){ // 主函数
    Fast(); // 加速输入输出
    
    cin>>n; // 读取棋盘大小
    solve(); // 调用解决函数
}

位运算解法1

复制代码

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;

#define int long long // 定义 int 为 long long 类型
#define endl '\n' // 定义 endl 为换行符
#define Fast() ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); // 快速输入输出

#define p pair<int,int> // 定义 p 为一对整数
#define ff first // 定义 ff 为 first
#define ss second // 定义 ss 为 second 

#define ltu(i,a,b) for(int i=a;i<=b;i++) // 定义从 a 到 b 的递增循环
#define utl(i,a,b) for(int i=a;i>=b;i--) // 定义从 a 到 b 的递减循环
#define tests() int t;cin>>t;while(t--) // 定义测试次数循环

int n; // 定义 n
int ret=0; // 定义 ret 并初始化为 0
int col, leftt, rightt; // 定义 col, leftt, rightt 记录有皇后的位置

// 深度优先搜索函数
void dfs(int i, int col, int leftt, int rightt) {
    if (i == n + 1) { // 如果已经放置完所有皇后
        ret++; // 计数增加
        return; // 返回上一层
    }
    // 从第 0 列到第 n-1 列尝试放置皇后
    ltu(j, 0, n-1) {
        // 检查第 j 列，左斜和右斜是否被攻击
        bool temp = (col & (1 << j)) | (leftt & (1 << (i - j + n))) | (rightt & (1 << (i + j)));
        if (!temp) { // 如果当前位置没有被攻击
            // 递归调用下一行，更新 col, leftt 和 rightt
            dfs(i + 1, col | (1 << j), leftt | (1 << (i - j + n)), rightt | (1 << (i + j)));
        }
    }
}

// 解决问题的函数
void solve() {
    col = leftt = rightt = 0; // 初始化 col, leftt 和 rightt
    dfs(1, col, leftt, rightt); // 调用 dfs 函数从第 1 行开始
    cout << ret << endl; // 输出结果
}

signed main() {
    Fast(); // 快速输入输出
    
    cin >> n; // 输入 n
    solve(); // 调用 solve 函数
}

位运算解法2

复制代码

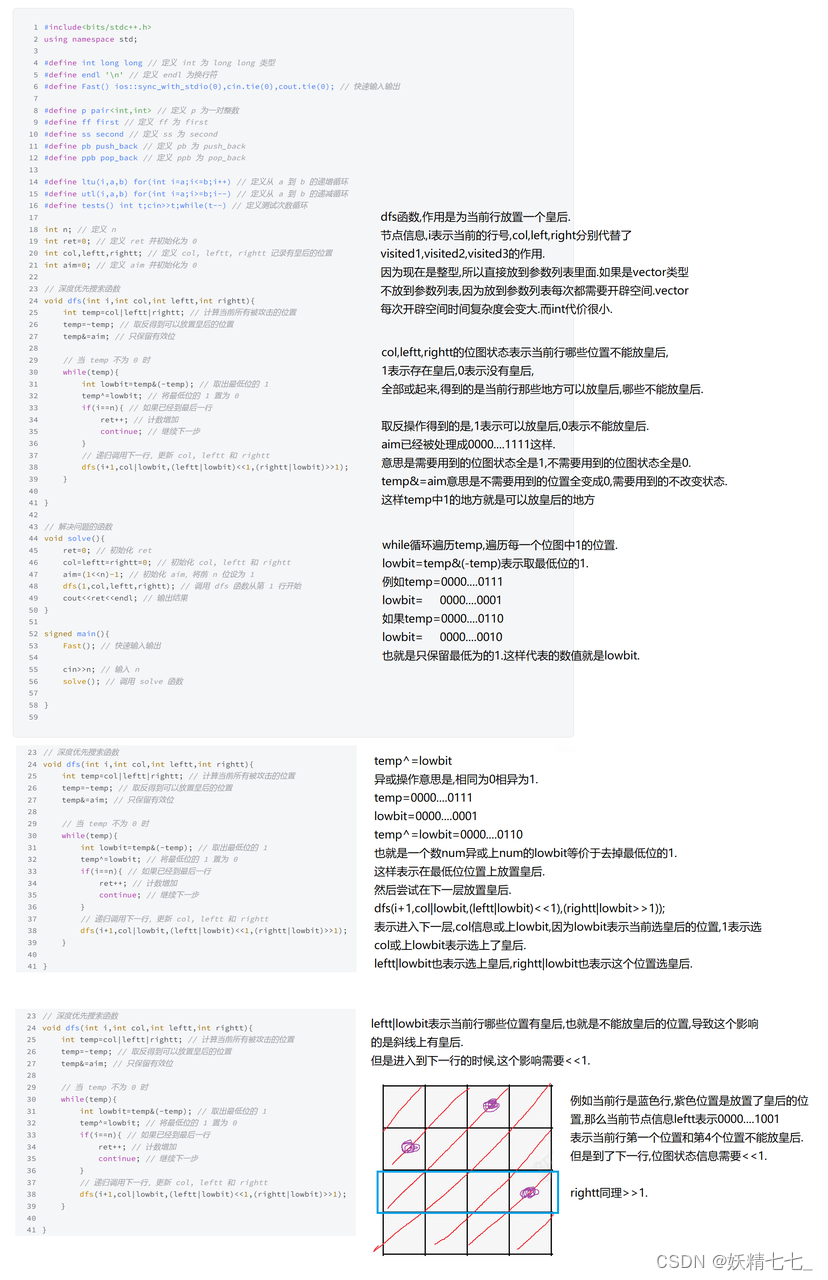
cpp 复制代码

#include<bits/stdc++.h>
using namespace std;

#define int long long // 定义 int 为 long long 类型
#define endl '\n' // 定义 endl 为换行符
#define Fast() ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); // 快速输入输出

#define p pair<int,int> // 定义 p 为一对整数
#define ff first // 定义 ff 为 first
#define ss second // 定义 ss 为 second
#define pb push_back // 定义 pb 为 push_back
#define ppb pop_back // 定义 ppb 为 pop_back

#define ltu(i,a,b) for(int i=a;i<=b;i++) // 定义从 a 到 b 的递增循环
#define utl(i,a,b) for(int i=a;i>=b;i--) // 定义从 a 到 b 的递减循环
#define tests() int t;cin>>t;while(t--) // 定义测试次数循环

int n; // 定义 n
int ret=0; // 定义 ret 并初始化为 0
int col,leftt,rightt; // 定义 col, leftt, rightt 记录有皇后的位置
int aim=0; // 定义 aim 并初始化为 0

// 深度优先搜索函数
void dfs(int i,int col,int leftt,int rightt){
    int temp=col|leftt|rightt; // 计算当前所有被攻击的位置
    temp=~temp; // 取反得到可以放置皇后的位置
    temp&=aim; // 只保留有效位

    // 当 temp 不为 0 时
    while(temp){
        int lowbit=temp&(-temp); // 取出最低位的 1
        temp^=lowbit; // 将最低位的 1 置为 0
        if(i==n){ // 如果已经到最后一行
            ret++; // 计数增加
            continue; // 继续下一步
        }
        // 递归调用下一行，更新 col, leftt 和 rightt
        dfs(i+1,col|lowbit,(leftt|lowbit)<<1,(rightt|lowbit)>>1);
    }
    
}

// 解决问题的函数
void solve(){
    ret=0; // 初始化 ret
    col=leftt=rightt=0; // 初始化 col, leftt 和 rightt
    aim=(1<<n)-1; // 初始化 aim，将前 n 位设为 1
    dfs(1,col,leftt,rightt); // 调用 dfs 函数从第 1 行开始
    cout<<ret<<endl; // 输出结果
}

signed main(){
    Fast(); // 快速输入输出
    
    cin>>n; // 输入 n
    solve(); // 调用 solve 函数
    
}

结尾

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。

谢谢您的支持，期待与您在下一篇文章中再次相遇！