基于小波分析的一维时间序列多重分形分析（MATLAB R2018a）

分形与小波变换在尺度性能上具有很多相似性，因此小波变换被认为是分析、刻画分形现象一个有力的工具。在分析分形的一般方法中，需要按照"盒维数"的计算思想，首先要将研究序列进行不同长度的分割，然后建立起结构函数，再研究结构函数与尺度之间的变化关系，若是多重分形分析则还要通过不同大小的幂次方操作将不同奇异点集区分开来。鉴于分形与小波之间在尺度上的相似性，应用小波来研究分形不需要再对序列进行分割，因为通过小波变换即可得到不同尺度上用于构建结构函数所需要的元素。

无论是连续小波变换还是离散小波变换，小波系数均能刻画出序列在不同时点上、不同尺度上的局部特征。因此，分形既然在不同尺度上具有自相似性，那么应用"显微镜"式的小波分析在不同放大倍数（尺度）的镜片下来考察系统的分形特性最自然不过了。

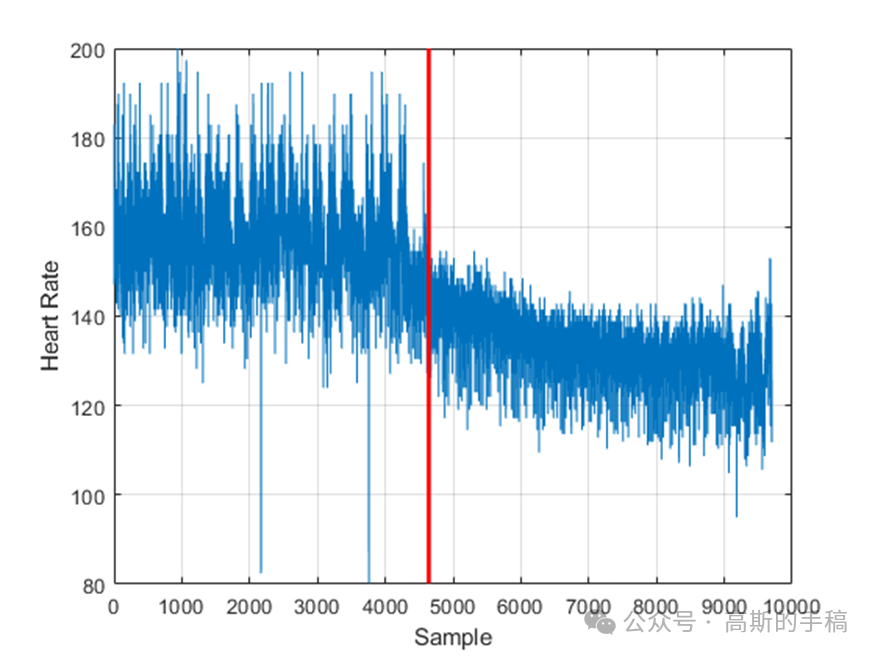
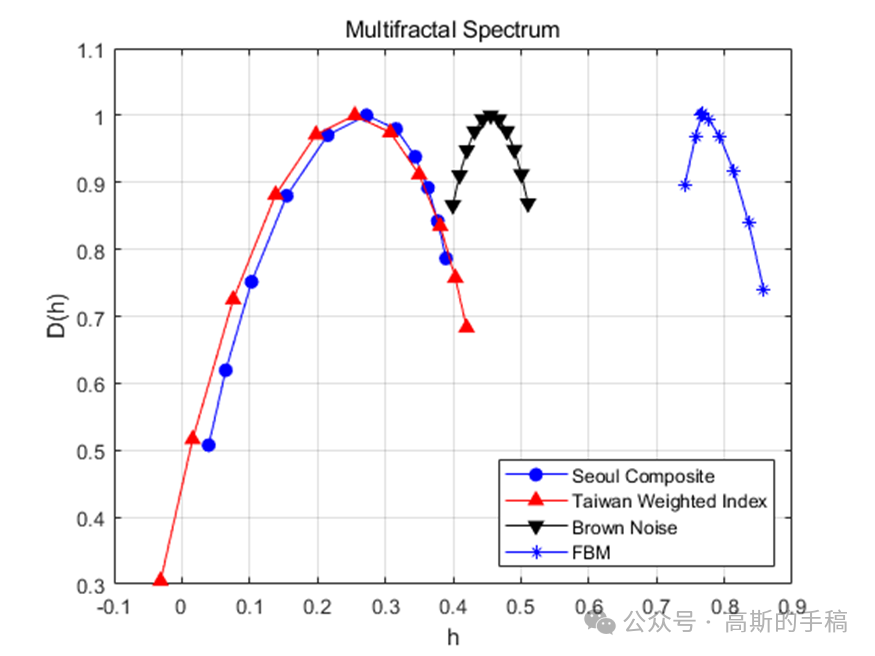
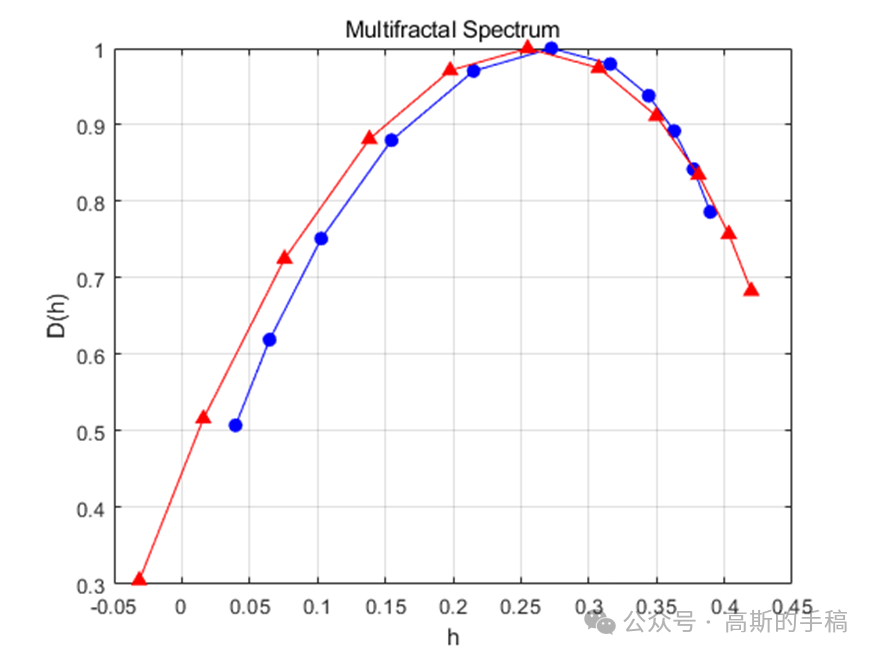
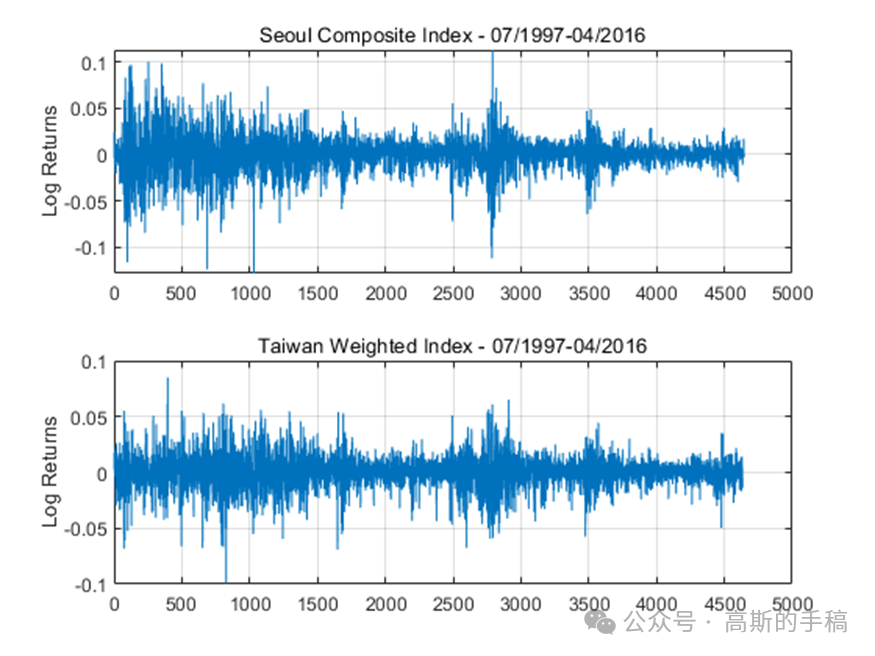
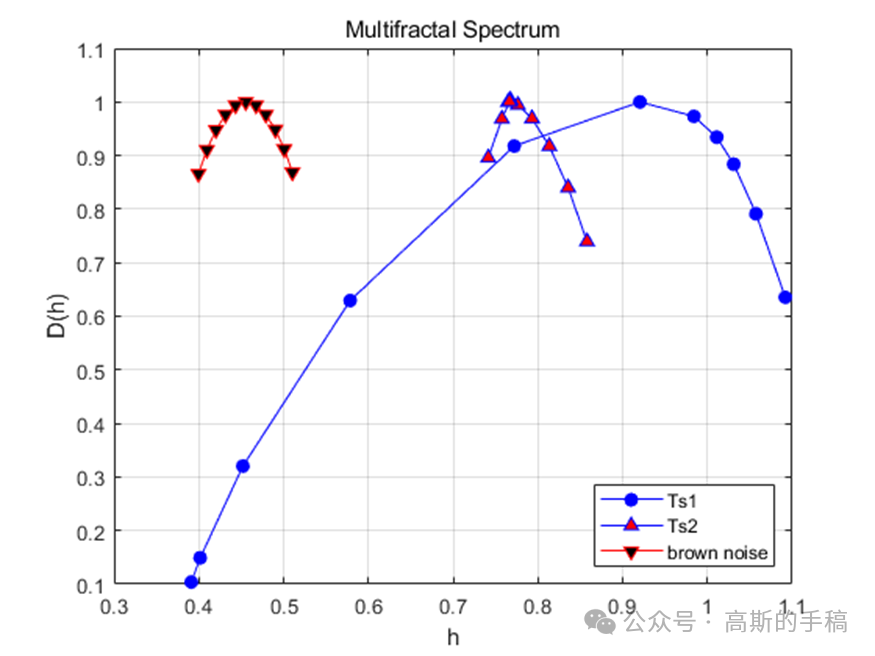
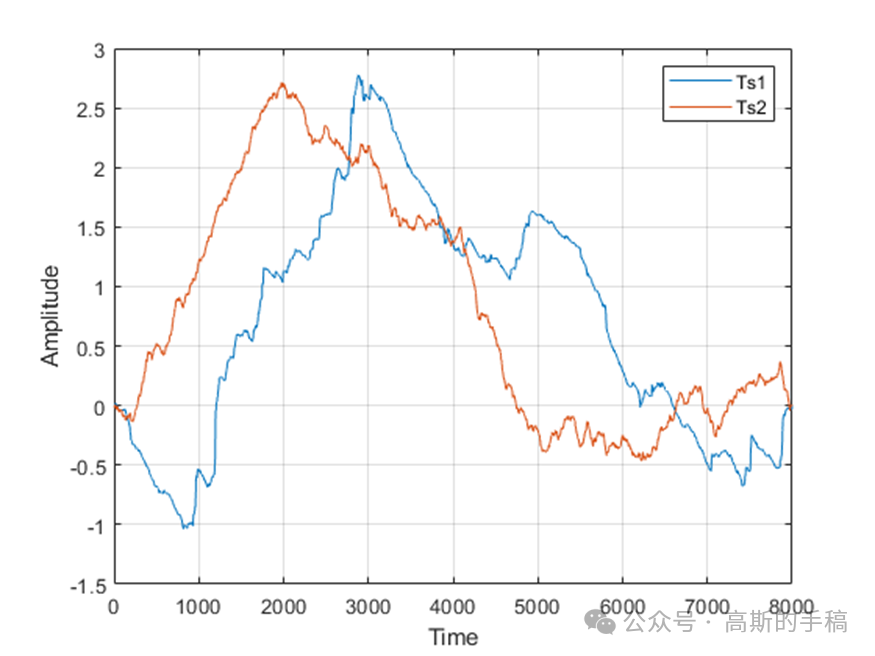
鉴于此，采用小波分析方法对一维时间序列进行多重分形分析，使用小波分形技术来表征局部信号的规则性，并给出几个例子，比如布朗过程，股票综合数据等。算法可迁移至金融时间序列，地震/微震信号，机械振动信号，声发射信号，电压/电流信号，语音信号，声信号，生理信号（ECG,EEG,EMG）等一维时间序列信号。程序运行环境为MATLAB R2018A。

Matlab 复制代码

function params = parseinputs(varargin)

params.wname = 'bior1.5';
params.j1 = 3;
params.q = -5:5;
params.cumulant = 3;
params.weight = 'uniform';
if isempty(varargin)
    return;
end

tf = find(strncmpi(varargin,'MinRegressionLevel',2));
if nnz(tf) == 1
    params.j1 = varargin{tf+1};
    validateattributes(params.j1,{'numeric'},{'scalar','integer', '>=',2},...
        'dwtleader','MinRegressionLevel');
    varargin(tf:tf+1) = [];
    if isempty(varargin)
        return;
    end
end

tf = find(strncmpi(varargin,'MaxRegressionLevel',2));
if nnz(tf) == 1
    params.J = varargin{tf+1};
    validateattributes(params.J,{'numeric'},{'scalar','integer', ...
        '>=',params.j1+1},'dwtleader','MaxRegressionLevel');
    varargin(tf:tf+1) = [];
    if isempty(varargin)
        return;
    end
end

tf = find(strncmpi(varargin,'RegressionWeight',1));
if nnz(tf) == 1
    params.weight = varargin{tf+1};
    validweights = {'uniform','scale'};
    params.weight = validatestring(params.weight,validweights);
    varargin(tf:tf+1) = [];
    if isempty(varargin)
        return;
    end
end

% Only remaining varargin argument must be wavelet
tf = cellfun(@(x)ischar(x),varargin);
if nnz(tf) == 1
    params.wname = varargin{tf>0};
    varargin(tf>0) = [];
else
    error('Invalid');
end

完整代码：https://mbd.pub/o/bread/mbd-ZJWZm5ps

if ~isempty(varargin)
    error(message('Wavelet:mfa:UnsupportedSyntax'));
end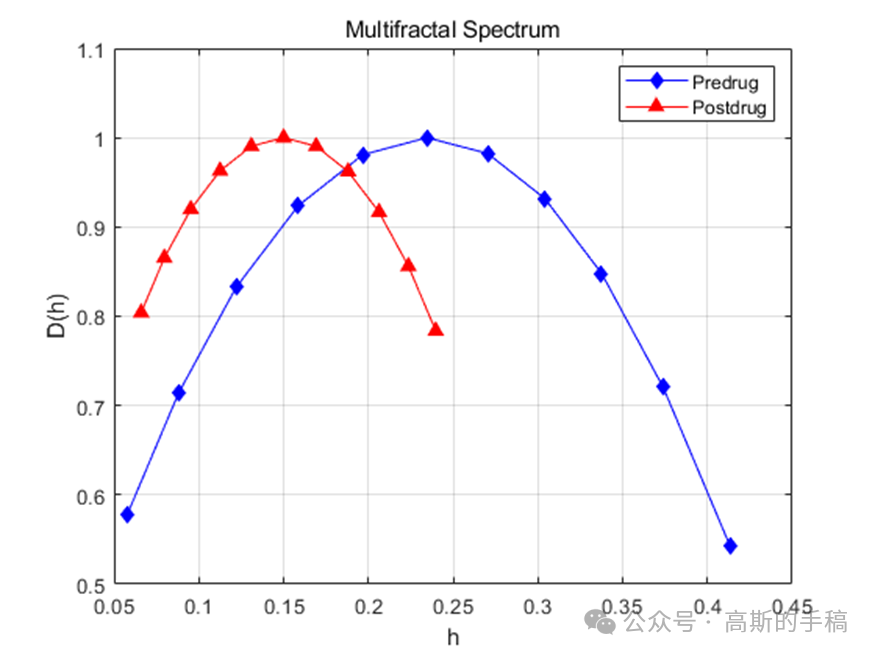

工学博士，担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家，擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。