前缀和
定义：
前缀和是指某序列的前n项和，可以把它理解为数学上的数列的前n项和，而差分可以看成前缀和的逆运算。合理的使用前缀和与差分，可以将某些复杂的问题简单化。
用途：
前缀和一般用于统计一个区间的和，为的就是可以将区间和问题的时间复杂度降低，从而节约时间
样例：
假如说我们有一个数组，数组里面有n个元素，给你m个访问，每次给你一个L和R，问你L和R这个区间内的元素的和为多少
我们首先想到的暴力解法应该是每次调用一次for循环，去遍历区间的元素，然后求和，但是这样的时间复杂度在最坏的情况下会达到O(n*m)的时间复杂度，对于大数据来说，这种肯定是要超时的，因此我们可以用到我们的前缀和
首先，我们可以用一个前缀和数组统计出现的和，pre[ i ]放的就是在 i 之前的所有数的和，每次询问，只需要输出pre[ R ] - pre[ L - 1 ]即可，时间复杂度为O(n+m)，这样就大大减小的时间复杂度
因此我们可以看到前缀和在多次求解区间和问题上的优势。
一维前缀和
在一维空间内的统计十分简单，只需要设计一个一维pre数组即可
一维前缀和预处理公式
pre[i]=pre[i-1]+a[i];
区间求解公式（从L到R的区间）
pre[R]-pre[L-1]
来看例题
题解：很标准的前缀和问题，每次询问的都是一个区间的和，那么我们直接用一维前缀和即可
cpp
#include<bits/stdc++.h>
using namespace std;
int n;
int a[100005];
int m;
int pre[100005];
int l,r;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
pre[i]=pre[i-1]+a[i];
}
cin>>m;
for(int i=1;i<=m;i++)
{
cin>>l>>r;
cout<<pre[r]-pre[l-1]<<"\n";
}
return 0;
} 二维前缀和
二维前缀和的计算是基于容斥原理的，我们需要通过对矩阵面积的划分计算来的出二维前缀和的预处理公式和求和公式
预处理公式：
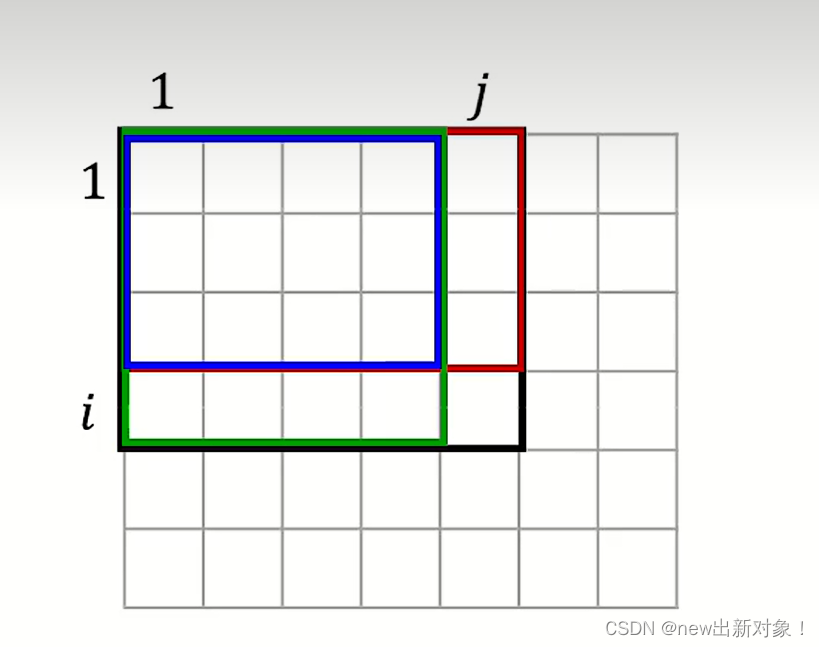
我们通过这个图来了解，二维前缀和的预处理公式，首先我们将元素变成矩阵的一个一个的小方块，我们看如何去求第i行第j列之前的面积，首先我们的矩阵面积可以S(i-1,j)+S(i,j-1)的面积之和，但是多了一部分重叠部分S(i-1,j-1),并且加上额外的有下角元素a(i,j)，因此我们的预处理公式就可以得出：
pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+a[i][j];
二维前缀和求和公式：
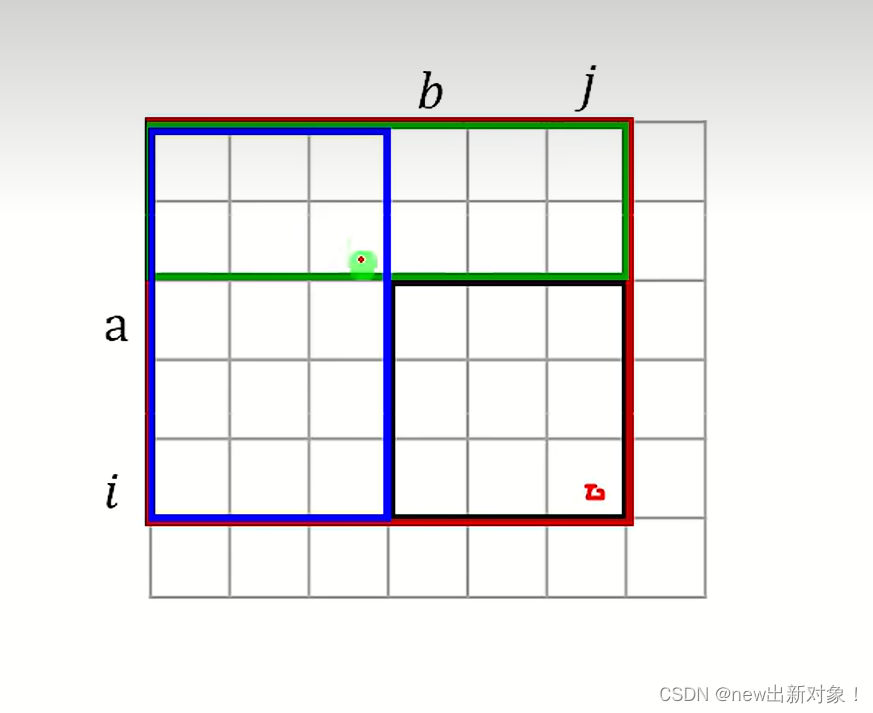
也是将计算变为矩阵面积来看，假如说我们想算从(a,b)到(i,j)的前缀和，我们首先可以用整个的大面积( S(i,j) )的面积减去S(a-1,j)和S(i,b-1)，但是通过容斥原理发现我们多减一部分，那就是
S(a-1,b-1)，因此我们就可以得出二维前缀和求和公式：
pre[i][j]-pre[a-1][j]-pre[i][b-1]+pre[a-1][b-1]
我们来看一道例题：最大加权矩阵
这道题，一眼就能看出来是二维前缀和，但是由于数据比较小，所以可以暴力枚举其范围，总共四重循环，计算其中前缀和的最大矩阵和，最后输出即可
cpp
#include<bits/stdc++.h>
using namespace std;
int n;
int a[125][125];
int pre[125][125];
signed main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
cin>>a[i][j];
pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+a[i][j];
}
}
int ans=-0x3f3f3f3f;
for(int x1=1;x1<=n;x1++)
{
for(int y1=1;y1<=n;y1++)
{
for(int x2=x1;x2<=n;x2++)
{
for(int y2=y1;y2<=n;y2++)
{
ans=max(ans,pre[x2][y2]-pre[x1-1][y2]-pre[x2][y1-1]+pre[x1-1][y1-1]);
}
}
}
}
cout<<ans;
return 0;
}
题解，就是一个二维前缀和模版，很简单，直接写就OK了，只需要记录其中的左上角坐标就OK
cpp
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,c;
int a[1005][1005];
int pre[1005][1005];
int ans=-0x3f3f3f3f3f3f3f3f;
int x,y;
signed main()
{
cin>>n>>m>>c;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cin>>a[i][j];
pre[i][j]=pre[i-1][j]+pre[i][j-1]-pre[i-1][j-1]+a[i][j];
}
}
for(int i=c;i<=n;i++)
{
for(int j=c;j<=m;j++)
{
if(ans<pre[i][j]-pre[i-c][j]-pre[i][j-c]+pre[i-c][j-c])
{
ans=pre[i][j]-pre[i-c][j]-pre[i][j-c]+pre[i-c][j-c];
x=i;
y=j;
}
}
}
cout<<x-c+1<<" "<<y-c+1;
return 0;
}前缀和的应用（包括二分思想，这里默认各位看官老爷都会）
题意：就是说给你n个矿石，然后，这n个矿石都有自己的重量w，以及其价值v，我们有一种判断机制，就是说给你m个区间范围，每次给你一个左边界L和右边界R，我们的计算机理是，这个区间内的大于规定筛选重量W的数量，乘以大于筛选重量的价值,然后将总的算出来的y累加到一起，看看和规定的标准值S最小差多少，输出最小的参数W
思路，我们发现这题数据超大，必然会有优化方法，我们通过上面·的题意可以发现，我们的参数设置的越大，能过筛选的石头越少，得到的y值越小，设置的越小，能筛选过的石头越多，得到的y值越大,因此我们可以用二分（二分的范围就是给的数据的石头的最小值到最大值，但是我们还要扩增范围，最小值减一，最大值加二）然后我们每次二分的就是参数W，然后在计算过程中要用到前缀和优化，我们要去记录出现的大于参数的矿石数目以及总价值，然后我们去计算总的Y值，Y值大于标准值S就说明，我们的参数设置的小了，要增大左边界，要是小于标准值，就说明，我们的参数设置的太大了，要缩小右边界
cpp
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,s;
int w[200005];
int v[200005];
int l[200005],r[200005];
int maxn=0;
int minn=0x3f3f3f3f3f3f3f3f;
int sumn[200005];
int sumv[200005];
int ans=0;//统计本次筛选的总价值
int mn=0x3f3f3f3f3f3f3f3f;//统计最小差值
bool check(int mid)
{
memset(sumn,0,sizeof(sumn));
memset(sumv,0,sizeof(sumv));
int ans=0;//统计总的价值也就是y[i]
for(int i=1;i<=n;i++)
{
if(w[i]>=mid)
{
sumn[i]=sumn[i-1]+1;//统计能过筛查的数量
sumv[i]=sumv[i-1]+v[i];//统计能过筛查的价值
}
else
{
sumn[i]=sumn[i-1];
sumv[i]=sumv[i-1];
}
}
for(int i=1;i<=m;i++)
{
ans+=(sumn[r[i]]-sumn[l[i]-1])*(sumv[r[i]]-sumv[l[i]-1]);
}
mn=min(mn,llabs(ans-s));
if(ans>s)
return true;
return false;
}
signed main()
{
cin>>n>>m>>s;
for(int i=1;i<=n;i++)
{
cin>>w[i]>>v[i];
maxn=max(maxn,w[i]);//二分的上下边界
minn=min(minn,w[i]);
}
int left,right,mid;
for(int i=1;i<=m;i++)
{
cin>>l[i]>>r[i];
}
left=minn-1,right=maxn+2;
while(left<=right)
{
mid=(left+right)/2;
if(check(mid))
{
left=mid+1;
}
else
{
right=mid-1;
}
}
cout<<mn;
return 0;
}