深入浅出3D感知中的优化与基于学习的技术 (第三章:基于循环全对场变换的光流估计) 原创教程
本系列禁止转载,有技术探讨可以发邮件给我 fanzexuan135@163.com
RAFT - 基于循环全对场变换的光流估计
光流是估计视频帧之间每个像素运动的任务。这是一个长期存在的视觉问题,至今仍未完全解决。最好的系统仍然受到快速移动物体、遮挡、运动模糊和无纹理表面等困难的限制。
传统上,光流被视为一个在一对图像之间的稠密位移场上的手工优化问题[21,51,13]。通常,优化目标定义了一个折衷,在鼓励视觉相似区域对齐的数据项和对运动合理性施加先验的正则化项之间取得平衡。这种方法已经取得了相当大的成功,但进一步的进展似乎很有挑战性,因为手工设计一个对各种复杂情况都很robust的目标函数是很困难的。
最近,深度学习已被证明是传统方法的一个有前途的替代方案。深度学习可以避开优化问题的公式化,直接训练一个网络来预测光流。目前的深度学习方法[25,42,22,49,20]已经达到了与最好的传统方法相当的性能,同时在推理时间上显著更快。进一步研究的一个关键问题是设计有效的架构,以获得更好的性能,更容易训练,并能很好地泛化到新场景。
我们引入了RAFT(Recurrent All-Pairs Field Transforms),这是一种新的端到端可训练的光流深度网络架构。RAFT具有以下优势:
-
最先进的准确性:在KITTI[18]上,RAFT实现了5.10%的F1-all误差,比已发表的最佳结果(6.10%)降低了16%的误差。在Sintel[11](final pass)上,RAFT获得了2.855像素的端点误差,比已发表的最佳结果降低了30%的误差。
-
强泛化能力:当仅在合成数据上训练时,RAFT在KITTI[18]上实现了5.04像素的端点误差,比在相同数据上训练的最佳先前深度网络(8.36像素)降低了40%的误差。
-
高效性:RAFT在1080Ti GPU上以每秒10帧的速度处理1088×436的视频。它的训练迭代次数比其他架构少10倍。RAFT的一个更小版本,参数量只有1/5,运行速度为每秒20帧,同时仍然优于所有先前的方法。
RAFT由三个主要部分组成:(1)特征编码器,为每个像素提取特征向量;(2)相关层,为所有像素对生成4D相关体,然后池化以生成低分辨率的相关体;(3)基于GRU的循环更新算子,从相关体中检索值并迭代更新初始化为零的流场。图3.1说明了RAFT的设计。
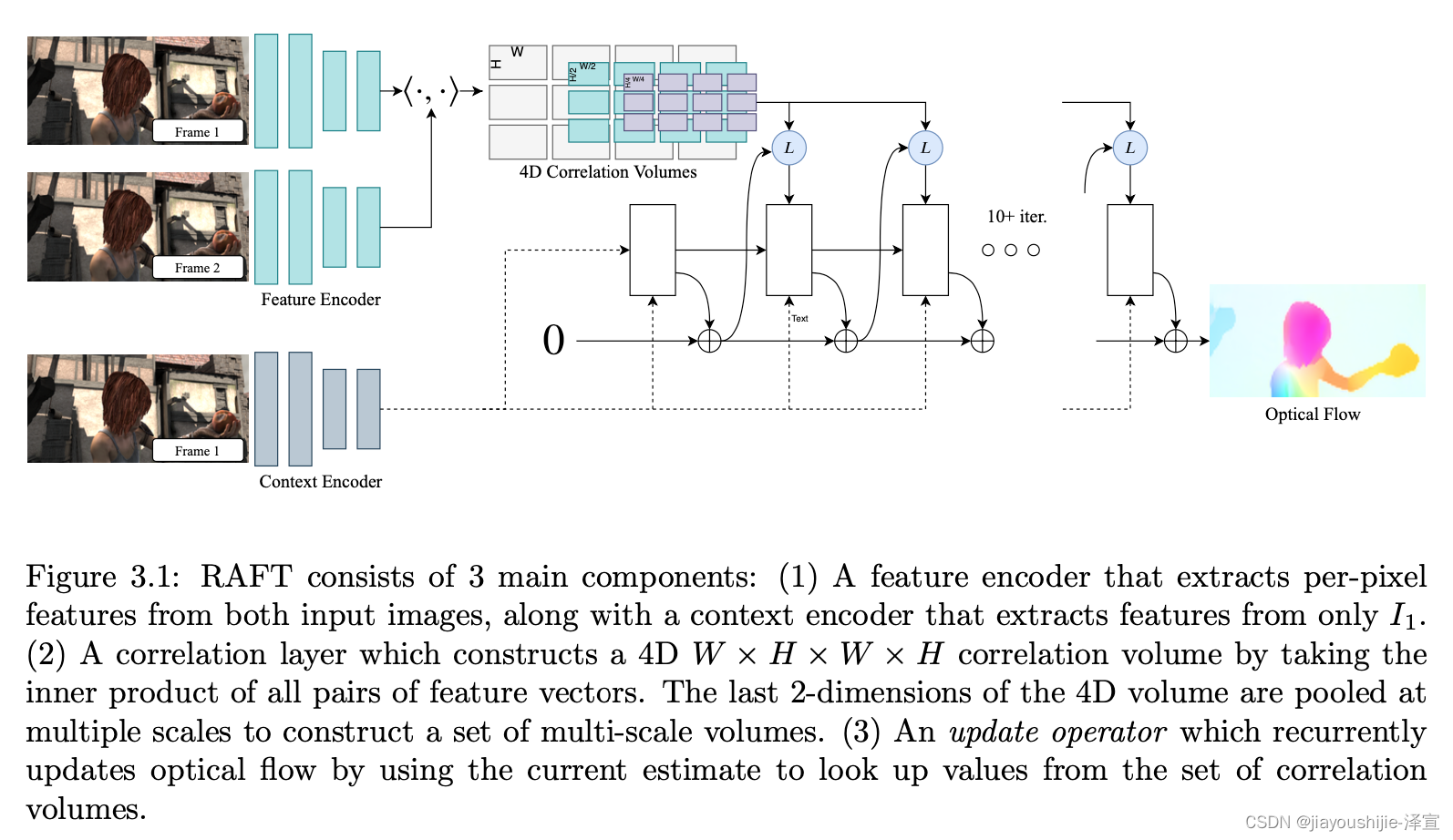
RAFT的架构的灵感来自传统的基于优化的方法。特征编码器提取每像素特征。相关层计算像素之间的视觉相似度。更新算子模仿迭代优化算法的步骤。但与传统方法不同的是,特征和运动先验不是手工设计的,而是学习得到的------分别由特征编码器和更新算子学习。
RAFT的设计借鉴了许多现有工作,但有实质性的创新。首先,RAFT维护和更新单个高分辨率的固定流场。这与先前工作中流行的coarse-to-fine设计不同[42,49,22,23,50],后者首先在低分辨率估计流,然后在高分辨率进行上采样和细化。通过对单个高分辨率流场进行操作,RAFT克服了coarse-to-fine级联的几个局限性:在粗分辨率下难以从错误中恢复,容易错过快速移动的小物体,以及通常需要许多训练迭代(通常超过1M)来训练多阶段级联。
其次,RAFT的更新算子是循环且轻量级的。最近的许多工作[24,42,49,22,25]都包含某种形式的迭代细化,但不会在迭代之间共享权重[42,49,22],因此仅限于固定次数的迭代。据我们所知,IRR[24]是唯一的循环深度学习方法[24]。它使用FlowNetS[15]或PWC-Net[42]作为其循环单元。当使用FlowNetS时,它受到网络大小的限制(38M参数),最多只能应用5次迭代。当使用PWC-Net时,迭代次数受金字塔级数限制。相比之下,我们的更新算子只有2.7M个参数,在推理期间可以应用100多次而不会发散。
第三,更新算子采用了新颖的设计,由一个卷积GRU组成,它对4D多尺度相关体执行查找;相比之下,先前工作中的细化模块通常只使用普通卷积或相关层。
我们在Sintel[11]和KITTI[18]上进行了实验。结果表明,RAFT在这两个数据集上都达到了最先进的性能。此外,我们通过广泛的消融研究验证了RAFT的各种设计选择。
3.1 相关工作
作为能量最小化的光流 光流传统上被视为一个能量最小化问题,在数据项和正则化项之间施加权衡。Horn和Schnuck[21]使用变分框架将光流公式化为连续优化问题,并通过执行梯度步骤来估计稠密流场。Black和Anandan[9]通过引入稳健估计框架来解决过度平滑和噪声敏感性问题。TV-L1[51]用L1数据项和总变分正则化替换了二次惩罚,允许运动不连续性,更好地处理异常值。通过更好的匹配代价[45,10]和正则化[38]已经取得了改进。
这种连续公式维护光流的单个估计值,在每次迭代时进行细化。为确保目标函数平滑,使用一阶泰勒近似来模拟数据项。因此,它们只适用于小位移。为了处理大位移,使用coarse-to-fine策略,其中使用图像金字塔在低分辨率估计大位移,然后在高分辨率细化小位移。但这种coarse-to-fine策略可能会错过快速移动的小物体,并难以从早期错误中恢复。与连续方法一样,我们维护光流的单个估计,并在每次迭代中进行细化。然而,由于我们为高分辨率和低分辨率构建所有对的相关体,每次局部更新都使用关于小位移和大位移的信息。此外,我们的更新算子学习提出下降方向,而不是使用数据项的亚像素泰勒近似。
最近,光流也被视为使用全局目标的离散优化问题[35,13,47]。这种方法的一个挑战是搜索空间的巨大规模,因为每个像素都可以合理地与另一帧中的数千个点配对。Menez等[35]使用特征描述符修剪搜索空间,并使用消息传递近似全局MAP估计。Chen等[13]表明,通过使用距离变换,在完整的流场空间上求解全局优化问题是可行的。DCFlow[47]通过使用神经网络作为特征描述符,并在所有特征对上构建4D代价体,显示了进一步的改进。然后使用Semi-Global Matching(SGM)算法[19]处理4D代价体。像DCFlow一样,我们也在学习到的特征上构建4D代价体。然而,我们使用神经网络来估计流,而不是使用SGM处理代价体。我们的方法是端到端可微分的,这意味着特征编码器可以与网络的其余部分一起训练,以直接最小化最终流估计的误差。相比之下,DCFlow需要使用像素之间的嵌入损失来训练网络;它不能直接在光流上训练,因为其代价体处理不可微。
直接流预测 神经网络已被训练来直接预测一对帧之间的光流,完全避开了优化问题。coarse-to-fine处理已成为最近许多工作中流行的成分[42,50,22,23,24,49,20,8,52]。相比之下,我们的方法维护并更新单个高分辨率流场。
用于光流的迭代细化 最近的许多工作使用迭代细化来改善光流[25,39,42,22,49]和相关任务[29,53,44,28]的结果。Ilg等[25]通过串联多个FlowNetS和FlowNetC模块将迭代细化应用于光流。SpyNet[39],PWC-Net[42],LiteFlowNet[22]和VCN[49]使用coarse-to-fine金字塔应用迭代细化。这些方法与我们的主要区别在于它们不在迭代之间共享权重。
与我们的方法更相关的是IRR[24],它建立在FlownetS和PWC-Net架构之上,但在细化网络之间共享权重。当使用FlowNetS时,它受到网络大小的限制(38M参数),最多只能应用5次迭代。当使用PWC-Net时,迭代次数受金字塔级数限制。相比之下,我们使用一个更简单的细化模块(2.7M参数),在推理期间可以应用100多次而不会发散。我们的方法与Devon[31]也有相似之处,即在不进行warp的情况下构建代价体和固定分辨率更新。然而,Devon没有任何循环单元。它在处理大位移方面也与我们不同。Devon使用dilated代价体处理大位移,而我们的方法在多个分辨率对相关体进行池化。
我们的方法也与TrellisNet[5]和Deep Equilibrium Models(DEQ)[6]有关联。Trellis net在大量层上使用深度绑定权重,DEQ通过直接求解不动点来模拟无限层。TrellisNet和DEQ是为序列建模任务设计的,但我们采用了使用大量权重绑定单元的核心思想。我们的更新算子使用修改的GRU块[14],类似于TrellisNet中使用的LSTM块。我们发现这种结构允许我们的更新算子更容易收敛到固定流场。
学习优化 视觉中的许多问题可以表述为优化问题。这激励了几项工作将优化问题嵌入到网络架构中[4,3,43,32,44]。这些工作通常使用网络来预测优化问题的输入或参数,然后通过求解器反向传播梯度来训练网络权重,要么隐式[4,3],要么展开每一步[32,43]。然而,这种技术仅限于具有容易定义的目标的问题。
另一种方法是直接从数据中学习迭代更新[1,2]。这些方法的动机是第一阶优化器如Primal Dual Hybrid Gradient(PDHG)[12]可以表示为一系列迭代更新步骤。Adler等[1]提出构建一个模仿第一阶算法更新的网络,而不是直接使用优化器。这种方法已应用于逆问题,如图像去噪[26]、断层扫描重建[2]和新视图合成[17]。TVNet[16]将TV-L1算法实现为计算图,可以训练TV-L1参数。然而,TVNet直接基于强度梯度运行,而不是学习的特征,这限制了在Sintel等具有挑战性的数据集上可实现的准确性。
我们的方法可以看作是学习优化:我们的网络使用大量更新块来模拟第一阶优化算法的步骤。然而,与先前的工作不同,我们从不显式定义相对于某些优化目标的梯度。相反,我们的网络从相关体中检索特征来提出下降方向。
3.2 方法
给定一对连续的RGB图像 I 1 , I 2 I_1,I_2 I1,I2,我们估计一个稠密的位移场 ( f 1 , f 2 ) (f_1,f_2) (f1,f2),将 I 2 I_2 I2中的每个像素 ( u , v ) (u,v) (u,v)映射到其在 I 1 I_1 I1中的对应坐标 ( u ′ , v ′ ) = ( u + f 1 ( u ) , v + f 2 ( v ) ) (u',v')=(u+f_1(u),v+f_2(v)) (u′,v′)=(u+f1(u),v+f2(v))。
我们的方法概述如图3.1所示。我们的方法可以归结为三个阶段:(1)特征提取,(2)计算视觉相似度,(3)迭代更新,其中所有阶段都是可微分的,并组成端到端可训练的架构。
3.2.1 特征提取
使用卷积网络从输入图像中提取特征。特征编码器网络应用于 I 1 I_1 I1和 I 2 I_2 I2,并将输入图像映射到低分辨率的稠密特征图。我们的编码器 g θ g_\theta gθ输出1/8分辨率的特征 g θ : R H × W × 3 ↦ m a t h b b R H / 8 × W / 8 × D g_\theta:\mathbb{R}^{H\times W\times 3}\mapsto\\mathbb{R}^{H/8\times W/8\times D} gθ:RH×W×3↦mathbbRH/8×W/8×D,我们设置 D = 256 D=256 D=256。特征编码器由6个残差块组成,2个在1/2分辨率,2个在1/4分辨率,2个在1/8分辨率。
我们还使用了一个上下文网络。上下文网络仅从第一个输入图像 I 1 I_1 I1中提取特征。上下文网络的架构 h θ h_\theta hθ与特征提取网络相同。特征网络 g θ g_\theta gθ和上下文网络 h θ h_\theta hθ共同构成了我们方法的第一阶段,只需执行一次。
3.2.2 计算视觉相似度
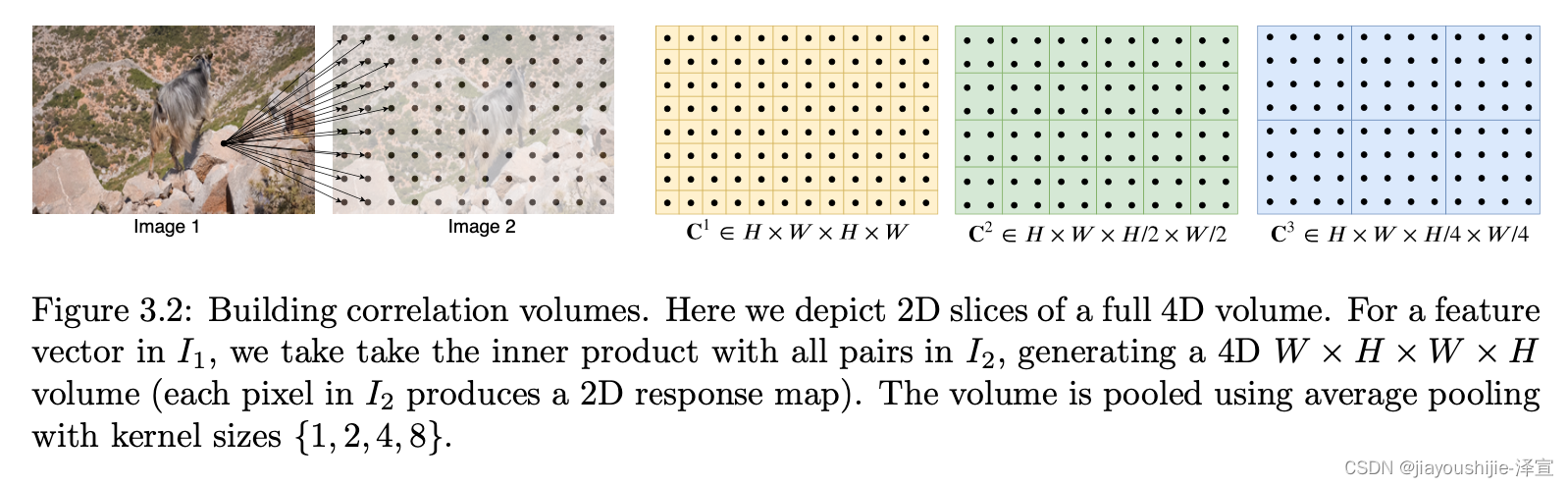
我们通过构建所有对之间的完整相关体来计算视觉相似度。给定图像特征 g θ ( I 1 ) ∈ R H × W × D g_\theta(I_1)\in\mathbb{R}^{H\times W\times D} gθ(I1)∈RH×W×D和 g θ ( I 2 ) ∈ R H × W × D g_\theta(I_2)\in\mathbb{R}^{H\times W\times D} gθ(I2)∈RH×W×D,相关体通过取所有特征向量对之间的点积形成。相关体 C C C可以高效地计算为单个矩阵乘法。
C ( g θ ( I 1 ) , g θ ( I 2 ) ) ∈ R H × W × H × W , C i j k l = ∑ h g θ ( I 1 ) i j h ⋅ g θ ( I 2 ) k l h (3.1) C(g_\theta(I_1),g_\theta(I_2))\in\mathbb{R}^{H\times W\times H\times W},\quad C_{ijkl}=\sum_h g_\theta(I_1){ijh}\cdot g\theta(I_2)_{klh} \tag{3.1} C(gθ(I1),gθ(I2))∈RH×W×H×W,Cijkl=h∑gθ(I1)ijh⋅gθ(I2)klh(3.1)
相关金字塔: 我们通过对相关体的最后两个维度进行池化来构建一个4层金字塔 { C 1 , C 2 , C 3 , C 4 } \{C_1,C_2,C_3,C_4\} {C1,C2,C3,C4},核大小为1,2,4和8,步长等价(图3.2)。因此,体积 C k C_k Ck的维度为 H × W × H / 2 k × W / 2 k H \times W \times H/2^k \times W/2^k H×W×H/2k×W/2k。这组体积给出了关于大位移和小位移的信息;然而,通过保持前2个维度( I 1 I_1 I1维度),我们保持了高分辨率信息,使我们的方法能够恢复小的快速移动物体的运动。
相关查找: 我们定义了一个查找算子 L C \mathcal{L}_C LC,通过从相关金字塔索引来生成特征图。给定光流 ( f 1 , f 2 ) (f_1,f_2) (f1,f2)的当前估计,我们将 I 1 I_1 I1中的每个像素 x = ( u , v ) x=(u,v) x=(u,v)映射到其在 I 2 I_2 I2中的估计对应点: x ′ = ( u + f 1 ( u ) , v + f 2 ( v ) ) x'=(u+f_1(u),v+f_2(v)) x′=(u+f1(u),v+f2(v))。然后我们定义 x ′ x' x′周围的局部网格
N ( x ′ ) r = { x ′ + d x ∣ d x ∈ Z 2 , ∥ d x ∥ 1 ≤ r } (3.2) \mathcal{N}(x')_r=\{x'+dx\mid dx\in\mathbb{Z}^2,\|dx\|_1\leq r\} \tag{3.2} N(x′)r={x′+dx∣dx∈Z2,∥dx∥1≤r}(3.2)
作为使用L1距离在 x ′ x' x′的 r r r单位半径内的整数偏移集合。我们使用局部邻域 N ( x ′ ) r \mathcal{N}(x')_r N(x′)r从相关体索引。由于 N ( x ′ ) r \mathcal{N}(x')_r N(x′)r是实数网格,我们使用双线性采样。
我们对金字塔的所有级别执行查找,使得级别 k k k的相关体 C k C_k Ck使用网格 N ( x ′ / 2 k ) r \mathcal{N}(x'/2^k)_r N(x′/2k)r索引。各级之间的常数半径意味着较低级别的较大上下文:对于最低级别 k = 4 k=4 k=4,使用半径4对应于原始分辨率下256像素的范围。然后将每个级别的值concatenate成单个特征图。
高分辨率图像的高效计算: all-pairs相关的计算复杂度为 O ( N 2 ) \mathcal{O}(N^2) O(N2),其中 N N N是像素数,但只需计算一次,在迭代次数 M M M中为常数。然而,存在一个等价的实现,利用内积和平均池化的线性性,其复杂度为 O ( N M ) \mathcal{O}(NM) O(NM)。考虑级别 m m m的代价体 C i j k l m C_{ijkl}^m Cijklm和特征图 g ( 1 ) = g θ ( I 1 ) , g ( 2 ) = g θ ( I 2 ) g^{(1)}=g_\theta(I_1),g^{(2)}=g_\theta(I_2) g(1)=gθ(I1),g(2)=gθ(I2):
C i j k l m = 1 2 2 m ∑ p 2 m ∑ q 2 m ⟨ g i , j ( 1 ) , g 2 m k + p , 2 m l + q ( 2 ) ⟩ = ⟨ g i , j ( 1 ) , 1 2 2 m ( ∑ p 2 m ∑ q 2 m g 2 m k + p , 2 m l + q ( 2 ) ) ⟩ C_{ijkl}^m=\frac{1}{2^{2m}}\sum_{p}^{2^m}\sum_{q}^{2^m}\langle g_{i,j}^{(1)},g_{2^mk+p,2^ml+q}^{(2)}\rangle=\langle g_{i,j}^{(1)},\frac{1}{2^{2m}}(\sum_{p}^{2^m}\sum_{q}^{2^m}g_{2^mk+p,2^ml+q}^{(2)})\rangle Cijklm=22m1p∑2mq∑2m⟨gi,j(1),g2mk+p,2ml+q(2)⟩=⟨gi,j(1),22m1(p∑2mq∑2mg2mk+p,2ml+q(2))⟩
这是 2 m × 2 m 2^m\times 2^m 2m×2m网格中相关响应的平均值。这意味着 C i j k l m C_{ijkl}^m Cijklm的值可以计算为特征向量 g θ ( I 1 ) i j g_\theta(I_1){ij} gθ(I1)ij和 g θ ( I 2 ) g\theta(I_2) gθ(I2)在 2 m × 2 m 2^m\times 2^m 2m×2m核大小下池化的内积。在这个替代实现中,我们不预先计算相关,而是预先计算池化的图像特征图。在每次迭代中,我们按需计算每个相关值------只在查找时计算。这给出了 O ( N M ) \mathcal{O}(NM) O(NM)的复杂度。我们通过经验发现,由于GPU上高度优化的矩阵例程,预先计算所有对很容易实现且不是瓶颈------即使对于1088x1920的视频,它也只占总推理时间的17%。请注意,如果它成为瓶颈,我们总是可以切换到替代实现。
3.2.3 迭代更新
我们的更新算子从初始点 f 0 = 0 f_0=0 f0=0估计一系列流估计 { f 1 , ... , f N } \{f_1,\dots,f_N\} {f1,...,fN}。在每次迭代中,它产生一个更新方向 δ f \delta f δf,应用于当前估计: f k + 1 = δ f + f k f_{k+1}=\delta f+f_k fk+1=δf+fk。
更新算子将流、相关和潜在隐状态作为输入,并输出更新 δ f \delta f δf和更新的隐状态。我们的更新算子的架构旨在模仿优化算法的步骤。因此,我们在深度上使用绑定权重,并使用有界激活来鼓励收敛到不动点。更新算子被训练为执行更新,使得序列收敛到不动点 f k → f ∗ f_k\rightarrow f^* fk→f∗。
初始化: 默认情况下,我们将流场初始化为到处为0,但我们的迭代方法使我们能够灵活地尝试替代方案。当应用于视频时,我们测试warm-start初始化,其中上一对帧的光流被前向投影到下一对帧,使用最近邻插值填充遮挡间隙。
输入: 给定当前流估计 f k f_k fk,我们使用它从相关金字塔中检索相关特征,如第3.2.2节所述。相关特征然后由2个卷积层处理。此外,我们对流估计本身应用2个卷积层以生成流特征。最后,我们直接注入来自上下文网络的输入。然后将输入特征图作为相关、流和上下文特征的concatenation。
更新: 更新算子的核心组件是基于GRU单元的门控激活单元,全连接层被卷积替换:
z t = σ ( Conv 3 × 3 ( [ h t − 1 , x t ] , W z ) ) (3.3) z_t=\sigma(\text{Conv}{3\times 3}([h{t-1},x_t],W_z)) \tag{3.3} zt=σ(Conv3×3([ht−1,xt],Wz))(3.3)
r t = σ ( Conv 3 × 3 ( [ h t − 1 , x t ] , W r ) ) (3.4) r_t=\sigma(\text{Conv}{3\times 3}([h{t-1},x_t],W_r)) \tag{3.4} rt=σ(Conv3×3([ht−1,xt],Wr))(3.4)
h ~ t = tanh ( Conv 3 × 3 ( [ r t ⊙ h t − 1 , x t ] , W h ) ) (3.5) \tilde{h}t=\tanh(\text{Conv}{3\times 3}([r_t\odot h_{t-1},x_t],W_h)) \tag{3.5} h~t=tanh(Conv3×3([rt⊙ht−1,xt],Wh))(3.5)
h t = ( 1 − z t ) ⊙ h t − 1 + z t ⊙ h ~ t (3.6) h_t=(1-z_t)\odot h_{t-1}+z_t\odot\tilde{h}_t \tag{3.6} ht=(1−zt)⊙ht−1+zt⊙h~t(3.6)
其中 x t x_t xt是前面定义的流、相关和上下文特征的concatenation。我们还尝试了可分离的ConvGRU单元,其中我们用两个GRU替换 3 × 3 3\times 3 3×3卷积:一个具有 1 × 5 1\times 5 1×5卷积,一个具有 5 × 1 5\times 1 5×1卷积,以在不显著增加模型大小的情况下增加感受野。架构细节在图3.3中提供。
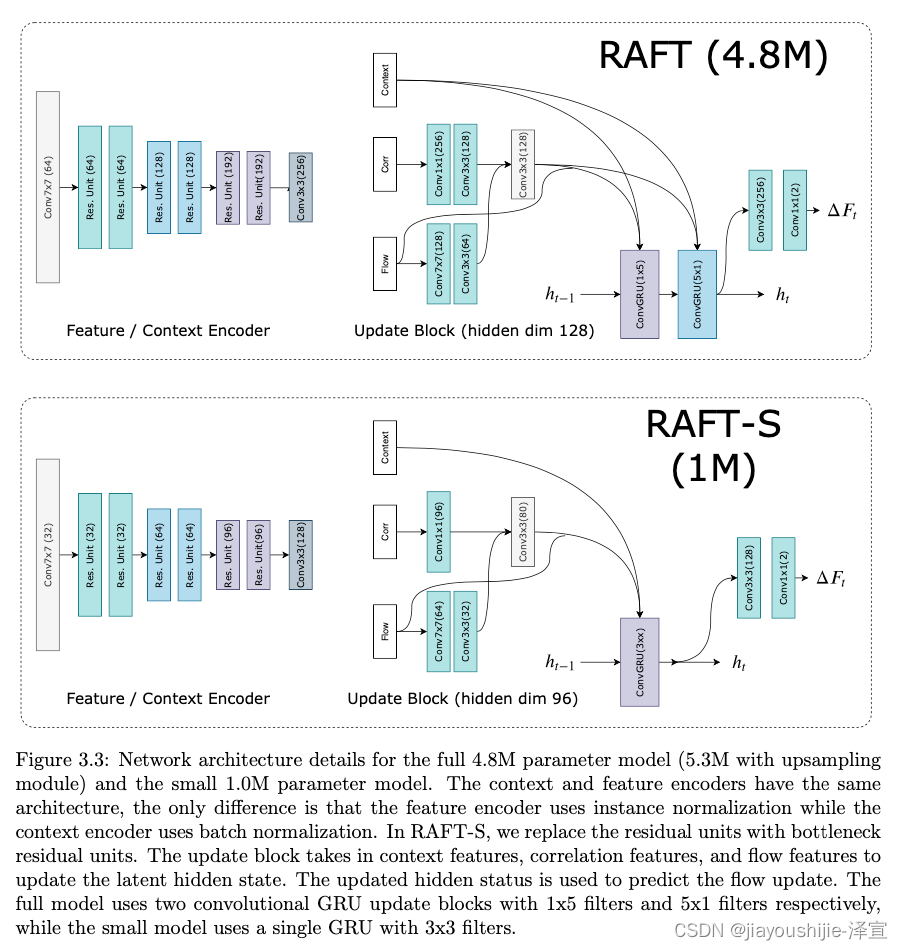
流预测: GRU输出的隐状态通过两个卷积层来预测流更新 δ f \delta f δf。输出流的分辨率是输入图像的1/8。在训练和评估期间,我们将预测的流场上采样到完整分辨率。
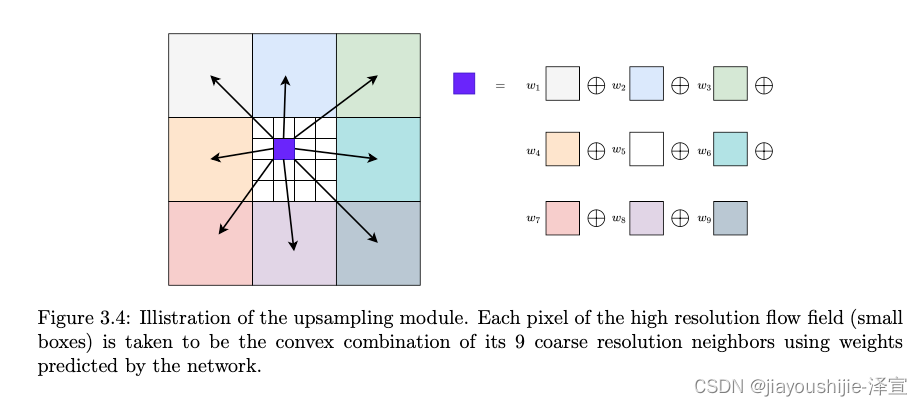
上采样: 网络在1/8分辨率输出光流。我们通过将每个像素的全分辨率流视为其粗分辨率邻居的 3 × 3 3\times 3 3×3网格的凸组合来将光流上采样到全分辨率(图3.4)。我们使用两个卷积层来预测 H / 8 × W / 8 × ( 8 × 8 × 9 ) H/8 \times W/8 \times (8 \times 8 \times 9) H/8×W/8×(8×8×9)的mask,并对9个邻居的权重执行softmax。通过使用mask对邻域进行加权组合,然后进行permute和reshape到 H × W × 2 H \times W \times 2 H×W×2维流场,找到最终的高分辨率流场。这一层可以使用PyTorch中的unfold函数直接实现。
3.2.4 监督
我们在预测流 { f 1 , ... , f N } \{f_1,\dots,f_N\} {f1,...,fN}与真实流之间的 ℓ 1 \ell_1 ℓ1距离上监督我们的网络,权重呈指数增加。给定真实流 f g t f_{gt} fgt,损失定义为
L = ∑ i = 1 N γ N − i ∥ f g t − f i ∥ 1 (3.7) \mathcal{L}=\sum_{i=1}^N\gamma^{N-i}\|f_{gt}-f_i\|_1 \tag{3.7} L=i=1∑NγN−i∥fgt−fi∥1(3.7)
其中我们在实验中设置 γ = 0.8 \gamma=0.8 γ=0.8。
3.3 实验
我们在Sintel[11]和KITTI[18]上评估RAFT。遵循先前的工作,我们在FlyingChairs[15]和FlyingThings[33]上预训练我们的网络,然后进行数据集特定的微调。我们的方法在Sintel(clean和final passes)和KITTI上都达到了最先进的性能。此外,我们在DAVIS数据集[37]的1080p视频上测试了我们的方法,以证明我们的方法可以扩展到非常高分辨率的视频。
实现细节: RAFT在PyTorch[36]中实现。所有模块都是从头开始用随机权重初始化的。在训练期间,我们使用AdamW[30]优化器并将梯度裁剪到 [ − 1 , 1 ] [-1,1] [−1,1]范围内。除非另有说明,我们在Sintel上评估32次流更新,在KITTI上评估24次。对于每次更新 δ f + f k \delta f+f_k δf+fk,我们只通过 δ f \delta f δf分支反向传播梯度,并将 f k f_k fk分支的梯度归零,如[20]所建议。
训练时间表: 我们使用两个2080Ti GPU训练RAFT。我们在FlyingThings上以批量大小12预训练100k次迭代,然后在FlyingThings3D上以批量大小6训练100k次迭代。我们在Sintel上进行另外100k次微调,类似于MaskFlowNet[52]和PWC-Net+[41],结合来自Sintel[11]、KITTI-2015[34]和HD1K[27]的数据。最后,我们使用在Sintel上微调的模型的权重,在KITTI-2015上额外微调50k次迭代。
额外的细节可以在表3.1中找到。为了与先前的工作进行比较,我们还包括仅在Sintel上微调和仅在KITTI上微调时我们模型的结果。
| Stage | Weights | Training Data | Learning Rate | Batch Size (per GPU) | Weight Decay | Crop Size |
|---|---|---|---|---|---|---|
| Chairs | - | C | 4e-4 | 6 | 1e-4 | [368, 496] |
| Things | Chairs | T | 1.2e-4 | 3 | 1e-4 | [400, 720] |
| Sintel | Things | S+T+K+H | 1.2e-4 | 3 | 1e-5 | [368, 768] |
| KITTI | Sintel | K | 1e-4 | 3 | 1e-5 | [288, 960] |
表3.1: 训练时间表的细节。数据集缩写:C:FlyingChairs,T:FlyingThings,S:Sintel,K:KITTI-2015,H:HD1K。在Sintel微调阶段,数据集分布为S(.71),T(.135),K(.135),H(.02)。
光度增强: 我们通过随机扰动亮度、对比度、饱和度和色调来执行光度增强。我们使用Torchvision ColorJitter,亮度0.4,对比度0.4,饱和度0.4,色调0.5/π。在KITTI上,我们将增强程度降低到亮度0.3,对比度0.3,饱和度0.3,色调0.3/π。以0.2的概率独立对每个图像执行颜色增强。
空间增强: 我们通过随机缩放和拉伸图像来执行空间增强。随机缩放的程度取决于数据集。对于FlyingChairs,我们在 2 [ 0.2 , 1.0 ] 2^{[0.2,1.0]} 2[0.2,1.0]范围内执行空间增强,FlyingThings在 2 [ 0.4 , 0.8 ] 2^{[0.4,0.8]} 2[0.4,0.8]范围内,Sintel在 2 [ 0.2 , 0.6 ] 2^{[0.2,0.6]} 2[0.2,0.6]范围内,KITTI在 2 [ 0.2 , 0.4 ] 2^{[0.2,0.4]} 2[0.2,0.4]范围内。空间增强以0.8的概率执行。
遮挡增强: 遵循HSM-Net[48],我们还以0.5的概率随机擦除 I 2 I_2 I2中的矩形区域以模拟遮挡。
3.3.1 Sintel
我们使用FlyingChairs → \rightarrow →FlyingThings时间表训练我们的模型,然后使用train split进行验证在Sintel数据集上进行评估。结果如表3.2和图3.5所示,我们根据用于训练的数据划分结果。C+T表示模型在FlyingChairs©和FlyingThings(T)上训练,而+ft表示模型在Sintel数据上进行了微调。

像PWC-Net+[41]和MaskFlowNet[52]一样,我们在微调时包括来自KITTI和HD1K的数据。我们用不同的种子训练3次,并报告在Sintel(train)的clean pass上具有中值准确度的模型的结果。
| Training Data | Method | Sintel (train) | KITTI-15 (train) | Sintel (test) | KITTI-15 (test) |
|---|---|---|---|---|---|
| Clean | Final | F1-epe | F1-all | ||
| - | FlowFields[7] | - | - | - | - |
| - | FlowFields++[40] | - | - | - | - |
| S | DCFlow[47] | - | - | - | - |
| S | MRFlow[46] | - | - | - | - |
| C+T | HD3[50] | 3.84 | 8.77 | 13.17 | 24.0 |
| C+T | LiteFlowNet[22] | 2.48 | 4.04 | 10.39 | 28.5 |
| C+T | PWC-Net[42] | 2.55 | 3.93 | 10.35 | 33.7 |
| C+T | LiteFlowNet2[23] | 2.24 | 3.78 | 8.97 | 25.9 |
| C+T | VCN[49] | 2.21 | 3.68 | 8.36 | 25.1 |
| C+T | MaskFlowNet[52] | 2.25 | 3.61 | - | 23.1 |
| C+T | FlowNet2[25] | 2.02 | 3.54 | 10.08 | 30.0 |
| C+T | Ours (small) | 2.21 | 3.35 | 7.51 | 26.9 |
| C+T | Ours (2-view) | 1.43 | 2.71 | 5.04 | 17.4 |
| C+T+S/K | FlowNet2 [25] | (1.45) | (2.01) | (2.30) | (6.8) |
| C+T+S/K | HD3 [50] | (1.87) | (1.17) | (1.31) | (4.1) |
| C+T+S/K | IRR-PWC [24] | (1.92) | (2.51) | (1.63) | (5.3) |
| C+T+S/K | ScopeFlow[8] | - | - | - | - |
| C+T+S/K | Ours (2-view) | (0.77) | (1.20) | (0.64) | (1.5) |
| C+T+S+K+H | LiteFlowNet2[23] | (1.30) | (1.62) | (1.47) | (4.8) |
| C+T+S+K+H | PWC-Net+[41] | (1.71) | (2.34) | (1.50) | (5.3) |
| C+T+S+K+H | VCN [49] | (1.66) | (2.24) | (1.16) | (4.1) |
| C+T+S+K+H | MaskFlowNet[52] | - | - | - | - |
| C+T+S+K+H | Ours (2-view) | (0.76) | (1.22) | (0.63) | (1.5) |
| C+T+S+K+H | Ours (warm-start) | (0.77) | (1.27) | - | - |
表3.2: Sintel和KITTI数据集上的结果。我们在FlyingChairs©和FlyingThing(T)上训练后,在Sintel(train)上测试泛化性能,在clean和final pass上都优于所有现有方法。下面两节显示了我们的模型在数据集特定微调后在公共排行榜上的性能。S/K包括在Sintel上微调时仅使用Sintel数据,在KITTI上微调时仅使用KITTI数据的方法。+S+K+H包括在Sintel上微调时结合KITTI、HD1K和Sintel数据的方法。Ours(warm-start)在Sintel的clean和final passes上排名第一,在KITTI上在所有流方法中排名第一。( 1 ^1 1 FlowNet2最初在Sintel的视差分割上报告结果,3.54是在标准数据上评估其模型时的EPE[22]。 2 ^2 2 [23]发现HD1K数据在Sintel微调期间没有显著帮助,并报告了没有它的结果。)
当使用C+T进行训练时,我们的方法优于所有现有方法,尽管使用了显著更短的训练时间表。我们的方法在Sintel(train)clean pass上实现了1.43的平均EPE(端点误差),比FlowNet2低29%的误差。这些结果证明了良好的跨数据集泛化能力。更好泛化的原因之一是我们网络的结构。通过将光流约束为一系列相同更新步骤的乘积,我们迫使网络学习一个模仿一阶下降算法更新的更新算子。这约束了搜索空间,降低了过拟合的风险,并导致更快的训练和更好的泛化。
在Sintel(test)集上评估时,我们在训练集的clean和final passes以及KITTI和HD1K数据上进行微调。我们的方法在Sintel的clean和final passes上都排名第一,在clean pass上比先前工作低0.9个像素(36%),在final pass上低1.2个像素(30%)。我们评估了两个版本的模型,Ours(two-frame)使用零初始化,而Ours(warp-start)通过前向投影前一帧的流估计来初始化流。由于我们的方法在单一分辨率下运行,我们可以初始化流估计以利用过去帧的运动平滑性,这在使用coarse-to-fine模型时不容易做到。
3.3.2 KITTI
我们还在KITTI上评估RAFT,并在表3.2和图3.6中提供结果。我们首先在Chairs©和FlyingThings(T)上训练后,在KITTI-15(train)分割上评估跨数据集泛化能力。我们的方法大大优于先前的工作,将EPE(端点误差)从8.36提高到5.04,这表明我们网络的基本结构有利于泛化。我们的方法在KITTI排行榜上在所有光流方法中排名第一。

3.3.3 消融实验
我们进行了一系列消融实验来显示每个组件的相对重要性。所有消融版本都在FlyingChairs©+FlyingThings(T)上训练。消融的结果如表3.3所示。在表的每一节中,我们单独测试我们方法的特定组件,我们在最终模型中使用的设置用下划线表示。下面我们更详细地描述每个实验。
| Experiment | Method | Sintel (train) | KITTI-15 (train) | Parameters |
|---|---|---|---|---|
| Clean | Final | F1-epe | ||
| Reference Model (bilinear upsampling), Training: 100k© → \rightarrow → 60k(T) | ||||
| Update Op. | ConvGRU | 1.63 | 2.83 | 5.54 |
| Conv | 2.04 | 3.21 | 7.66 | |
| Tying | Tied Weights | 1.63 | 2.83 | 5.54 |
| Untied Weights | 1.96 | 3.20 | 7.64 | |
| Context | Context | 1.63 | 2.83 | 5.54 |
| No Context | 1.93 | 3.06 | 6.25 | |
| Feature Scale | Single-Scale | 1.63 | 2.83 | 5.54 |
| Multi-Scale | 2.08 | 3.12 | 6.91 | |
| Lookup Radius | 0 | 3.41 | 4.53 | 23.6 |
| 1 | 1.80 | 2.99 | 6.27 | |
| 2 | 1.78 | 2.82 | 5.84 | |
| 4 | 1.63 | 2.83 | 5.54 | |
| Correlation Pooling | No | 1.95 | 3.02 | 6.07 |
| Yes | 1.63 | 2.83 | 5.54 | |
| Correlation Range | 32px | 2.91 | 4.48 | 10.4 |
| 64px | 2.06 | 3.16 | 6.24 | |
| 128px | 1.64 | 2.81 | 6.00 | |
| All-Pairs | 1.63 | 2.83 | 5.54 | |
| Features for Refinement | Correlation | 1.63 | 2.83 | 5.54 |
| Warping | 2.27 | 3.73 | 11.83 | |
| Reference Model (convex upsampling), Training: 100k© → \rightarrow → 100k(T) | ||||
| Upsampling | Convex | 1.43 | 2.71 | 5.04 |
| Bilinear | 1.60 | 2.79 | 5.17 | |
| Inference Updates | 1 | 4.04 | 5.45 | 15.30 |
| 3 | 2.14 | 3.52 | 8.98 | |
| 8 | 1.61 | 2.88 | 5.99 | |
| 32 | 1.43 | 2.71 | 5.00 | |
| 100 | 1.41 | 2.72 | 4.95 | |
| 200 | 1.40 | 2.73 | 4.94 |
表3.3: 消融实验。在我们的最终模型中使用的设置用下划线表示。详见第4.3.3节。
更新算子的架构: 我们使用基于GRU单元的门控激活单元。我们尝试用一组3个带ReLU激活的卷积层替换卷积GRU。使用GRU块可以获得更好的性能,可能是因为门控激活使流估计序列更容易收敛。
权重绑定: 默认情况下,我们在更新算子的所有实例上绑定权重。在这里,我们测试了一个版本,其中每个更新算子学习一组单独的权重。当权重绑定时准确性更好,参数数量显著降低。
上下文: 我们通过训练一个移除上下文网络的模型来测试上下文的重要性。没有上下文,我们仍然获得了很好的结果,优于Sintel和KITTI上的所有现有工作。但上下文是有帮助的。直接将图像特征注入更新算子可能允许在运动边界内更好地聚合空间信息。
特征尺度: 默认情况下,我们在单一分辨率提取特征。我们还尝试通过在每个尺度上单独构建相关体来提取多分辨率特征。单分辨率特征简化了网络架构,并允许在大位移下进行细粒度匹配。
查找半径: 查找半径指定查找操作中使用的网格维度。当使用0半径时,相关体在单个点检索。令人惊讶的是,即使半径为0,我们仍然可以得到粗略的流估计,这意味着网络正在学习使用0阶信息。然而,随着半径的增加,我们看到更好的结果。
相关池化: 我们在单一分辨率输出特征,然后执行池化以生成多尺度体。在这里,我们测试移除池化时的影响。有池化时结果更好,因为大位移和小位移都被捕获。
相关范围: 除了all-pairs相关,我们还尝试仅为每个像素周围的局部邻域构建相关体。我们尝试32像素、64像素和128像素的范围。总的来说,当使用all-pairs时我们得到最好的结果,尽管128px范围足以在Sintel上表现良好,因为大多数位移都在这个范围内。也就是说,all-pairs仍然更可取,因为它消除了指定范围的需要。它也更方便实现:它可以使用矩阵乘法计算,允许我们的方法完全在PyTorch中实现。
用于细化的特征: 我们通过在所有像素对之间构建相关体来计算视觉相似度。在这个实验中,我们尝试用warping层替换相关体,该层使用当前光流估计将特征从 I 2 I_2 I2warp到 I 1 I_1 I1,然后估计残差位移。虽然warping在Sintel上仍然与先前的工作具有竞争力,但相关性能明显更好,特别是在KITTI上。
上采样: RAFT在1/8分辨率输出流场。我们比较双线性上采样与我们学习的上采样模块。上采样模块产生更好的结果,特别是在运动边界附近。我们在图3.7中显示了上采样层的定性影响。

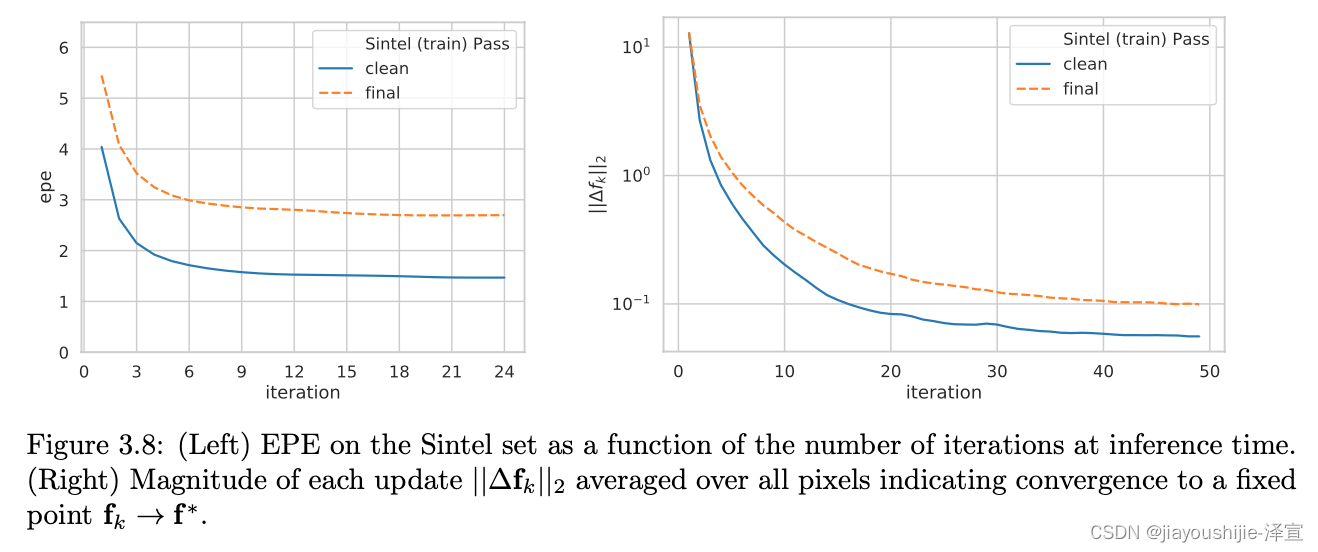
推理更新: 尽管我们在训练期间展开12次更新,但我们可以在推理期间应用任意次数的更新。在表3.3中,我们提供了选定更新次数的数值结果,并测试200次的极端情况以显示我们的方法不会发散。我们的方法快速收敛,在3次更新后超过PWC-Net,在6次更新后超过FlowNet2,但随着更多更新而继续改进。收敛图如图3.8所示。
3.3.4 时间和参数数量
推理时间和参数数量如图3.9所示。准确性由在FlyingChairs和FlyingThings(C+T)上训练后在Sintel(train)final pass上的性能决定。在这些图中,我们在10次迭代后报告准确性和时间,并使用GTX 1080Ti GPU为我们的方法计时。其他方法的参数数量取自其论文,我们在我们的硬件上运行时报告时间。RAFT在参数数量、推理时间和训练迭代次数方面更有效。Ours-S仅使用1M参数,但优于超过6倍大的PWC-Net和VCN。我们在表3.4中提供了参数、时间和训练迭代的数值表。
| Method | Parameters (M) | Time (Reported) | Time (1080Ti) | Training Iter. (#GPUs) | Accuracy |
|---|---|---|---|---|---|
| LiteFlowNetX[22] | 0.9M | 0.03s | - | 2000k | 4.79 |
| LiteFlowNet[22] | 5.4M | 0.09s | 0.09s | 2000k | 4.04 |
| IRR-PWC[24] | 6.4M | - | 0.20s | 850k | 3.95 |
| PWCNet+[41] | 9.4M | 0.03s | 0.04s | 1700k | 3.93 |
| VCN[49] | 6.2M | 0.18s | 0.26s | 220k(4) | 3.63 |
| FlowNet2[25] | 162M | 0.12s | 0.11s | 7000k | 3.54 |
| Ours (small) | 1.0M | - | 0.05s | 160k(2) | 3.37 |
| Ours (mixed) | 5.3M | - | 0.10s | 240k(1) | 2.85 |
| Ours | 5.3M | - | 0.10s | 200k(2) | 2.83 |
表3.4: Sintel(train)final pass上的参数数量、推理时间、训练迭代次数和准确性。我们使用GTX 1080Ti GPU在10次更新后报告我们方法的时间和准确性。如果可能,我们下载其他方法的代码并使用我们的机器重新计时。如果使用多个GPU训练模型,我们在括号中报告用于训练的GPU数量。我们还可以使用混合精度训练Ours(mixed)并获得类似的结果,同时仅在单个GPU上训练。总的来说,与先前的工作相比,RAFT需要更少的训练迭代和参数。
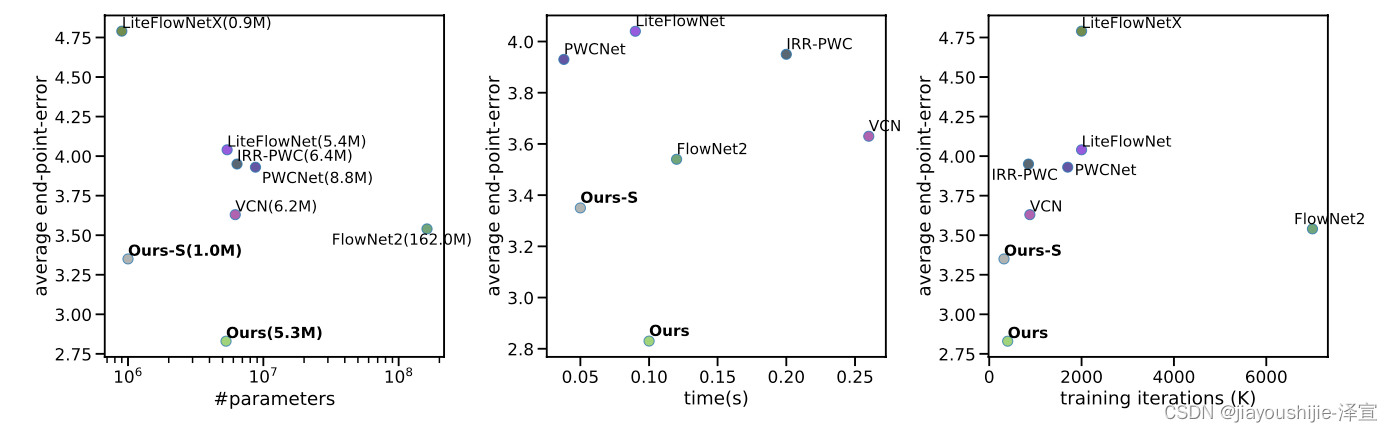
图3.9: 参数数量、推理时间和训练迭代次数与准确性的比较图。准确性由在C+T上训练后在Sintel(train)final pass上的EPE衡量。左:与其他方法相比的参数数量与准确性。RAFT的参数效率更高,同时实现更低的EPE。中:使用我们的硬件计时的推理时间与准确性。右:训练迭代次数与准确性(取迭代次数和使用的GPU数量的乘积)。
3.3.5 非常高分辨率的视频
为了证明我们的方法可以很好地扩展到非常高分辨率的视频,我们将我们的网络应用于DAVIS[37]数据集的HD视频。我们使用1080p(1088x1920)分辨率的视频,并应用我们方法的12次迭代。在1080p视频上,12次迭代的推理时间为550ms,all-pairs相关需要95ms。图3.10可视化了DAVIS上的示例结果。

图3.10: DAVIS上1080p(1088x1920)视频的结果(每帧550ms)。
3.4 结论
我们提出了RAFT------循环all-pairs场变换------一种新的端到端可训练的光流深度网络模型。RAFT的独特之处在于它使用大量轻量级的循环更新算子在单一分辨率下运行。我们的方法在各种数据集上实现了最先进的准确性,具有很强的跨数据集泛化能力,并在推理时间、参数数量和训练迭代次数方面都很高效。
1\] Jonas Adler and Ozan ¨Oktem. Solving ill-posed inverse problems using iterative deep neural networks. Inverse Problems, 33(12):124007, 2017. \[2\] Jonas Adler and Ozan ¨Oktem. Learned primal-dual reconstruction. IEEE transactions on medical imaging, 37(6):1322--1332, 2018. \[3\] Akshay Agrawal, Brandon Amos, Shane Barratt, Stephen Boyd, Steven Diamond, and J Zico Kolter. Di↵erentiable convex optimization layers. In Advances in Neural Information Processing Systems, pages 9558--9570, 2019. \[4\] Brandon Amos and J Zico Kolter. Optnet: Di↵erentiable optimization as a layer in neural networks. In Proceedings of the 34th International Conference on Machine Learning-Volume 70, pages 136--145. JMLR. org, 2017. \[5\] Shaojie Bai, J Zico Kolter, and Vladlen Koltun. Trellis networks for sequence modeling. arXiv preprint arXiv:1810.06682, 2018. \[6\] Shaojie Bai, J Zico Kolter, and Vladlen Koltun. Deep equilibrium models. In Advances in Neural Information Processing Systems, pages 688--699, 2019. \[7\] Christian Bailer, Bertram Taetz, and Didier Stricker. Flow fields: Dense correspondence fields for highly accurate large displacement optical flow estimation. In Proceedings of the IEEE international conference on computer vision, pages 4015--4023, 2015. \[8\] Aviram Bar-Haim and Lior Wolf. Scopeflow: Dynamic scene scoping for optical flow. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 7998--8007, 2020. \[9\] Michael J Black and Padmanabhan Anandan. A framework for the robust estimation of optical flow. In 1993 (4th) International Conference on Computer Vision, pages 231--236. IEEE, 1993. \[10\] Thomas Brox, Christoph Bregler, and Jitendra Malik. Large displacement optical flow. In 2009 IEEE Conference on Computer Vision and Pattern Recognition, pages 41--48. IEEE, 2009. \[11\] Daniel J Butler, Jonas Wul↵, Garrett B Stanley, and Michael J Black. A naturalistic open source movie for optical flow evaluation. In European conference on computer vision, pages 611--625. Springer, 2012. \[12\] Antonin Chambolle and Thomas Pock. A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of mathematical imaging and vision, 40(1):120--145, 2011. \[13\] Qifeng Chen and Vladlen Koltun. Full flow: Optical flow estimation by global optimization over regular grids. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 4706--4714, 2016. \[14\] Kyunghyun Cho, Bart Van Merri¨enboer, Dzmitry Bahdanau, and Yoshua Bengio. On the properties of neural machine translation: Encoder-decoder approaches. arXiv preprint arXiv:1409.1259, 2014. \[15\] Alexey Dosovitskiy, Philipp Fischer, Eddy Ilg, Philip Hausser, Caner Hazirbas, Vladimir Golkov, Patrick Van Der Smagt, Daniel Cremers, and Thomas Brox. Flownet: Learning optical flow with convolutional networks. In Proceedings of the IEEE international conference on computer vision, pages 2758--2766, 2015. \[16\] Lijie Fan, Wenbing Huang, Chuang Gan, Stefano Ermon, Boqing Gong, and Junzhou Huang. End-to-end learning of motion representation for video understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 6016--6025, 2018. \[17\] John Flynn, Michael Broxton, Paul Debevec, Matthew DuVall, Graham Fy↵e, Ryan Styles Overbeck, Noah Snavely, and Richard Tucker. Deepview: High-quality view synthesis by learned gradient descent. 2019. \[18\] Andreas Geiger, Philip Lenz, Christoph Stiller, and Raquel Urtasun. Vision meets robotics: The kitti dataset. The International Journal of Robotics Research, 32(11):1231--1237, 2013. \[19\] Heiko Hirschmuller. Stereo processing by semiglobal matching and mutual information. IEEE Transactions on pattern analysis and machine intelligence, 30(2):328--341, 2007. \[20\] Markus Hofinger, Samuel Rota Bul\`o, Lorenzo Porzi, Arno Knapitsch, and Peter Kontschieder. Improving optical flow on a pyramidal level. In ECCV, 2020. \[21\] Berthold KP Horn and Brian G Schunck. Determining optical flow. In Techniques and Applications of Image Understanding, volume 281, pages 319--331. International Society for Optics and Photonics, 1981. \[22\] Tak-Wai Hui, Xiaoou Tang, and Chen Change Loy. Liteflownet: A lightweight convolutional neural network for optical flow estimation. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 8981--8989, 2018. \[23\] Tak-Wai Hui, Xiaoou Tang, and Chen Change Loy. A lightweight optical flow cnn--revisiting data fidelity and regularization. arXiv preprint arXiv:1903.07414, 2019. \[24\] Junhwa Hur and Stefan Roth. Iterative residual refinement for joint optical flow and occlusion estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5754--5763, 2019. \[25\] Eddy Ilg, Nikolaus Mayer, Tonmoy Saikia, Margret Keuper, Alexey Dosovitskiy, and Thomas Brox. Flownet 2.0: Evolution of optical flow estimation with deep networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 2462--2470, 2017. \[26\] Erich Kobler, Teresa Klatzer, Kerstin Hammernik, and Thomas Pock. Variational networks: connecting variational methods and deep learning. In German conference on pattern recognition, pages 281--293. Springer, 2017. \[27\] Daniel Kondermann, Rahul Nair, Katrin Honauer, Karsten Krispin, Jonas Andrulis, Alexander Brock, Burkhard Gussefeld, Mohsen Rahimimoghaddam, Sabine Hofmann, Claus Brenner, et al. The hci benchmark suite: Stereo and flow ground truth with uncertainties for urban autonomous driving. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, pages 19--28, 2016. \[28\] Xia Li, Jianlong Wu, Zhouchen Lin, Hong Liu, and Hongbin Zha. Recurrent squeeze-and-excitation context aggregation net for single image deraining. In Proceedings of the European Conference on Computer Vision (ECCV), pages 254--269, 2018. \[29\] Zhengfa Liang, Yiliu Feng, Yulan Guo, Hengzhu Liu, Wei Chen, Linbo Qiao, Li Zhou, and Jianfeng Zhang. Learning for disparity estimation through feature constancy. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2811--2820, 2018. \[30\] Ilya Loshchilov and Frank Hutter. Decoupled weight decay regularization. arXiv preprint arXiv:1711.05101, 2017. \[31\] Yao Lu, Jack Valmadre, Heng Wang, Juho Kannala, Mehrtash Harandi, and Philip Torr. Devon: Deformable volume network for learning optical flow. In The IEEE Winter Conference on Applications of Computer Vision, pages 2705--2713, 2020. \[32\] Zhaoyang Lv, Frank Dellaert, James M Rehg, and Andreas Geiger. Taking a deeper look at the inverse compositional algorithm. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4581--4590, 2019. \[33\] Nikolaus Mayer, Eddy Ilg, Philip Hausser, Philipp Fischer, Daniel Cremers, Alexey Dosovitskiy, and Thomas Brox. A large dataset to train convolutional networks for disparity, optical flow, and scene flow estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4040--4048, 2016. \[34\] Moritz Menze and Andreas Geiger. Object scene flow for autonomous vehicles. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 3061--3070, 2015. \[35\] Moritz Menze, Christian Heipke, and Andreas Geiger. Discrete optimization for optical flow. In German Conference on Pattern Recognition, pages 16--28. Springer, 2015. \[36\] Adam Paszke, Sam Gross, Soumith Chintala, Gregory Chanan, Edward Yang, Zachary DeVito, Zeming Lin, Alban Desmaison, Luca Antiga, and Adam Lerer. Automatic di↵erentiation in pytorch. 2017. \[37\] Jordi Pont-Tuset, Federico Perazzi, Sergi Caelles, Pablo Arbel´aez, Alex Sorkine-Hornung, and Luc Van Gool. The 2017 davis challenge on video object segmentation. arXiv preprint arXiv:1704.00675, 2017. \[38\] Ren´e Ranftl, Kristian Bredies, and Thomas Pock. Non-local total generalized variation for optical flow estimation. In European Conference on Computer Vision, pages 439--454. Springer, 2014. \[39\] Anurag Ranjan and Michael J Black. Optical flow estimation using a spatial pyramid network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4161--4170, 2017. \[40\] Ren´e Schuster, Christian Bailer, Oliver Wasenm¨uller, and Didier Stricker. Flowfields++: Accurate optical flow correspondences meet robust interpolation. In 2018 25th IEEE International Conference on Image Processing (ICIP), pages 1463--1467. IEEE, 2018. \[41\] Deqing Sun, Xiaodong Yang, Ming-Yu Liu, and Jan Kautz. Models matter, so does training: An empirical study of cnns for optical flow estimation. arXiv preprint arXiv:1809.05571, 2018. \[42\] Deqing Sun, Xiaodong Yang, Ming-Yu Liu, and Jan Kautz. Pwc-net: Cnns for optical flow using pyramid, warping, and cost volume. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 8934--8943, 2018. \[43\] Chengzhou Tang and Ping Tan. Ba-net: Dense bundle adjustment network. arXiv preprint arXiv:1806.04807, 2018. \[44\] Zachary Teed and Jia Deng. Deepv2d: Video to depth with di↵erentiable structure from motion. arXiv preprint arXiv:1812.04605, 2018. \[45\] Philippe Weinzaepfel, Jerome Revaud, Zaid Harchaoui, and Cordelia Schmid. Deepflow: Large displacement optical flow with deep matching. In Proceedings of the IEEE international conference on computer vision, pages 1385--1392, 2013. \[46\] Jonas Wul↵, Laura Sevilla-Lara, and Michael J Black. Optical flow in mostly rigid scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4671--4680, 2017. \[47\] Jia Xu, Ren´e Ranftl, and Vladlen Koltun. Accurate optical flow via direct cost volume processing. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 1289--1297, 2017. \[48\] Gengshan Yang, Joshua Manela, Michael Happold, and Deva Ramanan. Hierarchical deep stereo matching on high-resolution images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5515--5524, 2019. \[49\] Gengshan Yang and Deva Ramanan. Volumetric correspondence networks for optical flow. In Advances in Neural Information Processing Systems, pages 793--803, 2019. \[50\] Zhichao Yin, Trevor Darrell, and Fisher Yu. Hierarchical discrete distribution decomposition for match density estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 6044--6053, 2019. \[51\] Christopher Zach, Thomas Pock, and Horst Bischof. A duality based approach for realtime tv-l1 optical flow. In Joint pattern recognition symposium, pages 214--223. Springer, 2007. \[52\] Shengyu Zhao, Yilun Sheng, Yue Dong, Eric I Chang, Yan Xu, et al. Maskflownet: Asymmetric feature matching with learnable occlusion mask. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 6278--6287, 2020. \[53\] Huizhong Zhou, Benjamin Ummenhofer, and Thomas Brox. Deeptam: Deep tracking and mapping. In Proceedings of the European conference on computer vision (ECCV), pages 822--838, 2018.