基于变分模态分解和Cramer von Mises检验的一维信号降噪方法（MATLAB）

关于变分模态分解：

变分模态分解中为什么要各个模态估计的带宽之和最小？

因为VMD是个优化问题，VMD方法首先在时域构造一个共同优化的目标，该目标在所有成分完全重构原信号的约束下追求所有成分的带宽总和最小（窄带假设）。实际上，该共同优化目标被转换到频域内通过交替乘子法ADMM求解。在频域上，该方法可以看作是对原信号中所有成分频谱系数和中心频率的共同搜索。

如何更好地对变分模态分解进行优化？

结合分数阶傅里叶变换方法。基于分数阶傅里叶变换方法FRFT对线性调频LFM信号参数估计的优点，利用FRFT估计各个模态分量的中心频率，并在信号保真项中增加关于中心频率的约束，从而提高模态分量的分解精度。

变分模态分解是如何被提出的？

受同步压缩小波变换SST中的同步分析和经验小波变换EWT中频域搜索思路，Dragomiretskiy大佬提出了变分模态分解VMD。VMD方法首先在时域构造一个共同优化的目标，该目标在所有成分完全重构原信号的约束下追求所有成分的带宽总和最小（窄带假设）。实际上，该共同优化目标被转换到频域内通过交替乘子法ADMM求解。在频域上，该方法可以看作是对原信号中所有成分频谱系数和中心频率的共同搜索。

VMD由于其频域内严格的窄带约束，共同优化以及傅里叶逆变换的使用，其分解成分具有更加细致的频率分辨，并且分解出的模态分量更类似于调幅载波正弦的形态。这进一步使得 VMD 具有更高的噪声鲁棒性，对中心频率的估计也比EWT 更加准确。

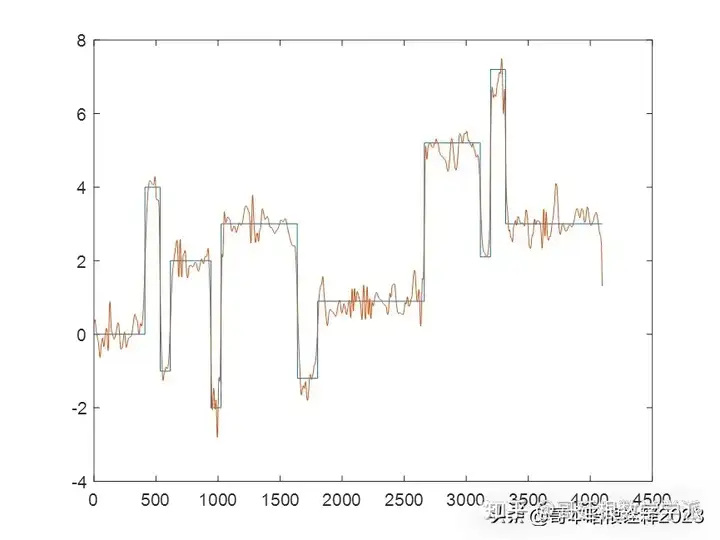
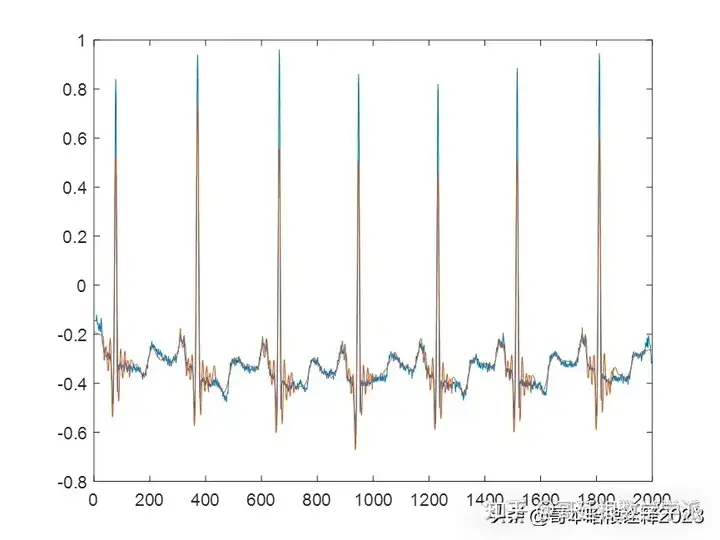
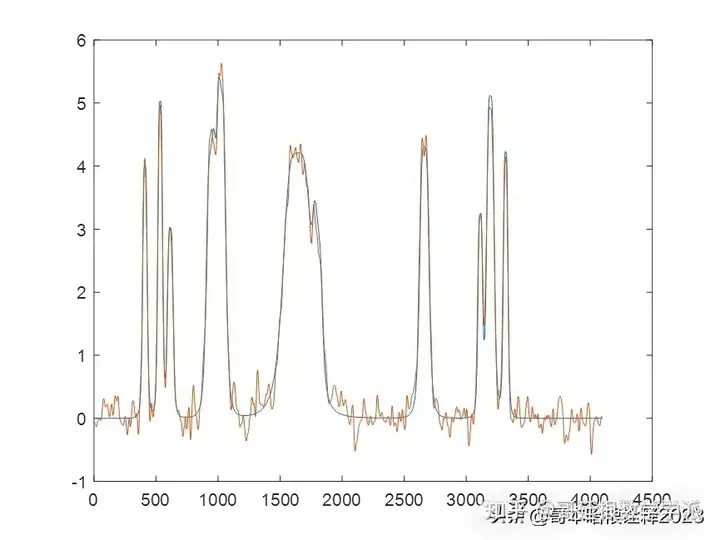
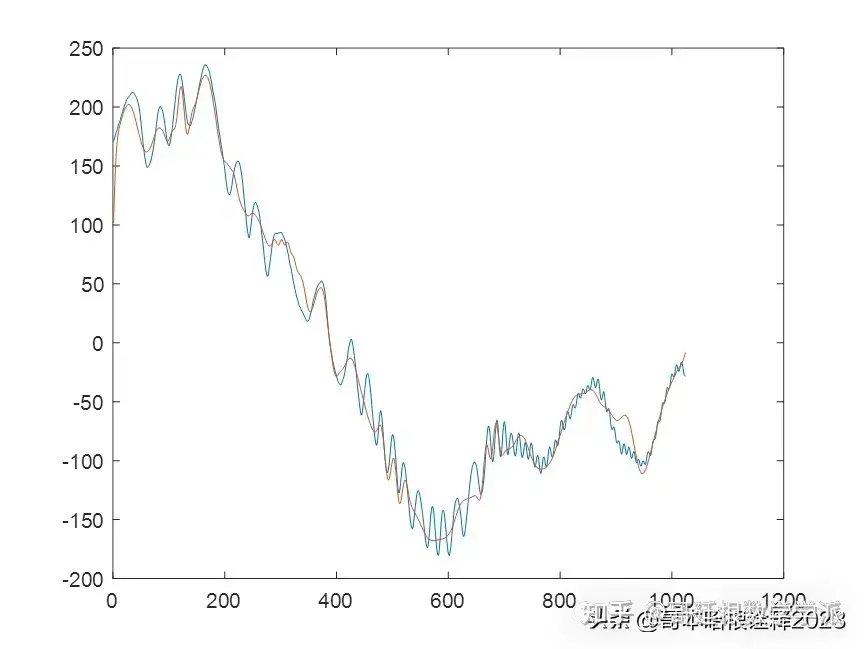
鉴于此，采用变分模态分解和Cramer von Mises检验对一维时间序列信号进行降噪处理，运行环境为MATLAB R2018A。

% some sample parameters for VMD
alpha = 2000;        % moderate bandwidth constraint
tau = 0;            % noise-tolerance (no strict fidelity enforcement)
DC = 0;             % no DC part imposed
init = 1;           % initialize omegas uniformly
tol = 1e-7;


[imf1, imf_hat, omega] = VMD(f, alpha, tau, NIMF, DC, init, tol);
imf=imf1/sigma;
if size(imf,1)<NIMF
    NIMF=size(imf,1)-1;
    warning('NIMF found to be less than the size of actual imf');
end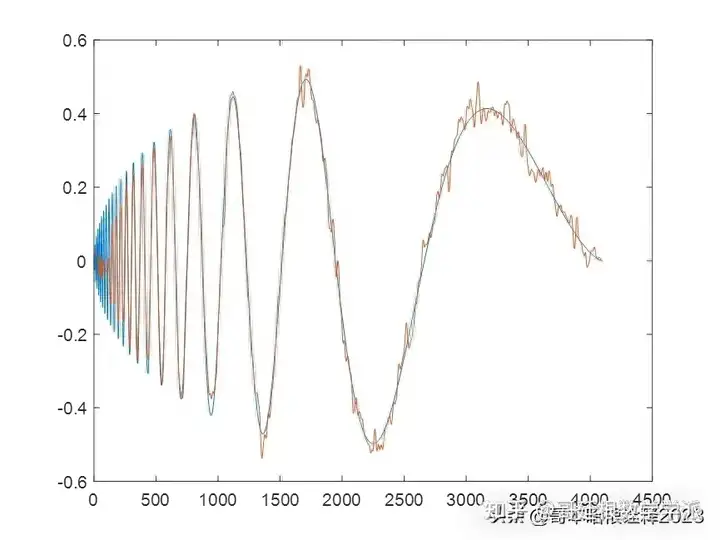

完整数据和代码通过知乎学术咨询获得：
https://www.zhihu.com/consult/people/792359672131756032?isMe=1

擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。