算法：BFS 解决多源最短路问题

多源最短路

题目一：矩阵

题目二：飞地的数量

题目三：地图中的最高点

题目四：地图分析

多源最短路

首先想要知道多源最短路，就先要明白单源最短路，bfs解决单源最短路问题前面学习过，单源最短路就是只有一个起点，到终点的最短路径

多源最短路就是有若干个起点，到终点的最短路径

多源bfs就是使用bfs解决多源最短路问题

这里再强调一下，能够使用bfs，前提必须是边权为1的问题

多源最短路问题的解决方法：

解法一：暴力枚举

将每一个起点都进行bfs，每个起点都会获得一个结果，得到的这些结果中最小的那一个就是题目所要求的

这种解答大概率是会超时的，所以学习下面的解法二

解法二：把所有的源点当成一个源点

此时问题就变为了单一的单源最短路问题了

在单源最短路问题中，我们是把一个起点加入队列，再一层一层往外扩展

而多源最短路问题中，我们是把所有起点加入队列，再一层一层往外扩展

其实代码都是差不多的，区别就是刚开始的队列加入的起点数目不同

题目一：01矩阵

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

复制代码

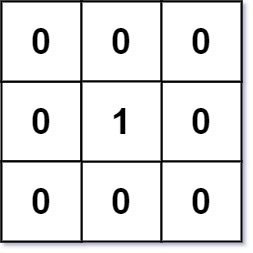
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

复制代码

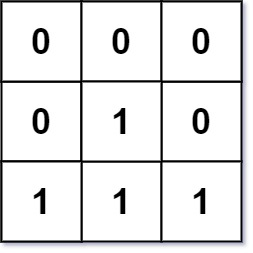
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

这道题的题意就是求矩阵中每一个位置的元素的值，每个位置的值是距离最近的0的距离，如果本身就是0，那么距离就是0

解法一：每个位置挨个求

在这种解法中，二维数组的每一个位置依次求离最近的0的距离，很显然是会超时的，所以这种解法就排除了

解法二：多源BFS + 正难则反

因为采用的多源bfs的策略，最初的想法就是将所有的1当做一个起点，去找0，得到最小的距离，但是当找到0后，我们无法得知当前的找到的最短距离是哪个位置的1，所以这种策略是不对的

那么正难则反，我们可以将所有的0当做一个起点，去找1，这样找到的结果和上面也是一样的

那么此时当找到1后，就可以将当前的最短步数直接更新到1的位置上即可，

所以分为下面两步：

1、把所有的0加入到队列中

遍历过程中，所有0位置的数据可以直接更新为0，因为自己本身就是0，距离也就是0

2、一层一层向外扩展

扩展过程中需要注意，已经赋过值的位置就不需要重复赋值了，因为第一次赋值的一定是最短的距离

细节问题：

在前面的单源最短路问题中，我们使用了三个元素来解决，分别是：

记录是否重复出现的bool数组vis

每一次出队列的个数sz

记录扩展了step层，这里的step就是最短路径了

而多源最短路问题，不需要上面的三个元素，只需要一个dist数组即可

因为初始化时，将dist中的值全部初始化为-1，然后将原始值是0的继续改为0，此时再bfs过程中，只要是-1的才改变它的值，这里就不需要使用vis来标记了

并且我们变化是从(a,b)变为(x,y)，当走到(x,y)后，(x,y)的值就是(a,b)的值+1，所以这里也就不需要之前的sz和step了，直接一个dist数组就能解决，dist数组为-1就表示还没有被搜索过，dist不为-1，就表示当前位置的最短距离

当然了此题也是可以使用这三个全局变量，这里只是说明一下，可以更简便的解题

代码如下：

cpp 复制代码

class Solution 
{
public:
    int dx[4] = {0,0,-1,1};
    int dy[4] = {-1,1,0,0};

    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) 
    {

        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> dist(m, vector<int>(n, -1));
        queue<pair<int, int>> q;
        // 将mat中的0的位置dist该位置也改为0，并将坐标都入队列
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(mat[i][j] == 0)
                {
                    dist[i][j] = 0;
                    q.push({i, j});
                }
            }
        }
        // 一层一层往外扩
        while(!q.empty())
        {
            // 不需要计算sz，因为dist的值就可以表示走了几步
            auto [a, b] = q.front();
            q.pop();
            int tmp = dist[a][b];
            for(int k = 0; k < 4; k++)
            {
                int x = a + dx[k];
                int y = b + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1)
                {
                    dist[x][y] = tmp + 1;
                    q.push({x, y});
                }
            }
        }
        return dist; 
    }
};

题目二：飞地的数量

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次移动是指从一个陆地单元格走到另一个相邻（上、下、左、右 ）的陆地单元格或跨过 grid 的边界。

返回网格中无法在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

复制代码

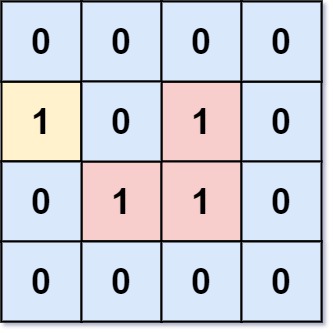
输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

示例 2：

复制代码

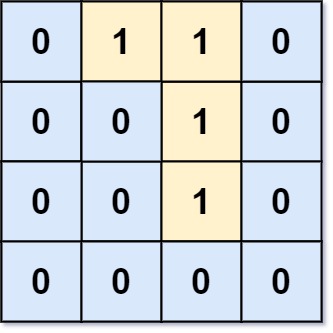
输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

解法一：暴力解法

在遍历的过程中，找到每一个1，每一个1都去判断，是否能够到达边界

这种解法一定会超时，但是也可以做优化

即找到某一个1时，如果发生这个1能够到达边界，那么此时再遍历一遍，将这个遍历过程中的所有1都做一下标记，下次就不需要遍历这些做过标记的1了，这种优化可以做到不超时，但是还是有些麻烦的，因为需要bfs两次，下面看解法二

解法二：正难则反

从里面找1到边界需要考虑的事情非常多，但是我可以从边界的所有1开始向里面搜索，此时搜索到的1就一定是可以到达边界的

这种解法使用bfs时，就可以采用多源bfs的方法，将边界所有的1全部添加进队列中，就可以将所有的满足条件的1全部遍历到，最后再找不满足的条件的1的个数即可

代码如下：

cpp 复制代码

class Solution 
{
public:
    typedef pair<int, int> PII; 
    int dx[4] = {0,0,-1,1};
    int dy[4] = {-1,1,0,0};
    bool vis[501][501];

    int numEnclaves(vector<vector<int>>& g) 
    {
        int m = g.size(), n = g[0].size();
        queue<PII> q;
        // 将边界的1加入队列中
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                if(g[i][j] == 1 && (i == 0 || i == m - 1 || j == 0 || j == n - 1))
                {
                    q.push({i, j});
                    vis[i][j] = true;
                }
        // 多源 bfs
        while(!q.empty())
        {
            auto [a, b] = q.front();
            q.pop();
            for(int k = 0; k < 4; k++)
            {
                int x = a + dx[k];
                int y = b + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && g[x][y] == 1 && vis[x][y] == false)
                {
                    q.push({x, y});
                    vis[x][y] = true;
                }
            }
        }
        // 统计结果
        int ret = 0;
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                if(g[i][j] == 1 && vis[i][j] == false)
                    ret++;
        return ret;
    }
};

题目三：地图中的最高点

给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由陆地和水域单元格组成的地图。

如果 isWater[i][j] == 0 ，格子 (i, j) 是一个陆地格子。
如果 isWater[i][j] == 1 ，格子 (i, j) 是一个水域格子。

你需要按照如下规则给每个单元格安排高度：

每个格子的高度都必须是非负的。
如果一个格子是水域，那么它的高度必须为 0 。
任意相邻的格子高度差至多为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）

找到一种安排高度的方案，使得矩阵中的最高高度值最大。

请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法，请返回 任意一个 。

示例 1：

复制代码

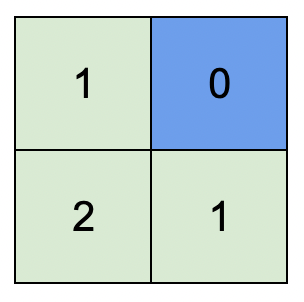
输入：isWater = [[0,1],[0,0]]
输出：[[1,0],[2,1]]
解释：上图展示了给各个格子安排的高度。
蓝色格子是水域格，绿色格子是陆地格。

示例 2：

复制代码

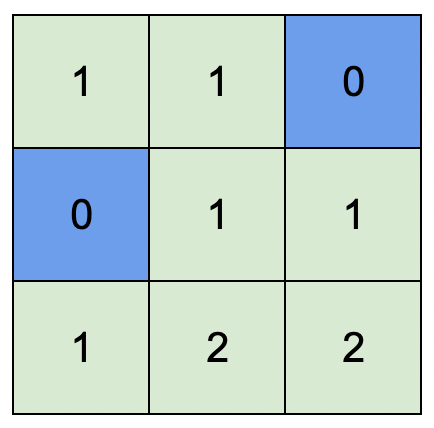
输入：isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出：[[1,1,0],[0,1,1],[1,2,2]]
解释：所有安排方案中，最高可行高度为 2 。
任意安排方案中，只要最高高度为 2 且符合上述规则的，都为可行方案。

这道题的题目描述比较长，其实理解一下就是：

原始矩阵的0表示陆地，1表示水域，需要我们返回一个新矩阵，新矩阵的要求如下：

①原始为水域的位置新矩阵要为0

②其余的位置，每次扩展都可以高度加1

③求整个矩阵的最高高度值

理解完题意，可以看出来，也就是多源bfs，从0位置开始扩展，每次扩展到其他位置时，都+1即可，非常简单

代码如下：

cpp 复制代码

class Solution 
{
public:
    int dx[4] = {0,0,-1,1};
    int dy[4] = {-1,1,0,0};
    typedef pair<int, int> PII;

    vector<vector<int>> highestPeak(vector<vector<int>>& isWater) 
    {
        int m = isWater.size(), n = isWater[0].size();
        vector<vector<int>> height(m, vector<int>(n, -1));
        queue<PII> q;
        // 将所有源点(水域)加入队列
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                if(isWater[i][j] == 1)
                {
                    height[i][j] = 0;
                    q.push({i, j});
                }
        // 多源bfs
        while(!q.empty())
        {
            auto [a, b] = q.front();
            q.pop();
            for(int k = 0; k < 4; k++)
            {
                int x = a + dx[k];
                int y = b + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && height[x][y] == -1)
                {
                    // 每次的高度是之前高度+1
                    height[x][y] = height[a][b] + 1;
                    q.push({x, y});
                }
            }
        }
        return height;
    }
};

题目四：地图分析

你现在手里有一份大小为 n x n 的网格 grid，上面的每个单元格都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

示例 1：

复制代码

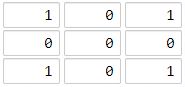
输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

示例 2：

复制代码

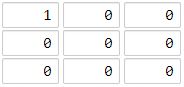
输入：grid = [[1,0,0],[0,0,0],[0,0,0]]
输出：4
解释： 
海洋单元格 (2, 2) 和所有陆地单元格之间的距离都达到最大，最大距离为 4。

同样，此题也非常简单，简单分析一下：

0表示海洋，1表示陆地，请找到海洋距离最远的陆地，如果整个矩阵只有海洋或是陆地，就返回-1

这道题的解法和前面几乎一模一样，找0到1的最大距离，这个并不好找

我们同样正难则反，找1到0的最远距离，每次扩展一层就+1，最后返回最大的值即可

代码如下：

cpp 复制代码

class Solution 
{
public:
    int dx[4] = {0,0,-1,1};
    int dy[4] = {-1,1,0,0};
    typedef pair<int, int> PII;

    int maxDistance(vector<vector<int>>& grid) 
    {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> dist(m, vector<int>(n, -1));
        queue<PII> q;
        for(int i = 0; i < m; i++)
            for(int j = 0; j < n; j++)
                if(grid[i][j] == 1)
                {
                    dist[i][j] = 0;
                    q.push({i, j});
                }
        int ret = -1;
        while(!q.empty())
        {
            auto [a, b] = q.front();
            q.pop();
            for(int k = 0; k < 4; k++)
            {
                int x = a + dx[k];
                int y = b + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1)
                {
                    q.push({x, y});
                    dist[x][y] = dist[a][b] + 1;
                    ret = max(ret, dist[x][y]);
                }
            }
        }
        return ret;
    }
};

BFS 解决多源最短路问题到此结束