一、水体渲染的波形模拟技术-基于物理
基于物理 的波形模拟方法:
- 欧拉方法(Eulerian approaches)[Kass 1990]
- 拉格朗日方法(Lagrangian approaches) [Stam 1995]
- 欧拉-拉格朗日混合方法(Hybrid approaches)[Brien 1995]
预渲染方法:
- 顶点高度位移贴图(Vertex Height Map Displacement) [Yuri 2005]
- 流型图(Flow Map)[Vlachos 2010]
- 离线FFT贴图烘焙(Offline FFT Texture) [Torres 2012]
- 离线流体帧动画烘焙(bake to flipbook)[Bowles 2017]
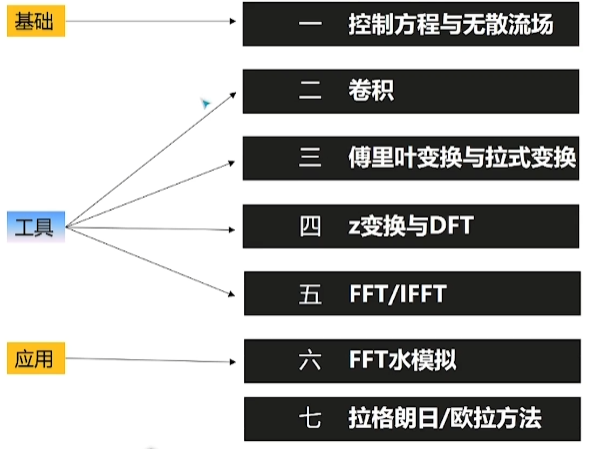
1. 控制方程与无散流场
基于物理的水体模拟方法一般比较昂贵,由于可以离线渲染,所以在电影工业中具有很好的运用。由于现阶段很难用于实时渲染,这边仅进行一个综述性的总结。
基于物理模型的水体模拟方法的核心是对Navier-Stokes方程(Navier-Stokes Equations,NS方程)进行求解。Navier-Stokes方程是一组描述液体和空气之类的流体物质的方程,描述作用于液体任意给定区域的力的动态平衡。除了水体模拟之外,其还可以用于模拟天气,水流,气流,恒星的运动。
Navier-Stokes方程如下:
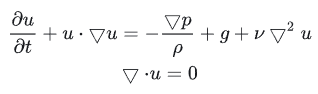
- u 为流体速度矢量(fluid velocity vector)
- p 为流体压力(fluid pressure)
- ρ 为流体密度(fluid density)
- ν 为运动粘度系数(kinematic viscosity coefficient)
- ▽ 为梯度微分(gradient differential)
- ▽2 为拉普拉斯算子(Laplacian operators)
1.1. 流体的描述方法
常用的求解Navier-Stokes方程的方法有欧拉方法(Eularian Method)和拉格朗日方法(Lagrangian Method)两种:
- 欧拉方法(Eularian Method)
-
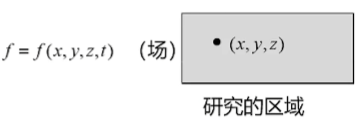
- 是一种基于网格的方法。它从研究流体所占据的空间中各个固定点处的运动着手,分析被运动流体所充满的空间中每一个固定点上流体的速度、压强、密度等参数随时间的变化,以及由某一空间点转到另一空间点时这些参数的变化。
- 看作一个个区域/网格,给出每个时刻每个空间点上的物理量。网格内的数据会变化,形状和位置不会变化。
- 拉格朗日方法(Lagrangian Method)
-
- 是一种基于粒子的方法。它从分析流体各个微粒的运动着手,即研究流体中某一指定微粒的速度、压强、密度等参数随时间的变化,以及研究由一个流体微粒转到其他流体微粒时参数的变化,以此来研究整个流体的运动。最常用的拉格朗日方法是光滑粒子流体力学(Smoothed Particle Hydrodynamics,SPH)方法,其核心渲染思想为流体模拟产生粒子,然后多边形化粒子以产生波。
- 把流体看作一个个粒子,每个粒子做曲线运动。跟踪每个流体质点,记录物理量随时间的变化
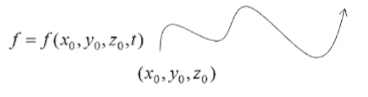


除了独立的两种方法之外,还有结合两者的欧拉-拉格朗日混合方法(Eularian-Lagrangian Hybrid approaches),其主要思想是使用欧拉方法来模拟流体的主体,并使用拉格朗日方法来模拟诸如泡沫,喷雾或气泡之类的细小细节。
FX Guide上有一篇关于电影业界使用流体模拟方法的不错文章,感兴趣的朋友可以了解一下:https://www.fxguide.com/fxfeatured/the-science-of-fluid-sims/
另外,也可以采用bake to flipbook方法,将离线的流体模拟,烘焙成flipbook帧动画,用于实时渲染。
1.2. 控制方程(NS方程)
控制方程是基于欧拉方法的,利用三大守恒定律,将流体看作一块块区域、正方体进行。

对于一小块区域内,满足三大守恒:

增量=流入-流出=m1-m2
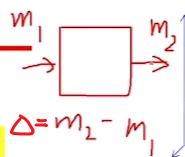


就有下面的式子。

然后再看这张图,对于质量守恒:m=ρV=Δρ*(ΔxΔyΔz)


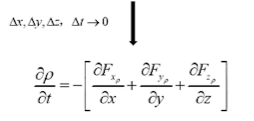
同理动量和内能:

参考前面的:

那么质量、动量和能量的F的计算如下(里面的u就是体积V)(可以只看质量,其他类比):

进而我们将守恒转化为矩阵形式,得到最终的控制方程
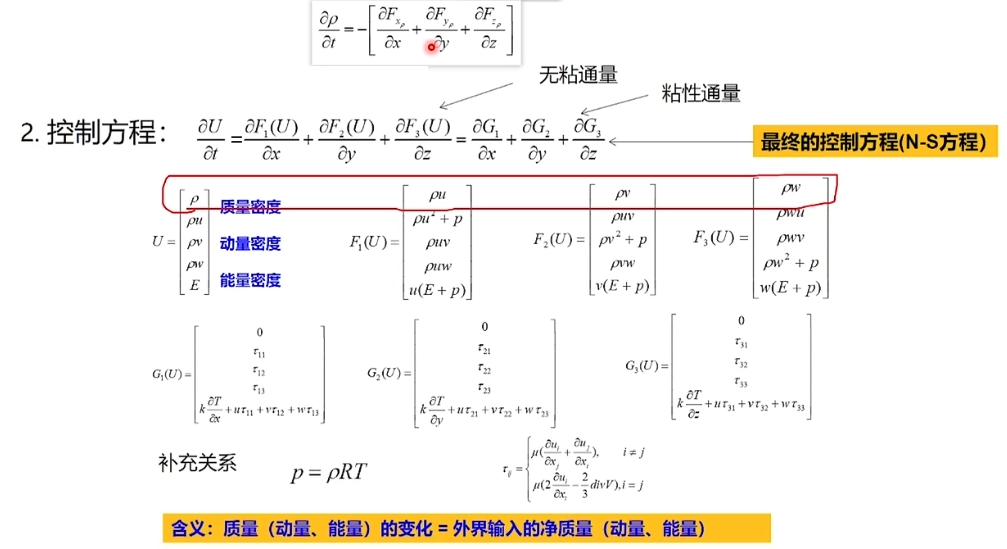
无量纲:例如1m和120cm 将他们的m和cm去掉,化作1/1=1和120/100=1.2或1/0.01=100和120/1=120就叫无量钢化,其中最后选取的参考量m或者cm为就叫特征量,我们可以自己选取特征量。
NS方程的无量纲形式如下,其中带*的就是自己选取的特征量。
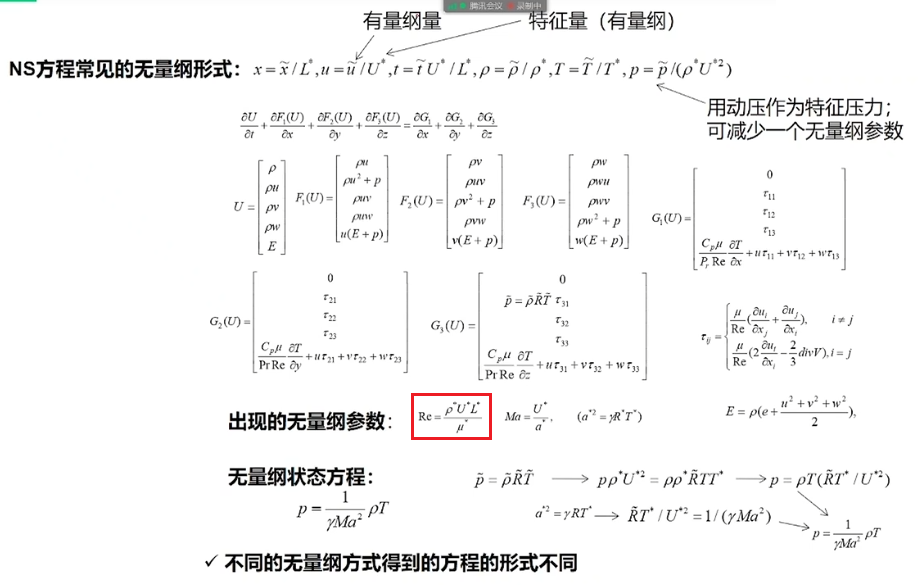
在这里面出现了一个无量纲参数Re,也就是雷诺数。
1.3. 雷诺数Re
我们可以看到雷诺数都是由特征量构成的,因此不同人选取的尺度可能不一样,不一样的尺度也可能导致相同的结果,所以要明确对方的特征量再对比Re。

当层流(流动平缓,各个层不容易交换)时候,Re较小。
当湍流(流动加剧,各个层很容易交换)时候,Re较大层流到湍流的过渡,就是Re增大的过程。
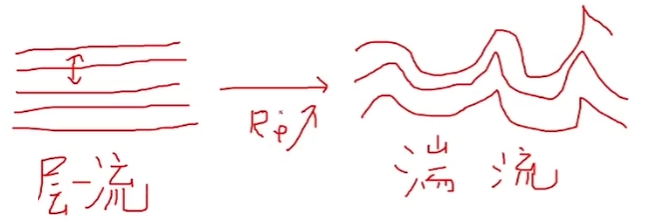
其中卡门涡街就是Re变化导致

其中的黑圆可以看作障碍物,这样当流体流过障碍物时,上下的流速会发生变化,导致流速差,进而导致压强差,对障碍物产生某个方向的力。

1.4. N-S方程的简化(无散流场)
在流体不可压缩情况下

2. 卷积
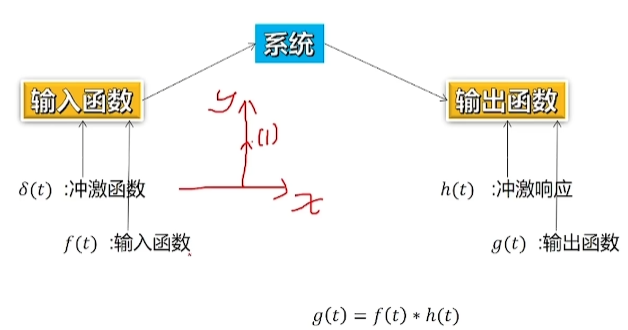
a.系统
系统本身也就相当于一个函数,将一个函数映射到另一个函数
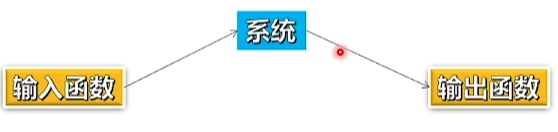
b.阶跃函数和冲激函数

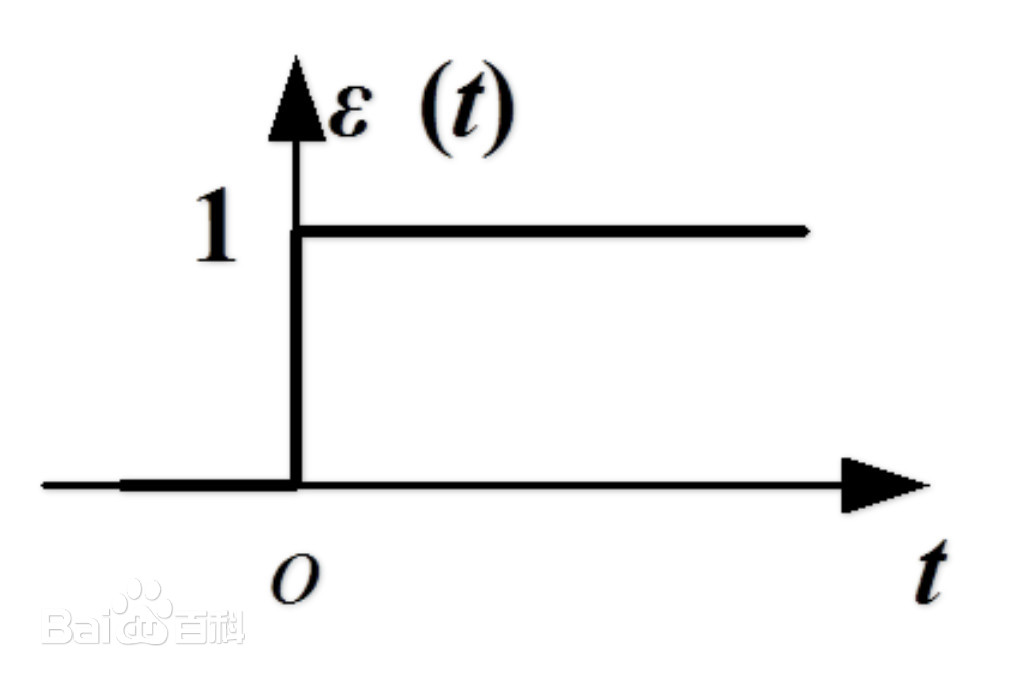
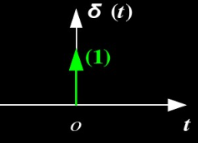
c.冲激响应
当系统的输入函数为冲激函数,那么他输出函数就为冲激响应
d.卷积的作用
将输入函数和冲激响应进行卷积就可以得到输出函数
3. 傅里叶变换与拉氏变换
3.1. 系统的时域分析
3.1.1. 连续系统
输入输出函数就可以用两个微分形式表示
求解系统的表达式=解微分方程
将输入输出函数联立,用一个方程来表示连续系统
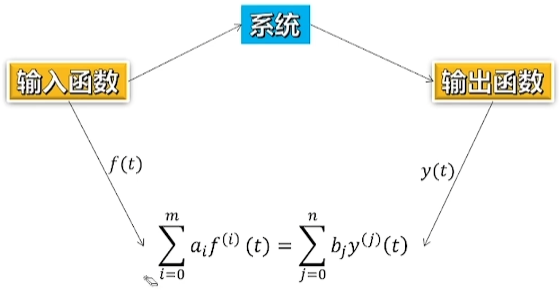
(求i阶导,再乘以对应权重累加):

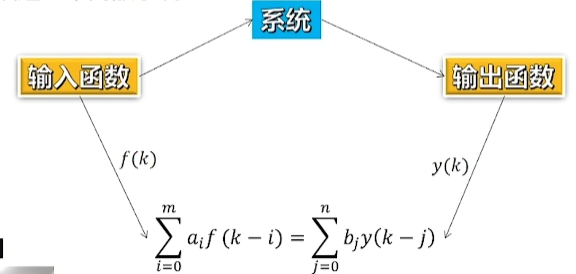
3.1.2. 离散系统
相较于上面就是把微分改为了差分
求解系统表达式=解差分方程
3.2. 连续系统的频域分析
对于一个函数f(t)写成基础函数的求和的形式

其中Fn为下式(T为周期)

当函数为非周期性,就可以认为T趋向无穷大,就可以将有T的地方换为无穷大,就得到了傅里叶变换.
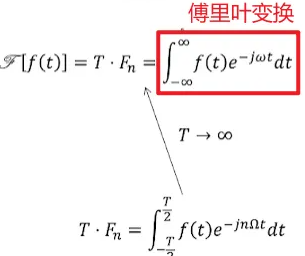
总览:
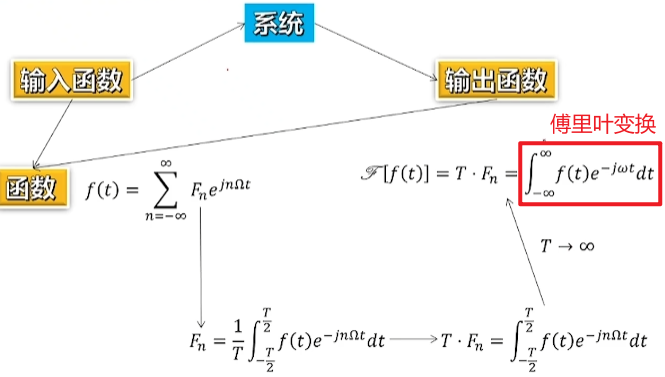
通过傅里叶变换就可以把时域函数f(t)映射到频域函数F(jω)

3.3. 连续系统的s域分析
傅里叶变换有一个局限,当f这个函数在积分下不收敛的时候就没有傅里叶变换,这个时候就可以乘一个收敛因子σ让其收敛,乘完之后的就叫拉式变换
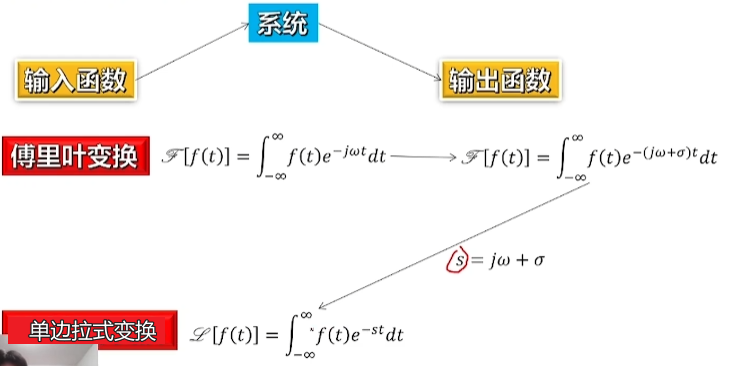
4. Z变换与DFT
4.1. 离散系统的z域分析
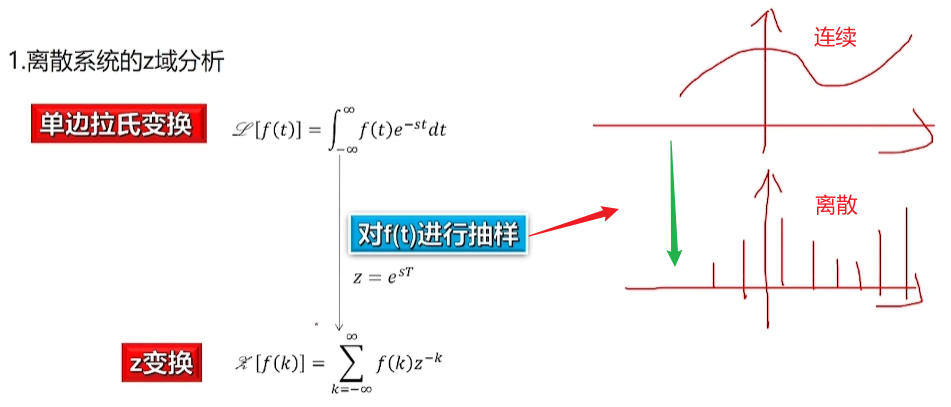
实现了拉氏变换的离散化
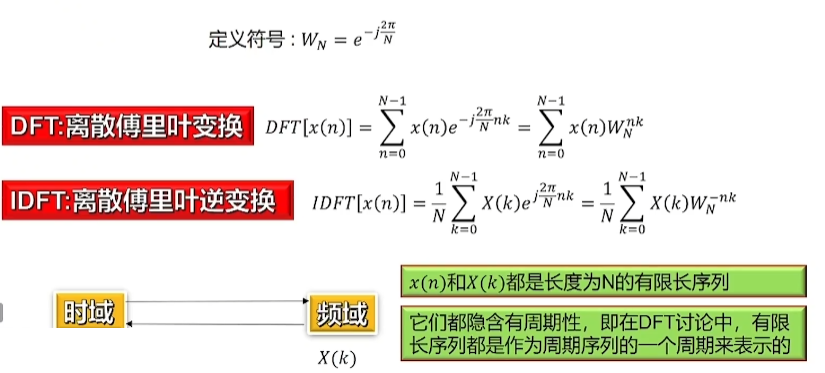
4.2. DFT离散傅里叶变换
傅里叶变化中,如果时域为离散的,那么频域就是周期的。 如果时域为周期的,频域就是离散的。
但计算机只能处理离散数据,所以我们想要把离散的提出来,让他时域和频域都离散
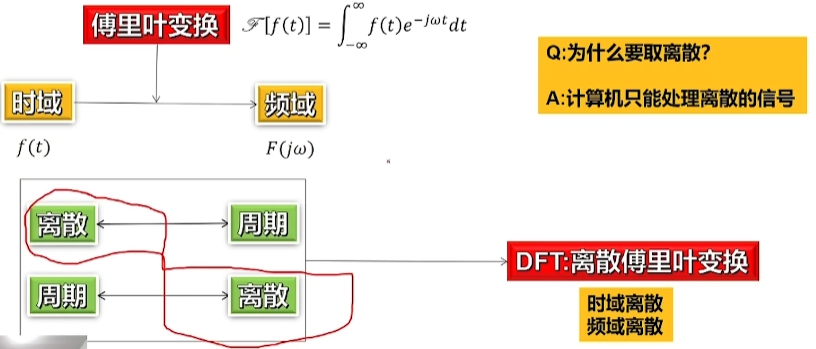
对DFT的任何处理都是先把序列值周期延拓后再作响应处理,然后取主值序列后,处理的结果都隐含周期性,即在DFT讨论中,有限长序列都是作为周期序列的一个周期表示。
Wn是旋转因子,用Wn替换e
x(n)的n是一个周期的分段数
5. FFT ,IFFT
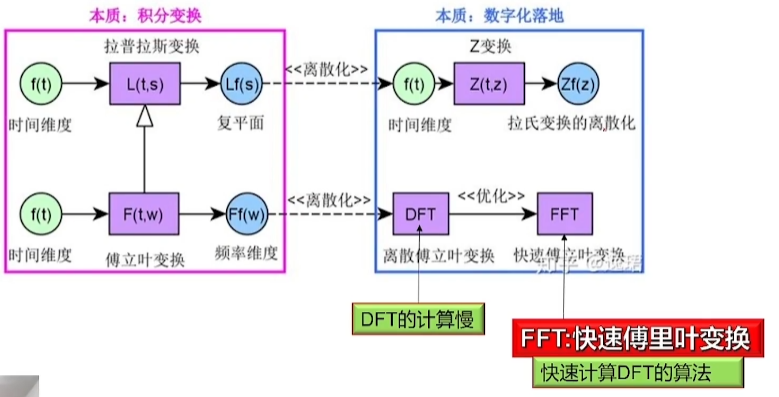
5.1. 快速傅里叶变换 FFT
傅里叶变换(Fourier transform)是一种线性积分变换,用于信号在时域和频域之间的变换。而快速傅里叶变换 (Fast Fourier Transform,FFT), 是一种可在O(nlogn)时间内完成离散傅里叶变换(Discrete Fourier transform,DFT)的高效、快速计算方法集的统称。
FFT的基本思想是把原始的N点序列,依次分解成一系列的短序列。充分利用DFT计算式中指数因子所具有的对称性质和周期性质,进而求出这些短序列相应的DFT并进行适当组合,达到删除重复计算,减少乘法运算和简化结构的目的。
5.2. 改善离散傅里叶变化DFT运算效率的基本途径
利用W的共轭对称性,周期性,可约性,可以将DFT运算中的一些项进行合并,将长序列DFT分解为段系列DFT

快速傅里叶变换算法分两大类DIT和DIF
下面分析按时间抽取(DIT)的基-2FFT算法
5.3. 按时间抽取(DIT)的基-2FFT算法
5.3.1. 算法原理
根据奇偶拆分成两部分,简化计算

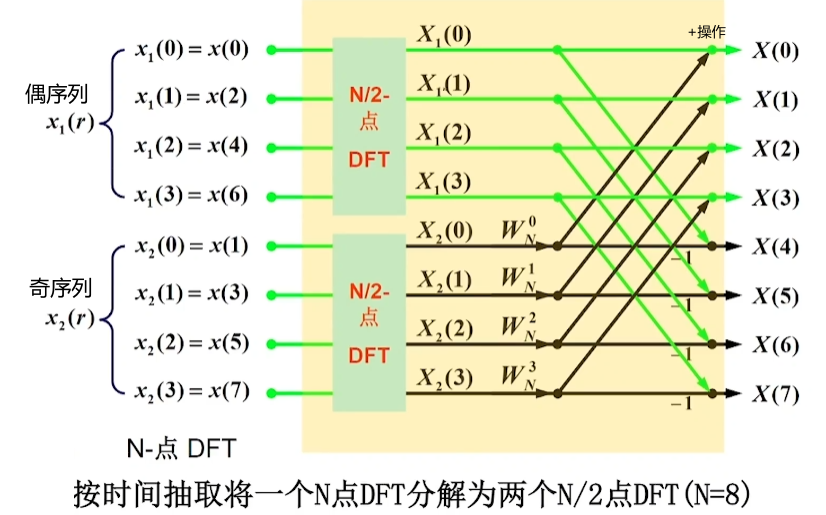
5.3.2. 计算过程
其中X1(k)为偶数,X2(K)为奇数,W为旋转因子,推导过程:


举例,有八个x
如果只有七个x要怎么分?
当不足2的次幂时,就需要补0(对结果没有影响),否则无法使用


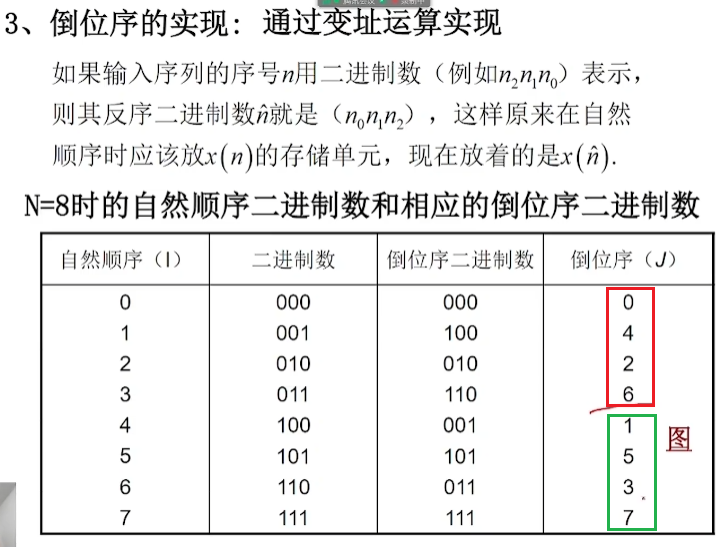
5.3.3. 倒位序
为了分开奇偶,可以使用倒位序的实现:通过变址运算实现。
6. FFT水体渲染
6.1. FFT解泊松方程

求解过程:

6.2. FFT海洋模拟


h(x,t)是波浪的高度(wavehegiht),其中x是位置

7. 拉格朗日/欧拉方法

对于之前式子的求解,我们将其拆为两部分
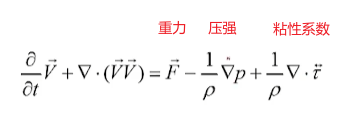
👇
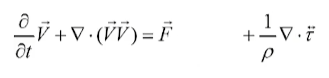
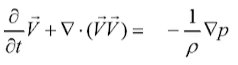
一个流体求解器通常可分为两个步骤:
- 步进(advection):通过速度和加速度更新粒子状态或进行场的流动。
- 投影(projection):根据位置来求得新的速度(去掉速度的散度,维持物质守恒等)。
欧拉网格法在投影(projection)步骤上有较大的优势:
- 易于离散化(discretize)
- 易于实现高效的邻域访问(访问当前像素的周围像素,直接查周围格子)
- 易于设置初始状态
但欧拉网格法在步进(advection)步骤上有一些缺陷:
- 无法精确有效地处理场的流动
- 容易丢失能量和几何细节
而拉格朗日粒子法的优势和缺陷就与此相反:
- 易于更新粒子的运动状态
- 需要复杂的数据结构来实现邻域访问,要把周围的粒子加权求和来做
因此,人们就想到把两种方法结合使用,利用各自的优势同时避免各自的缺陷。
对于我们要解的泊松方程,他的边界条件
例如对于一杯水,他的上边界接触空气压强已知,边界条件叫做Dirichlet condition
他的左右碰到杯壁,压强是未知的,边界条件叫做Neumann condition
二、水体渲染的着色技术

关于水体渲染的Shading部分,首先要提到的是,目前游戏业界的主流方案都不是基于物理的。
首先需要得到水面网格,之后的渲染主要分为基本着色和效果提升两部分

1. LOD
1.1. GeometryClipmaps
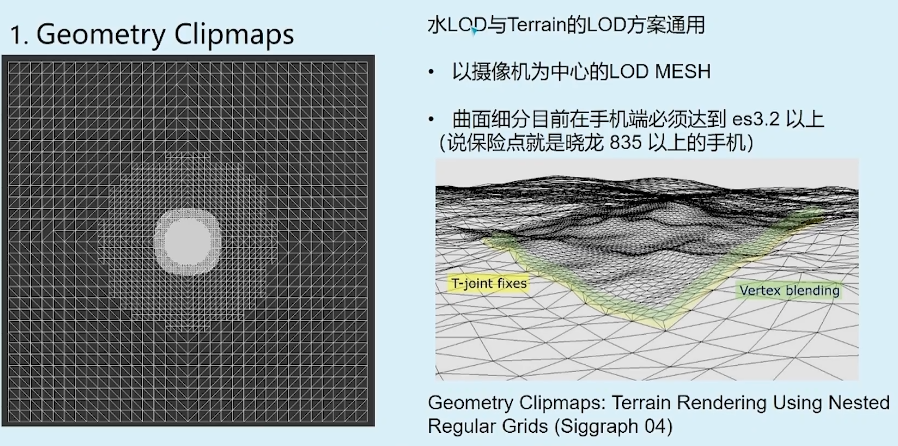
1.2. 渲染性能优化
当水变浅时水的颜色会发生变化,从某些方向看过去可以看到水的分层。为了模拟这种现象我们使用两个LOD的shader:
- LOD0:transparent version,透明,可以看到水底,这部分用完整的shader渲染折射反射之类的,比较耗性能,仅用于较浅的水。
- LOD1:opaque version,这一部分的渲染就当做不透明处理,不进行折射或反射等处理,节约性能,这样就可以在广阔的水域达到一个比较好的效果。

2. 高光
2.1. Minimalist Cook-Torrance
原始Cook-Torrance模型拥有D,F,G项
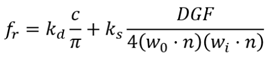
而一个简化版的Cook-Torrance模型:Minimalist Cook-Torrance则有以下项
- 法线分布函数D:normalized Blinn-Phong distribution
- 菲尼尔项F:Schlick approximation
- visibility项V: 是UE中的一个做法,将G项(几何函数)和原始的分母部分进行合并
- 漫反射比例kd:diffuse reflectance
- 镜面反射比例ks:specular reflectance
最终得到的就是
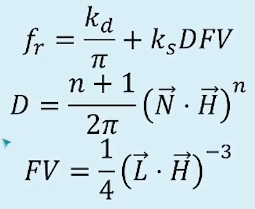
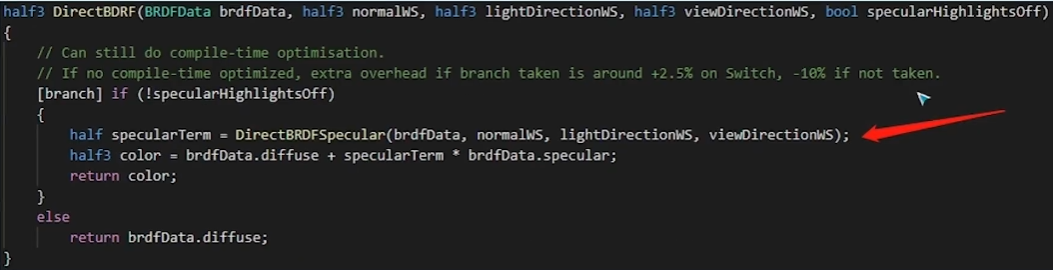
2.2. URP
在URP中想要只输出高光,就可以手动修改InitializeBRDFData各个属性,让其只输出高光和光滑度

这样在之后的DirectBRDF函数中就能保证只输出高光
3. 渲染流程
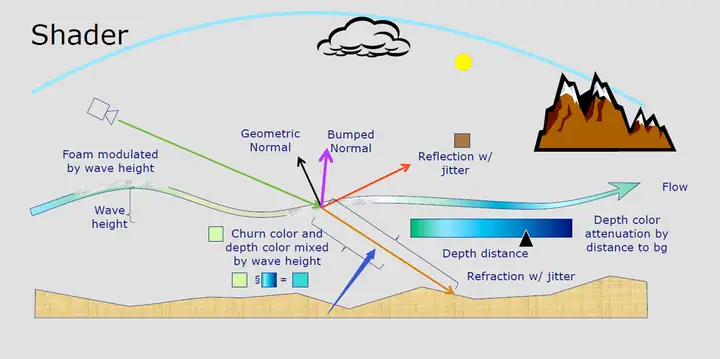
《神秘海域3》在2012年SIGGRAPH上的技术分享中有一张分析水体渲染技术非常经典的图,如下。
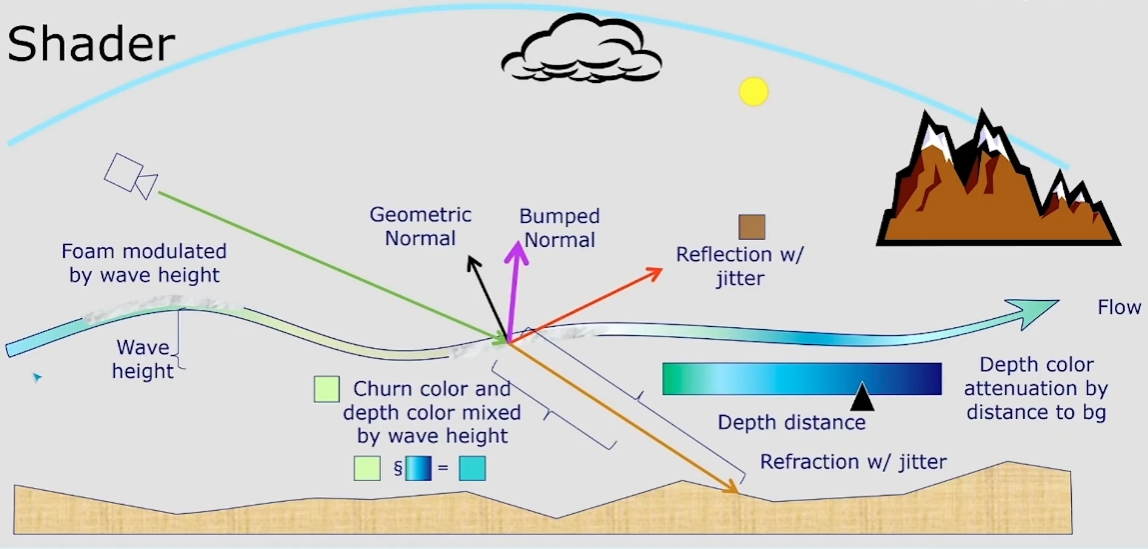
- 白沫由wave height函数计算
- 水的深度颜色:depth distance查找表,随着与背景的距离而衰减
- 扰动:churn颜色和水颜色混合
- 几何法向量,高度法向量,折射
- 使用高度贴图干扰表面法线:除了水体本身的GeometricNormal之外 还需要一个BumpedNormal去扰动表面,增加细节
对此,我们可以将水体渲染的要点总结为:
- 漫反射(Diffuse)
- 镜面反射(Specular)
- 法线贴图(Normal Map)
- 折射(Reflection)
- 通透感(Translucency)
-
- 基于深度的查找表方法(Depth Based LUT Approach)
- 次表面散射(Subsurface Scattering)
- 白沫(Foam/WhiteCap)
- 流动表现(Flow)
- 水下雾效(Underwater Haze)


- 使用被干扰法线的菲涅尔项来混和折射和反射:通过F项(fresnel term)去混合折射refraction和反射reflection,可以在0-1均等采样一个值,当他大于frenelterm时候就让他参与反射,其余就折射。同时水体的折射也取决于水的深度


- 使用扰动来模拟体积效果
- 泡沫是由浪的高度来调节的:主要思路是通过waveHeight,当它离水平面比较远的时候就标记为白沫,然后用白沫贴图混上去,实现浪尖的效果。同时也要根据水面与水底距离产生岸边白沫。
- 折射的颜色去取决于水面和背景的距离
-
- 深度着色可以是线性或者指数函数
- 取泡沫纹理的一个通道来混合深度颜色和扰动颜色(当泡沫移动时,颜色会随着浪花和泡沫而改变)
- 首先有一个根据深度的颜色(线性或指数都行)查找,得到一个水的基本颜色,在此的基础上再添加一个扰动颜色,并且根据waveHeight进行混合mix,达到一种体积效果。当泡沫移动时候,颜色会随着波浪和泡沫滚动而发生变化,所以可以取泡沫纹理的一个通道在深度着色和扰动着色之间混合
- 流动Flow:可以通过向量场(flowmap)来实现滚动法线贴图uv

4. 反射reflection
4.1. 菲涅项
对于反射夹角越小反射越明显,可以使用菲涅项项来做,也可以使用简化的NdotV来做


4.2. 扰动 jitter
反射的扰动可以通过贴图扰动水面的法线来实现。
通过法线贴图的RG通道值对mesh法线x和z进行扰动
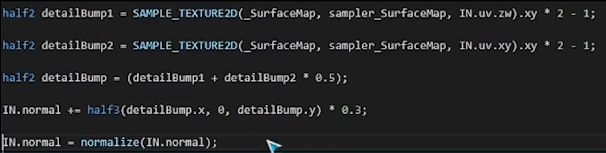

5. 折射refraction和焦散caustic

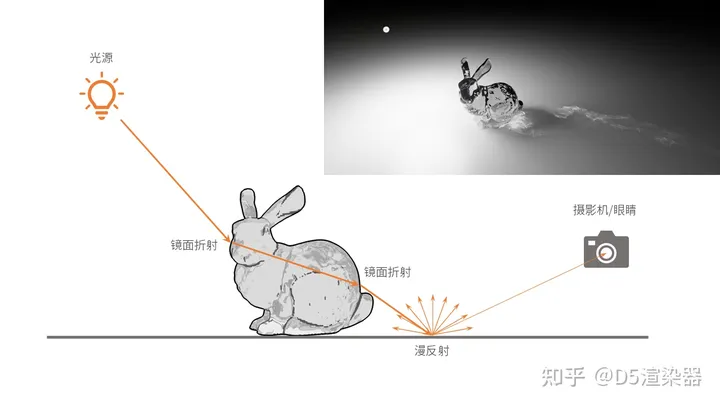
从定义上来说,焦散指的是光从光源--->镜面反射/折射的表面(经过一次或多次反射/折射)--->漫反射表面--->摄影机或眼睛的光照贡献。画成光路分析图是这样:
GPUGens焦散的模拟方案
[GPU Gem] 2. Rendering Water Caustics渲染水体焦散 - 知乎 (zhihu.com)
其中的一个假设为太阳在正上方,这样我们通过n向量通过折射定理计算入射光线v,
再计算v和n向量的的夹角,也就是与太阳夹角得到发射自太阳的密度
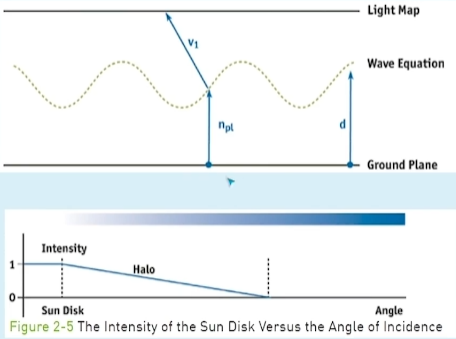
水平是法线与视角方向夹角,竖轴是焦散强度。

Photon Mapping算法学习总结 - 简书 (jianshu.com)
提前了解:

6. 白沫foam
白沫(Foam),在有些文献中也被称为Whitecap,White Water,是一种复杂的现象。即使白沫下方的材质具有其他颜色,白沫也通常看起来是白色的。出现这种现象的原因是因为白沫是由包含空气的流体薄膜组成的。随着每单位体积薄膜的数量增加,所有入射光都被反射而没有任何光穿透到其下方。这种光学现象使泡沫看起来比材质本身更亮,以至于看起来几乎是白色的。

白沫的渲染方案,按大的渲染思路而言,可以分为两类:
- 基于动态纹理(dynamic texture)
- 基于粒子系统(particle system)
按照类型,可以将白沫分为三种:浪尖白沫、岸边白沫、交互白沫。
6.1. 浪尖白沫:基于Saturate高度的方法
第 18 章.使用 Vertex Texture Displacement |NVIDIA 开发人员
《GPU Gems 2》中提出的白沫渲染方案,思路是将一个预先创建的白沫纹理在高于某一高度H0的顶点上进行混合。白沫纹理的透明度根据以下公式进行计算:

- 其中, Hmax 是泡沫最大时的高度, H0 是基准高度, H 是当前高度。
- 白沫纹理可以做成序列帧来表示白沫的产生和消失的演变过程。此动画序列帧既可以由美术师进行制作,也可以采用程序化生成。
- 将上述结果和噪声图进行合理的结合,可以得到更真实的泡沫表现。
6.2. 岸边白沫:基于Multi Ramp Map的方法
《刺客信条3》中的岸边白沫的渲染方案可以总结为:
- 以规则的间距对地形结构进行离线采样,标记出白沫出现的区域。
- 采用高斯模糊和Perlin噪声来丰富泡沫的表现形式,以模拟海岸上泡沫的褪色现象。
- 由于白沫是白色的,因此在R,G和B通道中的每个通道中都放置三张灰度图,然后颜色ramp图将定义三者之间的混合比率,来实现稠密、中等、稀疏三个级别的白沫。要修改白沫表现,美术师只需对ramp图进行颜色校正即可。如下图所示:

- 这样比如取0.1就只有稀疏的白沫,中等和稠密几乎没有
- 当取0.8的时候中等和稀疏完全体现,同时还有部分稠密部分


代码:
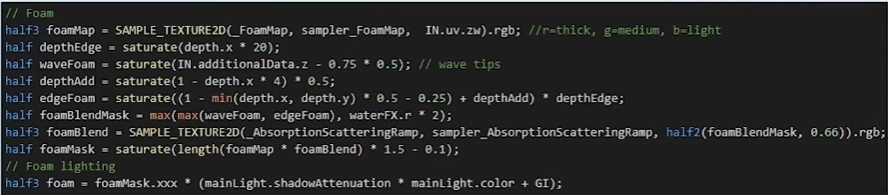
6.3. 交互白沫:基于场景深度的渲染
《盗贼之海(Sea of Thieves)》团队在SIGGRPAPH 2018的talk上也提到了白沫的渲染方案,可以总结如下:
-
放置一个top-down的相机,用于渲染场景深度,通过比较场景深度和水深来得到白沫mask,即:
half4 foamMask = 1 - saturate(_FoamThickness* (depth - i.screenPos.w )) ;
-
最终,将foamMask和基础texture做blend。
-
盗贼之海中,得到相对深度后,还会对白沫mask做渐进模糊(progressively blur),以得到风格化的白沫表现。

图 《盗贼之海(Sea of Thieves)》中的交互白沫

图 《盗贼之海(Sea of Thieves)》中的交互白沫
7. 次表面散射
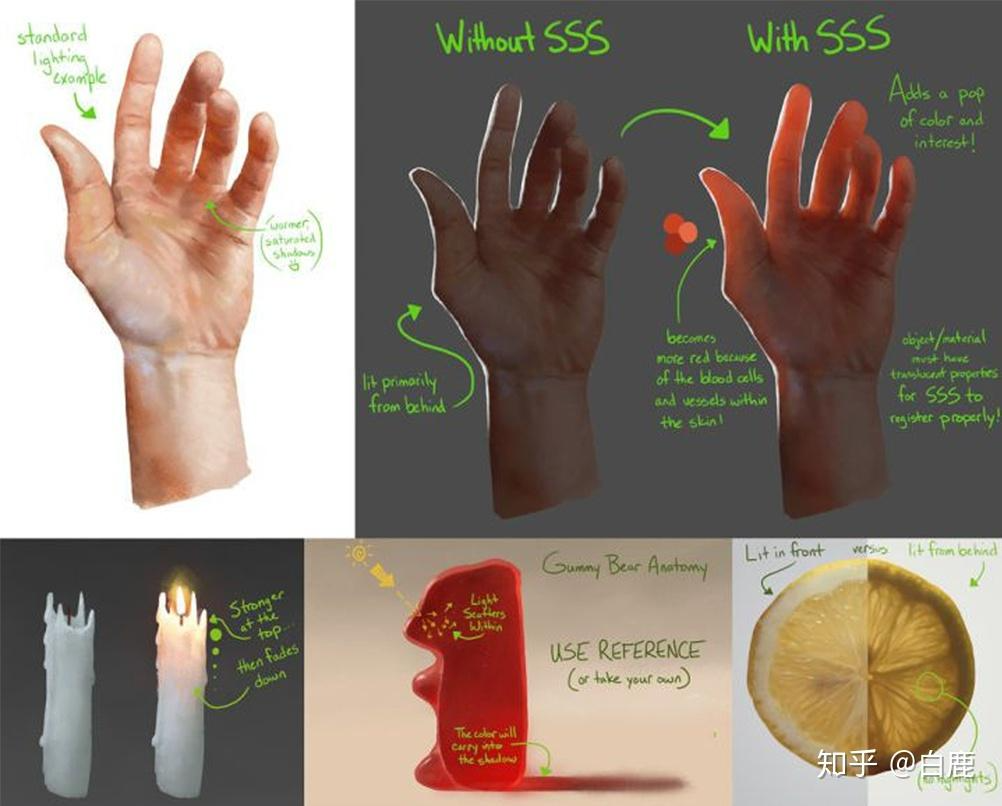
7.1. BSSRDF
描述次表面散射(Subsurface Scattering):BSSRDF 简介 - 知乎 (zhihu.com)
到达水面的光线除了在水体表面发生反射之外,还有部分光线进入水体内部,经过吸收和散射后再次从水体表面射出,即水体的次表面散射现象(Sub-Surface Scattering, SSS)。基于物理的渲染中,求解次表面散射最标准的方法是求解BSSRDF(Bidirectional Surface Scattering Reflectance Distribution Function,双向表面散射反射分布函数)。但在光栅图形学中,求解BSSRDF需要很大的计算量,所以实时渲染业界大多数的水体渲染,依旧是非基于物理的经验型渲染方法。
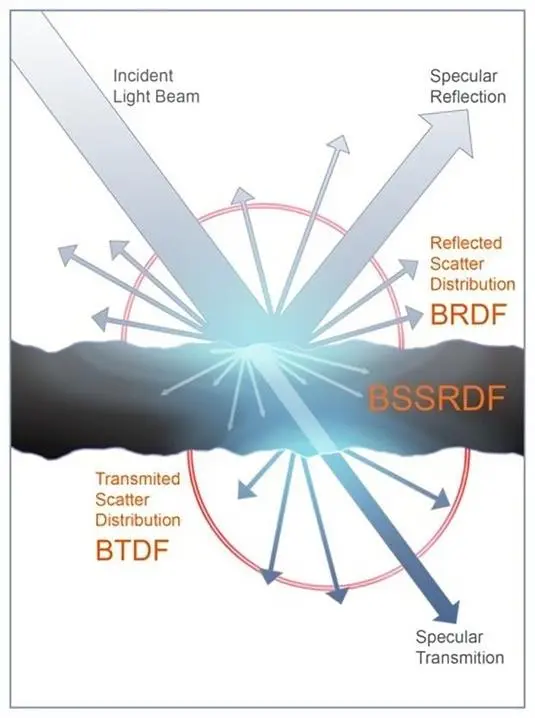

主要分为两部分漫反射项和单次散射项singleScattering ,其中漫反射项由一个反射部分和两个菲涅耳项组成
7.2. 基于深度的查找表方法
Depth Based-LUT方法的思路是,计算视线方向的水体像素深度,然后基于此深度值采样吸收/散射LUT(Absorb/Scatter LUT)纹理,以控制不同深度水体的上色,得到通透的水体质感表现。


其中,视线方向的水体像素深度值计算思路如下图中的蓝色箭头所示的橘褐色区间:
7.3. 快速次表面 Fast SSS
GDC 2011\]上,Frostbite引擎提出的Fast Approximating Subsurface Scattering方案,也可以用于水体渲染的模拟。  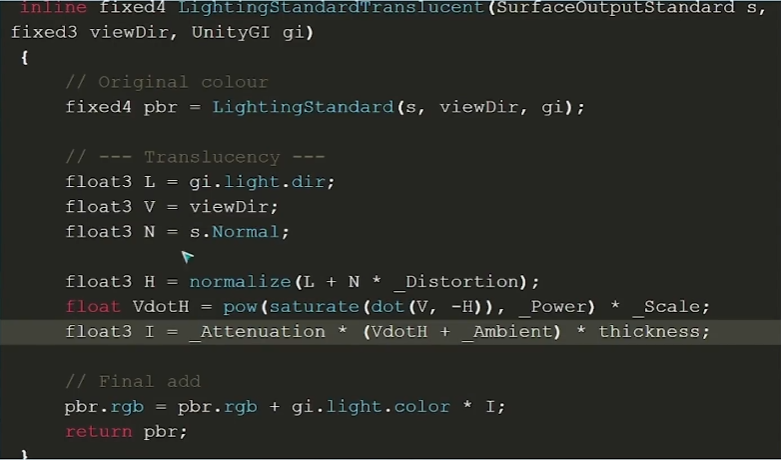 ## 三、参考 **参考资料:** [图形 5.5水体渲染.note (youdao.com)](https://note.youdao.com/ynoteshare/index.html?id=cc4438d7cf28de227151bfe1a7fd1ca9&type=note&_time=1727400224760 "图形 5.5水体渲染.note (youdao.com)") [真实感水体渲染技术总结 - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/95917609 "真实感水体渲染技术总结 - 知乎 (zhihu.com)") [Chapter 2. Rendering Water Caustics \| NVIDIA Developer](https://developer.nvidia.com/gpugems/gpugems/part-i-natural-effects/chapter-2-rendering-water-caustics "Chapter 2. Rendering Water Caustics | NVIDIA Developer") [Shader相册第6期 --- 实时水面模拟与渲染(一) - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/31670275 "Shader相册第6期 --- 实时水面模拟与渲染(一) - 知乎 (zhihu.com)") [【学习笔记】Unity 基于GPU FFT海洋的实现-实践篇 - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/96811613 "【学习笔记】Unity 基于GPU FFT海洋的实现-实践篇 - 知乎 (zhihu.com)") http://dljz.nicethemes.cn/news/show-321967.html [虚幻4渲染编程(环境模拟篇)【第七卷:海洋模拟-上-海洋模拟理论推导】 - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/60374372 "虚幻4渲染编程(环境模拟篇)【第七卷:海洋模拟-上-海洋模拟理论推导】 - 知乎 (zhihu.com)") [虚幻4渲染编程(环境模拟篇)【第八卷:海洋模拟-中-在UE中实现FFT海洋】 - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/67481306 "虚幻4渲染编程(环境模拟篇)【第八卷:海洋模拟-中-在UE中实现FFT海洋】 - 知乎 (zhihu.com)") [9.1 xorshift算法-CSDN博客](https://blog.csdn.net/m0_66201040/article/details/123953110 "9.1 xorshift算法-CSDN博客") [fft海面模拟(一) - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/64414956 "fft海面模拟(一) - 知乎 (zhihu.com)") [fft海面模拟(二) - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/64726720 "fft海面模拟(二) - 知乎 (zhihu.com)")