图论day61:最小生成树|最小生成树理论基础:prim算法、kruskal算法(思维导图版)、53.寻宝(卡码网 第七期模拟笔试)
-
- 最小生成树理论基础(思维导图版)
- [53.寻宝(卡码网 第七期模拟笔试)](#53.寻宝(卡码网 第七期模拟笔试))
最小生成树理论基础(思维导图版)

53.寻宝(卡码网 第七期模拟笔试)
题目描述
在世界的某个区域,有一些分散的神秘岛屿,每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路,方便运输。
不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将 所有岛屿联通起来(注意:这是一个无向图)。
给定一张地图,其中包括了所有的岛屿,以及它们之间的距离。以最小化公路建设长度,确保可以链接到所有岛屿。
输入描述
第一行包含两个整数V 和 E,V代表顶点数,E代表边数 。顶点编号是从1到V。例如:V=2,一个有两个顶点,分别是1和2。
接下来共有 E 行,每行三个整数 v1,v2 和 val,v1 和 v2 为边的起点和终点,val代表边的权值。
输出描述
输出联通所有岛屿的最小路径总距离
输入示例
7 11
1 2 1
1 3 1
1 5 2
2 6 1
2 4 2
2 3 2
3 4 1
4 5 1
5 6 2
5 7 1
6 7 1输出示例
6提示信息
数据范围:
2 <= V <= 10000;
1 <= E <= 100000;
0 <= val <= 10000;
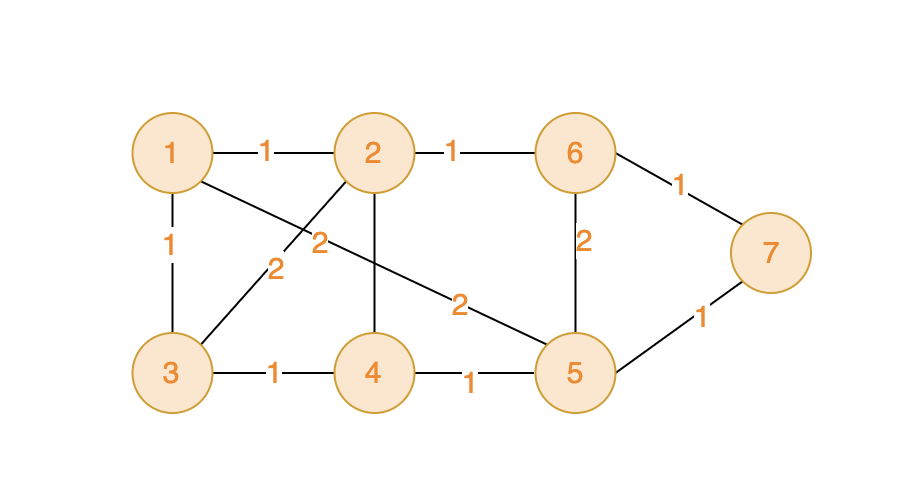
如下图,可见将所有的顶点都访问一遍,总距离最低是6.
1.prim法
cpp
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main()
{
int v,e,x,y,k;
cin>>v>>e;
vector<vector<int>> grid(v+1,vector<int>(v+1,10001));
for(int i=0;i<e;i++)
{
cin>>x>>y>>k;
grid[x][y]=k;
grid[y][x]=k;
}
vector<int> minDist(v+1,10001);
vector<bool> isInTree(v+1,false);
for(int i=1;i<=v;i++)
{
int cur=-1;
int minVal=INT_MAX;
for(int j=1;j<=v;j++)
if(!isInTree[j]&&minDist[j]<minVal)
{
minVal=minDist[j];
cur=j;
}
isInTree[cur]=true;
for(int j=1;j<=v;j++)
if(!isInTree[j]&&grid[cur][j]<minDist[j])
minDist[j]=grid[cur][j];
}
int result=0;
for(int i=2;i<=v;i++)
result+=minDist[i];
cout<<result<<endl;
}2.kruskal法
cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct Edge
{
int l,r,val;
};
int n;
vector<int> father(10001,0);
void init()
{
for(int i=1;i<=n;i++)
father[i]=i;
}
int find(int u)
{
return u==father[u]?u:father[u]=find(father[u]);
}
void join(int u,int v)
{
u=find(u);
v=find(v);
if(u==v)
return;
else
father[v]=u;
}
bool cmp(Edge& edge1,Edge& edge2)
{
return edge1.val<edge2.val;
}
int main()
{
int e,v1,v2,val;
cin>>n>>e;
vector<Edge> edges;
for(int i=1;i<=e;i++)
{
cin>>v1>>v2>>val;
edges.push_back({v1,v2,val});
}
sort(edges.begin(),edges.end(),cmp);
init();
int result=0;
for(int i=0;i<e;i++)
{
int x=find(edges[i].l);
int y=find(edges[i].r);
if(x!=y)
{
result+=edges[i].val;
join(x,y);
}
}
cout<<result<<endl;
}分析思路:
