数据结构与算法分析：你真的理解图算法吗——深度优先搜索（代码详解+万字长文）

一、前言

图是计算机科学中用来表示复杂结构信息的一种基本结构。本章我们会讨论一些通用的围表示法,以及一些频繁使用的图算法。本质上来说,一个图包含一个元素集合(也就是顶点),以及元素两两之间的关系(也就是边),由于应用范围所限,本章我们仅仅讨论简单图,简单围并不会如(a)那样有一个顶点的一条边是自己指向自己,以及不会如(b)那样一对顶点之间存在多条边。

一个图G=(V.E)由一个顶点集V以及一个边集E组成,算法中通常会出现如下几种图:
无向图

顶点(u,v)之间的关系模型不需要考虑关系的方向如何。在处理对称信息时,这种图非常有用。例如,汽车可以在A镇和B镇之间的路上双向行驶。
有向图

顶点(u,v)之间的关系和顶点(vu)之间的关系不同,后者或许不存在。例如,一个提供驾驶信息的程序必须存储单线道路的信息,以避免给出错误的方向。
有权图

顶点(u,v)之间的关系是有权重的,可以是数值的也可以是非数值的。例如,在A镇和B镇之间的道路有公里数,当然也包含了等袋时间这个信息。
超图

在顶点(w,v)之间可能存在多种关系,本章我们将讨论限定在简单图上。

如果图中任意两点之间都存在一条边,那么这个围是连通图。一个有向有权图的定义为:一个非空顶点集合( V n V_n Vn... V n − 1 V_{n-1} Vn−1）一个有向的边集合,每对顶点之间只有一条边,以及每条边上都有一个正权值。在很多应用中,这个权值被认为是距离或者开销。对某些应用来说,我们希望能够放宽权值必须为正的限制(例如,负值可以反映利润情

况),但是我们必须高度关注这样做的后果。考虑下图的有向有权图,它由6个顶点4条边组成。存储这个图有两个标准的数据结构:它们都显式地存储了权值,隐式表示了边的方向。

一种数据结构叫邻接表,如下图所示：

下图则是表明了如何用一个内阶的邻接知阵来存健有向有权图,每个维度可以被索引。条目A[i][j]存储的是从 V i V_{i} Vi到 V j V_{j} Vj的边的权值,当A[i][j]=0时,顶点,和頂点v,之间不存在边。使用邻接知阵表示法,在加一条边只要要常数时间。

我们他可以使用邻接表和邻接矩阵来存储无向图。看看下图6-5的无向图,我们使用< v 0 , v_{0}, v0, v 1 , v_{1}, v1,...... v k − 1 v_{k-1} vk−1>来描述一条有k个顶点的路,这条路遍历了k<1条边,一个有向图的路径是由同一方向的边组成。在下图中,路径< v 0 , v_{0}, v0, v 1 , v_{1}, v1, v 3 , v_{3}, v3, v 4 , v_{4}, v4,>是有效的。环是一个多次包含了同一个顶点的路径。一个环通常用其最小形式表示,在下图中,在路径< v 0 , v_{0}, v0, v 1 , v_{1}, v1, v 3 , v_{3}, v3, v 4 , v_{4}, v4, v 2 , v_{2}, v2, v 1 , v_{1}, v1, v 3 , v_{3}, v3, v 4 , v_{4}, v4, v 2 , v_{2}, v2,>中存在一个环,这个环可以用 v 1 , v_{1}, v1, v 3 , v_{3}, v3, v 4 , v_{4}, v4, v 2 , v_{2}, v2, v 1 v_{1} v1来表示。注意上上上个图的有向有权图权图,存在一个环< v 3 , v_{3}, v3, v 3 , v_{3}, v3, v 3 , v_{3}, v3,>.

存储问题

当使用部接表来存储无向图时,同一条边(w,v)在邻接表中出现了两次,一次是在的邻接节点健表,一次是在v的邻接节点键表。因此,相比同样数目的顶点和边的有向图,无向图在邻接表中存储所需要的存储空间是前者的两倍,当使用邻核知阵来存储无向图时,你必须保证条目A[AU)=AU114,不需要任何的额外存储空间。

当使用二维矩阵来表示元素集合中内个元素的潜在关系时,需要注意一些事项。首先,矩阵需要 n 2 n^2 n2个元素的存储空间，即使有时候元素之间的关系集合非常小。在这些情况下,也就是所谓的稀疏围,由于计算机内存的限制,不可能存储超过数千个顶点的图。例如,Java虚拟机使用默认值256MB,创建一个二维的int[4096][4096]矩阵就已经超出可用内存。即使程序员能够在一台有着更多内存的计算机上执行程序,事实上创建的矩阵规模存在一个固定的上界,另外,在大规模矩阵中存储稀疏键图,遍历矩阵来寻找边的操作的开销会很大，并且这种存储方法也限制了更多的改进。第二,当顶点之间有多种关系时,不适合使用矩阵,为了能够在矩阵中存储这种关系,矩阵中每一个元素将会当作一个表。

每一种邻接表示法都存储了相同的信息,假设,你写了一个程序,需要计算出世界上任意两个城市之间的最便宜的航班。每条边的权重和两个城市之间最便宜直航的价格有关(假设载线不会中转),根据2005年国际机场协会(ACI)发布的一份接告,世界上有总共1659个机场,这样也就需要一个有2752281个条目的二维矩阵。那么就有一个问题:"多少条目是有值的",它的答案率决于直航航线的数目,ACI的接告也显示,2005年有71600000次 "航空括动", 简单地说每天有大概196164次航班。即使所有的航班都是在两个不同机场之间的直航(虽然直航的数目要比这个小很多),这个矩阵也有93%是空值 ------一个非常好的稀疏矩阵的例子!当使用一个邻接表表示无向图时,我们可以使用一些方法来减少需要的存储空间,假设一个顶点的部接顶点为:2.8.1.5.3.10.11和4,首先,这些部接顶点会以升序来存储,这样做能修快速地定位是否存在一条边(w.y),在这种结构下,虽然有8个邻接顶点，但是确定是否边（u，6）是否存在只需要6次比较。当然，添加一条边就不再是常数时间，这里我们需要权衡一下利弊。其次，为了能够更加高效的检查是否边（u，v）存在，邻接表可以存储邻接顶点的范围，例子中的邻接表中八个顶点可以减少到三个；1-5、8、10-11。这种方法也能够减少是否存在一条边的计算次数，不过这会降低添加或者删除边的效率。
图分析

当使用本章的算法时,决定使用邻接表还是邻接矩阵的最重要因素是围是否为稀疏图。算法的性能是和围的顶点教IVIRRERRERR相关书一样,我们简化了性能的公式,无论在最好、最坏还是平均情况下,我们都使用V,E的大0记法来表示性能。

O(V)表示需要和图中的顶点数成直接比例的计算步数,但是图中边的密度他必须考虑,在稀疏图中,O(E)近似等于O(V),然而在稠密图中,它近似等于O( V 2 V^2 V2)。

我们将会看到,根据图的结构,一些算法会有两个变种,并且这两个变种的性能不尽相同,一个变种也许执行时间为O((V+E)*logV）,而另外一个是O( V 2 + E V^2+E V2+E)。哪个更加高效呢?下表告诉我们这个答案取决于图G是稀疏图还是橋稠密图。对于稀疏图来说， O ( ( V + E ) ∗ l o g V ) \mathrm{O}((V{+}E)^{*}\mathrm{log}V) O((V+E)∗logV)虽然更加高效一点，而对于稠密图, O ( V 2 + E ) O(V^2+E) O(V2+E)就更加快速了,标记为"均衡图"的条目，这种图的期望性能在稀疏图和稠密图上都是相同的，为 O ( V 2 ) O(V^2) O(V2),在这些图上，边的数目大致等于 O （ V 2 / l o g V ） O（V^2/log V） O（V2/logV）。

问题

使用图结构可以解决很多问题。本章我们只是讨论其中一些,不过你仍然有机会寻找到一些我们没有讨论的问题,然后去研究,给定一个用边来定义的图,很多问题会和图中两顶点之间的最短路径相关，路的长度就是路上边的长度之和。在"单源最短路径"这个问题上,给定一个顶点,我们需要计算出到图中其他所有顶点的最短路径。在"对顶点间最短路径"问题中,我们需要计算图中所有的顶点对(w.v)之间的最短路径。有些问题则是在更加深人地使用了图的结构,我们可以从一个图中构造出一个最小生成树(MST)。最小生成树是一个无向有权图,是原图边的一个子集,但是,原图的顶点仍然是连通的,而边的权值总和最小,在"最小生成树算法"一节,我们将会描述如何高效地解决这个问题。

我们首先从如何探索图开始讨论。两个最常使用的搜索方法是深度优先搜索(DFS)和广度优先搜索(BFS)。

二、算法描述

考虑下图左边的迷宫，在经过一尝试后，一个孩子能够快速地找到从起点s到终点t的路，但是计算机解决这个问题看起来就比较复杂，一种方法是假设离目标并不太远，然后做尽可能多的深度移动，也就是说，只要可以，随机选择一个方向，然后向这个方向前进，标记一下起点，如果你走上一条死路，或者不能在不重新访问顶点的情况下做任何深度移动，那么就会遇到另一条未访问的分支上，并且向这个方向前进。下图右边的数字表示的是一个解的分支点。事实上，在这个解中，我们访问了迷中的所有点。

我们能够用一个包含了点和边的图来表示上图的迷宫。一个顶点表示迷宫中的每一个分支点（在上图的右边用数字标记） ，当然也包括"末路点"。如果迷宫中在两个顶点之间存在一条有向路，并且在这个方向上没有其他的选择，那么我们就说存在一条边。从上图得到的迷宫的无向图表示如下图所示，每一个顶点都有一个唯一标识符。

为了解决这个问题，我们需要知道在图 G=（V，E）的顶点s到顶点r是否存在一条路。本例中，所有的边都是无向的，但是即使在迷宫上加一些限制条件，我们也能够非常容易地将其看成有向图。下图的详解包括了用伪代码描述的深度优先搜索。深度优先搜索的核心是递归的 dfs_visit（u）操作，这个操作访问之前没有访问过的顶点u。并且这个操作通过对顶点染色记录下了搜索进程。顶点可能会染成如下三种颜色；
白色

顶点还未访问。
灰色

顶点已经被访向过了，但是其可能还有没有被访问过的顶点。
黑色

顶点以及其所有的邻接顶点都已经被访向过了。

首先，所有的顶点初始为白色，然后深度优先搜索在源顶点 s 上调用 dfs_visit，在对 u 所有的未访向邻接顶点（它们为白色）递归调用 dfs_visit 之前，dfs_visit（u）将 u 染成灰色。一旦这些递归调用完成，那么我们将 u 染成黑色，然后函数返回。当递归函数 dfs_visit 返回，深度优先搜索开始回溯，直到回溯到一个有邻接顶点未被访问过的顶点（事实上，回溯到标记为灰色的顶点）。

对有向和无向图来说，深度优先搜索从 s 开始，访问了图中所有 s 可达的顶点。如果 G 中仍然有未访问，但是从s不可达的顶点存在，深度优先搜索将会随机从其中选择一个作为源点，然后重复操作。这个过程将会一直重复，直到 G 中所有的顶点都被访问。

在这个执行过程中，深度优先搜索遍历图中的边，计算和复杂的图结构有关的信息。深度优先搜索维护一个计数器，在一个顶点第一次被访问（标记为灰色）和完成在这个顶点上的深度优先搜索（标记为黑色）时，这个计数器增加计数。对于每个顶点，深度优先搜索记录如下信息。

pred[v]

前驱顶点，用来恢复从源点 s 到顶点 v 的路。

discovered[v]

其值为当深度优先搜索第一次访向 v 时，计数器增加后的值，简写为 d[v]。

finished[v]

其值为完成在这个顶点 v 上的深度优先搜索，计数器增加后的值，简写为 f[v]。

顶点访问的顺序将会改变计数器的值。所以需要注意邻接节点的顺序。对很多构建在深度优先搜索上的算法，深度优先搜索计算出来的信息都是非常有用的，包括拓扑排序，寻找强连通部，寻找网络中潜在的弱点。让我们来看看上图，假设顶点的邻接顶点是升序排列。那么计算出来的信息如下图所示。当计数器为 18，顶点 8 正在被访问时，让我们看看图中顶点的颜色。图中有些部分（例如标记为黑色的点）已经被完全搜索井且不会被重复访问。我们需要注意白色顶点的 d 都将大于 18（因为它们现在还没有被访间），以及黑色顶点的f都小于等于 18，因为它们已经被完全搜索过，灰色顶点的 d 小于等于 18，f 大于 18，因为它们现在正处于某条递归访问的路上。

深度优先搜索没有对图的一个整体认识，所以它是盲目地搜索顶点<5，6，7，8>，即使是南辕北辙。一旦深度优先搜索结束，pred[]的值能够用来生成一条从任意顶点到源点 s 的路。当然，这条路也许不会是最短路径，例如<s，1，3，4，5，9，>，但是最短的路径是<s， 6， 5，9， > （这里的最短路径指的是s到r经过的点的个数最少） 。

深度优先搜索计算三个数组。d[v]表示的是 v 第一次被访问时，计数器的值。pred[v]是深度优先搜索时，顶点 v 的先驱顶点。[fv]则是当 v 被完全访问过之后，计数器的值，即 dfs_visit（v）之后计数器的值。如果原图是不连通的，那么根据 pred[]的值实际上可以得到一个由深度优先树组成的深度优先森林。对于森林中的树来说，它们根节点的 pred[r]的值都为-1。此算法对于有向图和无向图同样适用。

深度优先搜索（DFS）的基本过程：

深度优先搜索（DFS）

算法步骤：

1. 初始化：

   • 创建一个栈（可以使用递归实现）来存储待访问的节点。
   • 创建一个布尔数组 visited，用于标记每个节点是否已访问。

2. 遍历：

   • 从起始节点开始，将其推入栈并标记为已访问。
   • 当栈不为空时，执行以下操作：
     • 从栈中弹出一个节点 u。
     • 访问节点 u，进行必要的处理（如打印或存储）。
     • 遍历 u 的所有邻接节点 v：
       • 如果节点 v 未被访问，则将其推入栈并标记为已访问。

三、复杂度分析

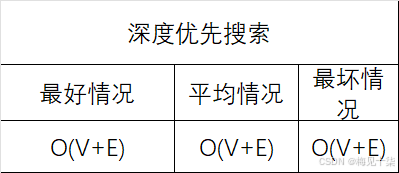
深度优先搜索只需要在遍历图时存储每个顶点的频色（白、灰或者黑）。因此深度优先搜索在逾历围时，只需要很小的存储开销。深度优先搜索能够在数组中存储其遍历图时的信息。事实上，深度优先搜索对图的唯一要求是能够遍历给定顶点的所有邻接顶点，于是这样，我们能够在复杂的数据结构上方便地进行深度优先搜索。因为 df_visit 函数将原图看做一个只读结构。但是，深度优先搜索仅仅依靠当前的信息，是一种盲目的搜索，它并没有一个明智的计划来快速达到目标顶点 t。

图中的每一个顶点都会调用递归的dfs_visit函数一次。dfs_search中的循环不会执行超过n次。在dfs_visit函数中,每一个邻接顶点都要被检查,对于有向围来说,每一条边都只会遍历一次,然而在无向图中,它们会被遍历一次然后会被检查一次,在任何情况下,性能开销都是O(V+E)。

四、适用情况

以下是一些常见的适用场景：
图的遍历：

DFS 可以用于遍历图中的所有节点，适合于寻找所有连通分量。
路径查找：

在寻找从一个节点到另一个节点的路径时，DFS 可以有效地探索所有可能的路径，特别是在解决迷宫问题时。
拓扑排序：

在有向无环图（DAG）中，DFS 可以用于拓扑排序，帮助确定任务的优先级或依赖关系。
解决约束满足问题：

如数独、八皇后问题等，DFS 可以通过递归尝试所有可能的放置方式，寻找有效解。
生成组合和排列：

在生成集合的所有组合或排列时，DFS 是一个有效的选择。
强连通分量：

在有向图中，DFS 可以用于查找强连通分量，通过 Tarjan 或 Kosaraju 算法实现。
解决游戏问题：

在一些回合制游戏中（如棋类游戏），DFS 可以用于评估所有可能的游戏状态，帮助选择最佳策略。
图的颜色问题：

在一些图的颜色问题中，DFS 可以用于验证图是否可着色或寻找可行的着色方案。
寻找特定节点：

当需要寻找特定特征的节点时，DFS 可以在较深的层次上更早找到目标。
注意事项：

空间复杂度：DFS 在深度较大的图中可能会导致栈溢出，因此在处理非常深的树或图时，要考虑使用迭代的方式或增加栈的大小。

性能：在某些情况下（如图较大且稀疏时），DFS 可能不是最优选择，这时广度优先搜索（BFS）或其他算法可能更合适。

五、算法实现

下面是深度优先搜索的C++实现：

#include <iostream>
#include <vector>
#include <list>

using namespace std;

// 定义边的类型枚举
enum edgeType { Tree, Backward, Forward, Cross };

// 定义顶点颜色枚举
enum class vertexColor { white, gray, black };

// 定义边标签结构
struct EdgeLabel {
    int u, v;
    edgeType type;
    EdgeLabel(int _u, int _v, edgeType _type) : u(_u), v(_v), type(_type) {}
};

// 定义图的类型（使用邻接表表示）
class Graph {
public:
    vector<vector<int>> adj;
    Graph(int n) : adj(n) {}

    void addEdge(int u, int v) {
        adj[u].push_back(v);
    }

    const vector<int>& operator[](int u) const {
        return adj[u];
    }

    auto begin(int u) const {
        return adj[u].begin();
    }

    auto end(int u) const {
        return adj[u].end();
    }
};

void dfs_visit(Graph const& graph, int u, vector<int>& d, vector<int>& f, vector<int>& pred, vector<vertexColor>& color, int& ctr, list<EdgeLabel>& labels);

// 访问顶点 u 并更新信息
void dfs_visit(Graph const& graph, int u, vector<int>& d, vector<int>& f, vector<int>& pred, vector<vertexColor>& color, int& ctr, list<EdgeLabel>& labels)
{
    color[u] = vertexColor::gray; // 将顶点 u 标记为灰色（正在访问）
    d[u] = ++ctr; // 记录发现时间

    for (int v : graph[u]) {
        if (color[v] == vertexColor::white) { // 如果顶点 v 仍然是白色（未访问）
            pred[v] = u; // 更新前驱
            dfs_visit(graph, v, d, f, pred, color, ctr, labels); // 递归访问 v
        }
    }

    color[u] = vertexColor::black; // 将顶点 u 标记为黑色（完成访问）
    f[u] = ++ctr; // 记录完成时间

    // 处理所有邻接顶点
    for (auto ci = graph.begin(u); ci != graph.end(u); ++ci) {
        int v = *ci;
        edgeType type = Cross; // 初始化边的类型为交叉边
        if (color[v] == vertexColor::white) {
            type = Tree; // 如果 v 是白色，则为树边
        }
        else if (color[v] == vertexColor::gray) {
            type = Backward; // 如果 v 是灰色，则为回边
        }
        else {
            if (d[u] < d[v]) {
                type = Forward; // 如果 d[u] < d[v]，则为前向边
            }
        }
        labels.push_back(EdgeLabel(u, v, type)); // 添加边标签
    }
}

// 从顶点 s 开始执行深度优先搜索
void dfs_search(Graph const& graph, int n, vector<int>& d, vector<int>& f, vector<int>& pred, vector<vertexColor>& color, list<EdgeLabel>& labels) {
    int ctr = 0; // 发现和完成时间的计数器
    for (int u = 0; u < n; u++) {
        if (color[u] == vertexColor::white) { // 如果顶点 u 是白色
            dfs_visit(graph, u, d, f, pred, color, ctr, labels); // 开始访问
        }
    }
}

int main() {
    // 创建一个包含 5 个顶点的图
    Graph graph(5);
    graph.addEdge(0, 1);
    graph.addEdge(0, 2);
    graph.addEdge(1, 3);
    graph.addEdge(1, 4);
    graph.addEdge(2, 4);

    int n = 5; // 顶点数量
    vector<int> d(n, 0); // 发现时间
    vector<int> f(n, 0); // 完成时间
    vector<int> pred(n, -1); // 前驱
    vector<vertexColor> color(n, vertexColor::white); // 顶点颜色
    list<EdgeLabel> labels; // 边标签

    // 从顶点 0 开始深度优先搜索
    dfs_search(graph, n, d, f, pred, color, labels);

    // 输出发现和完成时间
    cout << "顶点\t发现时间\t完成时间\n";
    for (int i = 0; i < n; i++) {
        cout << i << "\t" << d[i] << "\t\t" << f[i] << "\n";
    }

    // 输出边标签
    cout << "\n边标签:\n";
    for (const auto& label : labels) {
        cout << "(" << label.u << ", " << label.v << ") : " << static_cast<int>(label.type) << "\n";
    }

    return 0;
}

下面是两个不同写法的dfs_visit函数的对比：

void dfs_visit(int u, int& time, vector<int>& d, vector<int>& f, vector<int>& color, vector<vector<int>>& G) {
    color[u] = 1;
    d[u] = ++time;
    for (int v : G[u]) {
        if (color[v] == 0) {
            dfs_visit(v, time, d, f, color, G);
        }
    }
    color[u] = 2;
    f[u] = ++time;
}
/*
这两个 dfs_visit 函数在功能上都是执行深度优先搜索（DFS），但实现上有一些明显的差异。以下是对比和说明：

1. 参数类型和数量
上段代码中的 dfs_visit:

接受的参数有多个，包括图的结构、前驱节点数组、颜色数组、时间计数器、边标签列表等。
使用的颜色类型是枚举 vertexColor，用来表示未访问、正在访问和已完成。
新代码中的 dfs_visit:

参数较少，主要是顶点 u、时间 time、发现时间数组 d、完成时间数组 f、颜色数组 color 和图 G。
颜色使用整数（0, 1, 2）来表示状态，分别对应未访问、正在访问和已完成。
2. 颜色管理
上段代码:
使用 vertexColor 枚举来表示顶点的状态，赋值 gray 表示正在访问，赋值 black 表示已完成。
新代码:
使用简单的整数来表示状态，color[u] = 1 代表正在访问，color[u] = 2 代表已完成。
3. 边标签处理
上段代码:

在遍历邻接点时，记录边的类型（树边、回边、前向边、交叉边），并将这些信息存储在边标签列表中。
新代码:

没有处理边标签，专注于顶点的发现和完成时间。
4. 递归调用
上段代码:

在递归调用 dfs_visit 之前更新前驱节点数组 pred。
新代码:

没有更新前驱节点的信息，这可能影响对DFS树的重建或后续操作。
5. 代码风格
上段代码:
使用更丰富的结构体和类型定义，增加了代码的可读性和维护性。
新代码:
相对简单直接，适合快速实现DFS，但可能在后续分析中缺少某些信息。
总结
这两个函数的主要目的是相同的，都是实现深度优先搜索。上段代码提供了更多的功能和信息处理（如前驱记录和边标签），而新代码则相对简单，适用于基本的DFS实现。如果你的目标是构建DFS树或分析图的结构，上段代码可能更适合；如果只需要基本的DFS遍历，新代码足够用。
*/

如果d[]和f[]不需要,那么这些值的计算过程(以及将其作为函数参数)可以从上例中的代码删除掉。深度优先搜索可以得到关于图中边的额外信息。尤其在深度优先森林中,有四种边。
树边

对于所有pred[v]-u的顶点v,dfs_visit(u)坊问边(w.v)来遍历图。这些边记录了深度优先搜索的进程。上图中的边(s,1)就是一个很好的例子。
后边

当dfs_visit(u)处理到顶点时,如果v是的邻接顶点并且是灰色,那么深度优先搜索就会知道它已经访问过这个顶点。图6-10中的边(8.3)就是一个很好的例子。
前边

当dfs_visit(u)处理到顶点的,如果v是的部接顶点,v的颜色是黑色,而且&在v之前被访问,那么边(w,v)是一个前边。那么深度优先搜索就会知道它已经访问过这个顶点了。图6-10中的边(5,9)就是一个很好的例子。
交叉边

当dfs_visit(u)处理到顶点时,如果的邻接顶色是黑色,而且色是黑色,而且在v之后被访问,那么边(u,v)是一个交叉边。交叉边只是在有向图中存在。标记这些边的代码在上例中。对于无向图,边(w.v)可能会被标记很多次,但是一般来说,只有在这条边第一次被标记时其标记有效。

六、算法优化

以下是一些常见的优化策略：
剪枝：

在搜索过程中，如果发现某个路径不可能满足目标条件，可以提前结束该路径的搜索，从而减少不必要的计算。
使用迭代加深：

结合深度优先搜索和广度优先搜索的优点，通过在一定深度限制内进行多次深度优先搜索，可以在不消耗太多内存的情况下找到最优解。
路径存储：

对已访问的节点进行标记，避免重复访问，从而减少时间复杂度。使用集合或哈希表来存储已访问节点，可以快速检查节点是否已经被访问。
深度限制：

对于某些问题，可以设置最大深度限制，防止在深度过大的情况下出现栈溢出，尤其是在递归实现中。
调整搜索顺序：

根据启发式信息调整子节点的访问顺序，可以更快地找到目标节点。例如，优先搜索可能更有希望的路径。
记忆化搜索：

将中间结果缓存起来，避免重复计算同样的子问题，提高效率。
图的表示：

选择合适的数据结构表示图（如邻接表或邻接矩阵）可以提高DFS的性能，尤其是在稀疏或密集图中。

七、引用及参考文献

1.《算法设计手册》