一、说明
二项分布描述了在固定数量的独立伯努利试验中一定数量的成功的概率,其中每个试验只有两种可能的结果(通常标记为成功和失败)。
二、探讨伯努利模型
例如,假设您正在抛一枚公平的硬币 (其中正面成功,反面失败) 五次。每次翻转都是一次独立的伯努利试验,成功概率(正面朝上)为 0.5。现在,您有兴趣找到从 5 次翻转中正好获得 3 次正面的概率。此方案适合二项分布,因为您有固定数量的试验(五次翻转),并且每个试验只有两种可能的结果(正面或反面),因此它们成为独立的伯努利试验。
总而言之,伯努利是:
- 描述固定数量的独立伯努利试验的成功次数。
- 由两个参数定义:试验次数 n 和成功概率 p。
二项式分布的概率质量函数 (PMF) 由以下公式给出:
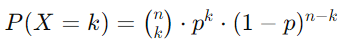
此处里:

现在,让我们分解公式:

三、二项式分布的期望值和方差
期望,通常称为均值或平均值,表示随机变量在重复实验中的理论平均结果。在二项分布的上下文中,期望 E[X] 表示在给定数量的试验中预期的平均成功次数。二项分布的期望公式为:
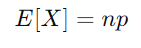
其中 n 是试验数,p 是单次试验成功的概率。
假设您抛硬币 10 次。每次抛硬币都是一个独立的伯努利试验 ,其中正面朝上**(成功)** 的概率为 p = 0.5,反**面(失败)**的概率相同 q = 1−p = 0.5
现在,让我们使用公式 E[X] = np 计算预期的正面 E [X] 数量:
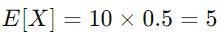
这个结果告诉我们,平均而言,我们期望在 10 次抛硬币中得到 5 次正面。
另一方面,方差衡量分布围绕其平均值的散布或离散度。在二项分布中,方差 Var[X] 量化了实际结果与预期成功数的偏差程度。二项分布方差的公式为:
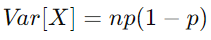
该公式反映了这样一个事实,即二项式分布中结果的分布受试验数 n 和成功概率 p 的影响。较高的试验次数或接近 0.5 的成功概率往往会导致较大的方差,这表明成功次数的变异性更大。
四、示例:计算机失败的概率
假设一家工厂有一台机器在任何一天都有 5% 的几率出现故障。我们想要找到机器在 30 天内 恰好失败 3 次的概率。在这里,每天代表一个独立的伯努利试验,有两种可能的结果:机器失败(成功)或不失败(失败)。
鉴于:
- n=30(试验次数或天数)
- p=0.05(机器在任何给定日期出现故障的概率)
我们可以使用二项分布来查找 30 天内恰好失败 3 次的 概率。二项分布的概率质量函数 (PMF) 由下式给出:
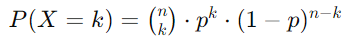
将给定的值代入公式:
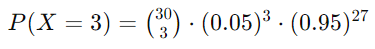
这里:

计算这些值:
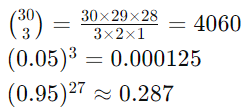
因此:
P (X=3) = 4060 × 0.000125 × 0.287 ≈ 0.145
因此,机器在 30 天内恰好失败 3 次的概率约为 0.145,即 14.5%。
五、用于轧制模具 100 次的二项式 PMF
在这个例子中,我们探讨了将公平的六面骰子滚动 100 次的二项式概率质量函数 (PMF)。我们感兴趣的是确定在这 100 次掷骰子中掷出特定数字(例如,掷出"1"或"6")一定次数的概率。由于骰子的每一面都有相等的概率为 1/6,因此特定数字出现的次数分布遵循二项式分布。
二项分布由试验数 n 和成功概率 p 来表征。这里,n = 100 和 p = 1/6 。该图显示了 k 获得 k 次成功(滚动特定数字)的概率,范围从 0 到 100。
为了进一步分析分布,我们在图上计算并显示预期的成功数 (期望) 和分布的可变性 (方差)。
bb
import matplotlib.pyplot as plt
from scipy.stats import binom
# Number of trials (number of dice rolls)
n = 100
# Probability of success (rolling a specific number, e.g., 1 or 6)
p = 1 / 6
# Create a range of possible number of successes (0 to n)
k = range(n + 1)
# Calculate the PMF for each number of successes
pmf_values = [binom.pmf(x, n, p) for x in k]
# Calculate expectation and variance
expectation = n * p
variance = n * p * (1 - p)
# Plotting the PMF
plt.figure(figsize=(8, 5))
plt.bar(k, pmf_values, width=1.0, edgecolor='black')
plt.title('Binomial PMF for Rolling a Die 100 Times (Rolling a Specific Number)')
plt.xlabel('Number of Successes (Rolling a Specific Number)')
plt.ylabel('Probability')
plt.grid(True)
# Show expectation and variance on the plot
plt.axvline(expectation, color='r', linestyle='dashed', linewidth=2.5, label=f'Expectation (mean): {expectation:.2f}')
plt.axvline(expectation - variance**0.5, color='orange', linestyle='dashed', linewidth=2.5, label=f'Standard Deviation: {variance**0.5:.2f}')
plt.axvline(expectation + variance**0.5, color='orange', linestyle='dashed', linewidth=2.5)
plt.legend()
plt.show()这是上述代码的输出:
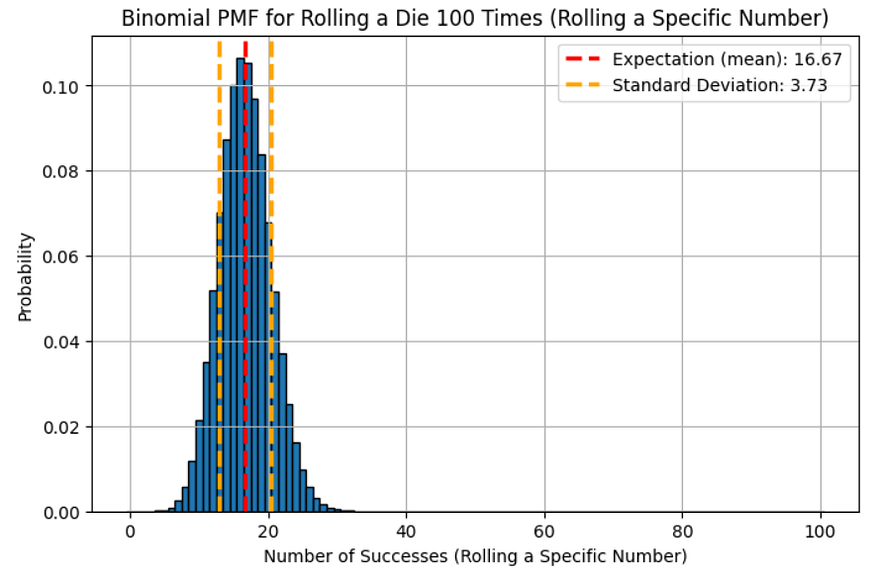
期望值和方差计算:
- 期望值(平均值):E[X] = np = 100 × 1/6 ≈ 33.33
- 方差:Var[X] = np(1−p) = 100 × 1/6 × 5/6 ≈ 27.78 ≈ 27.78
- 标准差:Var[X] ≈ 5.27
六、变化 (p) 对掷模二项分布的影响
二项分布中的概率 p 表示每个试验中特定结果的可能性。当掷一个公平的骰子时,对于骰子的任何特定面,p 通常为 1/6。通过改变 p,我们可以探索如果骰子有偏差,分布如何变化。例如,如果加载骰子以将特定数字滚动到 0.3 的概率,则二项分布的形状和分布将发生变化,与公平骰子相比,在平均值附近显示更高的成功集中度。
简单地说,我们可以更改上面的代码来计算和绘制不同 p 值的 PMF:
bb
import matplotlib.pyplot as plt
from scipy.stats import binom
# Number of trials (number of dice rolls)
n = 100
# Define different probabilities of success
p_values = [1/6, 0.35]
# Create a range of possible number of successes (0 to n)
k = range(n + 1)
plt.figure(figsize=(8, 5))
for p in p_values:
# Calculate the PMF for each number of successes
pmf_values = [binom.pmf(x, n, p) for x in k]
# Calculate expectation and variance
expectation = n * p
variance = n * p * (1 - p)
# Plotting the PMF
plt.plot(k, pmf_values, label=f'p = {p}')
# Annotate the plot with expectation and variance
plt.axvline(expectation, color='r', linestyle='dashed', linewidth=1)
plt.axvline(expectation - variance**0.5, color='g', linestyle='dashed', linewidth=1)
plt.axvline(expectation + variance**0.5, color='g', linestyle='dashed', linewidth=1)
plt.title('Binomial PMF for Rolling a Die 200 Times with Varying p')
plt.xlabel('Number of Successes (Rolling a Specific Number)')
plt.ylabel('Probability')
plt.legend()
plt.grid(True)
plt.show()这是上述代码的输出:
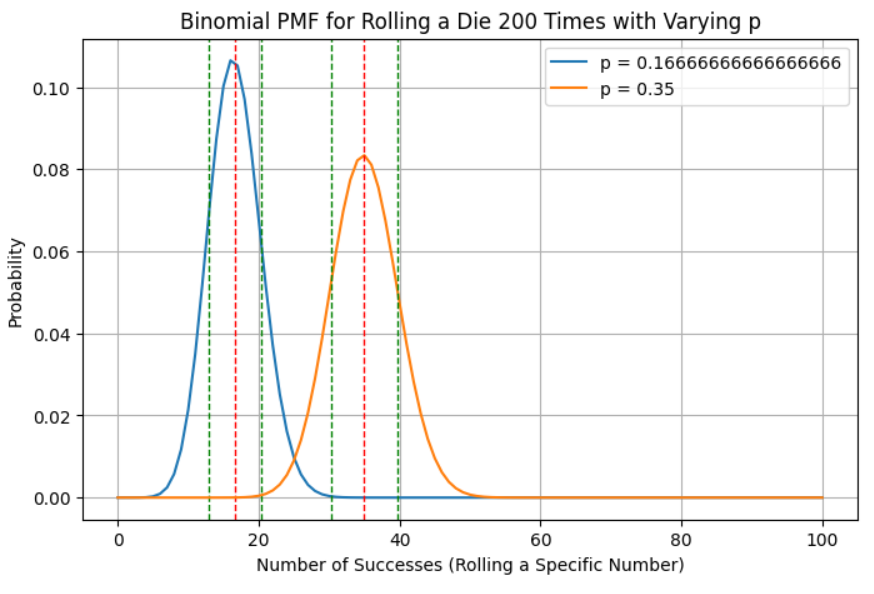
变化 p :该脚本计算并绘制两个不同 p 值的 PMF:1/6(公平骰子)和 0.35(偏置骰子)。
在机器学习系列的第 21 天,我们探索了二项分布,这是一种基本概率分布,用于对固定数量的独立伯努利试验的成功次数进行建模。